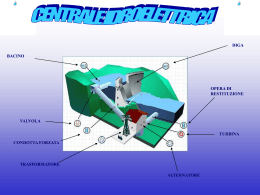
Progettazione di un impianto mini-idroelettrico; Studio della turbina Che cosa sono le turbine? A cosa servono? Le turbine sono macchine idrauliche che utilizzano direttamente lβenergia cinetica del fluido derivata indirettamente dal dislivello geodetico naturale o creato artificialmente che conferisce alla massa liquida una energia potenziale di posizione. Esse hanno quindi il compito di trasformare lβenergia cinetica dellβacqua in energia meccanica che sarà poi trasformata in energia elettrica da un alternatore. : o Potenza o Rendimento o Numero di giri caratteristico ο La potenza La potenza disponibile in una macchina idraulica viene calcolata mediante la seguente formula: ππ = πΎππ» (πππ/π ) ο Il rendimento Il rendimento di una macchina idraulica è dato dalla moltiplicazione dei vari rendimenti della macchina (idraulico, volumetrico, meccanico) ed è dato dalla formula: π = ππ β ππ£ β ππ ο Il numero di giri caratteristico Il numero di giri caratteristico è un parametro che fornisce le condizioni di similitudine di funzionamento per due macchine dello stesso tipo ma di dimensionamento diverso. Esso è dato dalla seguente formula: ππ = π π 5 π»4 Tipo di turbina Pelton Francis Numero di giri caratteristico nc Dislivello H (m) 1 getto 17 - 30 2 getti 17 - 42 4 getti 24 - 60 Lenta 60 - 100 400 - 240 normale 100 - 200 240 - 90 veloce 200 - 300 300 - 400 90 - 50 50 - 40 400 - 600 30 - 18 600 - 800 18 - 10 800 - 1000 10 - 5 Turbine a elica e Kaplan 300 - 2000 La ruota Pelton o Le turbine PELTON sfruttano salti elevati e portate dβacqua anche piccole; orientativamente H=300 β 2000m e Q< 20m³/s La girante: è formata da una serie di palettature a doppio cucchiaio, ogni pala è dotata di un coltello centrale che ha il compito di dividere il getto in due correnti che lambiscono le superfici interne della pala. Il distributore: chiamato spina double è formato da spina a sezione variabile sistemata nel centro dellβugello. La girante La spina double Turbina Francis Caratteristiche fondamentali o la turbina Francis è una turbina a reazione o è impiegata per salti medi e bassi e portate più elevate della Pelton o il distributore circonda la girante ed è formato da palette inclinabili assialmente collegate fra loro in modo da poterle comandare con un unico comando e in maniera sincronizzata. Il distributore Turbina Kaplan Caratteristiche fondamentali o turbina a reazione o utilizzata per bassi salti e portate elevate o numero di giri caratteristico molto alto o metodo di regolazione analogo alla Francis però nelle Kaplan si possono inclinare anche le palette della girante così da avere una regolazione più ampia. Il distributore Dimensionamento della turbina ο Premessa: Al momento della scelta della turbina abbiamo optato per una Kaplan ad asse verticale dal momento che abbiamo disponibile un salto utile (distanza dal pelo libero dellβacqua allβasse della turbina) molto basso, dettato dal fatto che il nostro progetto è realizzato per un impianto miniidroelettrico; di conseguenza avremo anche una portata limitata e molto variabile, dal momento che è caratteristica nota dei torrenti presenti sul nostro territorio. Parametri scelti: π Numero di giri della turbina n: 250 [ ] 1β² π³ Portata massima πΈπππ : 2[ ] π π³ Portata media πΈπππ : 1,5[ ] π Salto utile h: 3,7 [m] Grafico delle portate annuali portata Q 2000 1800 1600 1400 1200 1000 800 600 400 200 0 portata Q ο Calcolo il numero tipico di macchina (K), calcolato per la portata massima 1 πΎπππ₯ = π β ππππ₯ 2 3 (πβ)4 1 22 = 26,18 β (9,81 β 3 3,7)4 = 2,5 Per trovare il numero tipico di macchina devo prima calcolare lβΟ π= 2ππ 2π250 πππ = = 26,18 60 60 π ο Scelgo il numero di Thoma dal diagramma della figura 1 Fig.1 Numero di Thoma per le turbine Francis, Elica e Kaplan Nel nostro caso il numero di Thoma ππͺ = 0,44 ο Ricavato il numero di Thoma procedo al calcolo dellβaltezza allo scarico π§2 = ππ΅ β ππ£ β β ππ = 0 ππ Lβaltezza allo scarico risulta 0 dal momento che la pressione allo scarico (ππ΅ ) è uguale alla pressione dopo lo scarico (ππ£ ) ο Calcolo la portata di progetto πΈπ ricavando dalla tab.2 la relazione ππ = ππ π³ β ππππ₯ = 0,72 β 2 = 1,44 ππππ₯ π ππ ππππ₯ ο Avendo ora πΈπ ricalcolo K πΎπππ₯ = π β 1 ππππ₯ 2 3 (πβ)4 = 26,18 β 1 1,442 (9,81 β 3 3,7)4 = 2,12 ο Dalla tabella 2 ricavo Ο e Ο che saranno rispettivamente 0,23 e 0,22. ο Calcolo la velocità periferica della girante (Ue) π’π = πβ = π 9,81 β 3,7 π = 12,56 0,23 π ο Trovo ora il diametro esterno De π·π = 2π’π 2 β 12,56 = = 0,96 π π 26,18 ο Calcolo il diametro interno della girante (Di) π·π = π·π 2 β 4π = πππ’π 0,962 β 4 β 1,44 = 0,5 π π β 0,22 β 12,56 ο Calcolo la velocità dellβacqua (Ca) ππ = π β π’π = 0,22 β 12,56 = 2,763 π π ο Attribuisco un valore al rendimento idraulico:( πΌππ = π, ππ) e calcolo lβaltezza teorica (ht) βπ‘ = β β πππ = 3,7 β 0,91 = 3,37 π ο Pongo πππ = π quindi π«ππ = πππ ππ’π = ππ’1 = Ξππ’ = βπ‘ β π 3,7 β 9,81 π = = 2,63 π’π 12,56 π ο Trovo lβinclinazione della paletta ( π·β ) π½β = ππππ‘ππ ππ 2,763 = ππππ‘ππ = 14° ππ’1 + ππ’2 2,63 + 0 π’π β 12,56 β 2 2 ο Calcolo la velocità indisturbata della corrente relativa (πβ ) πβ = ππ 2,763 π = = 11,42 π πππ½β π ππ14 π ο Ricavo il rapporto tra il passo e la corda (t/l) dalla tabella 3 e il numero di palette (ππ ) dalla tabella 2. Tab.3 Valori ottimali del rapporto t/l Nel nostro caso t/l risulterà 0,74 e il numero di palette sarà 7. ο Calcolo il passo (t) e della corda (l) π‘= ππ·π π β 0,96 = = 0,43 π π§π 7 π= π‘ 0,43 = = 0,58 π 0,74 0,74 ο Secondo i profili NACA 6410 calcolo: ο Lβangolo di inclinazione del profilo esterno della paletta dove lβacqua entra (π½π1 ) ο Lβangolo di inclinazione del profilo esterno della paletta allβuscita dellβacqua (π½π2 ) π½π1 = 14 + 1,54 = 15,54° π½π2 = 14 β 1,60 = 12,40° I restanti dati riguardanti il calcolo dei profili nelle varie sezioni della paletta sono stati realizzati con excel allo scopo di facilitare le operazioni di calcolo. Qui di seguito la tabella con i vari risultati D Ο ht 0,50 26,18 3,37 0,60 0,70 0,80 0,90 0,96 g 9,81 cu1 ca u 5,05 2,763 6,55 4,21 7,85 3,61 9,16 3,16 10,47 2,81 11,78 2,63 12,57 t 0,22 0,27 0,31 0,36 0,40 0,43 l 0,30 0,36 0,42 0,49 0,55 0,58 π½β 34,51 25,67 20,58 17,26 14,91 13,80 π½π1 61,60 37,17 26,45 20,69 17,11 15,54 π½π2 22,89 19,38 16,78 14,78 13,20 12,40 Conclusioni e ringraziamenti La difficoltà principale incontrata in questa area di progetto è stata il reperimento di un libro dove fosse descritto il dimensionamento della turbina Kaplan, dal momento che la maggioranza dei libri in commercio non lo tratta o ne parla in maniera superficiale, approfondendo di più le turbine Pelton e Francis. Il materiale è stato reperito in internet e su libri di testo. Il progetto mi è servito per capire lβimportanza dellβ idroelettrico sul nostro territorio, il quale non è, come dimostrato, sfruttato come si dovrebbe dal momento che ci sono innumerevoli siti adatti a questo tipo di energia rinnovabile non sfruttati. Vorrei ringraziare soprattutto il prof. Pesavento Fabio che mi ha aiutato nel capire il procedimento per il dimensionamento della turbina ed è sempre stato molto disponibile. I miei ringraziamenti vanno anche a tutti i docenti della nostra classe che sono sempre stati disponibili per qualsiasi chiarimento ed aiuto.
Scarica
