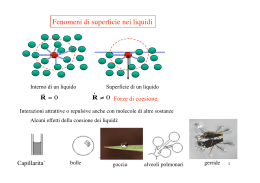
1
La lezione di oggi
Le interazioni tra molecole alla superficie di un liquido
generano fenomeni come:
• tensione superficiale
• capillarità
In medicina:
Equilibrio alveolare
2

La tensione superficiale

La legge di Laplace

La capillarità

Equilibrio alveolare
3
Osservazione sperimentale
Un insetto cammina sull’acqua
come se se la superficie fosse un sottile foglio di gomma
4
Bolle di sapone
5
Goccia di liquido
OSSERVAZIONE
Le gocce sono sferiche
 Molecole
 Forze attrattive tra
molecole
 All’interno: risultante delle
forze = 0
 Equilibrio
6
Goccia di liquido
Molecola vicino alla superficie
• Forza risultante diversa da 0
• Tende a spingerla all’interno della
goccia
• Devo compiere lavoro per andare
verso la superficie
• Energia del fluido aumenta per ogni
molecola spostata verso la superficie
La sfera è la configurazione
ad energia minima
7
In natura, le configurazioni ad
energia minima sono favorite
Una goccia deformata
…
… tende a ritornare sferica
 La forza peso dell’insetto tende a fare
aumentare la superficie dell’acqua
 Le forze di tensione superficiale si
oppongono
8
Tensione superficiale (t ):
definizione operativa
“fil di ferro”

τ
Forza applicata

τ
Vista da sopra
Vista laterale

τ

τ
sottile pellicola di liquido
 F tende ad aumentare la superficie di
liquido
 t si oppone
 Ho 2 superfici in gioco
9
Tensione superficiale







La F è applicata al fil di ferro
Risultato: la superficie del liquido aumenta
Porto verso la superficie di interfaccia un certo numero di molecole che
erano all’interno della pellicola
La forza data dalla tensione superficiale (t) si oppone
Devo compiere un lavoro
Il lavoro (L) è proporzionale all’aumento di superficie (DS)
L
Definisco, operativamente: τ 
DS
 Sposto la barretta di un tratto x
 Ottengo una DS = l. x
 Compio un lavoro L = F. x
 Attenzione:

le superfici sono 2 (vedi prima) !!!
Fx F
τ

2l  x 2l
10
Tensione superficiale
di alcune sostanze
Sostanza
Tensione
superficiale
(N.m-1)
Mercurio (20oC)
0.44
Sangue intero
(37oC)
0.058
Plasma (37oC)
0.073
Acqua (0oC)
0.076
Acqua (20oC)
0.072
(100oC)
0.059
Acqua

t si misura in N.m-1
L
τ
DS
L  τ  ΔS

F
τ
2l
F  2l  τ
Se t è grande devo:
 Compiere L grande
 Applicare F grande
11
La legge di Laplace
Domanda:
quali forze agiscono su una goccia ?
 Differenza di pressione (interno/esterno)
 Tensione superficiale del fluido
Fpressione
 Considero mezza goccia
 Pressione: vettori F perpendicolari alla superficie
sferica
 Tensione superficiale: vettori lungo la circonferenza
Ftensione superficiale
y
12
La legge di Laplace
Fpressione  A  DP  π R 2 DP
Fpressione
All’equilibrio:
Fpressione  Ftens.sup
Ftens.sup.  2 π R τ
π R 2 DP  2π R τ
Ftens. superficiale
y
2τ
PL 
R
Legge di Laplace per
una goccia sferica
4τ
PL 
R
Legge di Laplace per
una bolla sferica
τ
PL 
R
Legge di Laplace per
un tubo cilindrico
13
La tensione di vapore


Liquido in equilibrio con il suo vapore (stato aeriforme intermedio
tra liquido e gas)
 tensione di vapore

Nota: Pressione di vapore = Tensione di vapore

Pressione necessaria a impedire ad altro liquido di evaporare

Goccia di liquido in equilibrio con il suo vapore:
 DP = tensione di vapore
14
Esercizio
Qual è il raggio della più piccola goccia sferica di acqua che si può formare
senza evaporare (confrontare: tensione di vapore) ?
Condizioni a
contorno
2τ
PL 
R
tacqua = 7.2.10-2 N.m-1
Tensione di vapore = 2.33.103 Pa
2  (7.2  10 -2 N  m -1 )
-5
R

6.2

10
m  62 μm
3
2.33  10 Pa
15

La tensione superficiale

La legge di Laplace

La capillarità

Equilibrio alveolare
16
Il fenomeno della capillarità
q
Sperimentalmente osservo:
• Acqua “sale” in un tubo di vetro
menisco
(“bagna il vetro”)
q
• Mercurio “scende” in un tubo di vetro
(“non bagna il vetro”)
q
• Forza di coesione:
forze tra molecole dello stesso tipo
q
• Forze di adesione:
forze tra molecole di tipo diverso
• Acqua + Vetro: Adesione > Coesione
• Mercurio + Vetro: Adesione < Coesione
17
Il fenomeno della capillarità
q < 90o
q > 90o
18
Il fenomeno della capillarità
Visto dall’alto.
l vale 2pr
F
q
F
F
F
τ
l
Fcapillarita  2 π r τ cosθ
19
Il fenomeno della capillarità
Fcapillarita deve bilanciare il peso del liquido sollevato
w  mg 
 ρVg 
 ρ(πr h)g
2
20
La legge di Jurin
Fcapillarita  2 π r τ cosθ
w  ρ(πr 2 h)g
2 τ cosθ
h
ρ rg
ρ(π r h)g  2 π r τ cosθ
2
Altezza della colonna di liquido, fino al
menisco (superficie curva)
Con q = 90o  h = 0
h
Con q > 90o  h < 0
Con q < 90o  h > 0
21
Esercizio
n. 7.3, pag. 162 Borsa-Scannicchio
A quale altezza arriverà il menisco dell’acqua a 20 oC in un tubo
di raggio pari a 0.5 mm se esso è fatto di vetro (1) oppure di
paraffina (2) ?
tacqua = 0.072 N.m-1
qacqua-vetro = 25o
qacqua-paraffina = 107o
?
?
22
Esercizio
n. 7.3, pag. 162 Borsa-Scannicchio
A quale altezza arriverà il menisco dell’acqua a 20 oC in un tubo di raggio pari a 0.5 mm
se esso è fatto di vetro (1) oppure di paraffina (2) ?
tacqua = 0.072 N.m-1
qacqua-vetro = 25o
qacqua-paraffina = 107o
2 τ cosθ
h
ρ rg
2  0.072  cos25o
-2
h1  3

2.7

10
m  2.7 cm
3
o
10  0.5 10  9.8
2  0.072  cos107
-3
h2  3

8.7

10
m  - 8.7 mm
3
10  0.5  10  9.8
23

La tensione superficiale

La legge di Laplace

La capillarità

Equilibrio alveolare
24
L’esperienza del palloncino
Rorecchio< Rcorpo
Porecchio > Pcorpo
25
Equilibrio alveolare
Modello fisico degli alveoli polmonari
Sfere cave collegate da sottili condotti
Doppio strato
Interno: acqua (vapore saturo)
Esterno: strato elastico




Se avessi solo
lo strato di acqua
1
2
Legge di Laplace per
una bolla sferica
4τ
PL 
R
R2 < R1
PL2 > PL1
1 aumenta di volume a spese di 2
 Se fosse così, gli alveoli piccoli collasserebbero
 Nella realtà:


Elasticità tessuto
t del liquido che li bagna aumenta al diminuire di R
26
Riassumendo
I fenomeni molecolari danno
effetti macroscopici
quando considero le interfacce tra
elementi diversi
In medicina,
vi sono moltissimi casi
di questo genere
(tra gli altri, l’embolia e
gli alveoli polmonari)
Prossima lezione:
27