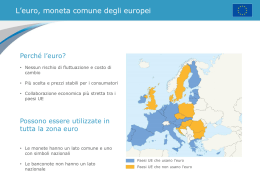
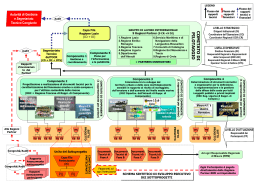
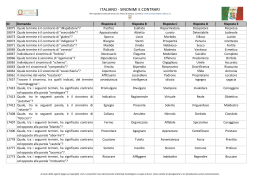
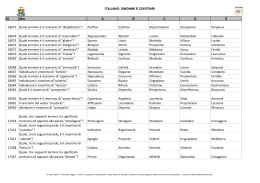
σ2 = <(x-m)2> =
= <x2 -2mx
+ m 2>
= <x2> -2m<x> + m2
= <x2>- 2m2+m2=
= <x2>- m2=
= <x2>- <x>2
= <(x-m) (x-m)>
La deviazione standard e’ la media dei quadrati
meno il quadrato della media
x
y
y
x
PijP=ij =
P P(x
(xi ,i,y
yjj))
dP= dxdy p(x,y)
in generale
in generale
Scriviamo > . P(A,B) = P(A)* P(B)*>F(A,B) =
dove F(A,B) = P(A,B)/(P(A)*P(B)) e poi
Pij
=
<
Pi= Σj Pij
Pi Pj
p(x,y)
= p(x) (p(y)
<
p(x)=∫dyp(x,y)
=PP(A)*F(A,B)
= P(B)*F(A,B)
p(y)=∫
dxp(x,y)
j= Σi Pij
<x> =
ΣiΣj xiPij ==
<y> =
ΣiΣj yjPij =
Σ=i Σi xiPi
=Σi yjPj
σx 2 =
<y>
<x> =
<y>
= =
∫dx∫dy xp(x,y)
∫dx∫dyxp(x,y) ∫dy∫dxyp(x,y)
∫dx x p(x)
= ∫dx x p(x) = ∫dy y p(y)
σx 2 =
σy 2 =
σx 2 =
σy 2 =
2
<(x-<x>)2> = <(y-<y>)2>= <(x-<x>)2> = <(y-<y>) > =
Σi (xi-<x>)2Pi Σj(yj-<y>)2Pj ∫dx(x-<x>)2p(x)∫dy(y-<y>)2p(y)
σxy = covarianza di x e y =
F(A,B) = 1
(y-<y>)>
=
<(x-<x>)
< x y > - <x> <y>)> =
ΣiΣj (xi-<x>) (yj-<y>) Pij
∫∫dxdy (x-<x>) (y-<y>)p(x,y)
Varianze e Covarianza
σx2 = = <(x-<x>) (x-<x>)>
= <x2>- <x>2
= <(x-<x>)2> =
σy2 = = <(y-<y>) (y-<y>)>
= <y2>- <y>2
= <(y-<y>)2> =
σxy = <(x-<x>) (y-<y>)>
= <x y> - <x><y>
La covarianza non deve essere positiva !!!
e’ positiva, se x e y si favoriscono
una fluttuazione di y-<y> con stesso segno
accompagna una di x-<x>
piu’ spesso che una con segno opposto
e’ nulla, se x e y sono indipendenti
una fluttuazione di y-<y> con stesso segno
accompagna una di x-<x>
altrettanto spesso che una con segno opposto
e’ negativa, se x e y si sfavoriscono
una fluttuazione di y-<y> con segno opposto
accompagna una di x-<x>
piu’ spesso che una con stesso segno