UNIVERSITA’ DEGLI STUDI DI PARMA FACOLTA’ DI ECONOMIA Corso di Corporate Banking a.a. 2009-2010 (Professor Eugenio Pavarani) Evoluzione della teoria del rischio finanziario da Markowitz al teorema della separazione e al CAPM 1 Le curve di indifferenza sulla frontiera di Markowitz • Markowitz ha mostrato l’esistenza della Frontiera Efficiente • Ma quale portafoglio sulla Frontiera è preferibile? • Dipende dall’avversione/propensione al rischio dell’investitore (la scelta è soggettiva, sulla base delle proprie curve di indifferenza) Spazio oltre-frontiera Portafogli oggettivamente dominanti E (R) Y X Portafogli dominati 2 Evoluzione della teoria del rischio finanziario Indice • La Capital Market Theory di Markowitz • Il Teorema della separazione di Tobin e la Capital Market Line • Il Capital Asset Pricing Model (CAPM) – Il rischio sistematico e il rischio diversificabile – L’intuizione di Sharpe e la Security Market Line 3 Investimento al tasso privo di rischio • Markowitz ha ragionato solo su titoli e portafogli rischiosi • Tobin ipotizza ora l’esistenza di titoli caratterizzati da rischio nullo ( = 0) che garantiscono quindi un rendimento sicuro. Questo tasso è il Risk Free Rate (Rf). • E’ ora possibile costruire ulteriori portafogli combinando quelli sulla frontiera efficiente (es. portafoglio A) con titoli privi di rischio (es. titolo B) ²p = a²∙²A+b²∙²B+2∙a∙b∙A∙B∙AB ²p = a²∙²A a = p / A E(Rp) = p / A ∙ E(RA) + (1- p / A ) ∙ Rf E(Rp) = Rf + [E(RA) – Rf] ∙ p/ A La frontiera efficiente è ora una spezzata costituita da portafogli con minor rischio a parità di rendimento 4 Il teorema della separazione di Tobin La nuova frontiera efficiente è una spezzata E (Rp) A’’ x’ Rf y A’ x A E(Rp) = Rf + [E(RA) – Rf] ∙ p A p 5 Il teorema della separazione di Tobin La nuova frontiera efficiente è una spezzata E (Rp) E (RA) A’’ x’ 1^ ipotesi: p = 0 Rf y 3^ ipotesi: 0 < p < A 2^ ipotesi: p = a * A p = A E(Rp) = Rf + [E(RA) – Rf] ∙ p A p p /A= a 6 Indebitamento al tasso privo di rischio • Abbiamo ipotizzato la possibilità di investire al tasso privo di rischio • Si ipotizza ora la possibilità di indebitarsi al tasso privo di rischio • Un investitore propenso al rischio può indebitarsi al tasso Risk Free, e investire al rendimento offerto dal portafoglio di mercato (= effetto di leva finanziaria maggior rendimento e maggior rischio) • Tale possibilità sposta ulteriormente la frontiera efficiente che diventa una semiretta 7 La nuova frontiera efficiente: una semiretta E(Rx) = (50 * 0,20) + (50 * 0,10) = 15% pA = 50% * A y’ E (R) y A x’ Rf E(RA) = 100 * 0,20 = 20% pA = 100% * A E(Ry) = (200 * 0,20) – (100 * 0,10) = 30% py = 200% * A 8 La Capital Market Line R(p) = Rf + E (R) R(m) - Rf (m) (p) CML Pendenza CML R(m) Rf m Rf = Risk Free Rate R(m)= rendimento atteso del portafoglio di mercato (m) p (m)= sqm del portafoglio di mercato 9 Il portafoglio di mercato • Il portafoglio m, detto Portafoglio di Mercato, è oggettivamente il migliore portafoglio di soli titoli rischiosi e domina qualsiasi altro portafoglio di soli titoli rischiosi. • La semiretta che congiunge Rf e il portafoglio di mercato costitituisce la nuova frontiera efficiente ed è detta Capital Market Line (CML). • Ogni portafoglio presente sulla frontiera efficiente è formato da una quota del titolo privo di rischio e da una quota del portafoglio di mercato. • La scelta del portafoglio rischioso è oggettiva: non dipende dalla propensione al rischio dell’investitore. • La quota di portafoglio rischioso da detenere è soggettiva: dipende dalla propensione al rischio del singolo investitore. i due momenti decisionali sono “separati” 10 Il prezzo di mercato del rischio • La pendenza della CML è il prezzo di mercato del rischio • esprime il premio di rendimento pagato dal mercato per ogni unità di rischio aggiuntiva • il rendimento di un portafoglio efficiente è determinato dall’equazione della CML R(p) = Rf + R(m) - Rf (m) (p) 11 Il teorema della separazione di Tobin • L’introduzione del tasso privo di rischio e la nuova frontiera efficiente (CML) separano: – l’individuazione del portafoglio rischioso ottimo: è una scelta oggettiva indipendente dalla propensione al rischio – la scelta soggettiva di posizionamento lungo la CML, cioè la quantità di ricchezza da investire nel portafoglio ottimo e nel titolo con tasso privo di rischio (che dipende dalle curve di indifferenza) – ogni investitore razionale detiene il portafoglio di mercato per importi diversi – quindi la reale composizione del portafoglio di mercato rispecchia la composizione ottimale 12 Evoluzione della teoria del rischio finanziario Indice • La Capital Market Theory di Markowitz • Il Teorema della separazione di Tobin e la Capital Market Line • Il Capital Asset Pricing Model (CAPM) – Il rischio sistematico e il rischio diversificabile – L’intuizione di Sharpe e la Security Market Line 13 Diversificazione e valore • La diversificazione consente di ridurre il rischio di un portafoglio • Un portafoglio di n titoli ha – un rendimento pari alla media ponderata dei singoli rendimenti; – per contro, ha un rischio complessivo inferiore alla media ponderata dei rischi dei singoli titoli • In sostanza, è meno rischioso a parità di rendimento • Domanda: il valore del portafoglio è maggiore della somma ponderata dei valori dei singoli titoli ? LA RISPOSTA E’ : NO, NON HA UN VALORE MAGGIORE • Esempio: nei fondi comuni di investimento, il valore del fondo è dato dalla somma del valore dei titoli presenti nel fondo stesso • Il mercato non riconosce nessun premio alla diversificazione. Perché ? 14 Perchè non è prezzato il rischio diversificabile • Non c’è premio, da parte del mercato, per chi fa semplicemente scelte razionali; è invece penalizzato chi non segue la strada della razionalità • Il rischio che viene prezzato dal mercato è il contributo fornito dal singolo titolo al rischio ineliminabile del portafoglio di mercato • Chi preferisce tenersi anche il rischio diversificabile, non ottiene un rendimento corrispondente a quella componente del rischio • Come misurare la componente rilevante del rischio ? • Il 2 di un titolo è un indicatore inadatto poiché ingloba nella misura del rischio anche la componente eliminabile tramite la diversificazione • Ciò che conta è l’insieme delle covarianze ponderate del singolo titolo con tutti gli altri titoli presenti sul mercato • E’ quindi necessaria una nuova misura di rischio 15 Il Capital Asset Pricing Model • Come misurare il contributo di ogni singolo titolo al rischio complessivo del portafoglio di mercato? – solo questa componente di rischio è rilevante per determinare il rendimento del titolo – essendo eliminabile con la diversificazione la componente specifica, il mercato finanziario considera nella determinazione del rendimento atteso soltanto la componente non diversificabile 16 Evoluzione della teoria del rischio finanziario Indice • La Capital Market Theory di Markowitz • Il Teorema della Separazione di Tobin e la Capital Market Line • Il Capital Asset Pricing Model (CAPM) – Il rischio sistematico e il rischio diversificabile – L’intuizione di Sharpe e la Security Market Line 17 La varianza di un portafoglio di tre titoli : la matrice varianza-covarianza ²P = a²∙²A+b²∙²B+ c²∙²C + 2∙a∙b∙AB+2∙a∙c∙AC+2∙b∙c∙BC A A a²∙²A B b∙a∙BA C c∙a∙CA B a∙b∙AB b²∙²B c∙b∙CB C a∙c∙AC b∙c∙AC c²∙²C a = peso del titolo A nel portafoglio b = peso del titolo B nel portafoglio c = peso del titolo C nel portafoglio 18 Ipotizziamo che il portafoglio di mercato sia composto da 8 titoli Matrice Varianze-Covarianze portafoglio di mercato con 8 titoli. A B C D E F G H A B C covarianze tra i singoli titoli D E F G H Varianze dei singoli titoli 19 Aggiungendo il titolo I al portafoglio… Il contributo del nuovo titolo alla varianza del portafoglio di mercato è dato soprattutto dalle covarianze con gli altri titoli. A B C D E F G H I A B C D E F G La varianza del titolo I incide sul rischio del portafoglio soltanto per 1 / 81 = 1 / N*N se i titoli hanno tutti lo stesso peso H I 20 Il contributo del singolo titolo al rischio del portafoglio di mercato • Il contributo di un titolo alla varianza del portafoglio è dato soprattutto dalla somma ponderata delle covarianze del titolo con gli altri titoli sul mercato • La varianza del titolo è una componente minima • All’aumentare del numero di titoli sul mercato il contributo della sola varianza diventa sempre più piccolo ed irrilevante: in tal modo viene realizzata la diversificazione 21 Il rischio sistematico e il rischio diversificabile • Il rischio di un qualsiasi portafoglio può essere distinto in due componenti – rischio non sistematico (o diversificabile) – rischio sistematico • Rischio non sistematico: deriva da fattori legati alla società emittente il titolo. E’ eliminabile con la diversificazione. • Rischio sistematico: è legato a fattori macroeconomici, è ineliminabile e corrisponde al rischio del portafoglio di mercato. 22 La riduzione della varianza di un portafoglio con la diversificazione Rischio non sistematico Rischio sistematico n 23 Evoluzione della teoria del rischio finanziario Indice • La Capital Market Theory di Markowitz • Il Teorema della separazione di Tobin e la Capital Market Line • Il Capital Asset Pricing Model (CAPM) – Il rischio sistematico e il rischio diversificabile – L’intuizione di Sharpe e la Security Market Line 24 La Security Market Line È possibile dimostrare che il rendimento atteso di un titolo i è pari a E[R(i)] = Rf + [ R(m) – Rf] (i, m) / 2 (m) Rapporto tra il rischio rilevante del singolo titolo e il rischio del portafoglio di mercato Es: se i valori sono uguali, il rapporto è = 1 il titolo ha stesso rischio e stesso rendimento del portafoglio di mercato > 1 più elevato rendimento atteso < 1 più basso rendimento atteso 25 La Security Market Line È possibile dimostrare che il rendimento atteso di un titolo i è pari a E[R(i)] = Rf + [ R(m) – Rf] (i, m) / 2 (m) E[R(i)] = Rf + [ R(m) – Rf] i • La SML consente di stimare il rendimento atteso di un titolo in funzione del suo contributo al rischio del portafoglio di mercato • Il contributo al rischio generale di portafoglio da parte del singolo titolo è misurato dall’indice Beta dato dal rapporto della covarianza tra titolo e mercato con la varianza del mercato i = (i, m) 2 (m) m= (m, m) 2 (m) =1 • Per visualizzare l’equazione che definisce il rapporto rischio rendimento per un singolo titolo occorre passare dal piano (R,) al piano (R,) 26 La Security Market Line SML E (Ri) es. 7,75% Alto rendimento R(m) Basso rendimento Rf E[R(i)] = Rf + i [ R(m) – Rf] m MRP Pendenza SML es. 4,75% Market risk Premium (MRP) es. 3,0% Basso rischio (m) = 1 Alto i rischio 27 L’indice Beta • La covarianza misura il legame tra i rendimenti del titolo e quelli del portafoglio di mercato • Il rappresenta la misura in cui, in media, i rendimenti di un titolo variano al variare dei rendimenti di mercato • Il del mercato è per definizione pari ad uno, poichè la covarianza tra il mercato e se stesso è pari alla varianza • Il del mercato è la media ponderata dei titoli presenti sul mercato dei diversi 28 Il Beta e il Market Risk Premium • Un titolo che fornisce un modesto contributo al rischio sistematico del mercato ha un inferiore ad 1 • Un titolo che fornisce un rilevante contributo al rischio sistematico del mercato ha un superiore ad 1 • Il MRP è il premio per il rischio del mercato, poiché indica quante unità di rendimento è possibile attendersi per avere assunto rischio nella misura = 1 • Uno studio di Banca d’Italia, ha stimato nel 5,69% il MRP sul mercato finanziario italiano 29 L’applicazione della SML la stima del costo del capitale azionario • Il rendimento atteso dall’azionista è il costo opportunità del capitale azionario per l’impresa • per non distruggere valore, l’impresa deve remunerare l’azionista in misura coerente con il rischio assunto e con il rendimento atteso Rendimento atteso dagli azionisti che hanno investito nel titolo i R(i) = Rf + i [ R(m) – Rf] Costo del capitale azionario 30
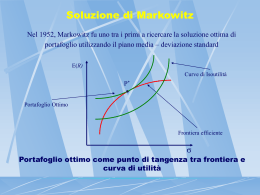
Scaricare