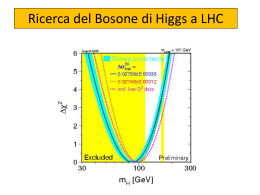
Introduzione
Il punto di partenza per la costruzione del Modello Standard e’ una Lagrangiana
di campi liberi o auto-interagenti che sia invariante sotto un dato gruppo di
simmetria globale
La Lagrangiana e’ invariante per trasformazioni del tipo:
U e’ una matrice simmetrica, T (hermitiani) sono i generatori del gruppo di
simmetria globale G.
Se G e’ un gruppo di tipo SU(N) allora avremo N2 -1 generatori hermitiani a
traccia nulla.
I termini di interazione ed i campi dei bosoni di gauge vengono introdotti rendendo
locale la simmetria del gruppo G:
U()  U( (x) ) = exp( ig T (x) )
La simmetria della Lagrangiana e’ preservata introducendo la derivata covariante,
cioe’ se effettuiamo la sostituzione:
E’ possibile introdurre un termine cinetico per i campi di gauge che risulta esserre del tipo
seguente:
L’espressione della Lagrangiana contenente icampi di materia e dei bosoni di
gauge sara’ quindi:
Alcune osservazioni di carattere generale:
Una Lagrangiana cosi’ scritta non puo’ contenere termini di massa nei campi
di gauge che violerebbero la simmetria di gauge!
Il termine FF prevede termini cubici e quartici di autointerazione dei
campi di gauge
In particolare nella costruzione del Modello Standard possiamo considerare i
gruppi di simmetria:
U(1)  1 geneartore (QED, )
SU(2)  3 generatori (settore elettrodebole, W,Z)
SU(3)  8 generatori (QCD, gluoni)
Se consideriamo il settore elettordebole del Modello Standard il gruppo di
simmetria G e’ dato da:
E’ possibile dare massa ai bosoni di gauge attraverso il meccanismo di
Higgs. Consideriamo un doppietto di campi:
Con Lagrangiana data da:
Il potenziale V e’ dato da:
La particolarita’ risiede nel valore di 2 come e’
evidente dalla forma del potenziale V.Tutti gli stati per i
quali si ha:
Sono di minimo per il potenziale V.
Una trasformazione di fase ( U(1) ) connette tutti gli stati di minimo per il potenziale
V.
Se scegliamo lo stato di minimo allora tale simmetria e’ rotta (spontaneous
symmetry breaking)!!
La lagrangiana globale conserva invece la sua simmetria di gauge!
In particolare e’ possibile scegliere una gauge in cui lo stato di vuoto sia dato da:
Il campo di Higgs potra’ scriversi come:
H(x) e’ un campo reale.
Il secondo grado di liberta’ e’ stato assorbito nella scelta della gauge.
Ricompare nelle trasformazioni dei campi di gauge.
Termini di potenziale
Sostituendo l’espressione del campo di Higgs in V() otteniamo:
Sono presenti:
1)
Termine di massa dell’Higgs 2v2
2)
Termini di autointerazione (H3 e H4)
Termini cinetici
Partendo dall’espressione seguente:
Svolgendo i calcoli si giunge alle seguenti conclusioni:
• I bosoni W e Z acquistano massa pari a:
Dalla misura della costante di Fermi GF si ottiene il valore di v:
Termini cinetici
L’accoppiamento tra i bosoni di gauge e l’Higgs e’ dato da:
E risulta essere proporzionale alle masse dei bosoni di gauge!
Termini di massa per i fermioni
Nella Lagrangiana del Modello Standard termine di massa dei fermioni
violerebbe la simmetria di gauge:
Il meccanismo di Higgs e’ utilizzato anche in questo caso introducendo un
accoppiamento alla Yukawa del tipo:
gf [ (LH)  R + h.c.]
Si ottiene che le masse dei fermioni mf= gf v/2 e quindi anche in questo
caso l’accoppiamento e’ proporzionale alle masse dei fermioni.
Regole di Feynman
Nel Modello Standard gli accoppiamenti dell’Higgs sono fissati, l’unico
parametro libero e’ la massa data da:
Limiti sulla massa del bosone di Higgs:
Considerazioni teoriche
Risolvendo l’equazione del gruppo di rinormalizzazione per la costante di
accoppiamento  presente nella Lagrangiana dell’Higgs si ottiene:
Limiti inferiori sulla massa del bosone
di Higgs:
Un limite inferiore puo’ essere ottenuto richiedendo che il potenziale
dell’Higgs sia limitato inferiormente. Questa richiesta e’ soddisfatta se
()0 nell’intervallo di energia in cui ritieniamo attendibile la teoria.
Limiti superiori sulla massa del bosone
di Higgs:
1) Un limite superiore si ottiene richiedendo che la teoria resti perturbativa e
quindi () 1 per tutti i valori di < ( scala della teoria)
Limiti superiori sulla massa del bosone
di Higgs:
Consideriamo inoltre lo scattering di bosoni Z poloarizzati longitudinalmente
Richiedendo che sia valido il limite di unitarieta’ dello sviluppo perturbativo
deve risultare che (ampiezza in onda S):
Tale “limite” diventa piu’ stringente se consideriamo anche lo scattering degli
altri bosoni (800 GeV).
Misure indirette
Alcune grandezze osservabili elettrodeboli sono sensibili a parametri quali mt e
mH. Misure di altissima precisione di queste osservabili consentono di inferire
informazioni su mt e mH anche senza una misura diretta!!
Ad esempio MW e’ dipendente mt e da mH tramite l’esistenza di diagrammi di
ordine superiore:
Utilizzando le misure di precisione (LEP) e’ interessante considerare il seguente
plot:
Misure indirette di mW and mt (linea continua)
Misure dirette of mW and mt (linea in verde)
mt = 178.0 4.39 GeV
mW = 80.425 0.034 GeV
Questi risultati sembrano indicare la presenza di un bosone di Higgs “leggero”
compatibile con quanto previsto dal Modello Standard
L’indicazione di un Higgs “leggero” diventa ancora piu’ forte se consideriamo i
risultati di un fit su tutti i parametri osservabili del Modello Standard nel settore
elettrodebole
114 GeV < mH < 251 GeV at the
95% of condence level.
• Collisioni p-p
• Frequenza di Bunch-crossing = 40 MHz
• Frequenza di Interazione ~109 Hz @ L = 1034 cm-2 s-1
• Eventi acquisiti 100 Hz (Fattore di reiezione 107)
Higgs 10-2 - 10-1 Hz
Top
tot = 80 mb
109 interazioni
al secondo!
W
10 Hz
2 Khz
Gluon Fusion
Vector Boson Fusion
Higgs Strahlung
ttH
• E’
dunque possibile considerare una grande varieta’ di
modalita’ di produzione e canali di decadimento per l’Higgs
• Tra questi, 2 canali di decadimento si caratterizzano
nell’ambito sperimentale del LHC come “favoriti” per
un’eventuale scoperta!
a) ggH 
MH<150 GeV
b) ggH ZZ*4leptoni
MH>130 GeV
• Caratterizzati da un BR molto basso
BR(H ZZ*4leptoni)0.12%
MH  500 GeV
• L’andamento di BR  costante per H  (0.06 pb) mentre
presenta una struttura piu’ complessa per H ZZ*4leptoni.
Fondo irriducibile proveniente dai processi
gg,qq .
Il segnale puo’ essere osservato sul fondo
continuo solo se la risoluzione
sperimentale su M e’ molto elevata (1%)
Fondo irriducibile proveniente dal
processo:
qq  ZZ*4leptoni
Fondi riducibili:
tt bbWW
(decadimento semileptonico del b)
Zbb