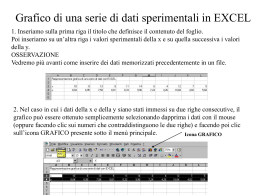
Interpolazione e regressione
• Molto
frequentemente
si
scopre
l’esistenza
di
una
relazione
sperimentale tra due (o più) variabili ed
è allora naturale la ricerca di una
espressione matematica di questa
relazione sotto forma di un’equazione
che leghi fra di loro le variabili in
questione.
Interpolazione e regressione
• Date due variabili X e Y costruiamo un
diagramma di dispersione con i loro valori.
• Se tutti i punti giacciono più o meno su una
retta, si dice che tra le variabili esiste una
relazione lineare.
Interpolazione e regressione
• Se i punti stanno su una curva, la relazione è
non lineare.
• Se non c’è relazione fra le variabili diciamo
che sono incorrelate:
Interpolazione e regressione
• Il problema generale di trovare l’equazione della curva
che più si avvicina ai punti sperimentali è detto
interpolazione.
• Uno degli scopi principali dell’interpolazione è quello di
stimare una delle variabili (la variabile dipendente) per
mezzo dell’altra (la variabile indipendente). Il
procedimento di stima è chiamato regressione.
• Se y deve essere stimata mediante x per mezzo di
qualche equazione, chiameremo l’equazione una
equazione di regressione di y in x e la corrispondente
curva la curva di regressione di y in x.
Interpolazione e regressione
• In generale esiste più di una sola curva di un
certo tipo che interpola l’insieme dei dati. Al
fine di evitare l’intervento della valutazione
personale nella costruzione di rette, parabole
o altre curve interpolatrici è necessario
mettersi d’accordo su una definizione della
“migliore retta interpolatrice”, “migliore
parabola interpolatrice”, e così via.
METODO DEI MINIMI
QUADRATI
METODO DEI MINIMI
QUADRATI
• Chiamiamo Dn la deviazione (o errore) fra il
valore Yn e il corrispondente valore della
curva (positiva o negativa).
• Una misura della “bontà dell’interpolazione” è
la somma
D12 + D22 …..+ Dn2
METODO DEI MINIMI
QUADRATI
• La curva avente la proprietà che
D12 + D22 …..+ Dn2
è minima è detta migliore interpolante o
retta/curva dei minimi quadrati.
METODO DEI MINIMI
QUADRATI
SYi = A N+ B SXi
SXiYi = A S Xi+ B SXi2
• La prima delle due equazioni si ottiene dalla
sommatoria di entrambi i membri di
Y=A+BX ,
la seconda moltiplicando i membri per X e poi
facendo la sommatoria.
ESEMPIO:
8
y = 0,6833x + 0,4698
7
6
5
4
3
2
1
0
0
2
4
6
8
10
Caso della parabola
y
Carta
semilogaritmica