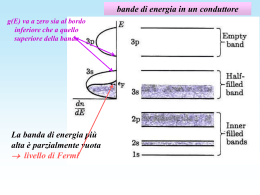
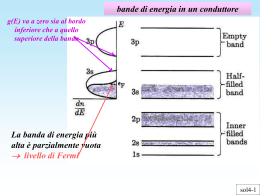
bande di energia in un conduttore
g(E) va a zero sia al bordo
inferiore che a quello
superiore della banda
La banda di energia più
alta è parzialmente vuota
 livello di Fermi
Overlap di bande di energia in un conduttore
bande di energia nel magnesio
bande di energia nel sodio
EF
la banda 3s è
parzialmente
vuota; l’overlap
con la banda 3p
estende la banda
permessa in cui
già cade EF
la banda 3s è totalmente
occupata, ma l’overlap con la
banda 3p fa sì che EF cada in
una zona di energie permesse
bande di energia in un isolante
EF
energy gap
bande di energia in
un semiconduttore
Energy gap
EF
diamante
5,3 eV
isolante
silicio
1,1 eV
semiconduttore
germanio
0,7 eV
semiconduttore
Modello classico: Drude e Lorentz, 1905
il problema: la legge di Ohm
V=RI
suggerisce una proporzionalità tra forza (campo
elettrico) e velocità (intensità di corrente)
moto “viscoso”
conduzione elettrica
nei metalli
l
I
V
il modello:
• gli elettroni in un conduttore si comportano come un “gas” di particelle
quasi libere che si muovono con velocità disordinata di agitazione
termica in tutte le direzioni, secondo la distribuzione di Boltzmann
(velocità termica vt )
• in presenza di un campo elettrico gli elettroni vengono accelerati in
direzione opposta al campo, acquistando una velocità media ordinata in
questa direzione (velocità di deriva vd )
• negli urti anelastici contro gli ioni del reticolo perdono l’energia in più
acquistata nell’accelerazione e ripartono con l’energia termica media
(il che spiega l’effetto Joule)
• la velocità media di deriva è quindi la velocità media acquistata sotto
l’azione del campo elettrico nel tempo medio  fra un urto e il successivo
(tempo di rilassamento)
S
legge di Ohm
resistività
V=RI


l 
l 
El   SJ ; El   SJ
S
S



2  
J  nevd  nea  ne
E
m
ne2
 

m
1
; 
quanto vale ?
m
l urti
vt
l
I
S
V
cammino libero medio
fra urti successivi
ne2

conduzione elettrica
nei metalli
; vt 
2 Et
3k BT

m
m
Nell’urto si ristabilisce l’equilibrio energetico, quindi in media l’elettrone cede
all’atomo l’energia acquistata a spese del campo elettrico (effetto Joule)

3mkBT
ne2l urti
inoltre:


e 
vd 
E  E
m
  ne
e

m
mobilità
2,5
spiega perché si genera il moto
viscoso e quindi la velocità limite
di deriva
• spiega perché la resistività
aumenta con la temperatura
• fornisce valori ragionevoli della
resistività a temperatura
ambiente
resistività 10^-8 ohm m
Il modello di Drude
secondo il modello
di Drude
2
1,5
1
0,5
0
-300
-200
-100
0
100
200
temperatura °C
Però ……
resistività 10^-8 ohm m
3,5
3
2,5
2
dati di misura
su campioni di
rame “puro”
1,5
1
0,5
0
0
50
100
temperatura °C
150
200
un calcolo di resistività secondo il modello di Drude
ipotizzando un libero
cammino medio
ragionevole: lurti  1 nm ;
n  1029 m-3



3mc2 k BT
ne 2l urti c
3  0,5 106 eV  0,03 eV
10 29 m 3e 1,6 1019 C 109 m  3 108 ms 1
0,2 103 eV
5 109 eCm1s 1
 4 108 VA 1m  4 10 8 m
Ciò che non funziona nel modello di Drude
resistività 10^-8 ohm m
2,5
• non riproduce la corretta dipendenza dalla
temperatura (ad alta temperatura è lineare in
T e non in  T)
dati di misura
su campioni di
rame “puro”
3,5
2,5
1,5
modello
di Drude
1
0,5
0
-300
-200
-100
0
100
200
temperatura °C
• non spiega l’effetto forte
della presenza di impurezze
(regola di Mathiessen)
Drude
2
1,5
1
0,5
estrapolazione
lineare
0
-0,5
-300
-250
-200
-150
-100 -50
0
temperatura °C
50
100
60
resistività del rame con
aggiunta di manganese
50
150
Ma soprattutto il modello di
Drude non è compatibile con il
comportamento quantistico
dell’elettrone nel solido
200
rho 10^-8 ohm m a 20°C
resistività 10^-8 ohm m
3
2
40
30
20
10
0
0
2
4
6
8
10
percentuale di Mn
12
14
16
il modello quantistico di Sommerfeld
L’elettrone è descritto da un “pacchetto di onde di Bloch” che si muove sotto
l’azione del campo elettrico esterno secondo l’equazione classica del moto:


dv d
m
 eE
dt


e 
E  E
che, risolta rispetto a vd, fornisce la soluzione: vd 
m
ottenuta con il modello di Drude.
È lecito il calcolo classico purché:
- si usi per m la “massa efficace”,
1
1 d 2E
 2
m  dk 2
- si verifichi che la larghezza del “pacchetto” in posizione e quantità di moto sia
 sufficientemente piccola, in modo che il moto possa essere trattato
classicamente nel tratto fra due collisioni successive,
 sufficientemente grande, in modo che le interazioni fra elettrone e reticolo
siano ben descritte dalla massa efficace
il modello quantistico di Sommerfeld
in assenza di campo elettrico esterno
in presenza di campo elettrico esterno
k
k
nello spazio k, la velocità di drift vd legata alla corrente elettrica genera
uno spostamento  k dell’intera distribuzione degli elettroni nel senso
contrario alla direzione del campo elettrico:
 m*v
e 
d
k 
 E


il modello quantistico di Sommerfeld
meccanismi di urto:
- riguardano solo gli elettroni vicino al
livello di Fermi, perché sono gli unici
ad avere disponibili livelli energetici
non occupati
- preferenzialmente lo scattering è
all’indietro dove ci sono più stati liberi a
energia minore
- l’urto non è contro gli ioni del reticolo,
perché la funzione d’onda di Bloch
tiene già conto del potenziale periodico
- gli urti possibili sono con ciò che non è
periodico:
- urti con le impurità
- urti con i fononi (vibrazioni reticolari)
collisioni nel modello quantistico
probabilità di collisione nell’unità di tempo:
1
1
vF
vF
Pcoll  Pimp  P fon 



 imp  fon limp l fon
cammino libero medio
per urti con le impurità
  imp   fon
velocità dell’elettrone di
energia prossima a quella
del livello di Fermi
cammino libero medio
per urti con i fononi
m*vF  1
1 
 2

ne  limp l fon 
(rispetto al calcolo di Drude, vF> vt però anche limp e lfon sono maggiori di lurti!)
collisioni con le impurezze
La probabilità di collisione con le impurezze, 1/limp
-è direttamente proporzionale alla densità di impurità, nimp , (la costante di
proporzionalità Simp è chiamata “sezione d’urto”):
limp
nim
1/l = S n
S
imp
imp
imp
im
p
- è praticamente indipendente dalla temperatura
- quindi anche il contributo delle collisioni con
le impurezze è indipendente dalla temperatura
(nei metalli, vF , m* , e la densità elettronica n
sono praticamente costanti)
imp
p
m*vF
m*vF
 2

n S
2 imp imp
ne limp
ne
Es.: supponiamo una frazione di impurità dell’ordine di qualche
parte su un milione e una sezione d’urto “geometrica” ( 10-20 m2)
1
limp
 nimp Simp  105 1029 m 3 10 20 m 2  104 m 1 ; vF  c
2E F
mc2
c
20eV
0,5 106 eV
 6 103 c
m*cvF 1
0,5 106 eV  6 10 3
imp 

10 4 m 1  1011 m
ne 2c limp 10 29 m 3e 1,6 10 19 C  3 108 ms 1
il contributo alla resistività delle impurità è dell’ordine del permille  RRR = T=300K / T
collisioni coi fononi
probabilità di collisione con i fononi:
-1/lfon è direttamente proporzionale alla densità di fononi, nfon,con costante di
proporzionalità Sfon pari alla “sezione d’urto elettrone-fonone”: 1/lfon = Sfon nfon
'
k el
- nfon dipende dalla temperatura: la distribuzione in
energia dei fononi a una data T si ottiene da quella
dei fotoni (spettro di corpo nero) sostituendo “vfon” a
“c” e tenendo conto che l’ max è limitato a Debye:
 Debye
n fon 

e
0
g ( )d
 / k BT

 Debye
12
 1 (v fon )
3

e
0
 / k BT
ad alta temperatura: e
n fon  C
 Debye
 k BT d  C
0
( )2 d
 / k BT
1
 Debye

C

k fon
( )2 d
 / k BT
e
1
0
 1   / kBT
2
k B Debye
2
urto
elettrone-fonone
T T
quindi la densità numerica di fononi è proporzionale a T

kel
conservazione
dell’energia
'
E el  Eel
  fon
conservazione della
quantità di moto

'

kel  kel  k fon
Si può determinare la costante di proporzionalità tenendo conto
che, a differenza di ciò che avviene per i fotoni, il numero di
oscillazioni possibili è fisso, pari a 3nat, cioè a 3 oscillazioni per
atomo (due trasversali e 1 longitudinale)
 Debye
12
 g ( )d  (v )3
fon
0
 Debye

( ) d  C
2
0
da cui si ottiene, ad alta temperatura:
 Debye

( ) d  3nat
2
0
collisioni
con i fononi
; C
9nat
3
 2 Debye
 Debye
9
T
n fon  nat
; D 
2 D
kB
quindi nfon, ad alta temperatura, è
- direttamente proporzionale a T
- direttamente proporzionale alla densità atomica nat
- inversamente proporzionale alla temperatura di Debye D , che è caratteristica
del cristallo (legata alla massima frequenza delle oscillazioni fononiche)
a bassa temperatura (T < D ), nfon T 3
Introducendo 1/lfon nell’espressione della resistività, si
ottiene (nei metalli, vF , m* , e la densità elettronica n
sono praticamente costanti)
dipendenza
della resistività
dalla temperatura
m*vF
m*vF
 fon (T )  2

n fon (T ) S fon (T )
2
ne l fon
ne
Ad alta temperatura, Sfon è costante, perché i fononi hanno praticamente la
frequenza max, Debye, nfon è proporzionale a T, quindi
d /dT = dfon /dT  Sfon
la variazione di  con la temperatura misura l’accoppiamento elettrone-fonone
 accoppiamento debole buon conduttore
 un accoppiamento sufficientemente forte può indurre comportamenti
superconduttivi
A bassa temperatura (T < D ), nfon T 3, inoltre Sfon diminuisce come T2, quindi
fon diminuisce come T5
le due componenti della resistività
“temperatura di Debye”
D 
 Debye
kB
Ciò che si vede dai dati
•l’estrapolazione lineare non
funziona a temperature molto
basse: la probabilità di urto
diminuisce, come atteso in base
alla diminuzione dei fononi
3
resistività 10^-8 ohm m
• a temperatura ambiente il
coefficiente termico è vicino al
valore aspettato dal modello di
Sommerfeld: 0,0038 K-1
dati di misura su
un campione di
rame “puro”
3,5
2,5
2
1,5
1
0,5
estrapolazione
lineare
0
-0,5
-300
-250
-200
-150
-100 -50
0
temperatura °C
50
100
150
resistività 10^-8 ohm m
14
12
dati di misura su un
campione con 3,5% di Mn
10
8
6
L’aggiunta di impurezze
riduce la dipendenza dalla
temperatura
dati di misura su un
campione di rame “puro”
4
2
0
0
50
100
temperatura °C
150
200
200
superconduttori
B or86_ann700
0 ,8
0 ,7
0 ,6
R ( )
0 ,5
temperatura
critica
Tc,onset = 34,5 K
0 ,4
0 ,3
RRR = 1,25
0 ,2
I = -500 A
0 ,1
Tc,zero = 31,1 K
0
-0 ,1
0
50
10 0
150
20 0
250
30 0
T (K)
Esperimento storico di
Kamerlingh Omnes (1911):
transizione superconduttiva
di Hg a 4,2 K
transizione
superconduttiva
B2 della temperatura
Figura
21. Grafico
della resistenzadiinMg
funzione
(HTCS: High Critical Temperature Superconductor )