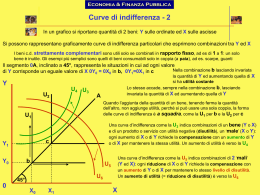
Utilità e curve di indifferenza - 7
Curve di indifferenza
Il legame tra ricchezza finale e investimento iniziale
in un portafoglio con rendimenti attesi Π è
W=(1+Π)W0. Anche se ciò vale solo sotto
specifiche restrizioni, assumiamo di avere una
funzione di utilità del soggetto avverso al rischio
per cui si può guardare solo ai rendimenti attesi e
alla varianza del portafoglio:
U = U(Πe,σ2Π) U1>0, U2<0, U11<0, U22<0
U1>0 utilità rendimento; U2<0 disutilità rischio; In
questo caso, le curve di indifferenza sono
1
convesse come segue
Utilità e curve di indifferenza - 8
Πe
I1
I2
C'''
A'''
A
A''
C
C''
(A - A'') = (C - C'')
σ2Π
2
Utilità e curve di indifferenza - 9
In un punto come A sulla curva di indifferenza I1 l’individuo
richiede un rendimento atteso più elevato (da A” a A”’)
quale compenso per il più elevato rischio (da A a A”) per
mantenere lo stesso livello di utilità: curve di indifferenza
con pendenza positiva nel piano rischio-rendimento.
Inoltre, curve di indifferenza convesse verso l’asse rischio:
nel punto C, per sopportare lo stesso aumento del rischio
(A–A”=C–C”) l’individuo (avverso al rischio) vuole un
maggiore aumento del rendimento atteso (A”–A”’<C”–
C”’).
Le curve di indifferenza nel piano rischio-rendimento atteso
ci serviranno nell’analisi del CAPM
3
Utilità e curve di indifferenza - 10
Utilità intertemporale
Vari modelli assumono che gli investitori derivano utilità
solo dal consumo. In ogni momento del tempo:
U = U(Ct) U’(Ct)>0, U”(Ct)<0
con una funzione di utilità simile a quella precedente del
soggetto avverso al rischio. La funzione generale di utilità
intertemporale sull’arco di vita è data da:
UN = U(Ct, Ct+1, Ct+2, …, Ct+N)
di solito si assume separabilità e tasso di sconto costante:
UN = U(Ct) + δU(Ct+1) + δ2U(Ct+2) +…+ δNU(Ct+N)
4
Utilità e curve di indifferenza - 11
Il tasso di sconto intertemporale dipende dalle preferenze
dell’individuo. Se definiamo δ = 1/(1+d) allora è il tasso
soggettivo di preferenza intertemporale, il tasso al quale
l’individuo accetta di scambiare consumo tra diversi
momenti del tempo.
In questo caso, le curve di indifferenza hanno la forma
tradizionale, cioè sono convesse verso l’origine nel piano
Ct, Ct+1
5
Investimento fisico e consumo ottimale - 1
Se i ricavi futuri fossero certi gli imprenditori
dovrebbero ordinare i progetti di investimento
fisico secondo il VAN (>0) o il TIR (>r).
Per l’economia nel suo complesso, gli investimenti
richiedono di rinunciare a consumo presente in
cambio di consumo futuro; ma tale scelta potrebbe
non essere coerente con le scelte dei consumatori.
Come fanno i mercati finanziari a ben coordinare le
scelte di investimento delle imprese e quelle di
cosumo/risparmio delle famiglie?
6
Investimento fisico e consumo ottimale - 2
Consideriamo un semplice modello a 2 periodi della scelta
di investimento con risultati certi (privi di rischio) ed
espressi in termini reali (inflazione=0).
Vedremo che in queste ipotesi vale un principio di
separazione: se ogni imprenditore massimizza il valore
dell’impresa, cioè investe fino a quando VAN=0 (ovvero
TIR=r), ciò consente ai consumatori di massimizzare il
benessere individuale scegliendo il profilo di consumo
desiderato.
In altri termini, scelta ottimizzante dell’impresa e scelta del
consumatore sono tenute separate: prima l’impresa sceglie
il livello di produzione e poi il consumatore va sul
mercato finanziario per dare o prendere fondi in modo da
ottenere il profilo temporale di consumo desiderato 7
Investimento fisico e consumo ottimale - 3
Scelta di ottimizzazione dell’impresa
Tutta la produzione è destinata a consumo o a investimento
fisico. L’imprenditore ha una dotazione iniziale W0. Egli
ordina i progetti di investimento per VAN decrescente
scontando col tasso di interesse privo di rischio r.
Destinando parte della dotazione iniziale a consumo
futuro C0(1), ottiene risorse per investire I0 = W0 – C0(1).
L’investimento fisico nel progetto con VAN più elevato
dà prodotto consumabile a t=1 in misura C1(1) > C0(1) (fig.
seguente). Il TIR del progetto (espresso in termini di
consumo) è:
1 + TIR(1) = C1(1) / C0(1)
8
Investimento fisico e consumo ottimale - 4
N.B.: A – A” = B – B”
Consumo al
periodo t=1
10° progetto di
investimento
B"
B
2° progetto di
investimento
C 1 (1)
A"
A
I0
C 0 (1)
1° progetto di
investimento
W0
Consumo al
periodo t=0
9
Investimento fisico e consumo ottimale - 5
A mano a mano che l’imprenditore assegna di più della sua
dotazione iniziale ad altri progetti di investimento con
VAN decrescente il TIR (C1/C0) cala dando luogo alla
curva delle opportunità di produzione (fig. precedente)
Il primo (e più produttivo) investimento ha:
VAN(1) = [C1(1)/(1+r)] – I0 > 0 e TIR(1) = C1(1) / C0(1) > r
Consideriamo ora il problema del finanziamento e
ricordiamo che il vincolo di bilancio intertemporale è una
linea retta (linea del mercato monetario) con pendenza (1+r) che dà la possibilità di prestare e indebitarsi sul
mercato
10
Investimento fisico e consumo ottimale - 6
Consumo al
periodo t=1
linea del mercato monetario
con pendenza - (1+r)
X
C1*
I0*
C0*
W0
Consumo al
periodo t=0
11
Investimento fisico e consumo ottimale - 7
L’imprenditore con dotazione iniziale W0 continua a
investire fin che TIR=r, punto in cui determina la coppia
(C0*, C1*) e anche I* = W0 – C0*
A destra di X, TIR>r mentre a sinistra TIR<r.
Ma scelte di investimento e di consumo sono coerenti?
Se il consumatore ha flussi di reddito nei due periodi pari a
VA, le sue possibilità di consumo sono:
VA = C0 + [C1/(1+r)]
Sia la funzione di utilità sull’arco di vita: U = U(C0, C1)
Il consumatore ha curve di indifferenza come segue e
determina la sua coppia ottimale (C0**, C1**) al punto di
tangenza con la linea di bilancio
12
Investimento fisico e consumo ottimale - 8
Consumo al
periodo t=1
Y
C 1 **
linea di bilancio
con pendenza - (1+r)
I2
I1
C 0 **
Consumo al
periodo t=0
13
Investimento fisico e consumo ottimale - 9
In generale non vi è garanzia che le coppie (C0*, C1*) e
(C0**, C1**) coincidano (vedi figura seguente): si
raggiunge l’equilibrio attraverso il mercato dei capitali.
L’imprenditore ha prodotto il profilo di consumo (C0*, C1*)
che massimizza il valore dell’impresa. Supponiamo che lo
paghi in forma di dividendo. Il VA* di questo flusso di
cassa è: VA* = C0* + [C1*/(1+r)]
Esso è pagato al consumatore (anche proprietario impresa).
Ma, in condizioni di certezza, il consumatore può
scambiare il flusso VA* per ogni combinazione tale che:
VA* = C0 + [C1/(1+r)] quindi, prendendo e dando
credito (al tasso r), può raggiungere la coppia desiderata
(C0**, C1**)
14
Investimento fisico e consumo ottimale - 10
Consumo al
periodo t=1
linea del mercato monetario
e di bilancio
con pendenza - (1+r)
Y
C 1 **
X
C1*
L
C 0 **
I0*
C0*
W0
Consumo al
periodo t=0
15
Investimento fisico e consumo ottimale - 11
In generale, dunque, il principio di separatezza ci
aiuta a risolvere il problema di ottimizzazione in
due stadi e noi ci concentreremo su come fa il
consumatore a:
1. Allocare il proprio portafoglio tra varie attività
con diverso grado di rischio (CAPM);
2. Raggiungere il profilo di consumo desiderato
usando il mercato dei capitali.
16