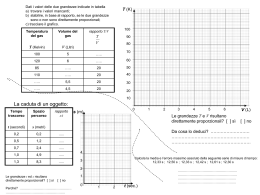
Grandezze proporzionali
Grandezze direttamente proporzionali
 Costruiamo insieme la legge:
consideriamo un insieme di rettangoli aventi una
dimensione quadrupla dell’altra
2 cm
1 cm
4 cm
8 cm
Grandezze direttamente proporzionali (1)
 Costruiamo la tabella
Altezza (x)
Base (y)
1
2
3
……….
1/2
4
8
12
……….
2
Osserviamo che:
• Per ogni riga: il RAPPORTO
tra valori corrispondenti è
costante
• Per ogni colonna: al
raddoppiare, triplicare,
dimezzare … della x, anche la y
raddoppia, triplica, dimezza ….
y
4
x
Grandezze direttamente proporzionali (2)
 L’altezza x e la base y sono due
grandezze DIRETTAMENTE proporzionali.
 In generale:
Grandezze direttamente proporzionali (2)
Due grandezze x e y sono
DIRETTAMENTE PROPORZIONALI
se sono legate da una legge del tipo
y
 k(costante)
x
ovvero
y=kx
k 
 Quale grafico per x e y?
Grandezze direttamente proporzionali (3)
Una funzione del tipo
y  k x
y (base)
Diagramma di y=4x
10
8
6
4
2
0
0
0,5
1
1,5
x (altezza)
Prova
tu
2
2,5
che esprime la legge
della proporzionalità
diretta, ha per
diagramma una
SEMIRETTA
AVENTE L’ORIGINE
NELL’ORIGINE DEGLI
ASSI
Grandezze inversamente proporzionali
 Costruiamo insieme la legge:
consideriamo un insieme di rettangoli equivalenti,
di area 12 cm2
2 cm
3 cm
12 cm2
12 cm2
6 cm
4 cm
Grandezze inversamente proporzionali (1)
 Costruiamo la tabella
Altezza (x)
Base (y)
1
2
3
12
6
4
……….
1/2
……….
24
x  y  12
Osserviamo che:
• Per ogni riga: il
PRODOTTO tra valori
corrispondenti è
costante
• Per ogni colonna: al
raddoppiare, triplicare,
dimezzare … della x, la
y dimezza, diventa 1/3,
raddoppia ….
Grandezze inversamente proporzionali (2)
 L’altezza x e la base y sono due grandezze
INVERSAMENTE proporzionali.
 In generale:
Grandezze inversamente proporzionali (2)
Due grandezze x e y sono
INVERSAMENTE PROPORZIONALI
se sono legate da una legge del tipo
x  y  k(costante)
ovvero
k
y
x
k 
 Quale grafico per x e y?
Grandezze inversamente proporzionali (3)
y (base)
Diagramma di x∙y = 12
Una funzione del tipo
k
y
x
60
50
40
30
20
10
0
0
1
2
3
x (altezza)
Prova
tu
4
5
che esprime la legge
della proporzionalità
inversa, ha per
diagramma un
RAMO DI IPERBOLE
EQUILATERA
Prova tu …
 Le seguenti funzioni esprimono leggi di
proporzionalità diretta:
y
2
x
y 3

x 4

y  2x

3
y x
4
 Prova a rappresentarle in forma cartesiana
Prova tu …
 Le seguenti funzioni esprimono leggi di
proporzionalità inversa:
xy  10

xy  25

10
y
x
25
y
x
 Prova a rappresentarle in forma cartesiana