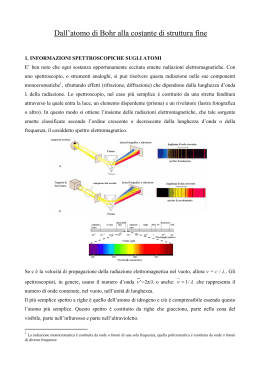
Lezione 2
Il modello atomicoplanetario di Bohr
a
1
ipotesi di Bohr
Esiste uno stato stazionario dell'atomo
caratterizzato da particolari orbite circolari lungo
le quali gli elettroni si muovono senza emettere
radiazioni elettromagnetiche. Gli elettroni che
percorrono tali orbite stazionarie possiedono una
certa quantità ben definita di energia detta livello
energetico dell'orbita
2
2
mv
e
k 2
r
r
Forza centrifuga = attrazione elettrica
2
ke
r
mv2
1 elettronvolt = 1eV
-19
=1,60·10
Energia di un quanto di luce (fotone),
relazione di Plank : E = h·f
(nel vis. IR freq ~ 1·1015 hertz)
E(J) = h·f = 6,626·10-34(J·s) · freq(Hz)
E ~ 10-19
E(eV) = h·f = 4,141·10-15(eV·s) · freq(Hz)
E ~ 1..10
J
1 
 1
 RH  2  2 

m 
2
1
1 
 1
 RH  2  2 

m 
n
1
1 
 1
 RH  2  2 

m 
2
1
1 
 1
 RH  2  2 

m 
n
1
Nel 1855 J. Balmer, studiando le righe emesse dall'idrogeno, scoprì una relazione
matematica che permetteva di ottenere il reciproco della lunghezza d'onda delle singole
righe spettrali.con m = 3,4,5,6.... ed RH costante di Rydberg per l'idrogeno.
RH = 10973731,568
La relazione di Balmer può essere generalizzata sostituendo al numero 2 un intero n
minore di m.
In tal modo, è possibile prevedere per l'idrogeno l'esistenza, oltre alle 4 righe nel visibile (
una nel rosso, una nell'azzurro e due nel blu-violetto), anche altre serie, una
nell'ultravioletto (serie di Lyman per n = 1) e 3 nell'infrarosso (serie di Paschen per n = 3;
serie di Brackett per n = 4; serie di Pfund per n = 5), in seguito scoperte.
La spiegazione della relazione di Balmer venne dal modello planetario
dell’atomo di Bohr e fu una delle sue principali apparenti conferme.