LABORATORIO DI ASTROFISICA II
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
Programma del Corso
Calendario esercitazioni
Elenco dei gruppi 2007
Telescopi, Montature, Oculari
Diffrazione e interferenza, reticoli, spettrografi a reticolo
Lo spettrografo OMR-10C
Aberrazioni ottiche
Spettrografi a prisma
La riduzione di dati CCD
misura di lunghezze d'onda con lo spettroscopio a prisma
misura della figura di diffrazione prodotta da una fenditura
Classificazione spettrale
Fibre ottiche, spettrografi multioggetti ed echelle
Analisi degli spettri TACOR
Applicazioni astronomiche della spettroscopia
Telescopi
O = obiettivo
Oc = oculare
f = lunghezza focale dell'obiettivo
fe = lunghezza focale dell'oculare
Pe = pupilla di entrata (diametro dell'obiettivo) Pu = pupilla di uscita
u = campo di vista reale
U = campo di vista apparente
t = piano focale
Ep = estrazione pupillare
Definizioni:
Scala sul piano focale (s, tipicamente secondi d'arco per millimetro)
si ricava dalla relazione tg (u) = (1 mm)/f ; per u piccolo, tg (u) ~ u, per cui s=206265"/f.
Per un telescopio con f = 2 metri , s ~ 100"/mm
Ingrandimento: e' il rapporto tra U e u, ovvero tra Pe e Pu. Per una sorgente a distanza infinita
(caso astronomico) e' uguale al rapporto tra le lunghezze focali dell'obiettivo e dell'oculare f/fe.
Apertura: rapporto tra lunghezza focale e pupilla di entrata dell'obiettivo f/Pe. Per i rifrattori
classici e' tipicamente 10-15, per i riflettori 5-10.
•
il telescopio rifrattore di Galileo. 1610, obiettivo convergente, oculare divergente.
•
il telescopio rifrattore di Fraunhofer. 1818, obiettivo acromatico convergente, oculare
convergente. F/12
•
il telescopio riflettore di Newton. 1670, obiettivo parabolico e specchio di rinvio piano. F/6
•
il telescopio di Gregory. 1663, obiettivo parabolico e specchio secondario ellittico. F/10
•
il telescopio di Cassegrain. 1672 , obiettivo parabolico e specchio secondario iperbolico. La
versione modificata di Ritchey e Chretien ha entrambi gli specchi iperbolici. F/8
•
il telescopio di Schmidt. 1920, obiettivo sferico e lastra correttrice di 4 ordine. Piano focale
curvo. F/3. Grande campo (5 gradi).
•
il telescopio di Maksutov. Tutte le superfici sono sferiche, a differenza dello Schmidt.
•
il telescopio di Maksutov semplificato.
•
il telescopio tipo Schmidt-Cassegrain. Obiettivo e secondario sferici, lastra correttrice tipo
Schmidt. F/10.
Montature
Lo scopo della montatura di un telescopio e' duplice:
•
•
a) permettere il puntamento dello strumento nella direzione desiderata
b) permettere di compensare il moto di rotazione terrestre per mantenere il puntamento
desiderato
La montatura dispone pertanto di due assi ortogonali intorno ai quali può ruotare lo strumento. Il
moto avviene normalmente per mezzo di motori elettrici, spesso asserviti a un calcolatore
elettronico.
Ci sono sostanzialmente due tipi di montatura in uso, altazimutale ed equatoriale
La montatura equatoriale ha un asse orientato parallelamente all'asse polare terrestre.
La montatura altazimutale ha un asse verticale e l'altro orizzontale.
Il vantaggio della montatura equatoriale e' di permettere di compensare il moto terrestre di
rotazione agendo su un solo asse (asse polare), ma deve essere più robusta e pesante perché l'asse
polare e' inclinato rispetto alla verticale.
Il vantaggio della montatura altazimutale e' di essere più leggera, ma ha i seguenti svantaggi:
a) richiede il moto simultaneo su due assi: questo problema e' diventato poco importante con
l'asservimento del moto del telescopio a un calcolatore elettronico.
b) il campo osservato ruota durante la posa rispetto al piano focale: ciò richiede la presenza di un
derotatore di campo per compensare l'effetto. Anche il moto del derotatore deve essere asservito al
calcolatore.
c) e' impossibile mantenere l'inseguimento mentre il campo passa allo zenit.
Tutti i grandi telescopi moderni sono a montatura altazimutale. Questa si stà diffondendo anche
tra i piccoli telescopi amatoriali con puntamento controllato da PC.
Tra i grandi telescopi riflettori a montatura altazimutale (qualunque sia lo schema ottico) e'
oramai molto diffuso il fuoco Nasmith che consente di avere la strumentazione di piano focale
permanentemente orizzontale, con grandi vantaggi di stabilità meccanica. Il fuoco Nasmith si
trova sull'asse di altezza (orizzontale) e viene raggiunto deviando il fascio di luce con uno specchio
piano, posto sull'incrocio del fascio ottico con l'asse suddetto, inclinato a 45 gradi. Ruotando lo
specchio di 180 intorno all'asse ottico si può far uscire il fascio di luce sull'una o l'altra estremità
dell'asse di declinazione ed avere così due strumenti diversi permanentemente montati a ciascun
fuoco Nasmith.
Oculari
L'oculare e' una lente, o più spesso un gruppo di lenti, che serve per ingrandire l'immagine
formata dall'obiettivo sulla sua superficie focale e consentirne l'osservazione all'occhio.
Ci sono concettualmente due tipi di oculari, quelli divergenti e quelli convergenti.
L'oculare divergente e' stato storicamente il primo ad essere usato (telescopio di Galileo) ma
produce immagini di cattiva qualità ed e' attualmente usato solo nei binocoli da teatro a basso
ingrandimento e piccolo campo di vista. Inoltre, poiché va collocato prima del piano focale
dell'obiettivo, non permette l'uso di crociere di puntamento o di reticoli per misure di distanze
angolari. Tutti gli oculari di uso comune sono quindi del tipo convergente.
Per l'uso pratico sono importanti le seguenti caratteristiche:
s = distanza focale ; Ep = estrazione pupillare ; w' = campo apparente
P = somma Petzval (inverso del raggio di curvatura della superficie focale)
La distanza focale determina l'ingrandimento, che e' il rapporto tra la focale dell'obiettivo e quella
dell'oculare. Esistono in pratica un ingrandimento minimo ed uno massimo utile per un dato
obiettivo:
•
•
quello minimo e' quello che fornisce una pupilla di uscita di diametro pari alla pupilla
dell'occhio adattato al buio (circa 6 mm)
quello massimo e' quello che fornisce una immagine sufficientemente luminosa da poter
essere vista con buon contrasto;
poiché e' l'energia raccolta dall'obiettivo che produce l'immagine sul piano focale, maggiore
e' l'ingrandimento minore sarà la brillanza superficiale dell'immagine. Al di sotto di una
certa soglia (soggettiva) l'occhio non sarà capace di distinguerne i dettagli.
L'ingrandimento massimo e' circa 3 volte il diametro dell'obiettivo. In pratica la turbolenza
dell'atmosfera terrestre rende inutile superare i 500 ingrandimenti
L'estrazione focale dice a che distanza dall'oculare va messo l'occhio: una estrazione focale troppo
piccola facilita l'appannamento delle lenti. Inoltre impedisce l'osservazione con gli occhiali.
Il campo apparente determina quale porzione della superficie focale e' osservabile; ovviamente e'
più difficile realizzare un campo apparente grande.
I primi oculari, a parte le semplici lenti divergenti (Galileo) e convergenti (Keplero) avevano due
sole lenti. L'oculare di Hyugens (1703), ancora molto usato e di facile realizzazione, ha lo
svantaggio che il piano focale e' tra le due lenti, quindi non permette l'uso di un micrometro.
Per ovviare a ciò Ramsden (1783) dispose le lenti in modo diverso, con lo svantaggio di avere una
estrazione pupillare praticamente nulla.
Un sostanziale miglioramento fu introdotto da Kellner (1849) sostituendo la lente dell'occhio con
un doppietto acromatico ed aumentando l'estrazione focale. Anche questo oculare e' relativamente
economico ed e' tuttora usato. Tutti questi oculari "storici" hanno le lenti piuttosto distanti tra
loro. Ciò produce una forte curvatura di campo e notevoli riflessi, anche perché all'epoca non
esistevano i moderni trattamenti antiriflessi. Nella seconda metà del 1800 si progettarono perciò
oculari che minimizzassero questi problemi.
Storicamente fu importante l'oculare "monocentrico" di Steinheil (1865) che non ha praticamente
riflessi, ma ha un campo limitato.
Tra gli oculari "di seconda generazione" ci sono quelli di Konig, di Abbe ( o ortoscopico), di Plossl,
di Erfle e di Bertele (1920) tuttora molto usati con leggere modifiche, dovute soprattutto ai
progressi nelle tecnologie di produzione di vetri ottici con gli indici di rifrazione desiderati.
curva 1 = cromatica laterale, in millesimi della focale
curva 2 = focale meridiana in millimetri, per una focale di 100 mm
curva 3 = focale sagittale (stesse unità)
in ordinata la distanza dal centro del campo (in gradi) .
Diffrazione e Interferenza
Richiami sulle onde, Diffrazione da una fenditura, Diffrazione da 2 fenditure,
Reticolo di diffrazione, Spettroscopi a reticolo,
Il grism
Il BFOSC dell'Osservatorio di Bologna
Richiami sulle onde
La scoperta della diffrazione della luce ha portato all'abbandono della teoria corpuscolare, e alla
nascita della teoria ondulatoria. La trattazione della luce come onda e' indispensabile in ottica
quando si ha a che fare con dimensioni confrontabili con la lunghezza d'onda della luce ( 0.5
micrometri per la luce visibile).
Dal punto di vista fisico la luce e' un'onda elettromagnetica trasversale descrivibile con una
equazione del tipo
y = f(x - vt)
dove x e' la direzione di propagazione dell'onda, t il tempo, v la velocità dell'onda e y la direzione
(ortogonale ad x) in cui oscilla il vettore campo elettrico. Il segno - indica che l'onda si propaga nel
verso delle x crescenti.
Possiamo assumere che la forma della funzione f sia una semplice sinusoide per cui
y = A cos[ K(x - vt) ]
con A e K costanti.
Se indichiamo con T il periodo della oscillazione del campo, si chiama lunghezza d'onda lambda
lo spostamento del profilo dell'onda nel tempo T, ovvero la distanza tra due massimi consecutivi.
La costante K e' allora pari a 2π/λ e si chiama numero d'onda. Introducendo la pulsazione legata
alla frequenza ν dalla relazione Ω =2π/ν , l'equazione dell'onda sinusoidale diventa
y = A sin(Kx - Ω t)
La velocità con cui si propaga l'onda si chiama velocità di fase e vale la relazione
v = λ/T = λν
Si chiama intensità dell'onda l'energia che fluisce nell'unita' di tempo attraverso una superficie
unitaria normale alla direzione di propagazione dell'onda ed e' proporzionale al quadrato della
ampiezza A.
Poiché la frequenza di un'onda e' costante, mentre la velocità e' v = λν, la lunghezza d'onda della
radiazione e' proporzionale alla velocità di propagazione nel mezzo considerato.
Si chiama cammino ottico di una radiazione, in un mezzo di indice di rifrazione n e di lunghezza
d, il prodotto nd, e rappresenta il cammino che la radiazione avrebbe percorso nello stesso tempo
nel vuoto (che ha indice di rifrazione n=1).
Si definisce infine "fronte d'onda" il luogo geometrico dei punti dello spazio in cui la radiazione ha
uguale fase. Per una sorgente puntiforme immersa in un mezzo omogeneo e isotropo i fronti
d'onda sono superfici sferiche concentriche centrate sulla sorgente e in espansione con uguale
velocità. A grandissima distanza dalla sorgente i fronti d'onda sono praticamente superfici piane e
si parla in questo caso di "onde piane".
Diffrazione da una fenditura
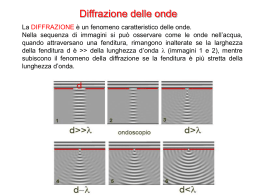
Si verifica sperimentalmente che quando un'onda attraversa una apertura o colpisce l'estremità di
un ostacolo invade sempre parzialmente la regione di spazio circostante. Questo fenomeno, noto
come DIFFRAZIONE, vale sia per le onde trasversali che longitudinali (es. onde sonore).
Se noi illuminiamo una parete con la luce proveniente da una stretta fenditura verticale vediamo
sulla parete non una singola banda verticale di luce ma una serie di bande (frange di diffrazione)
di intensità decrescente dal centro.
Per spiegare questo fatto Huygens propose la seguente regola:
Principio di Huygens
"ciascun punto di un fronte d'onda si può considerare come una nuova sorgente di onde di uguale
frequenza".
Questo principio poteva spiegare il fenomeno dell'interferenza, scoperto da Thomas Young nel
1801 facendo passare la luce attraverso due strette fenditure illuminate dalla stessa sorgente
e di calcolare la posizione delle frange e la loro intensità relativa.
Diffrazione da 2 fenditure
Il principio alla base del calcolo delle posizioni delle frange di interferenza e' il seguente: in un
punto dello spazio a valle delle fenditure le onde possono trovarsi in fase tra loro solo se le
distanze dalle fenditure differiscono di un numero intero di lunghezze d'onda (figura).
Se le onde sono in fase i campi elettrici si sommano e l'intensità luminosa e' alta, se sono in
controfase i campi si annullano e la intensità e' zero.
A rigore i luoghi di ugual fase sono delle iperboli; a distanze grandi rispetto alla distanza tra le
fenditure sono praticamente delle rette.
Se chiamiamo D la distanza tra i centri delle due fenditure, d la larghezza di ciascuna fenditura, λ
la lunghezza d'onda della radiazione e θ il generico angolo di uscita, perché ci sia interferenza
costruttiva occorre che sia D sin(θ)=m λ, dove m e' un numero intero.
La distribuzione di intensità luminosa su uno schermo posto a grande distanza dalle fenditure
(grande rispetto a D) e' data dalla figura seguente.
Notare che la larghezza dei massimi di interferenza e' sensibilmente minore della larghezza del
loro inviluppo, che e' la figura di diffrazione di una singola fenditura.
Reticolo di diffrazione
Se invece di due sole fenditure ne mettiamo molte (N), equispaziate e di uguale larghezza,
otteniamo quello che si suole chiamare un RETICOLO di diffrazione,
che produce sullo schermo la seguente distribuzione di luce, caratterizzata da stretti ed intensi
massimi principali e numerosi (N-1) deboli massimi secondari tra due massimi principali.
Quanto più numerose sono le fenditure, tanto più deboli sono i massimi secondari e tanto più
stretti e intensi i massimi principali.
La distanza tra due fenditure adiacenti si chiama PASSO del reticolo.
I vari massimi principali si chiamano ordini, con lo zero che indica il massimo centrale.
•
•
Il rapporto di intensità tra i massimi principali e quelli secondari e' proporzionale ad N2.
Le posizioni degli ordini sono date dalla relazione
D sin(θ) = mλ,
con m intero.
•
La larghezza degli ordini e' data dalla relazione
dθ = λ/[ ND cos(θ) ] .
Possiamo definire la dispersione angolare e il potere risolutivo cromatico del reticolo di diffrazione:
•
•
dispersione angolare, dθ/dλ = m/Dcos(θ) ; e' proporzionale al numero dell'ordine. Per
angoli di dispersione piccoli cos(θ) varia poco con θ e la dispersione e'
approssimativamente lineare. In pratica la dispersione può essere ben modellata con un
polinomio di terzo grado.
potere risolutivo R, λ/dλ = Nm, con m ordine ed N numero di tratti del reticolo
effettivamente illuminati dal fascio luminoso.
I reticoli di diffrazione che si adoperano in pratica hanno da 100 a 2400 fenditure per millimetro e
sono lunghi diversi centimetri, sicché sono costituiti da migliaia (fino a centinaia di migliaia) di
fenditure. In queste condizioni i massimi secondari sono assolutamente indistinguibili.
Se invece di far incidere il fascio di luce perpendicolarmente al reticolo lo si manda con un certo
angolo di incidenza θ1, la condizione di interferenza costruttiva diventa
D (sin(θ1)+sin(θ2))= mλ
dove θ2 e' la direzione di uscita.
E' da notare che la distribuzione di energia tra i vari picchi di interferenza e' simmetrica ed
avviene privilegiando il picco centrale, mentre quelli più deviati dalla direzione del fascio incidente
sono sempre più deboli.
Il reticolo di diffrazione permette di effettuare misure assolute di lunghezza d'onda, noto il passo,
tramite la misura dell'angolo al quale avviene la interferenza costruttiva.
Ovviamente non si può usare a questo scopo l'ordine zero, che e' sfortunatamente il più intenso,
in quanto la sua posizione non dipende dalla lunghezza d'onda della luce.
Luce policromatica
Se invece di un fascio di luce monocromatica si invia sul reticolo un fascio che contiene diverse
lunghezze d'onda, ciascuna di esse creerà la sua immagine di interferenza e ci saranno diversi
picchi di intensità in corrispondenza di ciascun ordine: se l'intervallo di lunghezze d'onda e'
grande e' possibile che il picco del primo ordine di una particolare λ vada a sovrapporsi a quello
del secondo ordine di una λ minore, come si può facilmente ricavare dall'equazione del reticolo.
Finora abbiamo considerato reticoli che lavorano per trasmissione, ma nella pratica sono più
usati reticoli che lavorano per riflessione, in quanto più efficienti. In questi reticoli la luce viene
fatta riflettere su scanalature inclinate incise sulla superficie del reticolo e ricoperte di un
materiale riflettente; per migliorare ulteriormente l'efficienza dei reticoli si usa un trucco
ingegnoso, che consiste nell'inclinare le scanalature in modo che un particolare ordine (di solito il
primo o il secondo) si formi nella direzione in cui si avrebbe la riflessione della luce incidente
secondo la legge di Snell: nella figura questa direzione e' indicata come β=0. Questi reticoli
vengono chiamati reticoli "blazed" o "a scaletta"). Anche i reticoli a trasmissione possono essere
"blazed": in questo caso si fa in modo che l'ordine desiderato capiti in corrispondenza della
direzione di rifrazione della luce.
Spettroscopi a Reticolo
Uno spettroscopio a reticolo e' concettualmente analogo ad uno a prismi. E' costituito da un
collimatore, un reticolo che sostituisce il prisma come elemento disperdente, e da un focheggiatore
che raccoglie lo spettro sul suo piano focale. In alcuni modelli il reticolo e' curvo in modo da poter
svolgere anche il ruolo di focheggiatore.
Tra i disegni classici ci sono:
•
quello di Rowland in cui il reticolo e' sferico e funge sia da collimatore che da
focheggiatore: in questo caso il fuoco del telescopio, il reticolo e lo spettro ottenuto stanno
sulla stessa circonfereza (circolo di Rowland). Questa configurazione e' adatta per uno
strumento da laboratorio ma non si presta ad essere attaccata ad un telescopio. Rowland
(1848-1901) fu uno dei pionieri della spettroscopia astronomica, ideò il reticolo sferico e
fece un atlante dettagliato dello spettro solare (1888).
•
quello di Littrow che usa un unico obiettivo sia come collimatore che come focheggiatore.
•
quello di Wadsworth che usa pure un reticolo curvo in modo da utilizzarlo anche come
elemento di focheggiamento; e' più compatto del Rowland e quindi più adatto ad essere
attaccato a un telescopio.
•
quello di Czerny-Turner che e' molto compatto.
Poiché il telescopio deve inseguire la stella durante la posa, ne viene la necessità di verificare che
la stella sia dentro la fenditura ed eventualmente correggere il puntamento. Ciò si realizza con
un'ottica dedicata. La guida veniva fino a poco tempo fa eseguita manualmente dall'astronomo,
oggi una camera CCD e un PC o microprocessore dedicato hanno sostituito l'occhio e il cervello
umano.
Uno spettrografo e' comunque uno strumento abbastanza pesante, in quanto deve essere molto
rigido per garantire l'allineamento delle ottiche comunque venga orientato il telescopio. Gli
spettrografi ad alta risoluzione non sono quindi attaccati al telescopio ma vengono messi al fuoco
coude' (per telescopi con montatura equatoriale) o al fuoco Nasmith per quelli a montatura
altazimutale.
Il Grism
Il Grism e' l'accoppiamento di un reticolo di diffrazione in trasmissione e di un prisma sottile. Il
reticolo può essere inciso direttamente sul prisma o incollato. L'elemento disperdente in questo
caso e' il reticolo, mentre il prisma ha il solo compito di riallineare la direzione della lunghezza
d'onda centrale dello spettro in uscita (generalmente il primo ordine) nella direzione dell'asse
ottico, analogamente al prisma di Amici.
Il nostro telescopio didattico TACOR
ha in dotazione un grism da 207 tr/mm (D = 4.83 µ) blazed al primo ordine. Dall'equazione del
reticolo, l'angolo di uscita che deve essere raddrizzato dal prisma e' δ ~7° ; poiché l'indice di
rifrazione del vetro Crown e' n=1.516 a 0.6 µ, il prisma deve avere un angolo di 7/(1-n) = 13.8° .
L'uso dei grism e' ottimale in fascio parallelo, ma può essere usato anche in fascio convergente
come il prisma di Amici se il rapporto focale F/# del telescopio e' grande ( > 8 ). L'uso dei grism in
fascio parallelo si e' molto esteso negli ultimi anni permettendo la realizzazione di strumenti
combinati camera-spettrografo, che permettono di utilizzare un telescopio sia per immagini dirette
che per spettroscopia senza dover cambiare strumento, semplificando quindi la gestione.
Il primo strumento di questo tipo e' stato EFOSC sviluppato all'ESO (European Southern
Observatory) per il telescopio da 3.6 m. Oggi strumenti simili si trovano in diversi Osservatori, in
Italia ad Asiago ed a Loiano.
Un esempio di strumento professionale, il BFOSC dell'Osservatorio di Bologna.
Lo spettrografo OMR10-C del TACOR
Un disegno classico di spettrografo astronomico, realizzato da diversi costruttori, e' realizzato
secondo il seguente schema:
Questo spettrografo e' in dotazione al nostro laboratorio: il collimatore ha una focale di 225 mm
f/9, il focheggiatore 135 mm f/2.8, la fenditura e' intercambiabile e può essere da 50 o 100
micron; anche il reticolo, e' intercambiabile e noi ne abbiamo uno da 240 tr/mm e uno da 600
tr/mm blazed al primo ordine a 500 nm.
Lo spettrografo e' dotato di due lampade a righe di emissione, rispettivamente al Mercurio e al
Neon, azionabili separatamente con appositi interruttori.
La descrizione completa dello strumento si trova qui.
Un elenco completo delle righe spettrali delle lampade e' ancora in fase di completamento.
Righe stellari, righe del Mercurio, righe del Neon, lampade dell'OMR-10C
Principali righe negli spettri stellari
3770 H11
3798 H10
3835 H9
3889 H8
3934 CaII
3968 CaII
3970 H epsilon (o H7)
4009 He I
4026 He I
4046 Fe I
4077 Sr II
4102 H delta
4121 He I
4128-30 Si II
4144 He I
4172-8 Ti II, Fe II
4200 He II
4227 CaI
4233 Fe II
4290-4300 CrI-CH
4314 Banda G (blend di righe metalliche)
4325 Fe I
4340 H gamma
4383 Fe I
4387 He I
4395-00 Ti II, Fe II
4417 Ti II, Fe II
4444 Ti II, Fe II
4471 HeI
4481 Mg II
4542 He II
4634-42 N III
4686 He II
4780 TiO (banda molecolare)
4861 H beta
4923 He I
4995 TiO (banda molecolare)
5167 MgH (banda molecolare)
5167-73-84 MgI
5270 FeI
5470 TiO (banda molecolare)
5890-96 NaI
6160-6240 TiO (banda molecolare)
6563 H alfa
Principali righe del Mercurio </STRONG < H1>
3652.0
3663.0
4046.6
4077.0
4358.4
5460.7
5769.7
5790.7
Principali righe del Neon
5330.8
5341.1
5400.6
Righe delle lampade dello spettrografo OMR-10C
Elemento
Hg
Hg
Hg
Ne
?
Ne
Ne
Ne
Ne
Ne
Ne
Ne
?
Ne
Ne
Ne
Ne
Ne
Ne
Ne
Ne
Ne
?
Ne
Hg
Ne
?
Ne
Ne
?
Hg
?
?
Hg
Hg
?
?
Hg
?
Hg
?
lambda(A)
5461
5770
5790
5852
5879
5945
5975
6029
6074
6143
6163
6217
6266
6304
6334
6382
6402
6506
6532
6600
6678
6717
6904
6929
6965
7032
7064
7164
7245
7270
7383
7430
7486
7503
7514
7585
7598
7635
7681
7723
7853
intensità relativa
33.2
17.4
18.9
7.7
1.5
2.0
1.2
1.2
2.0
3.7
1.6
1.3
2.5
1.3
2.1
2.8
4.9
2.7
1.5
1.8
2.7
2.0
1.3
2.2
1.5
3.9
1.5
1.1
1.8
1.1
1.7
1.2
1.2
1.9
1.8
2.1
3.0
3.9
1.4
1.9
1.3
Caratteristiche costruttive
Le caratteristiche principali di uno spettrografo sono:
•
•
•
•
larghezza della fenditura Lf
lunghezza focale ed apertura del collimatore Fc
lunghezza focale ed apertura del focheggiatore Ff
numero di tratti/mm e diametro del reticolo.
Queste grandezze determinano l'efficienza dello strumento, il suo potere risolutivo spaziale e
cromatico: uno spettrografo calcolato per lavorare con un dato telescopio può dare cattivi risultati
con uno molto diverso.
•
•
•
•
la fenditura e' la sorgente di luce dello spettrografo e si trova sul piano focale del
telescopio. Per avere alta efficienza deve essere abbastanza larga da contenere tutta la luce
della stella, ma per dare una elevata risoluzione cromatica deve essere molto stretta.
Per esempio, il nostro telescopio didattico di 2,35 metri di focale (scala 87. 8 "/mm), con
una turbolenza atmosferica di due arcsec (seeing 2") forma una immagine di una stella
larga 22.8 micron (FWHM, larghezza a metà altezza del suo profilo di luminosità).
In corrispondenza dell'immagine della stella, lo spettrografo darà, per ogni lunghezza
d'onda, lo spettro che e' la somma della luce della stella più quella di un'area di cielo larga
quanto la fenditura e alta quanto l'immagine di seeing della stella:
se la fenditura e' larga, per esempio, 100µ, il contributo del fondo cielo viene da un'area di
~ 23 x 100µ.
Ciò può essere poco importante per stelle brillanti ma tragico per stelle deboli. Lo
spettrografo OMR-10C ha in dotazione due fenditure, da 50 e 100 µ, che sono quindi più
larghe del seeing tipico, quindi troppo larghe per la focale del telescopio.
E' da notare che, se non ci fosse la fenditura, in ciascun punto del rivelatore la brillanza
superficiale sarebbe quella del cielo integrata su tutte le lunghezze d'onda, come in visione
diretta: la fenditura quindi, anche se non ottimale, contribuisce moltissimo a migliorare il
rapporto segnale/rumore su ciascun punto dello spettro.
Una fenditura larga presenta comunque il vantaggio di avere sempre la stella dentro la
fenditura anche se la guida non e' accuratissima, come e' spesso il caso per piccoli
telescopi.
L'apertura del collimatore (F/D) deve essere uguale quella del telescopio: se maggiore,
perde parte della luce raccolta dal telescopio, se minore e' inutilmente costoso (un obiettivo
più grande e' più caro...). Il collimatore dell'OMR-10C ha una focale di 225 mm f/9, quindi
ha un obiettivo da 25 mm. Questo dovrà essere anche il diametro del reticolo se non
vogliamo perdere potere risolutivo cromatico.
Il diametro del reticolo deve essere uguale al diametro del collimatore, visto che dal
collimatore esce il fascio di onde piane che devono illuminare il reticolo: se il reticolo e'
piccolo perde luce, se e' grande e' inutilmente costoso.
Il focheggiatore forma l'immagine della fenditura sul suo piano focale. La scala angolare su
questo piano e' quella del telescopio moltiplicata per il rapporto Fc/Ff: per il nostro
spettrografo OMR-10C il rapporto e' 1.66, quindi la scala e' 87.8 x 1.66 = 146 "/mm.
Il diametro (FWHM) di una stella con un seeing di 2" sarà quindi 13.7 µ.
Lo strumento e' ben adattato al telescopio se la risoluzione in lunghezza d'onda e'
confrontabile con la risoluzione angolare in cielo.
Vediamo ora quale é la risoluzione del reticolo.
•
L'equazione fondamentale del reticolo e'
D sin(θ)=m λ
dove:
D e' il passo del reticolo, λ la lunghezza d'onda, m l'ordine dello spettro considerato e θ
l'angolo di incidenza della luce sul reticolo.
La dispersione angolare prodotta da un reticolo e'
dθ/dλ = m/[D cos(θ)]
con un reticolo a 600 tr/mm ( passo D = 1.666µ), per λ = 0.5µ abbiamo θ = 17.5° e la
dispersione viene 0.629 rad/µ (36°/µ).
Lo spettro visibile ( 0.4 µ - 0.7µ) occupa quindi 10.8° che, con una focale di 135 mm,
corrispondono a 25.7 mm: la scala delle lunghezze d'onda e' quindi (~117 A/mm).
Questo dato ci permette di stabilire quale intervallo di lunghezze d'onda e' osservabile
simultaneamente con un rivelatore di dimensioni note, ovvero di che rivelatore abbiamo
bisogno per osservare un certo intervallo di lunghezze d'onda.
Il TACOR ha una camera CCD Starlight Xpress, modello MX916, con un sensore di 752 x
580 pixel rettangolari da 11.6 x 11.2 µ, corrispondenti a 8.7x 6.5 mm. L'intervallo
spettrale coperto da questa camera e' quindi
8.7mm X 117 A/mm = 1018 A
Calcoliamo ora il potere risolutivo spettrale teorico del nostro strumento.
Il potere risolutivo teorico R di un reticolo e' definito come R = λ/δ(λ) : dalla teoria del
reticolo R = mN, con m ordine dello spettro ed N numero totale di tratti del reticolo investiti
dal fascio di luce.
Per un reticolo da 600 tr/mm al primo ordine viene R = 15000, ossia 0.3 Angstrom per
λ ~ 5000 A ;
questi 0.3 A corrispondono a 2.6µ sul piano focale del focheggiatore. Nelle condizioni di
seeing suddette (2", ossia 13.7µ) il potere risolutivo dello spettrografo e' dato dalla
proporzione
0.3(A) : 2.6(µ) = x(A) : 13.7(µ)
da cui x=1.6 A
Ma la fenditura e' di 50µ, ben più larga della immagine stellare, quindi il potere risolutivo
spettrale sarà minore di 1.6 A.
Con la fenditura da 50µ ( 30 µ sul piano del focheggiatore ) il potere risolutivo diventa
0.3(A) : 2.6(µ) = x(A) : 30(µ)
da cui x = 3.46 A e quindi R = λ/δ(λ) = 1440, molto minore del 15000 nominale.
Per poter sfruttare il potere risolutivo prima calcolato (R = 1440), occorre che il rivelatore sul
piano focale del focheggiatore abbia una risoluzione adeguata.
La camera CCD MX916 ha i pixel da 11.6µ lungo la dispersione dello spettro.
La fenditura da 50µ sul piano focale del telescopio si proietta in 30µ sul piano dello spettrografo,
che e' circa il triplo degli 11.6µ dei pixel della camera.
Il teorema di Nyquist del campionamento di una funzione dice che il passo di campionamento
deve essere almeno metà della larghezza del profilo da analizzare: il profilo di una riga spettrale e'
quindi campionato in maniera sufficiente per estrarre tutta l'informazione.
Esempi di spettri ottenuti con OMR-10C e camera Apogee
Spettri ottenuti con lo spettrografo OMR-10C e la camera Apogee AP47p (pixel da 13 µ) , fenditura
da 50 µ, reticolo da 600 tr/mm, il 26 maggio 2005.
I tempi di posa sono 1 s per Giove, 60 secondi per Arturo e Denebola, 15 secondi per Regolo. La
scala e' 1.6 Angstrom/pixel.
•
Regolo (Alfa Leonis), tipo spettrale B7 Iab
•
Denebola (Beta Leonis), tipo spettrale A2 V
•
Giove, luce solare riflessa, tipo spettrale G5
•
Arturo (Alfa Bootis), tipo spettrale K2 III
•
P Cygni, tipo spettrale B2pe
Aberrazioni ottiche
L = onda piana in ingresso L1 = onda convergente in uscita L2 = onda convergente ideale
O = obiettivo
dl = scarto tra L1 ed L2
F = fuoco
Definizione:
Il criterio di Rayleigh dice che un sistema ottico e' praticamente perfetto, dal punto di vista delle
aberrazioni, se la differenza d1 tra l'onda reale e quella ideale e' minore di 1/4 della lunghezza
d'onda della luce.
La definizione di Rayleigh e' stata storicamente molto importante in quanto ha permesso di
esprimere in maniera quantitativa le tolleranze di costruzione dei sistemi ottici.
Le aberrazioni di un sistema ottico sono raggruppabili in due classi:
•
•
geometriche
fisiche
Aberrazioni ottiche geometriche
Sferica , Coma , Astigmatismo , Curvatura di campo , Distorsione
Sferica
Una lente semplice
o uno specchio sferico
non mandano allo stesso fuoco i raggi parassiali e marginali di una sorgente posta sull'asse ottico.
Questa aberrazione si chiama pertanto aberrazione SFERICA.
La distanza tra Fp ed Fm e' la misura della aberrazione e varia col quadrato del raggio della lente
(specchio): obiettivi con rapporto focale f/D piccolo hanno quindi una forte aberrazione.
L'aberrazione e' tollerabile se:
ds < 4 x λ x (f/h)²
Quindi, un modo per ridurre l'aberrazione sferica ( e in generale tutte le aberrazioni) e' di
aumentare la focale a parità di diametro dell'obiettivo.
Per correggere l'aberrazione sferica di una lente si deve costruire un doppietto di due lenti con
diversa curvatura.
Le prime realizzazioni si devono a Dollond intorno al 1750.
Per uno specchio sferico l'aberrazione (al primo ordine) e': ds=h^2/(4R) dove R e' il raggio di
curvatura dello specchio (la lunghezza focale e' R/2).
L'aberrazione sferica e' considerata tollerabile se il diametro D e':
D < 0.47 R^(3/4)
con D ed R in millimetri e per lunghezze d'onda di 0.5 micrometri.
Uno specchio parabolico fa convergere in un unico fuoco sia i raggi marginali che quelli parassiali
provenienti dall'infinito, e non ha quindi aberrazione sferica.
Coma
Si presenta quando la sorgente e' fuori dell'asse ottico, ed e' tanto più forte quanto più e' fuori
asse.
La foto della stella doppia Albireo illustra il fenomeno ed e' stata realizzata col TACOR e una
webcam Creative EX Pro: gli specchi del telescopio erano stati appositamente disallineati.
Per comprendere l'origine della coma si può pensare alla immagine di una sorgente puntiforme
(stella) come la somma delle immagini formate da coppie di punti della lente equidistanti dal
centro ma posti lungo un diametro diverso:
ciascuno di essi forma l'immagine in un diverso punto del piano focale e il risultato e' un piccolo
anello.
Corone circolari dell'obiettivo poste a diversa distanza dal centro formano anelli diversi non
concentrici: il risultato e' una specie di cometa luminosa, donde il nome COMA.
1
3
2
4
e
e
e
e
5
7
6
8
in
in
in
in
c
a
d
b
Affinché un obiettivo sia esente da coma occorre che sia h/sin(u) = cost (condizione di Abbe),
dove h e' la distanza dall'asse ottico ed u l'angolo tra l'asse ottico e il raggio convergente al fuoco
passante per h.
Questo viene realizzato costruendo l'obiettivo con due lenti di diversa curvatura e diverso indice di
rifrazione.
Gli obiettivi corretti per la coma si dicono Aplanatici. Tra i riflettori, sono esenti da coma il
Ritchey-Chretien e lo Schmidt.
Astigmatismo
A differenza della coma, che crea immagini asimmetriche, l'astigmatismo crea immagini
simmetriche. Anche questa aberrazione riguarda sorgenti fuori asse. L'immagine di una sorgente
puntiforme creata da un diametro dell'obiettivo e' un bastoncino a una certa distanza focale,
mentre il diametro perpendicolare ne crea un altro a una diversa distanza: a una distanza
intermedia l'immagine e' circolare e diventa sempre più ellittica avvicinandosi alle due immagini
estreme.
L'effetto cresce quanto più si va fuori asse
Distorsione
Anche questa aberrazione riguarda le sorgenti fuori asse. In generale un obiettivo crea una
immagine di una griglia che e' distorta. La distorsione e' schematizzabile in due tipi, a barilotto o a
cuscinetto. La distorsione non modifica la qualità dell'immagine di una sorgente puntiforme, ma
la sua distanza rispetto alle altre sorgenti del campo.
Curvatura di campo
Quando l'astigmatismo e' nullo la superficie di miglior fuoco e' curva.
Un indice della curvatura del piano focale (o curvatura di campo) e' la somma Petzval, che e'
l'inverso del raggio di curvatura.
Questa aberrazione e' importante soprattutto negli oculari, che hanno campi di vista di diverse
decine di gradi per cui la superficie focale non e' più assimilabile ad un piano.
Aberrazioni ottiche fisiche
Risoluzione , Cromatica assiale , Cromatica laterale , vignettatura
Risoluzione angolare
Un obiettivo anche se perfetto non produce una immagine puntiforme di una sorgente puntiforme,
ma una distribuzione di luce determinata dalla diffrazione della luce che lo attraversa.
L'andamento della intensità luminosa in funzione della distanza dal massimo ha un andamento
del tipo (sin(θ)/θ)²
e il diametro del primo minimo e' dato dalla:
θ = 2.44 λ/D (radianti)
dove D e' il diametro dell'obiettivo e λ la lunghezza d'onda della luce, ovvero, in unità lineari sul
piano focale,
d1 = 2.44 λ f/D
dove f e' la lunghezza focale.
Si definisce potere risolutivo di un obiettivo la minima distanza angolare tra due sorgenti
puntiformi (di pari intensità ) che possono essere distinte.
Normalmente si adotta il criterio di Rayleigh (peraltro arbitrario) per cui due sorgenti si dicono
risolte se la loro distanza angolare e'
α = λ /D
Cromatica assiale
Una lente ha un indice di rifrazione che e' diverso per le diverse lunghezze d'onda, per cui la
lunghezza focale e' leggermente diversa per i vari colori. Quindi anche se la sorgente e' in asse si
ha comunque un piano focale diverso per i diversi colori.
Utilizzando due lenti di vetri anche uguali, ma con diversi raggi di curvatura (Dolland 1750), si
possono portare a coincidenza le superfici focali corrispondenti a due colori (es. blu e rosso),
realizzando un obiettivo acromatico; con tre vetri si ottiene l'obiettivo apocromatico che porta a
coincidenza anche il giallo.
Ovviamente la presenza di due o tre lenti viene usata anche per ridurre le altre aberrazioni
geometriche viste prima (Fraunhofer 1820).
Un obiettivo a specchio lavora per riflessione e quindi non ha aberrazione cromatica in quanto la
riflessione non dipende dalla lunghezza d'onda.
Cromatica laterale
Se la sorgente e' fuori asse, la lunghezza focale e' leggermente diversa per le diverse lunghezze
d'onda, per cui una sorgente puntiforme appare leggermente iridata: questa aberrazione si chiama
cromatica laterale o di ingrandimento. Questa aberrazione e' importante soprattutto negli
strumenti a grande campo e negli oculari, che hanno tipicamente campi apparenti di 50°- 70° !
Vignettatura
Il piano focale non e' sempre uniformemente illuminato, e ciò e' vero come al solito tanto più
quanto più il campo angolare dell'obiettivo e' grande.
Di solito l'illuminazione e' massima al centro e diminuisce al bordo. Una variazione del 10% non e'
apprezzabile all'occhio ma e' molto evidente con un moderno rivelatore CCD.
Spettrografi a prisma
Il Prisma, Spettroscopi a prisma,
Prisma obiettivo, Prisma di Amici
Prisma
I primi ad utilizzare il prisma per lo studio della luce emessa dal Sole furono Fraunhofer (1815) e
Wollaston (1818). In particolare Fraunhofer fece la prima catalogazione delle righe dello spettro
solare utilizzando lettere maiuscole e minuscole, a partire dal rosso verso il violetto, catalogazione
tuttora in uso. Pionieri della classificazione spettrale delle stelle furono Padre Angelo Secchi SJ
all'Osservatorio del Collegio Romano (1818-1878), e Sir William Huggins (1824-1910) in
Inghilterra nel suo Osservatorio privato a Tulse Hill.
Righe principali dello spettro solare , Classi spettrali di Harvard , Classificazione MK
Righe principali dello spettro solare
Righe infrarosse (non visibili da Fraunhofer)
8806.7, Mg I
8662.2 + 8542.1 + 8498.1, Ca I
7699.0 + 7664.9, K I
Righe visibili
A: 7594.1, banda atmosferica ossigeno molecolare
B: 6867.5, banda atmosferica ossigeno molecolare
a: 7245.5, banda atmosferica acqua
C: 6562.8, Halfa
D: 5895.9 + 5889.9, Na I
b: 5183.6 + 5172.7 + 5167.3, Mg I
E: 5168.9 + 5167.5, Fe
F: 4861.3 Hbeta,
f: 4340.5 Hgamma,
G: 4307.4 Ca I + 4307.9, Fe
g: 4226.7 Ca I,
h: 4101.7 Hdelta,
H: 3968.5 Ca II,
K: 3933.7 Ca II,
spettro di tipo solare
Tipi spettrali principali
O
B
A
F
G
K
M
Spettro di Altair (tipo A7 fatto col TACOR e grism 207 tr/mm)
Tutti questi studi furono eseguiti utilizzando come mezzo disperdente il prisma.
Il prisma funziona come dispersore della luce perché l'indice di rifrazione del vetro e' diverso per le
varie lunghezze d'onda.
La variazione dell'indice di rifrazione con la lunghezza d'onda e' ben descrivibile con la formula
empirica di Hartmann:
n ~ A+B/(λ-C)
dove le costanti A, B e C sono caratteristiche del vetro utilizzato. A e' un numero puro, B e C sono
espressi in metri nella seguente tabella.
La deviazione della luce rispetto alla direzione di entrata nel prisma varia al variare dell'angolo di
incidenza in maniera non monotona, ma presenta un minimo per una fissata lunghezza d'onda.
Normalmente i prismi lavorano in condizione di deviazione minima perché in questo modo si
minimizzano le aberrazioni ottiche. In questa condizione gli angoli di entrata e di uscita della luce
rispetto alle facce del prisma sono uguali.
La relazione tra indice di rifrazione e deviazione della luce che attraversa il prisma in condizione di
deviazione minima e':
n = n(λ) = sin[(α+δ )/2] / sin(α /2)
dove α e' l'angolo di apertura del prisma, δ la deviazione ed n l'indice di rifrazione rispetto all'aria
alla lunghezza d'onda considerata.
Spettroscopi a Prisma
La struttura classica di uno spettroscopio a prisma e' la seguente: la luce proveniente da una
sorgente viene trasformata in un fascio parallelo da un obiettivo acromatico (detto collimatore),
attraversa il prisma che la disperde e lo spettro risultante viene focalizzato da un altro obiettivo
acromatico (o cannocchiale se si osserva con l'occhio) sul rivelatore. Il prisma viene montato in
modo che la lunghezza d'onda in deviazione minima sia quella centrale dell'intervallo in esame.
Calcoliamo per esempio l'angolo di deviazione per un prisma di 60° di vetro flint alle lunghezze
d'onda di 4000 (n=1.652) e 7000 (n=1.613) Angstrom:
invertendo la formula sù indicata per la misura dell'indice di rifrazione si ottiene:
δ = 2 arcsin (n sin(α /2)) - α
che per α =60 diventa:
per cui:
δ =2 arcsin(n /2)-60
4000 A , δ =51.38°
7000 A, δ =47.52°
tutto lo spettro visibile sta quindi in meno di quattro gradi.
Definizioni:
•
dispersione
D = d(δ)/d(λ)
Se utilizziamo l'espressione di Hartmann per l'indice di rifrazione n:
e ricordiamo la relazione tra δ ed n: δ =2 arcsin (n sin(α /2)) - α
viene, per un prisma di 60° di vetro flint,
d(δ)/d(λ) = -57.3 AB/( λ -C)² ,
n ~ A+B/(λ-C)
°/m
quindi inversamente proporzionale al quadrato della lunghezza d'onda.
•
potere risolutivo cromatico
R = λ/δ (λ)
E' un indicatore della minima differenza di lunghezza d'onda rivelabile.
R = B∗d(n)/d(λ),
dove B e' la lunghezza della base del prisma, assumendo che tutto il prisma sia investito
dal fascio luminoso e d(n)/d(λ) e' la derivata dell'indice di rifrazione rispetto a λ.
Dimostrazione:
i fronti d'onda b e b' sono in fase per definizione, quindi c+c' = nB.
Una diminuzione di λ pari a δ λ, cioè alla nostra risoluzione cromatica, comporta, per il
criterio di Rayleigh, un aumento dell'angolo di deviazione δ = δ c/b (poiché l'indice di
rifrazione e' maggiore il cammino ottico in aria deve crescere).
Questo angolo e' circa λ /b, dove b e' la larghezza del fascio.
Abbiamo perciò c+c'+λ = (n + δ n) B,
da cui viene λ = δ n B.
Dividendo per δ λ e passando al limite si ottiene λ /dλ a = B dn/dλ =R.
La relazione tra angolo di uscita e lunghezza d'onda e' di tipo iperbolico.
Sul piano focale della camera viene descritta con una formula tipo Hartmann, λ = a+b/(xc) dove x e' l'ascissa sul piano focale e a, b, c, sono costanti strumentali determinate dalla
lunghezza focale della camera, l'indice di rifrazione del vetro e l'angolo di apertura del
prisma. Normalmente i coefficienti vengono ricavati sperimentalmente misurando le
posizioni di un certo numero di righe spettrali di lunghezza nota, col metodo dei minimi
quadrati.
Naturalmente per poter sfruttare il potere risolutivo del prisma occorre che l'obiettivo della
camera abbia un potere risolutivo adeguato.
Prisma obiettivo
Il modo più semplice di ottenere uno spettrografo stellare e' di mettere un prisma davanti
all'obiettivo del telescopio. Il prisma ha di solito un angolo piccolo, massimo circa 12°.
I primi esperimenti furono fatti in Italia da Respighi a Bologna e poi da Secchi a Roma,
utilizzando un prisma con angolo di 10° e 16 cm di diametro, davanti a un cannocchiale
acromatico da 22 cm (perduto nel 1958 nell'incendio dell'Osservatorio di Monte Mario).
Questa tecnica non si puo' usare con strumenti di grande apertura per la difficolta' di
realizzare prismi di grandi dimensioni. I prismi obiettivo piu' grandi mai realizzati hanno
un diametro di 134 cm (Tautenburg), 120 cm (Palomar; UK Schmidt), 100 cm (Byurakan;
ESO), 80 cm (Hamburg).
Ovviamente col prisma montato bisogna puntare il telescopio tenendo conto della
deviazione della luce da parte del prisma: poiché l'angolo e' piccolo, δ = (n-1)α , ossia circa
la metà dell'angolo del prisma.
Lo spigolo del prisma viene posto parallelo all'equatore celeste in modo che lo spettro si
disperde in direzione Nord-Sud ed eventuali errori nel moto orario del telescopio allargano
lo spettro perpendicolarmente alla dispersione in lunghezza d'onda, preservando così la
risoluzione spettrale.
Le dispersioni utilizzate in pratica vanno da 200A/mm ad H-gamma, per lavori di
classificazione spettrale MK, a 1800A/mm ad H-gamma per ricerca di oggetti peculiari
(Byurakan survey).
Prisma di Amici
Un modo più economico e' di porre il prisma vicino al piano focale, sul fascio convergente
della luce. Si usa in questo caso il prisma a visione diretta, inventato da Amici (ancora un
italiano).
Si tratta di un sistema di tre (o più) prismi di vetri diversi incollati tra loro e calcolati in
modo che il centro dello spettro in uscita sia parallelo al fascio in ingresso. Poiché il
prisma lavora in condizioni di fascio convergente, anziché parallelo, le aberrazioni ottiche
degradano la qualità dello spettro se lo si usa con telescopi molto aperti (f/D<6).
Sia col prisma obiettivo che col prisma di Amici tutte le stelle presenti nel campo generano
uno spettro sul piano focale del telescopio, per cui questa configurazione e' molto usata
per lavori di "survey".
Il catalogo spettrale HD del 1900 fu fatto col prisma obiettivo, come pure la sua revisione
del 1975 (classificazione MK del Michigan, Houck et al.).
LA CAMERA CCD
Un sensore CCD si può considerare come una matrice bidimensionale di tanti
elementi uguali (pixel) ciascuno dei quali si comporta come un piccolo
condensatore che accumula elettroni in proporzione al numero di fotoni che lo
hanno colpito. Il processo fisico alla base del suo funzionamento si può trovare
nel capitolo 5 delle dispense del Corso di Laboratorio di Astrofisica I (par. 5.1.6),
al quale si rimanda lo studente per l'approfondimento.
Un sensore CCD, anche se non esposto alla luce (otturatore chiuso e tempo di
posa estremamente piccolo, presenta comunque un livello di conteggi maggiore di
zero nei suoi pixel, che dipende dal sensore e dalla elettronica di controllo. Questo
livello si chiama livello di polarizzazione (o bias) e dipende leggermente dalla
temperatura: e' in pratica lo zero effettivo dello strumento e va determinato
sperimentalmente ogni volta che si "accende" la camera, dopo che ha raggiunto la
temperatura di lavoro.
Anche ad otturatore chiuso il sensore accumula comunque una carica nei sui
pixel per effetto della agitazione termica degli elettroni: la carica dipende
esponenzialmente dalla temperatura (tanto minore quanto più la temperatura e'
bassa) e quindi si cerca di far lavorare il CCD alla temperatura più bassa
possibile. Questa carica si chiama corrente di buio e si misura in
elettroni/secondo/pixel: valori tipici sono dell'ordine di 1 o anche meno per i
sensori moderni. Poiché i pixel non sono rigorosamente identici, sia il livello di
bias che di corrente di buio non sono uguali per tutti.
Quando il sensore viene esposto alla luce gli elettroni raccolti sono la somma di
quelli prodotti per effetto fotoelettrico più il bias e la corrente di buio: questi
ultimi vanno quindi sottratti per avere gli elettroni "netti".
Il solo fatto di leggere il sensore produce un errore di lettura (read out noise) che
e' statistico per sua natura e quindi NON può essere tolto.
Riassumiamo le caratteristiche principali di una camera CCD:
•
•
•
•
•
•
dimensioni del sensore
dimensioni dei pixel (tipicamente 20x20 micron per le camere professionali,
5x5 micron per le webcam): la capacità di carica di un pixel dipende dalle
sue dimensioni, più e' grande più elettroni potrà contenere (~300000 per
pixel da 25x25 micron, ~10000 5x5 micron
rumore di lettura (dipende in parte dalla temperatura), dell'ordine di 5-10
elettroni/pixel
corrente di buio, dipende esponenzialmente dalla temperatura, dell'ordine
di 1 elettrone/secondo/pixel
risposta spettrale, tipicamente piccata nel rosso con efficienza quantica fino
all'80 per cento; nell'infrarosso l'efficienza va a zero perché i fotoni non
hanno energia sufficiente a creare una coppia elettrone-lacuna, nel violetto
il sensore e' opaco ai fotoni. Per rendere i sensori CCD sensibili agli
ultravioletti si ricoprono di uno strato di materiale che converte i fotoni UV
in fotoni visibili: dopo un po' di anni il materiale decade e non funziona più.
fattore di conversione tra elettroni e conteggi (GAIN): può andare da circa 1
a 10.
Ci sono due criteri per determinare in fase di costruzione questo fattore.
a) Dividere la capacità del pixel per in massimo numero del convertitore
analogico/digitale usato: per un convertitore a 16 bit questo numero vale
65565.
b) Far corrispondere 1 conteggio al valore rms del rumore del sensore.
Spesso, ma non sempre, i due criteri danno valori simili.
Dal punto di vista della velocità di trasmissione dei dati dalla camera al PC
conviene usare un numero di bit basso (le webcam vanno ad 8 bit), dal
punto di vista della precisione fotometrica conviene un numero di bit alto.
In ogni caso non ha senso "sovracampionare" il rumore: se ho un rumore
rms di 40 elettroni/pixel e' stupido usare un GAIN di 1 e/pixel...
•
tipo di raffreddamento: ad azoto liquido per le camere professionali,
termoelettrico a cella Peltier per quelle amatoriali, ma anche professionali.
Il raffreddamento ad azoto e' tecnicamente molto più complesso ma elimina
quasi completamente la corrente di buio. Il raffreddamento a Peltier e'
molto più semplice ma permette di realizzare una differenza di temperatura
del sensore con l'ambiente di circa 45-50 C. E' possibile usare due stadi di
celle Peltier per realizzare salti termici di 90 C.
Se si scarica il calore in un liquido refrigerante (esempio -10 C) che viene
pompato intorno alla camera, anziché direttamente nell'aria circostante, si
possono ottenere temperature ancora più basse e soprattutto non
dipendenti dalla stagione (in estate l'aria e' molto più calda che in
inverno...).
La riduzione standard di una immagine ottenuta con una camera CCD avviene
dunque secondo lo schema seguente:
•
•
sottrazione della corrente di buio (dark) e della costante di polarizzazione
(bias)
divisione per la immagine di flat-field
La corrente di buio e' prodotta dall'accumulo di cariche elettriche nei pixel della
camera per agitazione termica. Si misura in elettroni/secondo/pixel. Per la DTA a
-30 C e' dell'ordine di 2 e/s/pix.
A questa corrente di buio, che dipende esponenzialmente dalla temperatura
[c = A t exp (-b/T) ]
si aggiunge comunque una costante (bias) che dipende dal sensore e
dall'elettronica di lettura, ed e' la carica accumulata a tempo di posa zero.
Nel caso della DTA questo bias (circa 2900 c/pix) e' disomogeneo sul sensore,
come del resto lo e' la corrente di buio, ma questo fatto non e' critico.
Perché una camera sia utilizzabile per misure di luminosità e' sufficiente che dark
e bias siano riproducibili, anche se diversi da pixel a pixel.
Per poter convertire i conteggi della camera in flusso luminoso occorre conoscere
l'efficienza della camera.
Tre cause concorrono per rendere non banale questa misura:
•
•
•
I pixel di un sensore non rispondono tutti con uguale efficienza alla luce
incidente
Il piano focale del telescopio non e' uniformemente illuminato dall'obiettivo.
Sui telescopi Newton o Cassegrain questo e' dovuto in genere al
sottodimensionamento dello specchio secondario
Luce diffusa, che non segue lo stesso cammino ottico della luce proveniente
dalla sorgente, può cadere sul sensore. Questa luce dipende linearmente
dal tempo di posa, ma può dipendere anche dalla direzione in cui e'
puntato il telescopio ed e' additiva a quella del fondo del cielo.
La correzione alle prime due fonti di disomogeneità si fa illuminando l'obiettivo
con una sorgente estesa uniforme (flat-field) e utilizzando l'immagine così
ottenuta, normalizzata a uno, come divisore dell'immagine astronomica.
Se però c'e' luce diffusa "parassita" questa tecnica non da' buoni risultati: la luce
parassita va identificata e sottratta prima di poter applicare la correzione di flatfield, e non sempre la cosa e' possibile...
Ottenere una illuminazione uniforme non e' facile: una tecnica spesso usata con
piccoli telescopi e' utilizzare la luce del cielo all'alba o al tramonto, quando le
stelle non si vedono più. Tuttavia il cielo ha un gradiente di luminosità anche su
campi piccoli; una ulteriore difficoltà e' posta dal fatto che la luce dei crepuscoli e'
rapidamente variabile, per cui c'e' poco tempo (una decina di minuti) per fare il
flat prima che si vedano le stelle o che la luce saturi il sensore.
Coi grandi telescopi si usa spesso illuminare una stoffa bianca stesa sulla cupola
e puntare su di essa il telescopio: data la breve distanza, la stoffa e'
completamente sfocata e da' una illuminazione uniforme.
Altra tecnica e' inserire una superficie bianca illuminata entro il cammino ottico
del telescopio, che e' così pure sfocata.
Una tecnica molto buona e' il cosiddetto autoflat, ossia usare le stesse immagini
astronomiche per ottenere il flat-field. Se si mediano molte (es. 10) immagini di
campi diversi, in modo che le stelle non capitino sempre sugli stessi pixel, con lo
stesso valor medio del valore di fondo cielo, scartando per ogni pixel il valore più
alto in modo da scartare il caso che sia capitata su quel pixel una stella, si ottiene
la distribuzione di luce sul sensore dovuta al solo fondo cielo.
Ogni manipolazione dei dati di una immagine introduce un rumore che si
aggiunge a quello proprio dell'immagine stessa.
La prima fonte di rumore e' la lettura stessa del sensore. Per la camera DTA
questo rumore di lettura (read out noise o r.o.n.) vale circa 10 e/pix.
La seconda fonte di rumore e' il rumore fotonico Poissoniano, che va con la radice
quadrata degli elettroni rivelati.
La terza fonte di rumore e' la dark+bias, che viene comunque accumulata dal
rivelatore durante la posa: la componente dark può essere considerata
Poissoniana e il suo rumore cresce con la radice del tempo di posa, mentre il
rumore del bias e' costante.
Una quarta fonte di rumore e' la correzione stessa di flat-field. Normalmente le
disomogeneità di risposta dei singoli pixel sono di pochi percento, quindi il flat
field deve avere un rumore per pixel minore dell'uno per mille per non introdurre
un errore apprezzabile. Questo comporta livelli di conteggio molto alti, e la media
di un grande numero di immagini prese tutte in condizioni costanti di
illuminazione.
Il flat sul cielo di solito riproduce molto bene la variazione di illuminazione del
piano focale ma non ha statistica sufficiente per determinare la variazione di
efficienza da pixel a pixel; il flat artificiale va bene per quest'ultimo scopo ma può
avere una distribuzione di illuminazione a grande scala sistematicamente diversa
da quella della immagine astronomica ...
Si possono usare entrambe le tecniche di flat-field per misure di grande
precisione.
Spettroscopio a prisma
Lo spettroscopio mostrato in Figura è costituito da tre parti: il collimatore (Coll.), la piattaforma (P)
e il cannocchiale (Cann.).
Il collimatore è formato da una fenditura regolabile (F) e da una lente (L1), regolata in modo tale da
rendere parallelo il fascio di luce trasmesso attraverso F.
La piattaforma è regolabile in altezza, può girare attorno all'asse verticale passante per O e può
essere resa perfettamente orizzontale agendo sulle tre viti, 1, 2 e 3, poste a 120°.
Il cannocchiale, dotato di oculare (Ω), può ruotare attorno ad O solidalmente o indipendentemente
dalla piattaforma.
La scala graduata su cui effettuare le letture angolari ruota insieme al cannocchiale. L'angolo può
essere letto su due posizioni diametralmente simmetriche dotate di nonio che permettono una
sensibilità di 1'. I due noni servono per eliminare l'errore sistematico prodotto dalla eventuale
eccentricità della scala graduata rispetto all'asse meccanico di rotazione del cannocchiale.
Leggendo ogni posizione angolare del cannocchiale utilizzando entrambi i noni, il valore
dell'angolo si ottiene dalla media dei due valori.
Operazioni preliminari
1) Regolare il cannocchiale in modo che metta a fuoco all'infinito: in pratica, non essendoci
finestre nel laboratorio per guardare fuori, mettere a fuoco il più lontano possibile, usando magari
il corridoio del laboratorio.
2) Posizionare la sorgente S (per esempio la lampada al Sodio, Na) davanti a F. Questa deve essere
stretta, ma non troppo, e deve trovarsi nel piano focale di L1. Per fare questo controllare che il
fascio di luce proveniente da F risulti a fuoco nel cannocchiale. Se non e' a fuoco regolare la
posizione della fenditura F tramite l'apposita vite. A questo punto regolare l'apertura di F al
minimo consentito e assicurarsi che sia verticale.
3) L'asse ottico del collimatore e del cannocchiale devono coincidere quando θ = 0°. In questo caso
la lettura della posizione angolare fatta con i due noni dà l'angolo di riferimento o di zero.
4) Collocare il prisma sulla piattaforma P con lo spigolo verticale e la base parallela all'asse ottico
del collimatore; regolarla in altezza in modo che il prisma sia allo stesso livello del collimatore.
5) Ruotare il cannocchiale di un angolo circa 50° rispetto all'asse ottico del collimatore.
6) Ruotare il prisma, mandando lo spigolo verso il cannocchiale, fino a che lo spettro della
lampada entra nel campo di vista del cannocchiale. Livellare eventualmente la piattaforma in
modo che le righe dello spettro siano verticali.
7) Concentrare l'attenzione sulla riga gialla (doppietto) e notare come, ruotando lentamente il
prisma e lasciando fermo il cannocchiale, la riga si sposta prima in un verso e dopo in verso
opposto. Il punto in cui avviene l'inversione corrisponde all'angolo di deviazione minima per la riga
in esame.
Bloccare la piattaforma in questa posizione.
Conduzione dell'esperienza con il prisma
Lo scopo di questa esperienza è duplice:
A) tarare in lunghezza d'onda lo spettroscopio, ossia costruire una tabella dell'angolo di
deviazione θ in funzione di λ .
B) misurare alcune lunghezze d'onda incognite
A) Utilizzare sia la lampada al Sodio che quella al Mercurio in modo da avere un buon numero di
righe su cui costruire il grafico di taratura.
Per ogni riga spettrale nota misurare l'angolo di deviazione, lasciando fermo il prisma sulla
posizione di deviazione minima del giallo determinata in precedenza.
Riportare su grafico in ascissa sin(θ) e in ordinata λ e ricavare i valori dei coefficienti del
polinomio che meglio li approssima (provare con vari gradi) e fare il relativo grafico con una scala
che lo renda utilizzabile.
B) Effettuare le misure di posizione di tutte le righe visibili per le quali non sia data la lunghezza
d'onda nella tabella in dotazione. Ricavare la loro lunghezza d'onda dalla curva di taratura
ottenuta al punto A.
Stima dell'errore
L'errore per ciascuna riga può essere valutato calcolando i valori di lambda corrispondenti agli
estremi dell'intervallo di confidenza dell'angolo di deviazione misurato.
DIFFRAZIONE DA PARTE DI UNA FENDITURA
L'esperienza consiste nello studio della diffrazione di Fraunhofer di un fascio laser da una
fenditura lineare o da un'apertura circolare (pin-hole). E' possibile misurare con la diffrazione la
dimensione della fenditura. Questa si può ricavare sfruttando le note relazioni:
sin(θ) = m λ/b
sin(θ) = 1.22 m λ/d
che valgono rispettivamente per una fenditura lineare di larghezza b e una apertura circolare di
diametro d.
In queste equazioni m rappresenta l'ordine di diffrazione. Per m = 1, θ corrisponde all'angolo del
primo minimo di diffrazione. Riportando nei due casi sin(θ) in funzione di m (tipicamente da -2 a
2), è possibile ricavare il valore di b (ovvero d) dal coefficiente angolare della funzione così
linearizzata.
La misura di θ richiede la conoscenza della distanza x del primo minimo dal massimo centrale.
Vale infatti la relazione tan(θ)=x/L, dove L è la distanza tra la fenditura e il fotodiodo e x
corrisponde allo spostamento trasversale del fotodiodo rispetto al massimo centrale di diffrazione.
Per piccoli valori di x, possiamo porre tg(θ) = θ.
Conduzione dell'esperienza:
Sono disponibili fenditure da 0.2, 0.3 e 0.4 mm e pin-holes di diametro pari a
0.1, 0.2, 0.3 e 0.6 mm, montati all'interno di un apposito sostegno. E' lecito
riportare sullo stesso grafico i dati relativi alle fenditure e ai pin-holes, purchè
si moltiplichi l'inverso del diametro per il fattore 1.22 che è dovuto alla
presenza della funzione di Bessel J0 nella funzione di diffrazione da
un'apertura circolare.
Al fine di avere una buona risoluzione spaziale della figura di diffrazione è bene
condurre l'esperienza con grandi valori di L (almeno 50 cm). Inoltre va
considerato che la regione attiva del fotodiodo è limitata spazialmente da un
foro di 200 micron di diametro. Benché la sensibilità della slitta micrometrica
su cui è montato il fotodiodo sia di 10 micron si consiglia di non effettuare
spostamenti minori di 100 µ.
Prima di iniziare le misure bisogna controllare che l'apparato sia allineato
correttamente. Lo specchio M va posto a 45° rispetto alla direzione del fascio
incidente. Agendo sulle due movimentazioni di M (orizzontale e verticale) si
deve far sì che il fascio riflesso da M viaggi orizzontale. Utilizzando uno dei pinholes controllare che il fascio incida esattamente al centro: questo si può fare
controllando che la figura di diffrazione del foro sia simmetrica.
L'esperienza consiste di tre parti:
•
•
•
misura della larghezza b di una fenditura . Si richiede di confrontare il valore di b ottenuto
dall'esperimento con quello nominale inciso sul barilotto della fenditura utilizzata.
misura del diametro d di un foro . Si richiede di confrontare il valore di d ottenuto
dall'esperimento con quello nominale inciso sul barilotto del foro utilizzato.
ricostruzione della figura completa di diffrazione ottenuta in uno dei due casi precedenti e
confronto mediante test del Χ2 con la funzione aspettata
I(s)=IM[sin2(s)/s2]
dove s = 3.14159 b sin(θ)/λ e IM rappresenta il valore di I per θ = 0 (massimo centrale).
Nel nostro caso al posto di sin(θ) possiamo mettere x/L, se x e' la distanza dal centro della
figura di diffrazione.
Se l'allineamento della fenditura non è perfetto è possibile che la figura di diffrazione
risulti lievemente asimmetrica rispetto al massimo centrale. Tale asimmetria comporta che
il valore della larghezza della fenditura ricavata dai dati presi a destra sia diversa da quella
ricavata dai dati a sinistra del massimo centrale. In questo caso conviene misurare la
posizione di entrambi i minimi laterali del primo ordine e poi farne la media per conoscere
θ.
Poiché la funzione I(s) e' simmetrica, il test del Χ2 darà un cattivo risultato se la figura di
diffrazione reale non e' simmetrica. In questo caso conviene lasciare i parametri della
funzione (posizione del centro della figura di diffrazione, larghezza della fenditura, intensità
centrale) come parametri liberi, ottenere i loro valori col metodo dei minimi quadrati e
infine fare il test del Χ2 utilizzando questi valori. In questo caso al posto di sin(θ) nella
funzione dobbiamo mettere (x-x0)/L dove x0 sarà l'ascissa del centro della figura e x la
posizione del fotodiodo.
Suggerimenti pratici
- Allineare il fascio di luce del laser con il foro del fotodiodo curando che lo stesso sia a metà della
corsa del carrello mobile.
- Evitare di tenere a lungo il fotodiodo centrato sul massimo della figura di diffrazione.
- Per evitare che il fotodiodo vada in saturazione (~20 Volt) in prossimità del massimo, rendendo
così impossibile la determinazione della posizione dello stesso, e' bene attenuare l'intensità del
fascio laser sia limitandone il diametro all'origine con l'apposito diaframma posto a breve distanza
dal laser, sia con gli appositi filtri (vetrini anneriti o filtri Polaroid) da collocare a monte della
fenditura usando gli appositi sostegni.
-controllare che l'alimentatore del fotodiodo dia la giusta tensione.
-eseguire le misure con una certa rapidità per evitare eventuali effetti di deriva del fotodiodo.
-verificare se la luce diffusa della stanza produce una tensione di uscita non nulla anche se la
luce del laser non cade sul fotodiodo. Tale valore andrà ovviamente sottratto dal valore letto per
fare il fit con la funzione aspettata e il calcolo del Χ2.
Si ricorda che la variabile Χ2 per un insieme di dati sperimentali descrivibili con una funzione F e'
definita come la sommatoria, su tutti i punti sperimentali, dei rapporti
( Foss-Fcalc )2/σ2,
dove σ e' l'errore attribuito a ciascun dato. L'errore formale può essere ricavato dal libretto
istruzioni del multimetro usato per leggere la tensione di uscita del fotodiodo, ma l'errore effettivo
può essere maggiore: un buon modo per valutarlo e' compiere misure ripetute della tensione
spostando il fotodiodo di più di 200 µ (diametro del foro di ingresso) e riportandolo nella posizione
voluta.
Un buon fit ha un Χ2 dell'ordine del numero di punti sperimentali meno i parametri liberi.
E' in ogni caso istruttivo ricavare i valori dei parametri della funzione (posizione del centro della
figura di diffrazione, larghezza della fenditura, intensità centrale) dal fit della funzione con
l'insieme dei dati sperimentali e vedere quanto si discostano da quelli ricavati dalle sole posizioni
dei massimi e minimi.
Sia il metodo dei minimi quadrati che il test del Χ2 valgono nel caso di dati statisticamente
indipendenti: poiché il fotodiodo ha un foro di accettazione di 200 µ, misure più ravvicinate NON
sono indipendenti e quindi non possono essere usate.
Ha però senso fare misure a passi di 100 µ per la ricerca manuale delle posizioni dei massimi e
dei minimi della figura di diffrazione.
Classificazione spettrale
I primi ad utilizzare la spettroscopia per lo studio della luce emessa dal Sole furono Fraunhofer
(1815) e Wollaston (1818). In particolare Fraunhofer fece la prima catalogazione delle righe dello
spettro solare utilizzando lettere maiuscole e minuscole, a partire dal rosso verso il violetto,
catalogazione tuttora in uso.
Pionieri della classificazione spettrale delle stelle furono Padre Angelo Secchi SJ, all'Osservatorio
del Collegio Romano (1818-1878), e Sir William Huggins (1824-1910) in Inghilterra, nel suo
Osservatorio privato a Tulse Hill.
All'inizio del 1900 venne realizzato il catalogo spettroscopico Henry Draper (HD), con la nota
sequenza dei tipi spettrali O, B, A, F, G, K, M ( classificazione di Harvard ), sotto la direzione di
E.Ch. Pickering e il contributo fondamentale di tre donne, W.P. Fleming, A.C. Maury e A.J.
Cannon. Il catalogo HD e' tuttora un riferimento storico fondamentale.
Poco dopo il 1940 venne fatta una nuova classificazione spettrale ad opera di Morgan e Keenan
(sistema MK), introducendo la classe di luminosità oltre al tipo spettrale: questa classificazione e'
quella attualmente più usata.
•
•
•
Classificazione delle stelle nel sistema MK
Classificazione delle nane di bassa sequenza principale
Tabelle di righe spettrali stellari e di lampada
Guide di luce
Guide di luce , Spettroscopia multioggetto, Spettrografi echelle
Guide di luce
Una fibra ottica e' un filo sottile (da 500 a 50 micron di diametro) di materiale trasparente,
ricoperto da una guaina di plastica o di vetro con indice di rifrazione sensibilmente minore.
La fibra ottica funziona sul principio della riflessione totale: la luce che entra nella fibra con un
angolo, rispetto all'asse, minore di un certo limite viene totalmente riflesso all'interfaccia
nocciolo/rivestimento e si propaga con riflessioni successive fino all'altro capo della fibra,
praticamente senza perdite. L'angolo limite e' θ =arcsin(n2/n1), dove n2 e' l'indice di rifrazione del
materiale esterno ed n1 quello interno.
L'angolo di accettazione e' dato dalla relazione:
sin(α ) = {SQRT [ (n1)² - (n2)² ] } / n0
dove n0 e' l'indice di rifrazione del mezzo esterno.
Il grande vantaggio della fibra ottica e' che può essere curvata senza problemi, purché il raggio di
curvatura sia grande rispetto al diametro della fibra, e quindi si può collegare un estremo al
telescopio, libero di puntare qualunque direzione in cielo, mentre l'altro estremo porta la luce allo
spettrografo collocato fisso su un tavolo.
Le perdite di trasmissione della luce sono difficili da calcolare a priori. In pratica ogni fibra si
comporta diversamente e l'efficienza va misurata a posteriori. Una lunghezza di uno o due metri
produce assorbimenti ancora tollerabili. Le facce di ingresso e di uscita della fibra devono essere
lavorate piane con estrema precisione per ridurre le perdite di luce.
L'apertura numerica NA = sin(α ) e' legata all' F/# dalla relazione
F/# = 1/(2 NA)
La tabella seguente da' l'apertura numerica, il rapporto focale equivalente e l'angolo di ingresso
per alcune fibre ottiche tipiche.
Nocciolo Rivestimento
Silice
Silice
Liquido
Vetro
Plastica
Silice
Plastica
Vetro
F/#
NA
1.9
2.3
1.1
0.9
0.27
0.22
0.47
0.56
Cono di ingresso (°)
31
25
56
68
Per massimizzare l'efficienza, l'angolo di accettazione della fibra deve essere abbastanza grande da
prendere tutta la luce raccolta dal telescopio: questo in genere non e' un problema dato che i
telescopi hanno tipicamente valori F/5 - F/10.
Il problema viene all'uscita, dove il cono di luce deve essere abbastanza stretto da entrare nella
fenditura dello spettrografo. Se il cono di uscita e' troppo largo si perde una parte della luce
raccolta e anche si può avere luce diffusa nello spettrografo. La soluzione migliore e' di usare un
fascio di fibre ottiche circolare dal lato del telescopio e lineare dal lato spettrografo. Il fascio di
fibre può costituire esso stesso la fenditura di ingresso, o essere appoggiato alla fenditura.
Una guida di luce può essere preferibile all'accoppiamento ottico diretto tra telescopio e
spettrografo in due casi:
•
•
spettrografo troppo pesante per essere attaccato al telescopio
spettroscopia simultanea di molti oggetti (o di diversi punti di un oggetto esteso) nel campo
del telescopio.
Uno spettrografo deve essere meccanicamente molto rigido in modo da mantenere le ottiche
allineate qualunque sia la sua orientazione. Deve inoltre essere stabile dal punto di vista termico,
dato che la scala delle lunghezze d'onda dipende dalla lunghezza focale del focheggiatore, mentre
il potere risolutivo dipende anche dal rapporto tra le focali del collimatore e del focheggiatore.
Spettrografi di alta risoluzione tendono quindi ad essere molto pesanti: si preferisce perciò non
applicarli al fuoco Cassegrain di un telescopio, ma al fuoco Nasmith o coude'.
Nel caso di un telescopio piccolo il peso dello spettrografo e relativa camera può essere
relativamente molto grande: se il telescopio non ha un fuoco Nasmith o coude' l'unico metodo per
accoppiare otticamente il telescopio e lo spettrografo e' di usare una fibra ottica.
Spettroscopia multioggetto
Lo spettroscopio a fenditura produce sul piano focale una immagine bidimensionale: una
dimensione e' la lunghezza d'onda, l'altra e' l'ascissa lungo la fenditura. In pratica si può
schematizzare l'immagine come se fosse formata da tante immagini adiacenti della fenditura,
larghe quanto la risoluzione cromatica. L'immagine spettrale di una stella posta al centro della
fenditura e' un rettangolo, alto quanto la fenditura, con una striscia luminosa nella posizione
della stella alta quanto l'immagine della stella, e due rettangoli adiacenti con lo spettro del cielo.
Ovviamente lo spettro del cielo e' presente anche nella striscia della stella e va sottratto per avere
lo spettro netto della stella.
Se sulla fenditura cadono più stelle, ciascuna di esse produrrà una striscia corrispondente al
proprio spettro, ovviamente tanto più luminosa quanto più la stella e' brillante.
Con uno spettrografo a fenditura si può quindi ottenere lo spettro di una stella per volta, o due
molto vicine. Ma poiché il campo osservato dal telescopio e' un'area di cielo molto maggiore
dell'area della fenditura, si pone il problema di ottimizzare l'uso del tempo di osservazione per
ottenere simultaneamente lo spettro di tutte le (o di molte delle) stelle del campo.
Una soluzione e' quella di abolire la fenditura, come nel caso del prisma obiettivo o del prisma di
Amici. In questo caso però la risoluzione spettrale e' comunque bassa (R~100) e non e' uguale per
tutte le osservazioni, ma dipende dalle condizioni atmosferiche e dalla precisione della guida in
declinazione.
Volendo mantenere il vantaggio di una risoluzione medio-alta (R~1000-5000) e costante si deve
usare la fenditura: esistono due soluzioni, entrambe usate in pratica.
•
Portare le immagini di tutte le stelle del campo, di cui si vuole ottenere lo spettro, allineate
una accanto all'altra sulla fenditura dello spettrografo tramite fibre ottiche (una per
ciascuna stella) mobili sul piano focale del telescopio, azionate da bracci robotici;
•
Costruire una piastra da mettere sul piano focale con piccoli fori in corrispondenza delle
stelle da osservare, a ciascuno dei quali attaccare una fibra ottica che porta l'immagine
sulla fenditura dello spettrografo.
Il primo metodo richiede una struttura molto complessa e pesante da collocare sul piano focale;
ha il vantaggio di essere utilizzabile per qualunque campo, ma limiti meccanici dei bracci
posizionatori delle fibre pongono dei vincoli sulle distanze tra gli oggetti da osservare .
Il secondo richiede di realizzare, con elevata precisione, una piastra per ciascun campo stellare si
voglia analizzare, con piccoli fori in corrispondenza di ciascuna stella; in pratica bisogna fare una
immagine diretta del campo col telescopio su cui si monterà lo spettrografo qualche giorno prima
e utilizzarla per definire le posizioni relative delle stelle, in modo da tenere conto di tutte le
distorsioni geometriche sul piano focale dello strumento.
Il collegamento delle fibre alla piastra va fatto a mano. Il vantaggio e' di avere una struttura
leggera e di poter fare spettri di sorgenti anche molto vicine tra loro e in numero molto maggiore
del sistema robotico.
Spettrografi eccelle
Per la spettroscopia ad alta risoluzione si usavano in passato spettrografi posti al fuoco coude' dei
grandi telescopi equatoriali. Questi spettrografi erano collocati al piano sotto la cupola, in una
stanza termostatata che garantiva le necessarie condizioni di stabilità termica e quindi di
invarianza degli allineamenti delle ottiche e della scala sul piano focale, in modo da permettere
misure accurate di velocità radiali (minori di 1 km/s).
Le elevate dispersioni ottenibili con questi strumenti (fino a 3 A/mm) comportavano l'uso di lastre
fotografiche lunghe decine di centimetri per coprire un intervallo di soli 1000 A.
Con l'avvento degli intensificatori di immagine elettronici, con sensori di forma rotonda o quadrata
di pochi centimetri di lato, questi spettrografi non permettevano più di registrare porzioni
significative di spettri, e si pose il problema di ottimizzare l'uso del tempo di osservazione.
Venne così realizzato lo spettrografo "echelle"
Il principio su cui si fonda lo spettrografo echelle e' il seguente:
se riprendiamo l'equazione del potere risolutivo del reticolo,
R = Nm = (L/p)m,
dove p e' il passo del reticolo, L la sua lunghezza ed m l'ordine dello spettro, si vede che per
ottenere elevata risoluzione si può pensare di usare uno spettro di ordine elevato, anziché
aumentare la densità dei tratti. Di fatto la densità dei tratti non può essere molto maggiore di
2400 tr/mm, e per avere risoluzioni di ~100000 al primo ordine occorrono reticoli di 10 cm.
Dalla equazione fondamentale del reticolo:
p sin(θ ) = mλ,
viene che già al secondo ordine lo spettro non e' "pulito" ma c'e' sovrapposizione degli ordini per
densità di 1000 tr/mm.
Se si usa un reticolo con bassa densità di tratti (~30 tr/mm) e lo si usa all'ordine 30 si ha per
λ=5000 A e λ=6000 A,
m
30
31
32
33
θ
27.035
28.014
29.002
30.000
33.056
34.307
35.578
36.870
ossia tutti gli ordini sono praticamente sovrapposti. Se però interponiamo, sul fascio in uscita dal
reticolo, un secondo reticolo con i tratti disposti ortogonali al primo (o un prisma con lo spigolo
ortogonale ai tratti del primo) i diversi ordini si trovano leggermente spostati uno sotto l'altro,
anziché sovrapposti. Così lo spettro, invece di essere disposto su una lunga linea, si trova
suddiviso in tanti segmenti paralleli che coprono una area rettangolare e possono essere registrati
da un sensore di forma adeguata.
Nel calcolo di uno spettrografo echelle bisogna fare in modo che ciascun segmento di spettro
includa un piccolo intervallo di lambda del segmento precedente, in modo da non avere buchi
nella copertura dello spettro.
Gli ordini di uno spettro echelle sono generalmente leggermente curvi, e le righe spettrali non
sono ortogonali alla dispersione, per cui l'analisi dei dati e' sensibilmente più complessa di uno
spettro normale. Esiste inoltre molto spesso un problema di luce diffusa, riflessi e disuniformità di
illuminazione, per cui la calibrazione in flusso e' molto più problematica.
Gli spettrografi echelle sono usati sia per telescopi a terra che per telescopi nello spazio (es. IUE)
La tabella seguente riporta i dati dello spettrografo CASPEC usato al fuoco Cassegrain del
telescopio da 3.6m dell'ESO.
Table 1.1: 3.6m + CASPEC characteristics
CASPEC SPECTROGRAPH
Quantity
guide probe
slit viewer field
value
comment
1'x1.3'
0.312 arcsec/mm
1.5'x2.5'
0.39 arcsec/pixel
limiting magnitude
in thè slit viewer
~21
slit orientation
scale at the slit
max. slit length
slit width (a)
east-west
7.12 "/mm
20 mm (142.4 arcsec)
70 micron - 2 mm
0.5" < (a) < 14.2"
grating constant
(nxlambda)
56770
recipr. linear disp. (nm/mm)
Rmax with CCD #37
available range
spectral coverage
interorder separation
lambda/1991
41000
2 pixel sampling
310-1100 nm
240 nm
0.55 -1.4 mm
23 - 58 pixels
no full order overlap
for lambda > 710 nm
BLUE CROSSDISPERSER
spectral coverage
interorder separation
120 nm
0.43-1.5 mm
13-62 pixels
CCD DETECTOR
Scale I] dispersion
Scale -L dispersion
0.49 arcsec/pixel
20.4" /mm
0.33 arcsec/pixel
13.75 /mm
24 micron pixel
OBSERVING MODES
• Standard mode: echelle + RED (BLUE) Crossdisperser
• Zeeman: echelle + BLUE Crossdisperser + Zeeman analyser
• Long Slit: echelle + mirror + filter (only one order recorded)
Quest' altra tabella da' le caratteristiche dello spettrografo echelle a bordo del satellite ultravioletto
IUE (International Ultraviolet Explorer che ha operato per circa 20 anni (1978-98), il più longevo
dei satelliti scientifici in orbita terrestre.
Table 10.6 Parameters of the IUE spectroscopes
Entrance aperture
100 micron circular or 330 x 660 micron elliptical
(3" or 10" x 20" on the sky)
Collimators
Each off-axis paraboloids of focal length 1.89 m
Gratings
Short wavelength echelle grating; 102 lines per mm covering
the range 115-195 nm over spectral orders 66 to 125 at a
dispersion ranging from 0.086 to 0.137 nm/mm, and a
spectral resolution of 12000. The spherical grating used as
a cross disperser has 313 lines per mm, and a focal length
of 0.69 m.
Long wavelength echelle grating; 63 lines per mm covering
the range 190-320 nm over spectral orders 72 to 125 at a
dispersion ranging from 0.125 to 0.2 nm/mm, and a spectral
resolution of 13000. The spherical grating used as a cross
disperser has 200 lines per mm, and a focal length of 0.69 m.
In both spectroscopes a piane mirror can be inserted in front
of the echelle grating, leaving the cross disperser as the only
dispersing element and giving a low dispersion mode to the
system. The dispersions and spectral resolutions are then
respectively 6 nm/mm and 250 for the short wavelength
spectroscope, and 6 nm/mm and 300 for the long wavelength
spectroscope
Detectors
Throughput
An UV-optical converter followed by an SEC-vidicon
television camera
About 2% for the short wavelength spectroscope and from
0.45% to 4% for the long wavelength spectroscope (including
the losses in the telescope)
Anche strumenti come il BFOSC possono lavorare in modalità echelle, mettendo il reticolo echelle
nella prima ruota e il cross disperser nella seconda, anche se non sono così efficienti come uno
spettrografo echelle vero e proprio.
Analisi di spettri acquisiti col TACOR
Scopi dell'esperienza:
1) Estrarre gli spettri dalle immagini bidimensionali.
2) Calibrare gli spettri in lunghezza d'onda.
3) Valutare il potere risolutivo dell'apparato strumentale usato (telescopio +
spettrografo + camera CCD).
4) Misurare le larghezze equivalenti (E.W.) e le larghezze a metà altezza (FWHM) di
righe stellari.
5) Studiare la variazione della larghezza equivalente delle righe della serie di
Balmer al variare del tipo spettrale.
6) Verificare la classificazione spettrale delle stelle osservate.
Introduzione al sistema di analisi dati
I dati acquisiti col calcolatore di controllo del TACOR vengono trasferiti via rete
sul server astro1.phys.uniroma1.it. A ciascuna notte di osservazione corrisponde
una cartella e i file contenuti sono accessibili tramite un browser di rete dalla
pagina
http://astro1.phys.uniroma1.it/nesci/nesci.html
Ciascun gruppo utilizza uno dei PC del Laboratorio, denominati e3pcnn (con nn
da 01 a 10) operanti sotto Windows 98SE.
Ecco la serie di comandi da dare:
entrare sul proprio PC dando come username e password il nome del PC stesso
(tutte minuscole);
sul disco F (studenti) creare una cartella col nome del proprio gruppo. Questa
operazione va ovviamente fatta solo la prima volta: in questa cartella saranno
immagazzinate le immagini del TACOR, gli spettri che verranno estratti durante le
esercitazioni e i risultati dei fogli di lavoro.
Sono disponibili ORIGIN, KALEIDAGRAPH e STAROFFICE (versione SUN di
Microsoft Excel).
Negli appunti saranno date indicazioni operative per il software Kaleidagraph, ma
voi siete liberi di usare quello che preferite.
Le cartelle saranno mantenute sui PC fino alla fine del Corso (e degli esami
relativi).
Riduzione delle immagini
La prima cosa da fare e' scaricare le immagini desiderate da astro1 sul vostro PC.
Le immagini sono in formato FITS: usate il tasto destro del mouse cliccando sul
nome del file prescelto e salvatelo sulla vostra cartella dati. Per iniziare conviene
usare i dati fatti da voi, ma poi potete usare i dati di tutti.
Se nella notte sono state fatte le immagini di DARK e BIAS scaricatele tutte.
Visualizzazione delle immagini
Per visualizzare le immagini usate MaximDL. Questo programma serve anche per
calcolare la DARK e il BIAS medio, sottrarli dalle immagini astronomiche ed
estrarre gli spettri.
Sottrazione del BIAS
Aprire un certo numero (almeno 3) di immagini di BIAS, selezionare Process Combine; caricare le immagini da mediare, selezionare Median, Align=none,
Overlay All Images. Dare OK e salvare l'immagine ottenuta col nome proposto o
con uno più adatto. Più numerose sono le immagini mediate, più basso sarà il
rumore della immagine risultato: se l'origine del rumore e' casuale, il rumore
diminuisce proporzionalmente alla radice quadrata del numero di immagini.
Per sottrarre il BIAS ad una immagine bisogna che sia stato ottenuto alla stessa
temperatura (la temperatura e' registrata nella Header di ogni immagine). La
sottrazione si fa dal menu Process - Pixel Math. Dare il nome della immagine
grezza, selezionare subtract e il nome della immagine di BIAS. Poiché i dati sono
trattati come interi senza segno (da 0 a 65565) MaximDL non sa trattare i numeri
negativi: aggiungere quindi una costante (es. 200) in modo che i pixel che
diventassero negativi siano ancora rappresentabili: i pixel a zero ora varranno
200. Questo permette di vedere non solo che il valore aspettato dove non c'e'
segnale e' fluttuante intorno allo zero (200) ma anche di vedere le fluttuazioni e
misurarle, con la finestra View - Information window (tasto rapido mirino).
Se si fa la differenza tra un BIAS e il BIAS medio e si guarda la fluttuazione dei
dati all'interno di un'area selezionata (almeno 10x10 pixel) si ottiene una stima
del Read Out Noise (dell'ordine di 3 conteggi/pixel per la DTA). Questo errore e' il
minimo possibile per la camera in uso.
Oltre al BIAS nella camera CCD si accumula la carica di corrente di buio, che e'
proporzionale al tempo di posa. Per avere i conteggi netti si deve quindi sottrarre
non solo il BIAS ma anche la corrente suddetta. Occorre quindi ottenere alcune
immagini prese ad otturatore chiuso, con lo stesso tempo di posa delle immagini
astronomiche e mediare come si e' fatto per le immagini di BIAS. Ovviamente
queste immagini sono la somma del BIAS e della DARK, quindi basta sottrarre
questa immagine media a quella astronomica per avere i conteggi netti.
Se si sono fatte immagini con diversi tempi di posa non occorre fare DARK medie
per ogni tempo di posa usato. Basta sottrarre il BIAS dalla DARK media da 1
minuto e avere così la corrente di buio netta. Poi si moltiplica questa immagine
per il numero di minuti di posa dell'immagine, si aggiunge il BIAS medio e si
ottiene una DARK del tempo di posa desiderato. La DARK dipende
esponenzialmente dalla temperatura: a -30 e' circa 1 conteggio/secondo/pixel per
la camera DTA.
Togliere il BIAS e la DARK serve per poter fare misure di flusso luminoso, per le
quali servono i conteggi netti.
Da questo punto di vista una misura di larghezza equivalente E' una misura di
flusso, sia pure relativo, e quindi prevede la sottrazione della corrente di buio e
del BIAS.
Serve però anche da un punto di vista puramente estetico soprattutto se il BIAS e
la DARK non sono uniformi sul sensore, come e' il caso di diversi sensori che
mostrano gradienti o strutture periodiche nel BIAS.
Estrazione degli spettri
Dopo avere, se del caso, sottratto BIAS e DARK, si possono estrarre gli spettri con
MaximDL dal menu View - Line profile:
selezionare "vertical box" e definire un rettangolo ALTO QUANTO IL CCD e il più
stretto possibile, che includa tutto lo spessore della stella. Nella toolbox appare lo
spettro estratto: accertarsi che il valore graficato sia la media lungo la riga dei
conteggi, dai bottoni di selezione a lato. Il grafico si salva (casella export) in
formato csv: dare un nome che sia legato al nome della stella. Questo file e' un file
testo che si può leggere con Excel - Origin - Kaleidagraph per la successiva
analisi.
Ovviamente, se si desidera conoscere il valore dei conteggi effettivi dello spettro
sul sensore bisognerà moltiplicare il valore medio così ottenuto per la larghezza
del "box" usato per l'estrazione.
Calibrazione in lunghezza d'onda
Scegliere una stella di tipo spettrale caldo (B o A) in cui sia evidente la serie di
Balmer dell'Idrogeno.
Identificare i minimi di intensità delle righe (dal grafico o dalla tabella numerica) e
creare una nuova tabella con le lunghezze d'onda in una colonna e le posizioni in
pixel dei minimi nell'altra. Farne il grafico e verificare a occhio che la correlazione
sia approssimativamente lineare e che quindi non sono stati commessi errori
grossolani nel prendere le posizioni delle righe.
Ricavare i coefficienti della relazione λ = a+bx col reticolo da 600 tratti/mm e la
camera DTA (24 micron/pixel) la corrispondenza e' circa 3 A/pixel.
Se lo scarto quadratico medio e' troppo grande (più di un pixel ovvero più di 3
Angstrom) verificare che non ci siano errori nei dati utilizzati.
Una volta trovata la relazione per la stella di riferimento la si può applicare a tutte
le stelle usando il foglio elettronico in uso. Questo e' vero a patto che la finestra di
estrazione sia la stessa per tutti gli spettri e che l'inclinazione del reticolo non sia
cambiata.
Dopo aver calibrato in λ gli spettri e' possibile fare la identificazione delle righe
anche nelle stelle di tipo spettrale avanzato, dove la grande densità di righe rende
difficile una identificazione sicura a colpo d'occhio.
Confrontare i tipi spettrali nominali delle stelle osservate con quelli della libreria
standard inclusi in questi Appunti:
nesci\lezlab3\gray\Gray_contents.html
e verificare che non ci siano errori.
Misura delle larghezze equivalenti delle righe spettrali
Il profilo osservato di una riga spettrale non può essere più stretto del profilo
strumentale dello spettrografo usato. Il parametro dominante e' la larghezza della
fenditura sul piano focale dello spettrografo che nel nostro caso (fenditura da 50
micron) e' di 30 micron; poiché il pixel della DTA e' 24 micron e' ragionevole
aspettarsi una larghezza a metà altezza (FWHM) del profilo strumentale di circa 2
pixel (60 micron). Col reticolo da 600 tr/mm nel nostro spettrografo si hanno 3
A/pixel, quindi una FWHM di 6 A.
Per definizione, la larghezza equivalente di una riga e' l'area compresa tra il
profilo della riga e il livello del continuo sopra di essa, avendo normalizzato a 1 il
continuo stesso.
Occorre quindi fare le seguenti operazioni:
•
•
•
•
determinare il livello del continuo dai due lati della riga in esame
calcolare la retta che passa per questi due punti
dividere il tratto di spettro in esame per questa retta in modo da
normalizzare lo spettro
trovare la gaussiana che meglio riproduce lo spettro osservato: la posizione
del minimo darà la lunghezza d'onda della riga, mentre l'area e' data dal
prodotto della Ampiezza per la Sigma per radice di 2 pi greco.
Vediamo questi passi con Kaleidagraph
Scegliere ad occhio i punti di inizio e fine della riga in esame
selezionare le colonne flusso e lambda nel tratto di spettro che comprende la riga:
assumiamo il flusso in colonna 1 (C1) e le lambda in colonna 0 (C0) ).
scrivere l'equazione di una retta che passa per questi due punti: es.
C2 = [cell(1,1) - cell(37,1)] / [cell(1,0) - cell(37,0)] ∗ [C0 - cell(37,0)] + cell(37,1) ;
cell(r,c) indica il contenuto della casella alla riga r e colonna c
premere run per calcolare: si crea la colonna C2 con i dati della retta.
normalizzare lo spettro al continuo: scrivere l'equazione relativa: C3 = C1/ C2
si crea la colonna C3 con lo spettro normalizzato.
Graficare lo spettro normalizzato (menu' Gallery) e dal menu' Curve-Fit - General
definire la gaussiana di fit:
1.0 - m1 ∗ exp (- 0.5 ∗ [(m0-m2)/m3)²]
;
m1 = 0.5
;
m2 = 4101
;
m3 = 3
in questa formula m0 e' la variabile in ascissa (lambda) mentre m1, m2 ed m3
sono i parametri della Gaussiana (ampiezza, lambda centrale, sigma);
e' necessario fornire a Kaleidagraph i valori iniziali dei parametri, dai quali lui
parte per trovare i migliori per approssimazioni successive.
eseguire il fit: compariranno i valori dei parametri coi loro errori e il valore dello
scarto quadratico medio del fit (NON E' il χ² anche se c'e' scritto così nella
tabella).
Se si prende una riga dell'Idrogeno appare evidente che il fit Gaussiano non e'
adeguato perché le ali sono più estese. Occorrerebbe un profilo somma di una
Gaussiana e una Lorentziana, che si può volendo definire nel menù General
suddetto.
Migliorare la lambda-ascissa
Ora che abbiamo visto come calcolare con maggior esattezza il baricentro delle
righe spettrali si potrebbe voler fare una relazione ascissa-lunghezza d'onda più
accurata (frazione di pixel).
A questo scopo utilizzare le lunghezze d'onda nominali e la posizione del minimo
della riga in pixel e frazioni di pixel. Per il calcolo della posizione del minimo si
può usare un semplice fit gaussiano.
La spettroscopia come mezzo d'indagine
Le righe spettrali, Composizione chimica, Classificazione spettrale,
Misure di velocità , Esempi di fattibilità
Le righe spettrali
Vediamo brevemente come si formano le righe nell'atmosfera di una stella.
I fotoni provenienti dall'interno più caldo vengono assorbiti dagli atomi esterni più freddi alle
lunghezze d'onda corrispondenti ai salti di energia tra i livelli possibili degli elettroni più esterni e
ridiffusi in tutte le direzioni: ne consegue che nella direzione dell'osservatore il flusso di luce a
queste lunghezze d'onda e' attenuato.
Se invece di una stella osserviamo una nube di gas caldo, la luce emessa si concentra su
pochissime lunghezze d'onda, caratteristiche dei livelli energetici degli elettroni più esterni degli
atomi del gas, mentre fuori delle righe l'emissione (il cosidetto "continuo") e' prossimo a zero.
Questa proprietà permise ai primi spettroscopisti di risolvere la annosa questione se tutte le
nebulose fossero fatte in realtà di stelle troppo ravvicinate tra loro per poter essere separate coi
telescopi o fossero invece, come il nome suggerisce, nubi gassose.
Quantitativamente l'intensità di una riga si misura con la cosiddetta larghezza equivalente, che e'
la larghezza che avrebbe una riga, misurata in unità di lunghezza d'onda, se avesse un profilo
rettangolare di area equivalente a quella della riga effettiva.
La riga si dice di assorbimento se lo spettro e' meno intenso all'interno della riga, di emissione se
lo spettro e' più intenso.
Una larghezza equivalente di 1 Angstrom in assorbimento e' una riga stellare molto intensa. Le
righe di emissione delle Quasar possono essere anche centinaia di Angstrom.
Quindi una riga in emissione indica la presenza di gas caldo, mentre una di assorbimento indica
la presenza di un assorbitore più freddo della sorgente posta dietro di essa lungo la linea di vista
dell'osservatore.
Il profilo di una riga spettrale dipende da diversi parametri. Una riga ha comunque una sua
larghezza finita, dovuta al fatto che il tempo di permanenza dell'elettrone sul livello eccitato non e'
zero. Questa larghezza e' però molto piccola rispetto alle altre cause di allargamento nelle
situazioni di interesse astrofisico:
Allargamento per effetto Doppler (termico).
L'agitazione termica del gas nella fotosfera stellare implica una distribuzione maxwelliana
delle velocità degli atomi. I fotoni provenienti dall'interno vengono quindi assorbiti non solo
alla frequenza propria della transizione elettronica, ma anche a frequenze leggermente
superiori e inferiori, con probabilità sempre più piccola quanto più la frequenza e' diversa,
dato che sono sempre meno gli atomi con velocità diversa dal valore medio.
Il profilo risultante e' gaussiano con HWHM = λ (2kT ln(2)/(mc^2))^0.5 dell'ordine di 0.1
Angstrom per T = 10000 K :
in questa formula k e' la costante di Boltzmann, c la velocita' della luce, m la massa
dell'atomo e T la temperatura in Kelvin.
Allargamento per effetto Doppler (turbolento).
Analogo effetto di allargamento gaussiano produce la turbolenza del gas nella fotosfera,
che può essere anche confrontabile con l'allargamento termico.
Allargamento per effetto Doppler (rotazionale).
Se una stella ruota, la proiezione della velocità sulla linea di vista fa si che le diverse zone
del disco stellare emettano a lunghezza d'onda diverse rispetto all'osservatore.
Poiché noi vediamo la stella come un'unica sorgente, il profilo della riga e' la somma dei
contributi delle varie aree della fotosfera stellare: il profilo risultante e' ellittico e la
larghezza della riga fornisce il valore di V sin(i), dove V e' la velocità equatoriale ed i
l'inclinazione dell'asse di rotazione rispetto alla linea di vista.
Allargamento per pressione. I livelli energetici di uno ione sono leggermente alterati dal
campo elettrico generato dalla presenza ravvicinata di altri ioni, tanto più quanto più e'
alta la densità ( e quindi la pressione) delle particelle. Questo fa sì che sia possibile
l'assorbimento di un fotone in un intervallo di lunghezze d'onda più grande. Questo effetto
e' alla base della classificazione spettrale bidimensionale (MK) in quanto le atmosfere delle
stelle giganti sono più rarefatte di quelle delle stelle di sequenza principale e quindi
producono righe più sottili a parità di temperatura (agitazione termica).
Il profilo della riga può essere inoltre modificato dalla presenza, lungo la linea di vista, di altri
strati di materia, circumstellari o interstellari, otticamente spessi o sottili, in quiete o in moto
rispetto alla stella stessa.
Un inviluppo otticamente sottile e in espansione
produce un profilo di riga di assorbimento triangolare sbilanciato verso le lambda corte (caso a),
mentre se e' otticamente spesso il profilo si arrotonda a rami di parabola (caso b).
Una regione di gas in espansione di grandi dimensioni intorno alla stella porta alla formazione di
un profilo diverso da quello delle righe di assorbimento. Se e' otticamente sottile riceviamo luce sia
dal lato in avvicinamento che da quello in allontanamento, con un profilo simmetrico rispetto alla
velocità del baricentro
se la regione non e' otticamente sottile abbiamo sia emissione che assorbimento e il profilo diventa
parabolico.
Se la velocità di espansione e' in accelerazione, si può avere assorbimento dalle regioni esterne ed
emissione da quelle interne; in questo caso si ottiene il profilo P Cygni.
Lo studio del profilo delle righe permette di ricavare informazioni sullo stato della materia stellare
e circumstellare, non ottenibili con altri metodi.
Composizione chimica
Al variare del numero degli atomi assorbitori lungo la linea di vista, la profondità della riga si
modifica come pure il suo profilo.
Se riportiamo in un grafico la larghezza equivalente di una riga di assorbimento in funzione del
numero di atomi, si ottiene la cosiddetta curva di crescita.
La caratteristica saliente e' che l'intensità della riga e' proporzionale al numero di atomi
assorbitori solo per basse abbondanze, poi satura e infine ricomincia a crescere ma solo
proporzionalmente alla radice quadrata del numero di atomi.
Il metodo della curva di crescita e' alla base del calcolo delle abbondanze degli elementi nelle
atmosfere stellari. Molto schematicamente si confronta la curva teorica (calcolata per una certa
specie atomica per una data temperatura e pressione) con la distribuzione dei punti sperimentali,
ottenuta riportando le larghezze equivalenti delle righe di un dato elemento contro le loro
probabilità di transizione: la traslazione di queste curve lungo l'asse orizzontale per portarle a
coincidenza da' l'abbondanza relativa dell'elemento rispetto all'Idrogeno, che e' il principale
costituente (90% in numero di atomi) delle atmosfere stellari.
E' da notare che la parte più sensibile della curva di crescita e' il primo tratto, quello cioè delle
righe con piccola larghezza equivalente.
Le misure di abbondanza richiedono quindi poteri risolutivi molto elevati (R>10000).
Classificazione spettrale
Il primo risultato dello studio spettroscopico delle stelle fu la classificazione morfologica, iniziata
da Secchi e proseguita da Pickering (1900, HD) e perfezionata da Morgan, Keenan e Kellman
(1950, MKK).
Nello schema HD, dovuto principalmente ad Annie Cannon, le classi spettrali sono ordinate per
temperatura superficiale, a partire dalle più calde O per finire alle M, secondo la sequenza
O,B,A,F,G,K,M.
La classificazione viene fatta in base alla presenza di particolari righe di assorbimento e ai loro
rapporti di intensità relativa .
Un esempio della variazione della riga H-γ della serie di Balmer dell'Idrogeno e' dato dalla figura
seguente.
Nella classificazione MK si tiene anche conto della larghezza delle righe, che dipende dalla
pressione del gas e quindi dalla gravità superficiale della stella, distinguendo così le stelle anche
in base al raggio.
Vediamo di seguito alcuni spettri rappresentativi delle varie classi, fatti con un telescopio
amatoriale, un grism Baader da 207 tr/mm e una camera CCD, che coprono l'intervallo da 3800 a
10000 A.
•
•
•
•
•
•
•
O-B
A0-F2
F2-K0
K0-M0
M0-M4
M2-S5
B0e-B8e
Per confronto ecco una analoga serie di spettri fatte con un telescopio Newton da 30 cm, grism
Raibow Optics da 600 tr/mm e macchina fotografica (con pellicola pancromatica).
Notare che in tutti questi spettri la distribuzione dell'energia in funzione della lunghezza d'onda e'
dominata dalla curva di risposta strumentale.
Tipi spettrali principali
O
B
A
F
G
K
M
Misure di velocità
Le misure di velocità radiali sono di grande importanza in astrofisica nei settori più svariati:
•
•
•
misura di velocità radiali di stelle. Queste hanno permesso di evidenziare la rotazione della
nostra Galassia, verificare il moto orbitale della Terra intorno al Sole.
misura della velocità di espansione e contrazione delle stelle variabili (es. Cefeidi) e
conseguente misura delle loro dimensioni.
scoperta di stelle doppie strette dalle variazioni periodiche della loro velocità radiale. Se le
stelle sono di luminosità confrontabile lo spettro osservato e' la somma degli spettri e le
righe spettrali di ciascuna stella variano di lunghezza d'onda al variare della proiezione del
vettore velocità lungo la linea di vista.
Questo permette la misura delle loro masse e dei semiassi delle orbite.
Accoppiato a misure fotometriche, permette anche la misura dei raggi e delle temperature
stellari, permettendo una verifica diretta dei modelli di struttura stellare.
Negli ultimi tempi questa tecnica ha permesso anche la scoperta di numerosi pianeti
extrasolari, che producono variazioni di velocità di poche decine di metri al secondo.
•
Nel campo extragalattico le misure di velocità radiale hanno permesso la scoperta
dell'espansione dell'Universo e la misura della massa degli ammassi di galassie, rivelando
la presenza di materia oscura.
Misure di velocità si possono fare anche su immagini non puntiformi. Se, ad esempio, si fa lo
spettro di Saturno ponendo la fenditura lungo gli anelli, si evidenzia come gli anelli siano costituiti
da tanti corpi indipendenti in moto kepleriano intorno al pianeta e non costituiscono un unico
anello solido.
Se si pone la fenditura lungo l'asse maggiore di una galassia a spirale, si può ottenere il profilo di
velocità di rotazione della galassia intorno al proprio asse. Queste misure permettono di ricavare
la massa della galassia (nota la distanza) e hanno portato, tra l'altro, alla scoperta di materia
oscura nelle regioni esterne.
Qualche esempio numerico
Vediamo ora qualche esempio numerico per vedere quali poteri risolutivi siano necessari per le
applicazioni che abbiamo elencato in precedenza.
•
•
Classificazione spettrale. La classificazione spettrale nel sistema MK (bidimensionale) e'
stata realizzata con lastre fotografiche nel blu con dispersioni di 120 A/mm. Poiché questa
e' la dispersione dell' OMR-10C con il reticolo da 600 tr/mm, appare evidente che questo
tipo di lavoro e' pienamente fattibile.
Misura di velocità radiale. La velocità radiale di una stella si determina tramite l'effetto
Doppler:
v = c (λo - λe) / λe
dove:
v e' la velocità radiale della stella, c la velocita' della luce, λo la lunghezza d'onda osservata
di una riga e λe la lunghezza d'onda emessa.
Una velocità di 30 km/s (la velocità orbitale della Terra intorno al Sole; la velocità relativa
tipica tra due stelle del disco galattico) comporta uno spostamento di 1/10000 della
lunghezza d'onda, ossia 0.5 A per una riga a 5000 A.
Per poter misurare questo spostamento con una decente affidabilità bisogna che
corrisponda a uno spostamento di almeno un pixel sul rivelatore; occorre quindi una scala
di 0.5 A/pixel.
Con la DTA (pixel 24 micron) e l'OMR-10C col reticolo da 600 tr/mm (scala 120 A/mm) un
pixel vale 2.8 A, circa 5 volte meno del necessario. Per questo tipo di misure si dovrebbe ad
esempio usare un reticolo da 1200 tr/mm e avere una camera con pixel da 9 micron.
Lo strumento potrebbe poter rivelare velocità radiali dell'ordine di 150-200 km/s. Queste
velocità sono possibili per stelle dell'alone galattico, o nelle curve di velocità radiale di
binarie strette (tipo W UMa).
Velocità radiali di galassie, che sono dell'ordine di migliaia di km/s sarebbero facilmente
rivelabili, ma le galassie sono troppo deboli per un piccolo telescopio come il TACOR. Si
può forse tentare con i Quasar più brillanti che hanno forti righe di emissione.
•
Misura di larghezze equivalenti (LE). Supponiamo di voler misurare la LE di una riga in
assorbimento da 1 A. Se il profilo fosse rettangolare la sua larghezza sarebbe appunto 1 A,
cioè sensibilmente meno di un pixel. In realtà le righe hanno profili intrinseci
approssimativamente gaussiani (allargamento per turbolenza e agitazione termica) per cui,
se l'intensità dello spettro andasse a zero al centro della riga la larghezza a metà altezza
sarebbe circa 1 A, e al livello del continuo circa 2 A.
Ma il nostro spettrografo (fenditura 50 micron, reticolo 600 tr/mm blazed al primo ordine)
ha un potere risolutivo di 3.6 A, corrispondenti a 1.3 pixel della camera DTA.
In pratica la nostra riga avrà una FWHM di almeno 2 pixel (5.5 A):
la profondità della riga sarà perciò circa (area/FWHM) 1/5.5=0.18: se il continuo vale 1, il
fondo della riga avrà intensità 0.82.
Per poter misurare questa profondità con decente precisione, il livello del continuo deve
essere determinato con un errore dell'1%. Se l'errore fosse puramente Poissoniano (radice
quadrata dei fotoni rivelati) occorrerebbero 10000 fotoni per pixel. In pratica ne servono
molti di più.
•
Vediamo ora se il nostro strumento può rivelare l'allargamento delle righe spettrali per
rotazione nel caso di stelle veloci (150 km/s; stelle di alta sequenza principale, tipi O-A).
Una FWHM strumentale di due pixel (5.5 A) corrisponde a una velocità
v = c (λo- λe) / λe
di 300 km/s a λ =5500 A, quindi anche questa misura e' al limite delle possibilità. Questa
formula ci dice che per rivelare una data velocità conviene cercare di osservare a λ grandi,
quindi verso i 6000-7000 A anziché a 5000. Bisogna anche notare che le righe della serie
di Balmer NON sono adatte a questo studio perché molto allargate per effetto Stark
(allargamento per perturbazione dei livelli energetici da parte degli atomi circostanti).
•
Composizione chimica. Queste misure richiedono misure di righe deboli (LE ~ 0.05 A) con
elevata precisione e quindi sono al fuori della portata del nostro spettrografo.