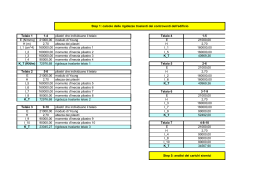
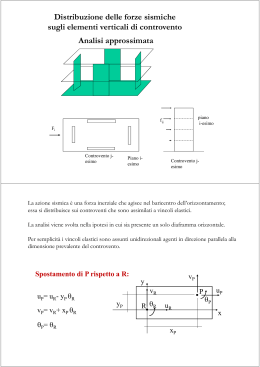
COMPORTAMENTO MECCANICO - DI UN MATERIALE - DI UN ELEMENTO STRUTTURALE - DI UNA STRUTTURA COMPORTAMENTO MECCANICO legame fra • tensioni e dilatazioni • • carichi e deformazioni carichi e spostamenti COMPORTAMENTO MECCANICO • • si può determinare tramite prove si descrive con una legge matematica o con un grafico tensionideformazioni o carico-deformazione o carico-spostamento Fmax = resistenza della struttura max F limite elastico e Fmax limite di rottura r max = resistenza del materiale limite elastico e limite di rottura r COMPORTAMENTO MECCANICO F Fmax comportamento fragile e r comportamento duttile F Fmax e r RIGIDEZZA la capacità di un elemento di opporsi alle deformazioni generate da un carico F k la rigidezza è costante fintanto che l'elemento presenta comportamento lineare Casi particolari rigidezza infinita = deformabilità nulla rigidezza nulla = infinita deformabilità kF F tg per i materiali la rigidezza è chiamata modulo elastico E F fintanto che il comportamento è lineare, la rigidezza è costante oltre il campo elastico, la rigidezza si abbatte si parla di rigidezza, o modulo elastico, secante s Rigidezza e resistenza sono due cose ben diverse e non è detto che vadano di pari passo F Fmax,2 Fmax,1 K1 K2 Lo stesso elemento strutturale ha comportamento diverso a seconda di come è vincolato e del carico che viene applicato. Di conseguenza per lo stesso elemento si definiscono rigidezze e resistenze diverse. RIGIDEZZA ASSIALE Esempio: pilastro soggetto ad un carico centrato tensioni: σ = F/A deformazioni: ε = F/EA F accorciamento del pilastro: h h 0 dh F EA h rigidezza: F F EA k F h h h EA RIGIDEZZA FLESSIONALE F F EJ l3 k 48 F EJ k 3 3 h k 12 EJ h3 La rigidezza ha un ruolo molto importante sulla distribuzione delle forze fra gli elementi strutturali che compongono una struttura. La distribuzione delle forze fra più elementi resistenti, nell'ipotesi di movimento rigido dell'elemento che li collega, avviene proporzionalmente alle rigidezze degli elementi. Se l'elemento di collegamento è rigido, può solo traslare parallelamente a se stesso, perciò gli accorciamenti dei due pilastri sono uguali F k1 E1 A1 h1 k2 E 2 A2 h2 F1 F2 F F1 k1 F2 k 2 F k1 k 2 k1 k 2 F F1 F2 F k1 k 2 k1 F1 F k1 k 2 k2 F2 F k1 k 2 Es: Pilastro in cemento armato soggetto a sforzo normale In assenza di scorrimenti fra acciaio e calcestruzzo, entrambi gli elementi presentano lo stesso accorciamento Aa, Ea Ac, Ec Ec Ac kc h Ea Aa ka h kc Ec Ac Nc N N kc k a Ec Ac Ea Aa Nc N Ec N N c Ac Ec Ac Ea Aa A Ea A Ac nAa c a Ec Distribuzione della forza orizzontale fra le strutture verticali Struttura costituita da un solaio sostenuto da 4 pilastri, che costituiscono 2 telai nella direzione della forza F F Ipotesi di solaio infinitamente rigido nel proprio piano Problema: come si ripartisce la forza fra i due telai Forza centrata R R' F1 F R F2 k1 F1 F k1 k 2 k2 F2 F k1 k 2 F1 Forza eccentrica F e M R FR F2 F*e e F i d i Se l'elemento di collegamento ha una rigidezza finita, la distribuzione non è più semplicemente proporzionale, ma segue comunque le rigidezze. In definitiva gli elementi più rigidi assorbono quote maggiori delle forze e, siccome non è detto che siano anche più resistenti, è probabile che entrino in crisi per primi.
Scaricare