Appunti
Chimica
Casadei Cristiano
Introduzione ........................................................................................................ 6
Struttura della Materia ............................................................................................................................. 6
Teoria atomica e sua evoluzione....................................................................... 7
Teorie Atomiche ...................................................................................................................................... 7
Determinazione dei Pesi Atomici............................................................................................................. 7
Determinazione delle Masse Atomiche Assolute..................................................................................... 7
Esperimento di Thomson ......................................................................................................................... 7
Camera di ionizzazione di Bainbridge ..................................................................................................... 8
Scala dei Pesi Atomici e u.m.a................................................................................................................. 8
Mole e numero di Avogadro .................................................................................................................... 8
Dimensione degli atomi ........................................................................................................................... 9
Struttura degli atomi: l'elettrone............................................................................................................... 9
Proprietà cinematiche dell'elettrone ......................................................................................................... 9
Formule relativistiche di un elettrone....................................................................................................... 9
Determinazione del rapporto e/m........................................................................................................... 10
Rapporto e/m negli atomi....................................................................................................................... 10
Modello atomico di Rutherford ............................................................................................................. 10
Geometria dell'urto di α-nuclei .............................................................................................................. 11
Rivelazione del protone (Rutherford, 1919) .......................................................................................... 11
Rivelazione del neutrone (Curie, 1932) ................................................................................................. 12
Il nucleo dell'atomo .......................................................................................... 13
Protoni e Neutroni.................................................................................................................................. 13
Nuclidi stabili e nuclidi instabili ............................................................................................................ 13
La radioattività....................................................................................................................................... 13
Decadimento radioattivo........................................................................................................................ 13
Decadimento α (A,Z) ⇒ [(A-4),(Z-2)] .............................................................................................. 13
Decadimento β- (A,Z) ⇒ [A, (Z+1)] .................................................................................................. 14
Decadimento β+ (A,Z) ⇒ [A,(Z-1)] ..................................................................................................... 14
Cattura elettronica (cattura K) (A,Z) ⇒ [A,(Z-1)] + raggi X ............................................................... 14
Decadimento γ ....................................................................................................................................... 14
Legge cinetica del decadimento radioattivo........................................................................................... 14
Famiglie radioattive ............................................................................................................................... 15
Famiglie naturali .................................................................................................................................... 15
Famiglia artificiale ................................................................................................................................. 15
Difetto di massa ed energia nucleare ..................................................................................................... 15
Tipi diversi di reazioni nucleari a bassa energia (<100MeV) ................................................................ 16
Schema delle reazioni a bassa energia ................................................................................................... 16
Reazioni prodotte da neutroni................................................................................................................ 16
Fissione nucleare.................................................................................................................................... 16
Modello di fissione basato sul modello a "goccia" ................................................................................ 17
Soglia di fissione.................................................................................................................................... 17
Principi di funzionamento dei reattori nucleari...................................................................................... 17
Le scorie ................................................................................................................................................ 18
La fusione nucleare ................................................................................................................................ 18
Fusione termonucleare ........................................................................................................................... 18
Bilancio energetico ................................................................................................................................ 18
Criterio di Lawson ................................................................................................................................. 19
Processo di nucleosintesi degli elementi nei corpi stellari ..................................................................... 19
La struttura elettronica degli elementi e la loro classificazione periodica.. 20
La nascita della teoria dei quanti............................................................................................................ 20
Effetto Fotoelettrico............................................................................................................................... 21
Leggi dell'effetto fotoelettrico................................................................................................................ 21
Spettri di emissione caratteristici degli atomi ........................................................................................ 22
Spettri caratteristici dell'atomo di idrogeno ........................................................................................... 22
Spettri dei sistemi idrogenoidi ............................................................................................................... 23
2
Principio di combinazione di Rydberg e Ritz .........................................................................................23
I raggi X ed il loro spettro ......................................................................................................................24
Modello di Bohr dell'atomo di idrogeno.................................................................................................24
L'interpretazione degli spettri di raggi X secondo Bohr-Sommerfield ...................................................26
Funzionamento dei L.A.S.E.R. ...............................................................................................................26
Lo spin dell'elettrone ..............................................................................................................................28
Principio di esclusione di Pauli ..............................................................................................................28
Meccanica Ondulatoria .....................................................................................29
Principio di indeterminazione.................................................................................................................29
Onde di de Broglie e la meccanica ondulatoria ......................................................................................30
Equazione di Schrödinger.......................................................................................................................30
L'atomo di idrogeno nella descrizione della meccanica ondulatoria.......................................................31
Orbitali s .................................................................................................................................................32
Orbitali p ................................................................................................................................................32
Orbitali d ................................................................................................................................................33
Le funzioni d'onda degli orbitali atomici ................................................................................................33
Gli atomi con più elettroni nella descrizione della meccanica ondulatoria.............................................33
Principio di Pauli e regola di Hund ........................................................................................................34
La struttura degli atomi nello stato fondamentale...................................................................................34
La classificazione periodica degli elementi ............................................................................................36
Carica nucleare efficace..........................................................................................................................38
Dimensioni Atomiche .............................................................................................................................38
Energia di ionizzazione ..........................................................................................................................38
Affinità elettronica..................................................................................................................................39
Elettronegatività .....................................................................................................................................39
Carattere Metallico .................................................................................................................................39
Previsioni sul tipo di legami ...................................................................................................................39
Altre proprietà ........................................................................................................................................39
Il legame chimico e la formazione delle molecole e dei cristalli...................40
Introduzione............................................................................................................................................40
Concetto generale di legame chimico: l'energia di legame .....................................................................40
Il legame ionico ......................................................................................................................................40
Cloruro di sodio......................................................................................................................................40
Energia reticolare....................................................................................................................................41
Valenza ionica ........................................................................................................................................42
Raggi ionici e geometria dei reticoli cristallini ionici.............................................................................42
Proprietà generali dei composti ionici ....................................................................................................43
Il legame covalente.................................................................................................................................43
Legami σ e π...........................................................................................................................................45
Struttura degli aggregati poliatomici con legami covalenti: molecole, cristalli molecolari, cristalli covalenti
Radicali liberi .........................................................................................................................................46
Legami covalenti polari ..........................................................................................................................46
Legami covalenti polari ed elettronegatività degli atomi........................................................................47
Legame covalente di coordinazione ( legame dativo )............................................................................47
Stati di valenza degli atomi.....................................................................................................................48
Numero di ossidazione ...........................................................................................................................48
Regole per derivare i n.o. .......................................................................................................................48
Stati di ossidazione degli elementi e classificazione periodica...............................................................49
La teoria dei legami di valenza (Heitler-London)...................................................................................49
Risonanza fra due strutture di legame.....................................................................................................50
Orbitali ibridi e geometria molecolare....................................................................................................50
Le funzioni d'onda degli orbitali ibridi ...................................................................................................50
Ibridazione sp3 ........................................................................................................................................51
Ibridazione sp2 ........................................................................................................................................51
Ibridazione sp .........................................................................................................................................51
Ibridazione sp3d2.....................................................................................................................................51
Teoria degli orbitali molecolari ..............................................................................................................51
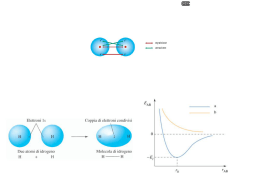
La molecola d'idrogeno nella teoria degli orbitali molecolari ................................................................53
46
3
Confronto tra le due teorie ..................................................................................................................... 53
Molecole biatomiche omonucleari......................................................................................................... 53
Molecole biatomiche eteronucleari........................................................................................................ 54
Strutture tipiche di composti .................................................................................................................. 55
Il legame metallico................................................................................................................................. 56
Reticoli cristallini tipici dei metalli........................................................................................................ 57
La teoria degli orbitali di Bloch ............................................................................................................. 58
Silicio, semiconduttori ........................................................................................................................... 59
Drogaggio .............................................................................................................................................. 59
Legami con interazioni di Van Der Waals ............................................................................................. 60
Legame ad idrogeno............................................................................................................................... 60
I tre stati di aggregazione della materia ......................................................... 61
Introduzione........................................................................................................................................... 61
Lo stato gassoso ..................................................................................................................................... 61
Lo stato solido........................................................................................................................................ 62
Lo stato liquido ...................................................................................................................................... 63
Pressione di vapore di un liquido........................................................................................................... 63
Soluzioni ................................................................................................................................................ 64
Solubilità................................................................................................................................................ 64
Soluzioni ideali ...................................................................................................................................... 65
Soluzioni non ideali ............................................................................................................................... 65
Elettrolisi e processi agli elettrodi.......................................................................................................... 65
Dinamica chimica ............................................................................................. 67
Reazione chimica ed equazione stechiometrica ..................................................................................... 67
Redox..................................................................................................................................................... 67
Redox in forma ionica............................................................................................................................ 67
Rendimento di una reazione................................................................................................................... 67
Peso equivalente .................................................................................................................................... 68
I fondamenti della termodinamica chimica .................................................... 69
Definizioni e concetti generali: i sistemi termodinamici ed il loro stato ................................................ 69
Lavoro in una trasformazione termodinamica........................................................................................ 70
Energia interna di un sistema termodinamico ........................................................................................ 70
Il calore come forma di energia: l’equivalenza tra calore ed energia meccanica ................................... 71
La formulazione del primo principio della termodinamica .................................................................... 71
Entalpia.................................................................................................................................................. 71
Termochimica ................................................................................................... 71
Calore di reazione .................................................................................................................................. 71
Calore standard di reazione.................................................................................................................... 72
Calore standard di formazione ............................................................................................................... 72
Calore standard di combustione............................................................................................................. 72
Calore latente di fusione, di vaporizzazione, di sublimazione ............................................................... 72
Calore di soluzione ................................................................................................................................ 73
Legge di Hess......................................................................................................................................... 73
Equazione di Kirchoff............................................................................................................................ 73
Il secondo principio della termodinamica .............................................................................................. 73
Rendimento della conversione di calore in lavoro: teorema di Carnot .................................................. 74
Il teorema di Clausius e la formulazione del secondo principio della termodinamica: l’entropia.......... 75
Il principio dell’incremento dell’entropia .............................................................................................. 76
Entropia e probabilità termodinamica di stato ....................................................................................... 76
Il terzo principio della termodinamica e l’entropia allo zero assoluto ................................................... 77
Energia libera......................................................................................................................................... 77
Energia libera e lavoro utile................................................................................................................... 77
Applicazioni chimiche dei risultati fondamentali del secondo principio
termodinamica .................................................................................................. 79
4
della
Condizioni termodinamiche di spontaneità di una reazione ...................................................................79
Dipendenza dell’energia libera dalla temperatura e dalla pressione .......................................................80
Reazione chimiche ed equilibrio.............................................................................................................80
Legge dell’equilibrio chimico.................................................................................................................81
Reazioni termodinamiche favorite e non favorite: posizione dell’equilibrio ..........................................81
Espressione della costante di equilibrio per diversi tipi di reazione .......................................................82
Spostamento dell’equilibrio....................................................................................................................83
Equazione di Van’t Hoff.........................................................................................................................84
Equilibri ionici in soluzione....................................................................................................................85
La ionizzazione dell’acqua .....................................................................................................................85
Soluzioni neutre, acide e basiche: pH e pOH .........................................................................................86
Acidi e basi.............................................................................................................................................86
Ionizzazione di un acido o di una base in soluzione acquosa .................................................................87
Acidi e basi monoprotici.........................................................................................................................88
Processi idrolitici....................................................................................................................................88
Soluzione tampone .................................................................................................................................89
Concetto di acido e base secondo Lewis ................................................................................................89
Equilibri di solubilità di composti ionici ................................................................................................90
Equilibri tra fasi diverse .........................................................................................................................90
La regola delle fasi .................................................................................................................................90
Sistemi ad un solo componente ..............................................................................................................91
Diagrammi di stato dei sistemi ad un solo componente..........................................................................92
Termodinamica Elettrochimica ........................................................................93
Considerazioni introduttive ....................................................................................................................93
Generalità sui potenziali elettrodici ........................................................................................................93
Tipi di semielementi galvanici................................................................................................................94
Forza elettromotrice di una cella chimica...............................................................................................94
Potenziale di un semielemento. Serie elettrochimica dei potenziali standard o normali.........................95
Interpretazione dei fenomeni elettrolitici................................................................................................95
Celle chimiche di uso comune e di interesse tecnico. .............................................................................96
Celle di concentrazione ..........................................................................................................................96
Cinetica chimica................................................................................................97
Considerazioni introduttive ....................................................................................................................97
Velocità di reazione................................................................................................................................97
Velocità di reazione e concentrazione delle specie reagenti: equazioni cinetiche ..................................97
Determinazione sperimentale dell'equazione cinetica.............................................................................98
Meccanismi di reazione. Il complesso attivato .......................................................................................98
Meccanismi di reazione ed equazioni cinetiche......................................................................................99
L'equilibrio chimico dal punto di vista cinetico......................................................................................99
Velocità di reazione e temperatura: teoria delle collisioni molecolari per le reazioni tra gas...............100
Catalisi .............................................................................................................102
Generalità .............................................................................................................................................102
Catalisi omogenea.................................................................................................................................102
Catalisi eterogenea................................................................................................................................102
5
Introduzione
Struttura della Materia
Consideriamo un sistema chimico come quello in riportato in figura. Le quattro componenti sono separate da superfici precise: si tratta di un sistema polifasico. Misurando la
densità in ogni punto, otterrò valori caratteristici per i diversi componenti. Ogni porzione
è omogenea dal punto di vista fisico e costituisce una fase diversa. Una fase è una parte
del sistema chimico fisicamente omogenea: anche se il concetto qui espresso di fase è impreciso, è in ogni caso valido perché non si riuscirà mai a misurare grandezze come i pesi
atomici o i volumi atomici. Si ha una fase sola se i componenti si mescolano fino ad un
livello molecolare (come gas oppure l'acqua con l'alcool etilico). Una specie chimica può
essere uno degli elementi della tavola periodica o uno dei loro composti. I composti obbediscono a leggi fisse e costanti. Consideriamo l'ossido di mercurio HgO: è di colore rosso.
Se è portato a 400° C, si scinde in Hg e O. Allora un composto è tale se si può scindere
nelle sue componenti tramite i metodi ordinari della chimica: mediante innalzamento della
temperatura (fino a 1000°-2000°C), attraverso irraggiamento da radiazioni (purché non
nucleari) o tramite elettricità (non troppo forte).
6
Teoria atomica e sua evoluzione
Teorie Atomiche
L'ipotesi atomica fece il suo ingresso nella scienza dopo la scoperta delle leggi fondamentali ponderali che regolano le combinazioni chimiche.
1) Legge della conservazione di massa (Lavoisier): la massa totale dei reagenti è uguale a quella dei prodotti in ogni reazione
chimica. Dopo Einstein si esprime affermando che la somma di massa ed energia si conserva.
2) Legge delle proporzioni definite (Proust): in ogni composto i singoli componenti sono presenti in quantità ben definite. Per
esempio, dato 1 gr. di H2, ho bisogno di 8 gr. di O per formare H2O. Ci sono tuttavia delle eccezioni dette reazioni non stechiometriche, come l'ossido di silicio, che invece di essere SiO, spesso lo si trova nella forma SiO.
3) Legge delle proporzioni multiple (Dalton): se due elementi combinandosi possono dare dei composti diversi, tenendo fissa
la quantità di uno dei due reagenti, allora la quantità dell'altro varia da composto a composto. Vale a dire che quando due
elementi possono combinarsi insieme in rapporti ponderali diversi, per dare composti diversi, le quantità di uno di loro che
nei vari casi si combinano con la medesima quantità dell'altro, stanno fra loro in rapporti espressi da numeri interi generalmente piccoli. Ad esempio l'azoto (N) e l'ossigeno (O) si possono combinare in:
( 1 gr. N + (0,57x1) gr. O )
N2O
( 1 gr. N + (0,57x2) gr. O )
NO2
N2O3 ( 1 gr. N + (0,57x3) gr. O ).
Si usano atomi interi, non divisibili. La teoria di Dalton muove dal postulato che la materia sia formata da particelle discrete,
chiamate atomi perché non ulteriormente divisibili.
Determinazione dei Pesi Atomici
Abbiamo visto che nella teoria atomica di Dalton, il principale attributo che caratterizza le varie specie d'atomi è la loro massa.
Per ragioni di comodità pratica, si preferì utilizzare, piuttosto che i valori assoluti, estremamente piccoli, i valori relativi definiti
dal rapporto tra le masse atomiche e la massa di un elemento preso convenzionalmente come campione di riferimento. Tali valori relativi vennero chiamati pesi atomici. Il criterio per la determinazione univoca dei pesi atomici si deve agli studi di Avogadro e Cannizzaro. Interpretando un'osservazione di Gay-Lussac, si formulò la nota Legge di Avogadro: volumi uguali di gas
diversi, nelle stesse condizioni di temperatura e di pressione, contengono lo stesso numero di particelle. Alla base dell'opera di
Avogadro sta il nuovo concetto di molecola, cioè un raggruppamento di atomi fra loro stabilmente legati. Per la determinazione
del peso atomico, Avogadro indicò la proporzione:
g
M
g
=
⇒ M = Mr * = Mr * p
gr Mr
gr
Cannizzaro, invece, indicò il seguente metodo: per determinare il peso atomico di un elemento basta considerare un gran numero di suoi composti, determinare di ciascuno il peso molecolare e dedurre la quantità dell'elemento considerato contenuta in una
quantità di esso uguale al suo peso molecolare: il peso atomico dell'elemento è così definito dal valore più basso che si trova.
Determinazione delle Masse Atomiche Assolute
La determinazione dei valori delle masse atomiche assolute è stata resa possibile dalle tecniche della spettrometria di massa il
cui padre fu Thomson. Con l'esperienza di Thomson venne a cadere la convinzione che ogni elemento fosse composto di atomi
tutti uguali: le diverse specie di atomi di uno stesso elemento vennero dette isotopi.
Esperimento di Thomson
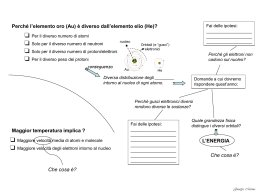
L'esperimento di Thomson prevede l'uso di un tubo contenente gas
neon in condizioni di vuoto spinto. Sotto l'azione di sonde elettriche
prodotte da un'alta differenza di potenziale, (applicata a due elettrodi metallici), viene provocata la ionizzazione di un gran numero
di atomi del gas, in modo da generare uno sciame di ioni positivi ed
elettroni. Gli ioni positivi sono attratti dal catodo (negativo) ed accelerati dal campo elettrico. Il catodo si presenta come una superficie che presenta un piccolo foro, dal quale gli ioni passano per inerzia. Gli ioni che passano, subiscono poi l'influsso di un campo elettrico ed uno magnetico tra loro paralleli e perpendicolari alla
direzione di propagazione dello sciame di particelle. Sotto l'azione contemporanea dei due campi, gli ioni vengono deviati dal
loro cammino a seconda della velocità, carica e massa che possiedono. Alla fine si trova che le particelle caratterizzate da uno
7
stesso valore M/q, ma aventi velocità diverse, si distribuiscono lungo un ramo di parabola, il cui asse è parallelo alle linee di
forza dei due campi. Gli atomi di neon ionizzati, sotto l'azione combinata dei due campi, si distribuiscono in rami di parabole
che possono essere tracciate solamente da particelle di massa diversa, cioè i diversi rami di parabola corrispondo a diversi valori del rapporto M/q. Tuttavia il metodo di Thomson non è di elevata sensibilità e la precisione della misura non è molto alta.
Camera di ionizzazione di Bainbridge
Gli atomi di un determinato elemento vengono trasformati in ioni sotto il bombardamento di un fascio di elettroni ad alta energia, emessi per effetto
termoionico da un filamento metallico incandescente. Gli ioni positivi, accelerati da una d.d.p., entrano attraverso una sottile fenditura dentro un selettore di
velocità, dove sono sottoposti all'azione contemporanea di un campo elettrico
( definito come Fe = q * E ) e di un campo magnetico ( Fb = q * B * v ). A
questo punto, passano attraverso la fenditura seguente solo gli ioni con velocità tale da rendere uguali e contrarie ( e quindi inefficaci ) le forze Fe ed Fb.
E
Fb = Fe ⇒ q * B * v = q * E ⇒ v =
B
Quindi gli ioni con velocità v=E/B passano attraverso l'ultima fenditura, mentre gli altri (deviati perché le forze non si elidono
nel loro caso), andranno ad infrangersi contro la parete. Nell'ultima camera, gli ioni sono sottoposti ad un campo magnetico B'
costante ed uniforme, in modo tale che essi seguiranno una traiettoria circolare (a causa della forza di Lorentz). Tale traiettoria
varierà di raggio a seconda del valore M/q dello ione. Infatti, applicando il 2° principio della dinamica e considerando che
l'accelerazione centripeta è data da ac=v2/r, trovo che, equivalendo la forza di Lorentz con la forza centripeta:
Fb′ = q * v * B ′ = M *
v2
M v
M
E
*
*
⇒r=
=
r
q B′ q B * B′
(Ho ricordato che v =
E
)
B
Quindi gli ioni deviati dal campo B' vengono raccolti sulla superficie fluorescente a distanza diversa dalla fenditura a seconda
del rapporto M/q, e quindi dal valore di M (visto che q è uguale alla carica elettrica elementare).
Tutta l'apparecchiatura è mantenuta sotto vuoto spinto.
Scala dei Pesi Atomici e u.m.a.
Visto l'ordine di grandezza, non è comodo utilizzare i valori assoluti delle masse atomiche, ma è più comodo fare riferimento a
dei valori relativi ad unità di misura convenzionale, chiamata unità di massa atomica o u.m.a. Tale concetto ha portato alla definizione dei pesi atomici degli elementi. All'inizio venne preso come riferimento l'idrogeno, il più leggero degli elementi, e si
pose il suo peso atomico pari ad 1. Poi, constatando che l'ossigeno era presente più spesso nei componenti chimici, si prese
quest’ultimo come riferimento e si pose il suo peso atomico pari a 16. Questa scelta entrò in crisi con la scoperta degli isotopi
dell'ossigeno. Allora si propose di porre uguale a 16 il peso atomico della specie più leggera degli isotopi di ossigeno. Infine,
per risolvere il dualismo delle scale che ne risultò, venne definita come unità di peso atomico la dodicesima parte dell'isotopo
più leggero del carbonio.
Da cui 1 u.m.a. = 1,66*10-24 gr.
Mole e numero di Avogadro
Si definisce grammo-atomo la quantità di un elemento, espressa in grammi, uguale al suo peso atomico e si definisce grammomolecola la quantità di una specie chimica, semplice o composta, espressa in grammi, uguale al suo peso molecolare (si noti
che per le specie chimiche che non hanno struttura molecolare, come i composti ionici o i cristalli a struttura covalente, si utilizza il peso-formula che ne specifica la composizione, e la grammo-formula, cioè la quantità in grammi uguale al peso formula). Allora il medesimo numero di atomi è contenuto in un grammo-atomo di un qualunque elemento ed il medesimo numero di
molecole è contenuto in una grammo-molecola di una qualunque specie chimica. Tale numero è detto numero di Avogadro ed
il suo valore è pari all'inverso dell'unità di massa atomica:
N=
1
1
=
= 6,023 * 10 23
u . m . a . 1,66 * 10 −24
Un numero di particelle unitarie di una data specie uguale al numero di Avogadro viene chiamato mole. La mole è l'unità di riferimento per esprimere la quantità di una specie materiale qualsiasi. Riassumendo otteniamo:
• Peso atomico = Peso dell'atomo / Peso unità pesi atomici
• Peso molecolare = Peso molecola / u.p.a.
8
(u.p.a. =
1
C)
12
Dimensione degli atomi
Consideriamo un elemento metallico di massa atomica media, ad esempio il ferro, il cui peso atomico è 55,847 u.p.a. Conoscendo la sua densità (7,86 gr./cm3) possiamo determinare il volume di un grammo-atomo (V=7,1 cm3). Tale volume contiene
un numero di atomi pari al numero di Avogadro, per cui il volume di un atomo lo si ottiene dividendo il volume di un grammoatomo per il numero di Avogadro (Va=11,5 *10-24 cm3).
Considerando l'atomo come una sfera, il suo raggio è quindi dell'ordine di 10-8 cm, cioè di un Amstrong (Å).
Struttura degli atomi: l'elettrone
Abbiamo visto che, in quanto a proprietà chimiche, l'atomo è la più piccola unità che le mantiene inalterate. Tuttavia esistono
anche particelle subatomiche. La scoperta che gli atomi non sono particelle elementari, ma sistemi composti, venne fatta da Hittorf che, studiando il passaggio dell'elettricità attraverso gas rarefatti sotto elevate differenze di potenziale, scoprì i raggi catodici, costituiti da particelle materiali portatrici di una carica elettrica negativa ed estremamente piccole, molto più piccole di un
atomo. Tali particelle vennero nominate elettroni. L'elettrone è definito in base alle sue proprietà fisiche: carica (e) e massa (m). La carica di un elettrone è universale ed immodificabile. Dunque qualsiasi
altra carica è un suo multiplo. Ma quanto vale tale carica ? Tra i due elettrodi, nel sistema in figura, c'è
una d.d.p. V. Avviene una dissociazione elettrolitica per cui:
AgNO3 ⇒ Ag+ + NO3L'argento si è visto strappare via un elettrone (ed è diventato uno ione positivo). Ora Ag+ migra sull'elettrodo negativo, dove si deposita formando un patina d'argento. Calcolando la quantità di energia da
far passare tra gli elettrodi per far depositare una mole di un qualsiasi ione monovalente, si è visto che
tale quantità è costante e vale 96500 Coulomb. Considerato che in una mole di ioni ci sono Na ioni ognuno dei quali ha perso
un elettrone, ottengo la carica dell'elettrone dividendo l'energia spesa per il numero di Avogadro:
|e|=
96500
= 1,6*10-19 Coulomb
Na
• Effetto termoionico: un filamento, portato ad alta temperatura tramite un passaggio di corrente, emette degli elettroni.
• Effetto fotoelettrico: espulsione di elettroni dalla superficie di un corpo tramite un bombardamento di radiazioni elettromagnetiche.
• Scarica nei gas: facendo il vuoto in un cilindro, si riescono a provocare scariche elettriche e quando la pressione diviene
dell'ordine di 10-4 Torr, dal catodo (polo negativo) partono raggi catodici, composti da elettroni.
Proprietà cinematiche dell'elettrone
L'apparecchiatura è mantenuta in uno stato di vuoto spinto. Volendo studiare la traiettoria dell'elettrone emesso dal filamento, se non ci fosse il vuoto l'elettrone urterebbe contro le molecole dell'aria, e sullo schermo non riuscirebbe ad apparire niente. Per comodità, consideriamo solo gli elettroni che si propagano parallelamente lungo l'asse del tubo cilindrico. Dopo che il fascio è passato per il collimatore, se non è disturbato, arriva
a colpire lo schermo fluorescente, illuminando un punto (spot) indicato con O. Dunque,
se l'elettrone non è soggetto a campi di forza, si propaga rettilinearmente. Per interrompere il fascio elettronico possiamo porre davanti ad esso un mulinello e vedremo che esso si muoverà. Ciò ci dice che l'elettrone
possiede quantità di moto. Inoltre se poniamo il fascio in vicinanza di un campo elettrico o magnetico vedremo che esso verrà
deflesso. Riassumendo possiamo dire che l'elettrone possiede le seguenti proprietà meccaniche:
• Propagazione rettilinea
• Quantità di moto
• Deflessione in campo elettrico/magnetico
L'energia cinetica dell'elettrone, infine, vale:
Ec= ½ * mv2 = eV
L'unità di misura usata è l'elettronvolt che rappresenta l'energia cinetica acquisita da un elettrone accelerato da una d.d.p. di 1
Volt.
Formule relativistiche di un elettrone
La massa di un elettrone non è costante. Chiamiamo m0 la massa a riposo e mv la massa alla velocità v, allora abbiamo:
m0
mv =
v2
1− 2
c
9
Questo ci dice che la massa dell'elettrone dipende dalla sua velocità:
mv = m 0 +
Ec
c2
Da Einstein ho che l'energia intrinseca dell'elettrone vale:
E0 = m0 * c2 = 0,51MeV
2
Etot = E0 + Ec = m 0 * c = c * p2 + m 2 c 2
1−
v2
c2
dove p è la quantità di moto dell'elettrone e c la velocità della luce. Cerchiamo ora la massa dell'elettrone. Per ottenerla
determiniamo il rapporto e/m.
Determinazione del rapporto e/m
Indichiamo con B l'intensità del campo magnetico e con E quella del campo elettrico e con Fb ed Fe le rispettive forze esercitate dai due campi
sulle particelle che finiscono nel loro raggio d'azione. Le forze esercitate
sull'elettrone sono Fe=e * E ed Fb=e * B * v (forza di Lorentz)
Campo elettrico, campo magnetico e direzione di propagazione dell'elettrone formano una terna di assi ortogonali nello spazio. Se un elettrone
giunge in O, significa che non ci sono interferenze, oppure che campo
magnetico e campo elettrico si equilibrano:
Fe=Fb ⇒ e * E = e * B * v ⇒ v =
E
B
Ricordando che l'energia cinetica è ½ mv2, posso ricavare il rapporto e/m che cercavo:
½ m * v2 = eV ⇒ (ricordo che v=
E2
E
) ⇒ ½ m * 2 = eV
B
B
e
E2
=
m 2 * B2 * V
Sperimentalmente si trova quindi che m = 9*10-28 = 10-27 gr. Infine, un'ultima proprietà dell'elettrone è che esso si comporta
come una trottola (spin), cioè ha una proprietà di rotazione su se stesso.
Rapporto e/m negli atomi
Mendelev voleva, come vedremo, classificare gli elementi noti con il seguente criterio:
• orizzontalmente secondo il peso atomico crescente
• verticalmente secondo proprietà chimiche affini
C'erano però tre coppie d'eccezione che fra l'altro comprendevano potassio, cobalto e nichel. Ritornando ora alla struttura degli
atomi, la scoperta dell'elettrone portò Thomson a formulare il primo modello della struttura dell'atomo (modello a panettone)
concependolo come una sfera omogeneamente caricata positivamente in cui sono immersigli elettroni dotati di carica negativa.
Le posizioni che gli elettroni occupano all'interno dell'atomo sono determinate dall'equilibrio tra le forze di attrazione verso il
baricentro delle cariche positive e le forze intermolecolari di repulsione. La particella positiva avente una carica in valore assoluto uguale a quella dell'elettrone è chiamata protone (la cui massa è 1822 volte maggiore di quella dell'elettrone). Tale ultimo
fatto indicò però che il corpo positivo degli atomi non potesse essere composto di soli protoni.
Modello atomico di Rutherford
L'analisi delle radiazioni emesse da elementi radioattivi, mostrarono
che esse sono costituite da tre diverse componenti:
1. le radiazioni α, di natura corpuscolare e formate da particelle
positive con cariche pari a 2e e massa quattro volte superiore
all'idrogeno;
2. radiazioni β, di natura corpuscolare, formate da elettroni;
3. radiazioni γ, di natura elettromagnetica.
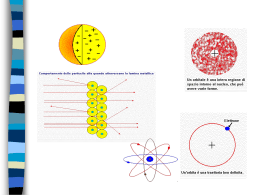
Nel suo esperimento Rutherford indirizzò dei fasci di particelle α,
emesse ad altissima velocità da sostanze radioattive, contro dei fogli
metallici molto sottili e vide che, mentre la maggior parte delle particelle non veniva deviata dalla traiettoria, una piccola parte
10
subiva delle considerevoli deviazioni, ed alcune erano respinte all'indietro con deviazioni angolari che raggiungevano i 180°.
Tali risultati non potevano essere interpretati in base al modello atomico di Thomson: per spiegare questo si doveva ammettere
che la carica positiva e la massa dell'atomo fossero concentrate in un nucleo centrale molto piccolo rispetto all'intero volume
dell'atomo e che lo spazio intorno fosse sostanzialmente vuoto e occupato dagli elettroni, in grado di neutralizzare la carica positiva del nucleo. Nacque così il modello nucleare dell'atomo, in cui gli elettroni venivano concepiti in continua rotazione attorno al nucleo positivo (modello planetario).
Geometria dell'urto di α-nuclei
Consideriamo la legge di Coulomb:
F = k*
q1 * q 2 2 * e * e n
=
r2
r2
Se tuttavia l'elettrone passa ad una distanza minore di Rn (raggio del nucleo) , avremo un urto. Calcoliamo l'angolo minimo di validità della legge
di Coulomb:
Nα(θ)=f(θ)
La funzione Nα(θ) sperimentalmente è circa uguale a f(θ) teorica, purché
sia en=2e.
Sec(θ0)=
M * v2
* Rn − 1
e * en
⇒ da cui ottengo ⇒
2 * z * e2 1
= mv 2
rmin
2
Con questa formula si ottiene una stima del raggio nucleare, che è di 10-12 cm. Tutta la massa atomica è concentrata nel nucleo.
Lo studio quantitativo delle particelle α e della loro distribuzione angolare, portò Rutherford a calcolare la carica positiva dei
nuclei, che risultò essere pari al numero atomico dell'elemento considerato. La carica nucleare risulta così circa 0,5-0,4 volte il
peso atomico. Da tale considerazione si intuì che il nucleo non poteva essere formato di soli protoni. Fu Chadwick che scoprì il
neutrone, una particella che non porta alcuna carica elettrica e che ha una massa circa uguale a quella del protone. Ma, se nel
nucleo è concentrata solo la carica positiva, come riesce a stare assieme ? Consideriamo l'atomo di idrogeno: esso è costituito
da un protone ed un neutrone (r = 0,5 Å). La forza di Coulomb è dell'ordine di 10-8 N. Due protoni si respingono con una forza
100000 volte più forte di quanto si attraggano un elettrone ed un protone. Allora è logico pensare che intervenga una forza a
tenere insieme il nucleo. Questa forza la chiamo forza nucleare forte.
Le 4 forze in natura sono:
I.
ELETTROMAGNETICA
1
II.
NUCLEARE FORTE
100
III.
NUCLEARE DEBOLE
10-11
IV.
GRAVITA'
10-36
( I valori sono ottenuti in rapporto all'interazione elettromagnetica, posta a 1 )
Si spiega allora come la nucleare forte (100) possa tenere assieme i nuclei a dispetto della forza repulsiva.
Rivelazione del protone (Rutherford, 1919)
La reazione che avviene dentro la camera è:
N+α⇒O+p
11
Rivelazione del neutrone (Curie, 1932)
Dalla sorgente partiva una particella α che andava a colpire la lastra di berillio. Da questa partiva una particella,
provocata dalla reazione Be94+α42 ⇒ C126 + n10. Questa
era una particella allora sconosciuta che riusciva a passare
una lastra di piombo spessa 1,5cm, che all'epoca era ritenuta impermeabile a qualunque particella nota (protoni,
elettroni, α, γ). Curie si accorse che "qualcosa" riusciva a
passare la lastra di piombo, in quanto l'elettroscopio posto
a contatto con una camera di ionizzazione, contenente gas
azoto ed ossigeno, rilevava la presenza di un campo elettrico. Questo campo elettrico era dovuto al passaggio attraverso i gas di una particella ad alta velocità che, urtando contro gli atomi di azoto o di ossigeno, riusciva a
strappare loro l'elettrone esterno e quindi ionizzandoli.
Dopo la sua rivelazione, il neutrone fu studiato più approfonditamente e si notò che questa particella è contenuta
all'interno del nucleo degli atomi insieme ai protoni. Inoltre si notò che i neutroni sono particelle elettricamente neutre e con
massa di poco superiore a quella del protone. Sono di notevole importanza le reazioni atomiche che avvengono tramite i neutroni, soprattutto la fissione nucleare che viene utilizzata per produrre armi potentissime o anche per la produzione di energia
tramite apposite centrali elettriche.
Si noti inoltre che, essendo il neutrone una particella di massa considerevole, quando viene accelerato (neutrone veloce) acquista una energia cinetica tale da conferirgli un alto potere penetrante. Ulteriori informazioni verranno date nel capitolo successivo.
12
Il nucleo dell'atomo
Protoni e Neutroni
Abbiamo visto che gli atomi sono formati da un nucleo, in cui sono presenti protoni e neutroni, intorno al quale si muovono gli
elettroni. Protoni e neutroni, essendo le particelle costitutive dei nuclei, vengono detti nucleoni. Il protone ha una massa di
1,00728 u.m.a. ( = 1,67 * 10-24 gr.) ed una carica positiva di circa 4,8*10-10 unità assolute elettrostatiche. Il neutrone ha una
massa di 1,00867 u.m.a. ( = 1,68 * 10-24 gr.) ed è elettricamente neutro.
• Numero di massa (A) = numero complessivo dei nucleoni di un atomo.
• Numero atomico (Z) = numero di protoni di un atomo.
Se Z è costante ed A varia, ogni variante di A rappresenta un isotopo dell'elemento.
Nuclidi stabili e nuclidi instabili
Si chiamano nuclidi le diverse specie di atomi caratterizzate da nuclei di definita
composizione: i nuclidi si dividono in stabili ed instabili. La stabilità dei nuclidi dipende dal rapporto tra il numero dei neutroni ed il numero dei protoni.
Rappresentiamo un diagramma in cui i punti rappresentano i nuclidi conosciuti.
Dalla figura vediamo che fino a Z=20 la striscia coincide con la retta R=A-Z e poi,
col crescere di Z, tende a prevalere sempre più il numero dei neutroni su quello dei
protoni. I nuclidi i cui punti rappresentativi cadono al di fuori della fascia di stabilità, indicata dalla retta, sono instabili e tendono a trasformarsi spontaneamente in
modo da alterare il rapporto tra neutroni e protoni fino a farlo rientrare nella fascia
di stabilità. La manifestazione delle trasformazioni spontanee, dei nuclidi instabili,
viene detta radioattività. Si noti che, fra i nuclidi stabili, i più numerosi sono quelli
con numero pari di neutroni e numero pari di protoni, mentre quelli meno numerosi
sono quelli con numero dispari di neutroni e numero dispari di protoni.
La radioattività
Si tratta di un fenomeno tipicamente nucleare individuato per caso nel 1866 da Becquerel. Coi materiali radioattivi cadeva uno
dei principali presupposti della chimica, ossia che gli atomi non si trasformassero né si dividessero. Addirittura la radioattività
fu scoperta ancora prima che Rutherford intuisse la presenza di un nucleo nell'atomo. Il fenomeno radioattivo non dipende dai
legami chimici, quindi non serve sapere se l'elemento radioattivo si presenta solo o è combinato con altri elementi. Le energie
in gioco nei processi radioattivi sono milioni di volte più alte delle normali reazioni ( si arriva fino a 100 MeV). I fenomeni radioattivi sono indipendenti dalle condizioni di temperatura, campi elettrici e magnetici (a meno che non ci siano enormi variazioni degli stessi). Si parla di decadimento radioattivo perché i nuclidi instabili decadono emettendo radiazioni diverse e, perdendo la loro identità primitiva, si trasformano in altre specie più vicine alla fascia di stabilità.
Decadimento radioattivo
Le radiazioni che i nuclei emettono durante il decadimento sono di quattro tipi:
I.
Radiazione α: particella definita come He42 dotata di un'elevata energia (dell'ordine dei MeV);
II. Radiazione β-: emissione di elettroni (carichi negativamente);
III. Radiazione β+: emissione di positroni (elettroni a carica positiva);
IV. Radiazione γ: onde elettromagnetiche di piccola lunghezza d'onda (l < 0,1A°), dotate quindi di alta energia e di un forte
potere penetrante. Solitamente accompagnano le altre emissioni.
Un altro esempio di radioattività nucleare è la cattura elettronica che si verifica quando il nucleo cattura l'elettrone dell'orbita
più interna. Produce anche emissione di raggi X. Studiamo ora più in dettaglio i vari tipi di decadimento.
Decadimento α
(A,Z) ⇒ [(A-4),(Z-2)]
Il decadimento α è caratteristico dei radionuclidi pesanti (Z>82, A>20). Con l'emissione di una particella α, il nuclide originario si trasforma in un isotopo dell'elemento che lo precede di due posti nella tavola periodica:
X(A,Z) ⇒ Y(A-4,Z-2) + α42
Le particelle α vengono emesse dai nuclei con elevata energia cinetica, tuttavia hanno uno scarso potere penetrante.
13
Decadimento β-
(A,Z) ⇒ [A, (Z+1)]
Tale tipo di decadimento è caratteristico dei nuclidi con un rapporto fra neutroni e protoni eccessivamente alto. Come fa un elettrone ad essere nel nucleo ? È necessario ammettere, come fece per primo Fermi nel 1934, che nel nucleo si possa avere una
reazione del tipo:
n10 ⇒p11 + β-0-1 + n
dove n è il neutrino, una particella che non interagisce né con la forza elettromagnetica né con la forza nucleare forte. Essa non
ha carica né massa, però è responsabile della interazione nucleare debole. Ha un forte potere penetrante. Nel decadimento βrimane invariato il numero di massa, mentre aumenta di un'unità il numero atomico:
X(A,Z) ⇒ Y[A,(Z+1)] + β-0-1
Le particelle β- hanno una massa 7000 volte minore delle particelle α ed hanno una velocità di gran lunga maggiore, per cui
hanno un maggior potere penetrante.
Decadimento β+(A,Z) ⇒ [A,(Z-1)]
Il decadimento β+ è caratteristico dei nuclidi con un rapporto troppo basso tra neutroni e protoni. La trasformazione di un protone in un neutrone, con l'espulsione di un elettrone positivo (positrone) e di un neutrino avviene in questo modo:
p11 ⇒ n10 + β+01 + n
A seguito di questo decadimento (di origine artificiale), il nuclide originario si trasforma in un elemento che lo precede di un
posto nella classificazione periodica:
X(A,Z) ⇒ Y[A,(Z-1)] + β+01
Cattura elettronica (cattura K)
(A,Z) ⇒ [A,(Z-1)] + raggi X
Il rapporto tra neutroni e protoni può essere aumentato anche con la cattura da parte del nucleo di un elettrone extranucleare
che gli ruoti intorno a piccola distanza (come nel caso dell'orbita K, cioè quella più interna). L'elettrone catturato interagisce
con un protone trasformandolo in un neutrone:
X(A,Z) + e0-1 ⇒ Y[A,(Z-1)]
Il decadimento per cattura elettronica è frequente nei radionuclidi con numero atomico Z elevato e si manifesta esternamente
tramite l'emissione spontanea di raggi X.
Decadimento γ
La radiazione γ è di natura elettromagnetica, simile ai raggi X, alla luce o alle onde radio. Di
solito accompagna uno degli altri decadimenti. Perché ? Come si vede nel disegno, l'energia
del nucleo non può essere un valore qualsiasi. Esso è un valore quantizzato in livelli ben definiti. Tra un livello e l'altro vi è uno spazio "proibito". Se in seguito ad un decadimento
α, β+ o β- un nucleo si trova in questa regione interdetta, esso precipita al livello E0 e per far
questo libera l'energia in più (∆E) tramite l'emissione di un'onda elettromagnetica. La lunghezza d'onda di questa onda dipenderà dal valore del ∆E (di solito sufficientemente alto).
Legge cinetica del decadimento radioattivo
Il decadimento spontaneo di un radionuclide è caratterizzato dalla seguente proprietà: il numero degli atti elementari di disintegrazione che si compiono nell'unità di tempo è sempre proporzionale al numero di radionuclidi presenti nell'istante considerato.
La legge che regola la loro disintegrazione è il caso e l'unica cosa che è rigorosamente determinata è la probabilità che ogni atomo ha di disintegrarsi in un determinato intervallo di tempo:
dp = Kd * dt
dove dp è la probabilità che in un istante dt si disintegri un atomo radioattivo, mentre Kd è la costante di decadimento. Se si
moltiplica tale costante per il numero degli atomi presenti, si ottiene il numero di atomi che si disintegrano nell'unità di tempo.
Sia nt il numero degli atomi originari esistenti al tempo t e dn la variazione di tale numero nell'intervallo di tempo dt successivo:
−
dn
dn
= K d * nt ⇒ ∫ −
= K d * dt ⇒ n t = n 0 * e − K d *t
dt
dt ∫
Tale legge rappresenta la legge cinematica del decadimento radioattivo che ne regola la velocità. Secondo tale legge, il numero
degli atomi radioattivi decresce esponenzialmente nel tempo, quindi il decadimento totale di una certa quantità di sostanze radioattive richiederebbe teoricamente un tempo infinito. Per questo motivo, per definire la vita probabile di un determinato tipo
14
di nuclide radioattivo, ci si riferisce al tempo di dimezzamento che rappresenta il tempo necessario affinché il numero di atomi
originario si riduca della metà.


t
n0
 n0 


1
1
n
0
t=
⇒ t½=
* ln  ⇒ per t½ = si ha nt=
* ln
2
2
n 
Kd
Kd
 nt 
 0
 2 
1
ln
2
t½=
* ln 2 =
Kd
Kd
Il semiperiodo è una costante caratteristica di ogni particolare specie di radionuclide e ne rappresenta la vita probabile. La vita
media dei radionuclidi è invece data da q=1/Kd ed è quindi maggiore della vita probabile.
Famiglie radioattive
Tutti i nuclidi derivanti da uno stesso capostipite attraverso una catena di decadimenti successivi, rappresenta una famiglia radioattiva ed essi stanno tra loro in veri e propri rapporti di filiazione che è possibile rappresentare tramite un'espressione generale del tipo 4n+n'
Famiglie naturali
• U238⇒ 4n+2 ⇒ Pb206
• U235⇒ 4n+3 ⇒ Pb207
• Th232⇒ 4n ⇒ Pb208
Famiglia artificiale
• Np237⇒ 4n+1 ⇒ Bi209
Difetto di massa ed energia nucleare
La massa di un qualsiasi nucleo (misurabile con precisione dalle tecniche della spettrometria di massa) risulta inferiore alla
somma delle masse dei nucleoni componenti. La differenza Dm tra la somma delle masse dei nucleoni componenti ed il valore
effettivo della massa nucleare, determinato sperimentalmente, è detta difetto di massa.
∆m= Z * mp + (A-Z) * mn - mnucl
Il difetto di massa è la misura dell'energia nucleare, cioè dell'energia di legame tra i protoni ed i neutroni che formano il nucleo. L'energia di legame tra i nucleoni è misurata dall'energia che bisognerebbe spendere per separare i nucleoni stessi ed ottenerli isolati allo stato in quiete. La sua relazione col difetto di massa discende dalla legge della equivalenza tra massa ed energia
espressa dalla fondamentale relazione relativistica di Einstein: per essa, ad ogni variazione di massa ∆m è associata una variazione di energia:
∆E=∆m * c2
È quindi evidente che dal difetto di massa è immediatamente individuabile l'energia di legame tra i nucleoni di un nucleo. È necessario però stabilire il rapporto di equivalenza tra massa ed energia:
(E) 1 u.m.a. = (3*1010)2 * 1,66*10-24 = 1,495*10-3 erg = 933 MeV
L'energia di legame tra i nucleoni, espressa in MeV, si calcola quindi dai difetti di massa, espressi in u.m.a., moltiplicandoli per
questo rapporto di conversione:
E=933 * ∆m
Particolarmente significativa per una valutazione della stabilità dei nuclei, più che l'energia totale di legame è l'energia di legame media per nucleone ([Enucl]) che si ottiene dividendo l'energia
totale calcolata dal difetto di massa per il numero di nucleoni componenti il nucleo, ossia per il
numero di massa A. Consideriamo il diagramma che esprime l'energia di legame media in funzione del numero di massa. Se si esclude il primo tratto della curva, relativa ai nuclei più leggeri, per i quali l'energia di legame cresce rapidamente col numero di massa, la curva è caratterizzata da un andamento pressoché parallelo all'asse delle ascisse corrispondente ad un valore medio dell'energia di legame media per nucleone di circa 8MeV e declina poi molto moderatamente per i nuclei pesanti. Mediamente insomma, se si escludono i nuclei più leggeri, risulta in prima approssimazione
[Enucl]=cost ⇒
E nucl
=cost ⇒ Enucl = cost * A
A
15
cioè l'energia totale di legame è approssimativamente proporzionale al numero di nucleoni. Da questo si arguisce che le forze
che tengono legati tra loro i nucleoni sono forze a corto raggio d'azione, perché se così non fosse, Enucl dovrebbe essere proporzionale ad A*(A-1), perché dovrebbe tenere conto anche di tutti gli altri nucleoni. Nella figura He4, C12 ed O16 sono picchi
di stabilità (costituiti da 1, 3 e 4 particelle α). Il massimo di stabilità si ha attorno al ferro. In conclusione abbiamo visto che a
tenere unito il nucleo è l'interazione nucleare forte. Si noti però che questa ha un corto raggio d'azione, dell'ordine di 10-15 m
(unità di misura detta Fermi). Se due nucleoni sono distanziati anche solo da 1 o 2 Fermi, la forza nucleare forte scende rapidamente a zero. Inoltre, l'interazione tra i nucleoni, nel caso della nucleare forte, è indipendente dalla carica. Possiamo allora
fare un modellino del nucleo, detto modello a goccia. Prendiamo una goccia d'acqua: le varie
molecole di H2O subiscono la forza di Van Der Waals (di tipo elettromagnetica). Secondo questa forza, ogni molecola interagisce solo con le sue vicine. In tal modo le molecole sono attratte
verso il centro e si crea la forza di superficie che tiene in coesione la goccia. Se la goccia pesa
troppo, la forza di gravità la farà allungare, fino a quando questa sopravvarrà su quella di Van
Der Waals.
Prendiamo ora un nucleo. I nucleoni interagiscono solo con gli immediati vicini. Questo genera
una tensione che tiene compatto il nucleo. Al posto delle forze di Van Der Waals avremo l'interazione nucleare forte. È molto importante il rapporto protoni/neutroni. La stabilità nucleare, infatti, dipende proprio da questo. Chiudiamo con una curiosità: 1 cm3 di materia nucleare peserebbe 100'000'000 di tonnellate, a conferma dell'enorme densità della materia nucleare, paragonabile ai buchi neri.
Tipi diversi di reazioni nucleari a bassa energia (<100MeV)
I.
II.
III.
Reazioni prodotte da α:
Reazioni prodotte da p:
Reazioni prodotte da γ:
(α,p) = N147 (α,p) O178
(p,α) = Li73 (p,α) He42
(γ,n) = H2
(γ,n) H1
(α,n) = Be94 (α,n) C136
Schema delle reazioni a bassa energia
Il tempo di vita media del nucleo composto è di circa 10-14 secondi.
Reazioni prodotte da neutroni
Sono molto importanti (basti pensare ai reattori nucleari). Possono essere di diverso tipo: (n,α), (n,p), (n,γ), (α,n).
Ad esempio:
U238 (nv,α) ⇒ U237 ⇒ β- ⇒ Np239 ⇒ β- ⇒ Pn239
238
U (α,n) ⇒ Pn241 ⇒ Famiglia Np237 (T½=2,2*106 anni)
Tutti gli elementi con Z>92 sono artificiali.
Fissione nucleare
La fissione è una reazione nucleare che si ha solo per i nuclei ad elevato numero atomico (Z>82): un nucleo colpito da un neutrone lo assorbe ed immediatamente si spezza in due nuclei di medio numero atomico rilasciando 2 o 3 neutroni liberi. Il fatto
che nella reazione si generino due nuclei di medio numero atomico è la differenza sostanziale che distingue la fissione dalle altre reazioni nucleari nelle quali si generano dei frammenti di particelle subnucleari. La probabilità della fissione spontanea è
estremamente piccola. Si può però provocarla bombardando certi nuclei pesanti con particelle aventi energia sufficientemente
16
alta. Prima di studiarla in dettaglio analizziamo il rallentamento dei neutroni. Il neutrone emesso dalla sorgente è ancora veloce. Facendolo passare attraverso dell'acqua, però, esso subisce degli urti contro le molecole di H2O, cedendo ad esse energia
cinetica e quindi rallentandosi. Dopo poche decine di urti l'energia del neutrone passa a 0,1MeV che è l'energia media delle
molecole di H2O. A questo punto l'originario neutrone veloce è divenuto un neutrone termico (o neutrone lento). I neutroni
termici sono importanti, perché permettono una resa molto maggiore nella fissione. Ad esempio:
U235 + nt ⇒ Sn127 + Mo105 + 4nv
U235 + nt ⇒ Te136 + Zr97 + 3 nv
Il neutrone spacca l'uranio 235 in due parti di massa circa uguale. Ci possono essere una quarantina di fissioni diverse, con formazione di 200 isotopi radioattivi. Mediamente in una fissione si formano 2 o 5 nv (comunque sempre più di uno).
Modello di fissione basato sul modello a "goccia"
Soglia di fissione
Per portare il nucleo nello stato di pre-sissione, devo spendere lavoro Sf. Una parte di questo è fornito dal neutrone che passando vicino al nucleo viene risucchiato dalla forza nucleare forte. Se Wn è il lavoro fatto dal neutrone, ho che Sf=(L - Wn) dove
L è il lavoro totale che devo spendere. Ci sono isotopi che hanno Sf<0 ( U235, U237, U239 detti isotopi fissili). Tali isotopi si
possono fissionare anche con neutroni lenti che hanno il vantaggio, rispetto ai neutroni veloci, di un'elevata resa. Questo perché
i neutroni termici passano più vicino al nucleo e per più tempo, in maniera tale che la forza nucleare forte riesce più spesso a
risucchiarli. Per l'uranio 235, l'energia sviluppata è di circa 200MeV (circa 2*1010 Kcal/Kg). Abbiamo detto che nel processo di
fissione vengono liberati due o tre neutroni i quali, a loro volta, interagendo con altri nuclei, possono provocare altre fissioni.
Così la reazione procede con un meccanismo a catena. Tale condizione però si verifica solo se la massa del materiale fissile
supera un determinato valore critico. A questo punto la reazione si mantiene da sé. Se poi essa avviene in modo tale che il numero di neutroni si moltiplica col procedere degli atti individuali di fissione, la sua velocità aumenta rapidamente, così da renderla esplosiva. Introducendo, però, degli adatti assorbitori di neutroni, è possibile controllare la velocità del processo ed utilizzare il calore sviluppato. Quindi chiamo massa critica un valore di massa sufficiente per essere sicuri che tutti i neutroni in entrata non escano prima di avere compiuto la fissione.
Principi di funzionamento dei reattori nucleari
1.
2.
Reattori termici: La fissione è prodotta da neutroni termici. Essi si dividono in:
a)
Reattori ad uranio naturale: i nuclei sono solo lo 0,715% ( U235 ), per cui siamo al di sotto della massa critica
e non c'è rischio di reazione nucleare a catena. Anzi, avendo pochi nuclei fissili, il reattore tende a spegnersi.
Come moderatore si usa D2O (acqua pesante) o della grafite. Chiamiamo K il fattore di moltiplicazione neutronica. (in genere K=1). Se K>1 ⇒ si ha il cosiddetto stato critico. Se K<1 ⇒ il reattore tende a spegnersi.
Normalmente si tiene K>1 (anche se di poco) così si entra leggermente in stato critico e si gestisce l'eccesso
di neutroni con apposite barre di controllo al cadmio (che li assorbe). Se la temperatura si alza troppo, i nuclei possono fondere, il refrigeratore evapora e si scinde in idrogeno ed ossigeno che si incendiano. Sono
quindi indispensabili ottimi sistemi di controllo.
b)
Reattori ad uranio arricchito: La percentuale di nuclei fissili è portata al 2-4% (U235 ) e come moderatore si
utilizza H2O. L'acqua è un assorbitore di neutroni, ma il numero di questi è comunque sufficiente per attivare
la reazione. L'acqua funge anche da refrigeratore, ma viene pressurizzata (140 atm.) per aumentare il punto di
ebollizione. Da ciò deriva il nome di queste centrali: PWR (da Pressurized Water Reaction).
Reattori veloci: La fissione è prodotta da neutroni veloci. Si noti che in questi reattori c'è assenza di moderatori e come
refrigeratore si usa Na liquido. Dato che il rendimento coi nv è minore, aumenta la concentrazione dei nuclei fissili. In
certe condizioni, il reattore produce più quantità di elementi fissili di quello che usa. Questi reattori lavorano in condizioni più critiche degli altri (temperatura ed influenza neutronica maggiori) e proprio per i rischi che comportano sono
stati gradualmente abbandonati.
17
Le scorie
Le scorie derivano dai 200 nuclidi radioattivi cui abbiamo accennato prima. Ebbene i nuclidi radioattivi spesso possono avere
un tempo di dimezzamento di 20000 e più anni. C'è chi dice che le scorie si possono trattare, ma ciò appare oggi quasi impossibile.
La fusione nucleare
La fusione è il processo di combinazione di due nuclei leggeri che, fondendosi l'uno con l'altro, danno origine ad un nucleo più
pesante. Questo processo è accompagnato dalla liberazione di una quantità di energia molto più alta di quella sviluppata nel
processo di fusione. Distinguiamo tra reazioni esotermiche (liberano energia) ed endotermiche (assorbono energia). Se avvicino
due protoni, c'è una repulsione. Quindi come faccio ad arrivare ad una fusione ? Devo riuscire ad avvicinarli talmente tanto da
far intervenire la forza nucleare forte. Devo cioè superare la barriera di Coulomb (forza repulsiva) per portare i nuclei alla distanza di alcuni Fermi. Ma per fare ciò, i nucleoni devono essere spinti l'uno contro l'altro ad alta velocità. Un parametro importante è la sezione d'urto σ, che misura la probabilità di realizzazione del processo di fusione. Normalmente è in funzione della
velocità. Se la velocità è bassa, la fusione non avviene, ma anche se la velocità è troppo elevata la resa sarà minore, perché i
nucleoni non avranno tempo per reagire.
Fusione termonucleare
Le seguenti sono le fusioni nucleari che avvengono all'interno del Sole:
Reazione
Energia in gioco(MeV)
0,42
H 1 + H1 ⇒ H2 + β + + n
1
3
5,5
H + D ⇒ He + n
12,8
He3 + He3 ⇒ He4 + 2H1
Potere calorifico (1010 cal/Kg)
0,49
4,2
5,0
Le seguenti sono invece reazioni usate nella bomba H:
Reazione
Energia in gioco(MeV)
17,6
D + T ⇒ He4 + n
11,4
T + T ⇒ He4 + 2n
Potere calorifico (1010 cal/Kg)
8,1
4,4
La reazione D+T ⇒ He4 + n è una reazione molto importante perché è quella che viene utilizzata negli esperimenti per la produzione di energia elettrica. Tuttavia questa reazione non avviene semplicemente accostando i due elementi. È necessario utilizzare il plasma termonucleare ad altissima temperatura (si tratta di una miscela in cui ogni elettrone è stato sbalzato via dal
proprio nucleo.)
Bilancio energetico
Per quel che riguarda il bilancio energetico, l'energia liberata dal processo di fusione, meno quella usata come irraggiamento ed
emissione di neutroni, deve essere maggiore di quella che somministro per tenere confinato ed in temperatura il plasma.
18
Criterio di Lawson
n * t >= f(T,h)
dove t è il tempo di confinamento, f una funzione che varia da reazione a reazione e h è l'efficienza con cui l'energia prodotta
può essere utilizzata per tenere viva la reazione. Se ciò si verifica, abbiamo raggiunto il punto di pareggio, dove il bilancio energetico è zero, visto che l'energia che ottengo è uguale a quella che uso per tenere vivo il processo). Nelle stelle, il confinamento avviene in maniera naturale grazie alla forza di gravità. Artificialmente il confinamento del plasma avviene in due modi:
I.
confinamento inerziale mediante fasci laser e ioni;
II. confinamento magnetico mediante l'uso di forti campi magnetici.
Il plasma viene immesso all'interno di un toroide cavo. Il problema sta nel non fargli toccare le pareti, visto che la temperatura
è elevatissima, altrimenti le rovinerebbe e si raffredderebbe. Per controllarlo si usano allora campi magnetici che vengono creati grazie ad elettromagneti e superconduttori a temperatura dell'elio liquido. (4-5 K). I campi magnetici usati sono diversi. Il
progetto che produce corrente massima è il tokamak: il campo magnetico è concentrato al centro dell'anello, poi un campo indotto secondario fa passare la corrente in circolo all'anello. Per effetto Joule la temperatura si alza fino a raggiungere un valore
massimo. Lo sfruttamento della fusione nucleare pone numerosi problemi da risolvere. Il plasma deve essere confinato, anche
se tende ad espandersi. Inoltre come sfruttare l'eventuale energia che si produrrebbe ? L'energia utilizzabile sarebbe quella del
neutrone espulso durante la reazione (14,06 MeV). Il calore prodotto potrebbe alimentare turboalternatori esterni. Inoltre il trizio non esiste in natura e lo si dovrebbe sintetizzare con la reazione tra il litio ed il neutrone veloce, senza produzione di scorie,
ma con ben altri problemi: il flusso neutronico sarebbe talmente alto che solo dei robot potrebbero mettere piede nella centrale.
Inoltre il trizio, essendo molto diffusivo, tenderebbe ad espandersi molto. Infine i neutroni prodotti interagirebbero anche col
reticolo cristallino dei materiali che rivestono le pareti del toroide, cambiando così le loro caratteristiche e rendendo necessario
l'utilizzo di materiali impermeabili ai neutroni.
Processo di nucleosintesi degli elementi nei corpi stellari
Come si sono formati gli elementi? Mentre nel caso del toroide è necessario utilizzare campi magnetici per contenere il plasma,
nelle stelle ci pensa la forza di gravità: all'inizio una stella si forma dalla condensazione di una nube di idrogeno. Mano a mano
che la stella collassa, la temperatura si alza, fino a raggiungere la temperatura di fusione dell'idrogeno. Le reazioni di fusione
contrastano la gravità e fermano quindi il collasso. Quando tutto l'idrogeno si sarà fuso in elio, il collasso riprenderà e la temperatura tornerà ad alzarsi fino a raggiungere la temperatura di fusione dell'elio. Il ciclo continuerà fino ad arrivare al ferro quando il collasso continuerà indisturbato perché le reazioni seguenti saranno endotermiche.
19
La struttura elettronica degli elementi e la loro classificazione periodica
La nascita della teoria dei quanti
Il modello atomico planetario proposto da Rutherford risultava incompatibile con le leggi classiche: secondo queste una carica
elettrica che si muova con moto non rettilineo ed uniforme irradia energia sotto forma di onde elettromagnetiche, sicché un elettrone rotante nell'atomo attorno al nucleo, irradiando onde della stessa frequenza del suo moto di rivoluzione, subirebbe una
progressiva diminuzione della propria energia, cadendo inesorabilmente sul nucleo con un moto a spirale in un tempo dell'ordine del 10-11 secondi. Inoltre col progressivo avvicinarsi dell'elettrone al nucleo, ossia col progressivo ridursi delle dimensioni
dell'orbita e con la conseguente variazione della frequenza del moto di rivoluzione, si verificherebbe anche una variazione continua della radiazione emessa e non sarebbe perciò interpretabile l'emissione di spettri costituiti da righe di frequenza definita e
costante. Gli studi di taluni fenomeni inerenti l'origine dell'emissione e dell'assorbimento delle radiazioni da parte dei corpi, rese manifesta l'esigenza di ricorrere a leggi nuove, non conformi a quelle classiche. Vediamo di vedere le considerazioni fatte
ancora con le leggi classiche. Tra i costituenti fondamentali degli atomi erano stati da tempo individuati gli elettroni: questi,
muovendosi entro gli atomi con moto non rettilineo ed uniforme, determinerebbero l'emissione di radiazioni. Gli elettroni in
moto sarebbero così da riguardare come emettitori elementari, microscopici, i cui effetti, sommandosi si osserverebbero come
radiazioni di varia frequenza ed intensità variabile. Di più, essi si potrebbero descrivere come altrettanti oscillatori, considerando gli elettroni ai quali va attribuita l'emissione in condizioni tali da compiere oscillazioni di tipo armonico di ben determinata frequenza attorno a definite posizioni di equilibrio attorno agli atomi (con riferimento ancora al modello di Thomson). Le
radiazioni emesse sarebbero allora caratterizzate dalla stessa frequenza di questi oscillatori elementari, e nello spettro di emissione di un corpo ogni riga di ben definita frequenza sarebbe da attribuire ad una famiglia di oscillatori elettronici, tutti oscillanti con quella stessa frequenza. Quando una radiazione penetra in un corpo, secondo questo disegno, ecciterebbe gli elettroni
in esso contenuti ad oscillare con la stessa frequenza delle onde elettromagnetiche che compongono la radiazione incidente. Essi perciò si tramuterebbero in emettitori di un'onda elettromagnetica di quella frequenza, propagantisi in tutte le direzioni. Da
ciò la diffusione. D'altro canto gli elettroni così eccitati dalla radiazione incidente provocherebbero col loro moto un aumento
dell'agitazione termica degli atomi di un corpo, così che parte dell'energia della radiazione si trasformerebbe in calore. Questi i
lineamenti della teoria elettronica di Lorentz. Ma una descrizione di questo tipo, quando la si voglia completare e precisare in
senso quantitativo, porta i diversi fenomeni a conclusioni totalmente inconsistenti coi dati sperimentali. Un esempio particolarmente significativo ci è fornito dallo spettro del corpo nero. Ogni corpo solido a qualunque temperatura emette radiazioni a
spettro continuo che, invisibili a temperatura ordinaria perché di lunghezze d'onda che cadono nell'ultrarosso, divengono visibili elevando la temperatura a diverse centinaia di gradi (si dice che il corpo è portato all'incandescenza). L'intensità delle radiazioni emesse dipende dalla temperatura e varia con la lunghezza d'onda in modo diverso secondo la natura della sostanza considerata. Però se il corpo emittente da questa formato è un corpo nero, cioè tale che assorba totalmente l'energia raggiante che
lo investe, lo spettro risulta indipendente dalla natura della sostanza e dalla forma del corpo. Tracciando per diverse temperature l'andamento dell'intensità I della radiazione emessa in funzione della frequenza n, si hanno curve del tipo riportato con tratto
pieno: esse presentano un massimo che col crescere di T si sposta verso le maggiori frequenze. L'elettromagnetismo classico
ricondurrebbe l'emissione del corpo nero agli oscillatori elettronici elementari in esso contenuti: lo spettro emesso risulterebbe
continuo, avendosi da considerare per le frequenze degli oscillatori elementari tutti i valori possibili, variabili con continuità. Si
perverrebbe in tal modo all'equazione I =
2πkT 2
ν , cioè ad una parabola. Una curva di questo tipo mentre si approssima alc2
l'andamento sperimentale nel campo delle frequenze basse, se ne discosta sempre più nettamente con l'aumentare della frequenza, tendendo all'infinito. Come conseguenza di ciò risulterebbe infinita l'intensità totale di emissione, il che è ovviamente assurda. Fu studiando questo problema che Max Plank introdusse un nuovo concetto: fintantoché si ammetteva che l'energia emessa
dal singolo oscillatore elementare potesse avere un valore qualunque, variabile con continuità da un atto di emissione ad un altro, non si poteva fare altro che giungere all'assurdo precedente. Mentre si giungeva ai risultati concordi con l'esperienza se si
supponeva che ogni oscillatore potesse assorbire od emettere solo quantità di energia che fossero multiple intere di una quantità
minima e finita ε, caratteristica di ogni oscillatore, ossia ammettendo che ogni oscillatore elementare potesse emettere o assorbire energia solo per salti successivi della grandezza ε, e quindi con discontinuità:
ε=h*ν
dove h=6,625 * 10-27 erg * Sec è la costante di Plank. L'espressione dell'intensità in funzione della frequenza diviene:
I=
2πkT
*
c2
hν
e
hν
kT
−1
La costante di Plank rappresenta il minimo valore che può assumere l'azione in un fenomeno meccanico: questa in ogni caso
può assumere solo valori che siano multipli interi di quello, e quindi può variare solo con discontinuità, potendo incrementarsi
solo per quantità discrete o quanti, assai piccoli ma finiti. Per questa h è detta quanto d'azione. È proprio qui che si realizzò il
primo distacco dalle leggi della fisica classica, con l'ipotesi fondamentale di una discontinuità che nelle leggi, applicate a feno20
meni macroscopici, facevano prevedere. La quantizzazione dell'azione porta con sé la quantizzazione dell'energia. Se h rappresenta il quanto d'azione, ε = h * ν rappresenta il quanto d'energia dell'oscillatore.
Effetto Fotoelettrico
Secondo lo studio dell'effetto fotoelettrico, molti corpi se colpiti da radiazioni elettromagnetiche di frequenza sufficientemente
alta, emettono degli elettroni. L'emissione degli elettroni si verifica solo se la frequenza della radiazione incidente è più alta di
un valore minimo ν0 detto soglia fotoelettrica. Gli elettroni emessi, detti fotoelettroni, hanno velocità diverse e quindi energie
diverse. Il valore massimo dell'energia cinetica dipende dalla frequenza dell'onda incidente secondo la relazione di Einstein:
Emax = h*(ν - ν0)
Secondo le leggi classiche, la radiazione incidente, colpendo la superficie del corpo, investe gli elettroni degli atomi superficiali
che, essendo sottoposti al campo alternato dell'onda elettromagnetica della radiazione, vengono sollecitati ad oscillare. Se le
oscillazioni degli elettroni sono molto ampie, essi possono essere strappati dagli atomi. Tuttavia le leggi classiche non rendono
conto dell'aspetto quantitativo del fenomeno, infatti la velocità degli elettroni espulsi dovrebbe crescere con l'intensità del campo elettrico che ne provoca l'espulsione, ma questo non corrisponde ai risultati dell'esperienza, secondo cui l'energia cinetica
massima dei fotoelettroni è costante.
Leggi dell'effetto fotoelettrico
I.
Il fenomeno si verifica se e solo se ν>ν0 (ν0 = soglia fotoelettrica)
II.
Emax = h * (ν−ν0)
III.
Nfotoelettroni = cost * I
Per quanto detto sopra, non possiamo utilizzare le leggi classiche perché arriveremmo a degli assurdi. Einstein, completando la
teoria di Plank dell'emissione quantizzata di una radiazione, secondo la quale l'energia emessa corrisponde sempre ad un numero intero di quanti hν, concepì la radiazione come costituita da granuli elementari detti quanti di luce o fotoni trasportanti ciascuno l'energia E=hν. Un fotone, investendo un atomo del corpo irradiato, gli trasferisce la quantità di energia hν che porta con
sé, e se questa è maggiore dell'energia E0 necessaria per strappare l'elettrone, un elettrone viene liberato o espulso. Quindi l'emissione di elettroni può verificarsi solo se hν>E0, cioè se la frequenza della radiazione incidente è maggiore di E0/h. L'energia
cinetica dell'elettrone emesso risulterà uguale alla differenza hν-E0. Inoltre, col variare dell'intensità della radiazione incidente,
varia il numero di fotoni che colpiscono la superficie del corpo, ma non la loro energia, che è costante, così che al diminuire
dell'intensità varia solo il numero di elettroni espulsi. Quindi l'emissione di elettroni nell'effetto fotoelettrico è dovuto ad un urto tra elettrone e fotone. Chiamiamo E0 l'energia di legame di e-:
hν0=E0 ⇒ ν0 =
E0
⇒ Frequenza di soglia (dimostra la I.)
h
hν0>E0 ⇒ ∆E=hν-hν0 = h * (ν-ν0) ⇒ (dimostra la II.)
Le formule relativistiche viste ci danno una caratterizzazione del fotone, "granulo di energia", ma dato che E ed m sono in relazione:
Efotone=Ecin+Eintrinseca =
m 0c 2
1−
v2
c2
2


Moltiplicando membro a membro per la quantità  1 − v  , si ottiene:
2

c 
2


Efotone *  1 − v  = m0 * c2
2
c 

Essendo, per il fotone, v=c, l'equazione diventa:
Efotone * (1-1) = m0 * c2 = 0
Per cui si ottiene m0 = 0, cioè il fotone ha massa a riposo nulla. Tutta la sua massa (o meglio la quantità di moto) la acquista
muovendosi a velocità c. Questa quantità di moto può infine cederla quanto si scontra con un elettrone. La quantità di moto del
fotone sarà:
Etot = c * p 2 + m 0 c 2 ⇒ E = c * p
Per cui:
p=
E hν
h
=
⇒p=
c
c
λ
I fotoni con una piccola lunghezza d'onda hanno quindi una maggiore quantità di moto e quindi maggiore potere penetrante (
come i raggi X o i raggi γ ).
21
Spettri di emissione caratteristici degli atomi
La fonte più preziosa di notizie sulla struttura elettronica degli atomi è costituita dai loro spettri
di emissione. È noto che l'energia raggiante, ed in
particolare quella luminosa, si propaga nello spazio per onde, di natura elettromagnetica, caratterizzate dalla variazione periodica del campo elettrico e del campo magnetico fra loro mutuamente
perpendicolari ed entrambi funzioni sinusoidali
del tempo e dello spazio percorso (considerando
radiazioni piane monocromatiche: piane in quanto
si assume che, a grande distanza, la direzione di
propagazione sia perpendicolare al fronte d'onda,
monocromatica, perché tutte della stessa lunghezza d'onda). Queste onde si possono rappresentare come in figura. Chiamiamo
~ il numero di lunghezze d'onda contenute nell'unità di lunghezza, ossia il centimetro. Dicendo c la velocità di
numero d'onde ν
propagazione dell'onda, si ha:
λ=c τ =
c
c
~ = 1 =ν
⇒ν= ⇒ ν
λ
λ c
ν
L'unità di misura di λ è l'Amstrong ( 1 Å = 10-8 cm. ) e per la ν si usa l'Hertz. Abbiamo accertato che l'energia luminosa si propaga per onde di natura elettromagnetica: vanno distinti, però, il termine luce ed energia raggiante. Col primo termine si suole
indicare l'insieme di onde elettromagnetiche (e perciò di energia raggiante) che l'occhio umano normalmente riesce a cogliere,
essendo radiazioni visibili. È opportuno avere ben chiaro sin d'ora che il campo visibile delle radiazioni è solo una porzione
limitatissima di tutto l'insieme delle onde elettromagnetiche, estendendosi soltanto da circa 4000Å fino a circa 7500Å. La regione nella quale cadono gli spettri atomici ottici degli elementi si estende dall'infrarosso, attraverso tutto il visibile ed arriva
fino all'ultravioletto.
L'analisi della composizione spettrale emessa
da una qualunque sorgente, o di quelle assorbite quando un fascio di radiazioni a spettro continuo attraversi un corpo materiale, è il mezzo
fondamentale con cui la spettroscopia dà il suo
maggior contributo. Si parla di spettroscopia di
emissione e di assorbimento. L'indagine spettroscopica si avvale di strumenti atti ad analizzare l'insieme delle radiazioni di diversa lunghezza d'onda emesse o assorbite da un corpo o
una sostanza. Lo spettroscopio è in questo caso
costituito da un prisma che scinde le diverse componenti del fascio di radiazioni analizzato. Il fascio divergente di raggi che
provengono dalla fenditura deve essere parallelo prima di incidere sull'elemento dispersivo. A ciò provvede, negli strumenti a
prisma, un'apposita lente collimatrice. Le radiazioni trasmesse dal prisma, diversamente deviate secondo la loro lunghezza
d'onda, sono focalizzate sulla lastra fotografica mediante una seconda lente. È noto che quando un corpo solido è portato all'incandescenza, esso emette un insieme di radiazioni luminose costituenti, all'esame spettroscopico, uno spettro, mentre i gas ed i
vapori emettono radiazioni costituite da serie, spesso a struttura molto complessa, di righe distinte o di bande che corrispondono a lunghezza d'onda ben determinate. Gli spettri di righe sono emessi di solito dagli atomi singoli, isolati l'uno all'altro, e per
questo sono detti spettri atomici, mentre gli spettri di bande derivano da aggregati stabili di atomi e perciò sono detti spettri
molecolari.
Spettri caratteristici dell'atomo di idrogeno
La complessità degli spettri atomici dipende strettamente
dalla complessità della struttura elettronica degli atomi, e
quindi varia entro i più larghi limiti. Consideriamo lo spettro dell'idrogeno, il più semplice. In esso vi si rilevano più
serie di righe in ognuna delle quali la separazione tra riga e
riga e l'intensità vanno progressivamente decrescendo verso le minori lunghezze d'onda, così che le successive componenti di ogni serie risultano notevolmente distanziate
verso l'estremo della serie corrispondente alle più grandi
lunghezze d'onda, mentre, infittendosi sempre più a mano a
22
mano che la lunghezza d'onda diminuisce, tendono ad un netto limite di convergenza verso l'opposto estremo. La prima ad essere studiata tra le serie spettrali dell'idrogeno fu quella che cade nella regione del visibile e nel vicino ultravioletto, detta serie
di Balmer, di equazione:
λ= k*
n2
n −4
2
che può essere scritta nella forma assai più significativa:
1 ~ ν
1 
 1
= ν = = ℜH *  2 − 2 
λ
n 
c
2
~ è il numero d'onde proprio della riga spettrale considerata.
dove ν
La costante ℜH è detta costante di Rydberg e vale: ℜH = 109667,76 cm-1. Da questa equazione di può determinare anche il limite di convergenza della serie di Balmer:
~ = ℜ H = 27419,45 cm-1 ⇒ λ= 3647,05 Å
ν
4
Accanto a quella di Balmer si osservano nello spettro dell’idrogeno altre serie di righe nell'ultravioletto e nell'ultrarosso. Lo
spettro dell'idrogeno atomico è in conclusione descrivibile dalla equazione:
1 
~ =ℜ * 1
ν
H
 2 − 2
 ns
Nome della serie
Lyman
Balmer
Paschen
Brackett
Pfund
ns
1
2
3
4
5
n
2,3,4,...
3,4,5,...
4,5,6,...
5,6,7,...
6,7,8,...
n 
dove ns rappresenta il tipo di serie ed n individua una singola riga all'interno di
questa serie. Nello spettro dell'idrogeno è agevole cosa l'identificazione delle varie
serie, ma per atomi meno semplici, le difficoltà sono spesso molto grandi, perché
appaiono anche le righe derivanti dalle diverse forme ionizzate. Vari sono i criteri
che possono aiutare: tutte le righe di una stessa serie, sotto l'azione di un forte
campo magnetico, si risolvono, cioè si scindono nello stesso modo in date componenti. Questo effetto è noto come effetto Zeeman.
Spettri dei sistemi idrogenoidi
Gli spettri più simili a quelli dell'idrogeno, per la loro semplicità, sono quelli dei sistemi idrogenoidi, cioè atomi ionizzati a tal
punto da conservare attorno al nucleo un solo elettrone, riproducendo così la struttura elettronica dell'atomo di idrogeno. Nello
ione idrogenoide, l'elettrone residuo ruota attorno al nucleo con carica Ze, dove Z è il numero atomico. Gli spettri di emissione
dei sistemi idrogenoidi sono costituiti da serie di righe descritte dall'equazione
~ = Z2 * ℜ *  1 − 1 
ν
 2
H
2 
nr 
 ns
Il numero di onde proprio di ciascuna riga dello spettro dell'idrogeno atomico è calcolabile come differenza tra due termini, di
cui uno, il primo, è costante per le righe di una stessa serie, mentre il secondo è variabile da riga a riga. Essi sono nella forma
τ(n) =
ℜH
n2
e sono chiamati termini spettrali. Anche per sistemi idrogenoidi il numero di onde delle loro righe spettrali è calcolabile come
differenza tra due termini:
~ s,i=τs − τi
ν
dove τs è un termine costante per ciascuna serie e diverso da serie a serie (termine di serie), τi varia entro ogni serie da riga a
riga (termine corrente).
Principio di combinazione di Rydberg e Ritz
Il numero di onde relative ad una qualunque riga nello spettro di un elemento è espresso dalla combinazione di due termini
spettrali propri dell'elemento stesso. Sommando o sottraendo tra loro le frequenze di due righe di uno spettro, si ottiene la frequenza di un'altra riga dello stesso spettro.
23
I raggi X ed il loro spettro
Nel 1895 il fisico Röntgen osservò per la prima volta che
quando un fascio di raggi catodici prodotti in uno dei soliti tubi a scarica, ad alto vuoto, incide su una qualunque
superficie materiale, che può essere la parete stessa del
tubo oppure un qualunque corpo in esso introdotto, a cui
si dà il nome generico di anticatodo. Si genera un nuovo
tipo di radiazioni, che furono dette raggi X perché di natura allora incognita. Le radiazioni emesse dall'anticatodo
bersagliato dagli elettroni incidenti su di esso ad alta energia cinetica, sono della stessa natura delle radiazioni
luminose, cioè sono radiazioni elettromagnetiche: esse
hanno lunghezza d'onda assai piccola, e quindi un alto potere penetrante. Essendo più piccola la lunghezza d'onda,
risulterà più alta la frequenza e corrispondentemente risulterà più grande il valore dell'energia trasportata dai fotoni che la compongono. Di particolare interesse si presenta l'analisi dei
raggi X emessi da anticatodi di materiali diversi: come elemento dispersivo si usa, al posto del prisma, un cristallo, in quanto la
distanza fra le molecole nel reticolo cristallino è tale da potere essere paragonata alla lunghezza d'onda del raggio. In questa
maniera lo stesso raggio sarà rifratto a seconda della frequenza che possiede. Analizzando con uno spettrografo di questo tipo
(spettrografo di Bragg) i raggi X emessi da un tubo generatore, lo spettro che si registra risulta costituito di regola dalla sovrapposizione di uno spettro continuo e di uno spettro discontinuo di righe. Lo spettro continuo presenta un termine netto dalla
parte delle più alte frequenze (minori lunghezze d'onda) e degrada invece sfumando verso la parte opposta delle frequenze più
basse. Questo comportamento trae origine dal progressivo frenamento degli elettroni incidenti sull'anticatodo per effetto degli
urti con gli atomi dell'anticatodo stesso. Tale progressivo frenamento determina un'accelerazione negativa degli elettroni, che
perciò irradiano onde elettromagnetiche. Sono queste onde che costituiscono lo spettro continuo, detto radiazione di frenamento. Lo spettro di righe sovrapposto a quello continuo, come si è detto, varia al variare della specifica natura dell'anticatodo: esso
è detto spettro Röntgen di emissione. Anche le righe degli spettri Röntgen, come quello degli spettri ottici sono raggruppate
molto evidentemente in serie, formate però da poche righe soltanto: si designano con le notazioni K, L, M, N, ... in ordine di
frequenza decrescente. Per ogni serie le frequenze (numeri d'onda) delle righe componenti si possono calcolare come differenza
di due termini. Essi variano con uniforme regolarità: all'aumentare del numero atomico dell'elemento, si osserva che passando
da un elemento al successivo lo spettro conserva lo stesso aspetto generale, mentre si nota uno spostamento di tutte le sue righe
verso le maggiori frequenze (ossia verso le minori lunghezze d'onda). Per gli elementi con basso numero atomico si osserva solo la serie K ( da Z=8 ). Successivamente compare la serie L (da Z=23) e di seguito tutte le altre. Col crescere del numero atomico si osserva anche un progressivo aumento del numero di righe entro ciascuna serie. Inoltre vengono emesse solo le serie le
cui righe hanno frequenze inferiori a quella corrispondente al limite dello spettro continuo (ν0), ossia lo spettro di righe osservabile risulta sempre totalmente sovrapposto allo spettro continuo. Entro ciascuna serie le singole componenti sono designate
con gli indici α, β, ... Nel 1913 Moseley mise in evidenza che le frequenze caratteristiche delle righe corrispondenti di ciascuna
serie emesse da elementi diversi sono legate al numero atomico Z degli elementi stessi da una legge che prese il suo nome (legge di Moseley):
ν = a * (Z - σ)
dove a è una costante di proporzionalità diversa da serie a serie e anche da riga a riga della stessa serie e σ è costante per le righe di una data serie. Per K si ha σ=1, per L si ha σ=7, 4, ... Dunque la radice quadrata della frequenza di righe corrispondenti (
Kα, Lα oppure Mα) emesse dai diversi elementi, risulta proporzionale al numero atomico dell'elemento considerato. La legge di
Moseley ha chiarito le inversioni nella classificazione periodica degli elementi.
Modello di Bohr dell'atomo di idrogeno
Secondo il primo disegno datone da Bohr, derivandolo dal modello di Rutherford, l'atomo di idrogeno sarebbe da concepire
costituito da un nucleo centrale positivo, attorno al quale un elettrone ruota descrivendo, secondo le leggi meccaniche classiche,
un'orbita ellittica o, in particolare, circolare. L'unica legge da soddisfare è quella della dinamica F=ma che, in questo caso, impone che la forza elettrone-nucleo e2/r2 (forza di Coulomb) eguagli il prodotto della massa per l'accelerazione centripeta:
e2
v2
m
=
r
r2
da cui:
r=
e2
mv 2
v=
e
mr
Dunque, secondo le leggi classiche, il raggio dell'orbita sarebbe funzione solo della velocità di rotazione. Quindi non c'è nessuna limitazione per l'energia E dell'elettrone.
24
2
e 
e2 1 e2 e2
1 e2
−
=
−
=
−

r
2 r
r
2 r
 mv 
2
ET = EC + EP = 1 mv 2 − e = 1 m * 

2
r
2
Questa l'impostazione classica del modello di Bohr. Per superare le difficoltà viste, Bohr innestò su queste basi ancora fondate
sulla meccanica classica, un postulato restrittivo, ad essa del tutto estranea.
1° Postulato: Il valore del momento della quantità di moto dell'elettrone rotante rispetto al nucleo deve essere un multi•
plo intero della quantità h/2π.
mvr = n *
h
2π
Questo è noto come postulato della quantizzazione del momento della quantità di moto, perché impone al momento stesso la
condizione di assumere solo valori quantizzati discreti, variabili ma in modo discontinuo. Esso si rifà alla quantizzazione dell'azione:
Azione = mv * 2πr = n *
h
* 2πr = nh
2πr
La quantizzazione postulata per il momento della quantità di moto determina anche la quantizzazione del raggio delle orbite:
v=
e
h
e
h
m 2 e 2r 2
h2
⇒m
⇒
= n2 2
; mvr = n
r=n
2π
2π
mr
4π
mr
mr
da cui:
rn = n 2
h2
4π 2 me 2
Inoltre viene ad essere quantizzata anche l'energia associata ad ogni orbita elettronica:
E=−
e2
e 2 4π 2 me 2
=− * 2 2
2r
2
n h
da cui:
En = −
2π 2 me 4
n2h2
Il primo postulato viene in definitiva a selezionare, tra gli infiniti stati dinamici variabili con continuità che le leggi della meccanica porterebbero a concepire, solo quelli che effettivamente possono essere realizzati. Questi stati possibili, pur selezionati,
non sono più un'infinità continua come per la meccanica classica, ma un'infinità discontinua, quantizzata. Gli stati dinamici
possibili per l'elettrone rotante sono detti stati quantici dell'elettrone. Introducendo i valori numeri nelle equazioni qui sopra si
ottiene:
rn = n2 * 0,529 * 10-8 cm
En =
−
1
* 13,6 eV
n2
Ai vari stati quantici, quindi, corrisponde una successione discreta di livelli energetici, ed ogni valore di energia che non sia
compreso in questa successione, corrisponde ad uno stato non ammesso per l'elettrone, ossia è proibito. L'energia dell'elettrone
corrispondente ad ognuno degli stati quantici in cui esso può trovarsi, è una costante caratteristica del particolare stato quantico
considerato, ossia, fintantoché l'elettrone ruota su un'orbita corrispondente ad un definito stato quantico, la sua energia è costante, cioè l'elettrone, in queste condizioni, non irradia energia sotto forma di onde elettromagnetiche. I diversi stati quantici, corrispondenti a valori costanti dell'energia, sono detti stati stazionari dell'atomo. Un secondo postulato consente l'interpretazione
dello spettro caratteristico dell'idrogeno atomico. Definiti gli stati quantici stazionari dell'atomo in un nuovo postulato si afferma che l'atomo emette o assorbe energia sotto forma di radiazioni elettromagnetiche solo quando si verificano delle transizioni,
cioè dei passaggi tra stati quantici diversi, e quando ciò si verifica, l'energia corrispondente alla differenza tra i livelli propri
degli stati quantici tra i quali avviene la transizione considerata è emessa o assorbita sotto forma di un unico fotone. Lo stato
normale dell'atomo è quello corrispondente alla minima energia: fornendo all'atomo sufficiente quantità di energia, lo si può
eccitare, portandolo dallo stato quantico fondamentale a stati quantici più elevati (stati eccitati). Naturalmente, data la quantizzazione dei livelli energetici, l'atomo può assorbire solo quantità di energia uguali agli intervalli Ef-Ei fra due definiti livelli
permessi e non quantità qualunque. Quando l'atomo, per assorbimento di energia dall'esterno, è portato in un qualunque stato
eccitato, viene a trovarsi in condizioni di instabilità, possedendo un'energia superiore alla minima che gli è possibile, rappresentata dal suo stato fondamentale: allora, come ogni sistema meccanico, si evolve tendendo allo stato più stabile di minima energia, cioè tenderà a riportarsi allo stato fondamentale. È in queste transizioni elettroniche da stati più eccitati a stati meno eccitati, che l'atomo emette le radiazioni elettromagnetiche caratteristiche. Il principio di conservazione impone che l'energia irradiata
sia ∆E = En-En'. Ora, col suo secondo postulato, Bohr fa l'ipotesi che questa energia sia irradiata sotto forma di un unico fotone. La frequenza dell'onda emessa si ottiene tramite la relazione di Einstein:
En-En' = hν
⇒
ν = En-En'
ovvero, considerando il numero d'onde ( essendo
~ = ν ):
ν
c
25
~ = E n − E n′
ν
hc
che rappresenta la legge di Bohr. Essa rappresenta ancora un distacco dalle leggi classiche secondo cui la frequenza della radiazione emessa dovrebbe essere uguale alla frequenza del moto di rotazione dell'elettrone attorno al nucleo. Sostituendo l'espressione dell'energia, si ottiene:
2
4
~ = 2π me
ν
h3c
1 
2π 2 me 4
 1
~=ℜ  1 − 1 
⇒ν
*  2 − 2  ⇒ ponendo ℜH =
H

3
2
h c
n 
n2 
 n′
 n′
Questo risultato permise un'interpretazione dello spettro caratteristico dell'idrogeno: le varie serie spettrali che si osservano nelle regioni dell'ultravioletto, del visibile e dell'infrarosso, corrispondono ad altrettante serie di transizioni dell'elettrone da stati
quantici più elevati ad altri meno elevati. Una riga spettrale, dunque, viene emessa durante una ben definita transizione elettronica tra due determinati stati quantici, così che lo spettro che noi osserviamo è come l'eco macroscopica dell'insieme delle transizioni elettroniche che si verificano contemporaneamente in un gran numero di atomi variamente eccitati. A mano a mano che
n aumenta, va progressivamente diminuendo la differenza dei dislivelli corrispondenti alle transizioni che danno origine a due
righe successive della stessa serie, essendo costante per esse il livello di arrivo. Il limite di convergenza per n→∞ ci dà la misura del dislivello ∆E tra il livello fondamentale En' della serie ed il limite E∞:
En = −
2π 2 me 4
⇒ E∞ = 0
n2h2
Quindi il limite di convergenza fornisce la misura sperimentale di E che rappresenta, cambiato di segno, l'energia che è necessario fornire per allontanare l'elettrone a distanza infinita dal nucleo, sicché il limite di convergenza consente di calcolare l'energia di ionizzazione . Per l'idrogeno, considerando la serie di Lyman (ns=1), si ottiene:
Eion = 13,6 eV
Dividendo l'energia di ionizzazione per la carica dell'elettrone, si ottiene il così detto potenziale di ionizzazione, che definisce
la d.d.p. sotto cui l'elettrone viene estratto dall'atomo, determinandone la ionizzazione.
L'interpretazione degli spettri di raggi X secondo Bohr-Sommerfield
Il meccanismo di emissione dei raggi X caratteristici si può descrivere nei termini seguenti. Gli elettroni emessi dal catodo del
tubo Röntgen vengono accelerati dalla d.d.p. applicata al tubo stesso, colpiscono gli atomi dell'anticatodo con un'energia cinetica sufficientemente alta da strappare ad essi uno degli elettroni rotanti sulle orbite più interne, proiettandolo fuori dal raggio
d'azione del nucleo. Quando un atomo viene privato di uno dei suoi elettroni più interni, nella sua compagine elettronica viene
a formarsi una lacuna che altri elettroni rotanti su orbite più esterne tenderanno a riempire, passando ad occupare quel posto
libero che la sua espulsione ha reso disponibile e realizzando così uno stato più stabile di minore energia. In queste transizioni
elettroniche da livelli energetici più alti all'uno o all'altro dei livelli più profondi si verifica, conforme alla legge di Bohr, l'emissione di radiazioni elettromagnetiche la cui frequenza ν = ∆E/h è molto alta ( essendo grande la distanza tra i due livelli energetici di partenza e di arrivo ) e corrisponde alla zona spettrale dei raggi X. L'origine delle serie K, L, M,... è allora facilmente interpretabile: un atomo dell'anticatodo emette una radiazione corrispondente ad una riga della serie K se l'elettrone incidente su
di esso ha sufficiente energia da espellere un elettrone dal livello K. Il posto lasciato libero dalla sua eliminazione potrà allora
essere occupato da un elettrone che si muova su orbite di più elevata energia, dello strato L, M, N, ... Se questo è un elettrone
dello strato L, allora verrà emessa la radiazione della serie K designata col simbolo Kα, se è un elettrone dello strato M, la radiazione emessa sarà la Kβ e così via. Dunque anche l'emissione dei raggi X, come l'emissione delle radiazioni caratteristiche
degli spettri ottici, richiede l'eccitazione degli atomi, ma perché siano emessi gli spettri ottici nell'infrarosso, nel visibile e nell'ultravioletto si deve realizzare semplicemente il salto dell'elettrone responsabile, che è un elettrone esterno all'atomo, dal suo
proprio livello ad uno superiore dal quale poi rientrerà, mentre per l'emissione degli spettri X è necessario che sia fatto libero
un posto in uno dei livelli più profondi, così da provocare una transizione elettronica non alla periferia dell'atomo, ma nei suoi
strati elettronici più interni.
Funzionamento dei L.A.S.E.R.
Anche se l'atomo di Bohr non è definitivo, è interessante per molti spunti geniali. Il L.A.S.E.R. ad esempio, è basato sull'assorbimento e l'emissione di elettroni. Supponiamo di avere un gas monoatomico ( o anche molecolare). Fornendo energia ne eccito
gli atomi che passano da E1 a E2. Ma ogni sistema fisico tende a decadere spontaneamente (l'atomo si diseccita ed emette un
fotone). Ciò se non ci sono interventi. Ma se il gas è investito da una radiazione elettromagnetica di frequenza ν = ∆E/h, possono presentarsi due casi:
1) se l'atomo è in E1 il fotone viene assorbito e l'elettrone passa in E2. Il fotone sparisce.
2) se l'atomo è in E2 l'elettrone ritorna in E1 ed emette un fotone di stessa frequenza. In totale si hanno due fotoni di stessa
frequenza.
Il caso 1 e 2 sono equiprobabili (dimostrato da Einstein). Nel secondo caso ho amplificazione da radiazione.
1) Emissione stimolata
26
dN 2
= - W21 * N2
dt
•
• W21 = σ21 * F
dove W21 è la probabilità di transizione dal livello 2 all'1, F è il flusso di fotoni incidenti e σ21 è la sezione d'urto per
emissione stimolata (se è bassa, le particelle tendono a schivarsi ed il processo non avviene).
2) Assorbimento
dN 1
= - W12 * N 1
dt
•
• W12 = σ12 * F
dove W12 è la probabilità di transizione dal livello 1 al 2, F è sempre il flusso di fotoni incidenti e σ12 è la sezione d'urto per assorbimento.
3) Bilancio tra emissione stimolata ed assorbimento
• posto σ12=σ21 ho che
dF( ν ) dN 1 dN 2
= σ21*F*N2 - σ12*F*N1 da cui si ottiene dF=σ*F*(N2-N1) * dz
=
−
dz
dt
dt
dove dF è la variazione del flusso netto di fotoni incidenti lungo l'asse z. dF>0 (= amplificazione) se N2>N1. In
questo caso si dice che si è verificata una inversione di popolazione, cioè il numero di atomi al livello 2 è maggiore
di quelli al livello 1 (situazione opposta a ciò che avviene normalmente). dF<0 se N2<N1 (condizione che si ha
normalmente). Normalmente N2<N1 in quanto N2/N1 = e - (E2-E1)/kt che normalmente è minore di uno. Quindi in
condizione di equilibrio prevale l'assorbimento. Si noti che anche potendo invertire la popolazione si ottiene al
massimo N2=N1 , cioè dF=0.
3
2
Decad. Rapido
1
Decad. Rapido
2
ν2,1 Decad. Lento
ν2,1
Decad. Lento
(Laser)
ν1,0
ν1,0 (Laser)
ν0,2
1
ν0,3
0
Laser a 3 livelli
Decad. Rapido
0
Laser a 4 livelli
Il L.A.S.E.R. a 3 livelli è il minimo per funzionare se non c'è inversione di popolazione. Un fotone con frequenza opportuna fa saltare un
elettrone dal livello 0 al livello 2. Dal qui l'elettrone salterà molto veCavità risonante con mezzo attivo
locemente al livello 1, in quanto questa transizione è molto probabile.
Fascio Il passaggio dal livello 1 al livello 0 è invece più lento, cosicché molti
Laser
elettroni si trovano a livello 1 e pochi sono a livello 0 (inversione di
popolazione). Quando arriva un fotone di frequenza tale da consentire
il passaggio dell'elettrone dal livello 1 al livello 0, verranno emessi due
fotoni di questa frequenza, provocando così una amplificazione. La
distanza tra i due specchi posti all'estremità della cavità risonante deve
Specchio semiriflettente essere un multiplo intero di λ/2, altrimenti si produrranno interferenze
Specchio
distruttive per l'onda elettromagnetica. Questi due specchi fanno sì che
i fotoni che si propagano con direzione non parallela all'asse della cavità vengano espulsi dopo 2 o 3 riflessioni dalla cavità stessa. I fotoni
rimasti hanno grande probabilità di compiere un'emissione stimolata, perché "rimbalzeranno" da uno specchio all'altro restando
molto tempo all'interno della cavità. Quando il fascio raggiunge una certa intensità, parte dei fotoni riusciranno ad uscire dallo
specchio semiriflettente, producendo il tipico raggio L.A.S.E.R. Ci sono diversi tipi di L.A.S.E.R.:
• a gas (Ne, CO2) ;
• allo stato solido (attivati da impurità presenti in alcuni cristalli, per esempio il rubino Al2O3(Cr), con le impurità di cromo
che fanno da mezzo attivo, attuando un L.A.S.E.R. a 3 livelli con λ=6240Å);
• a semiconduttori (come nei lettori di compact disk);
• a eccimeri (molecole eccitate che producono lunghezze d'onda nell'ultravioletto);
• a coloranti;
• a raggi X.
Esistono moltissimi materiali diversi che possono comportarsi da mezzo attivo, ognuno con proprietà diverse. Esistono inoltre
L.A.S.E.R. non continui, chiamati ad impulso che accumulano dentro la cavità risonante molta energia e poi la sparano fuori
tutta in una volta.
27
Lo spin dell'elettrone
Uhlenbeck e Goudsmit formularono nel 1925 l'ipotesi che gli elettroni di un atomo, non solo siano animati da un moto di rivoluzione attorno al nucleo, ma anche da un moto di rotazione attorno al proprio asse. Quindi ogni elettrone, oltre al momento
della quantità di moto p associato al suo moto orbitale, possiede un momento intrinseco di quantità di moto p0 per effetto della
rotazione attorno al suo asse di simmetria. Questo implica anche un momento magnetico µ0 dovuto alla carica dell'elettrone,
momento che è diretto secondo l'asse di rotazione con verso opposto rispetto a p0, per via del segno negativo della carica:
p0 =
1 h = 0,53*10-27 cm2*g*s-1
2 2π
;
µ0 =
e h
= 0,93*10-20 erg*gauss-1
2mc 2π
Il momento magnetico µ0 viene anche detto magnetone di Bohr e rappresenta l'unità usata per esprimere i momenti magnetici
degli atomi, mentre il momento meccanico p0 viene detto spin dell'elettrone. Indicando con z la direzione del campo magnetico
ed ms il valore della proiezione di p0 in tale direzione:
(p0)z = ms *
h
2π
ms viene detto numero quantico di spin e può assumere valori +½ e -½ a seconda del senso di rotazione dell'elettrone.
Principio di esclusione di Pauli
Lo stato di un elettrone in un atomo è completamente determinato dai numeri quantici n, l, ml, ms dove i primi 3 definiscono
l'orbita percorsa dall'elettrone e la sua orientazione nello spazio ed il quarto definisce il verso in cui è orientato il momento di
spin. Tali numeri quantici definiscono la configurazione elettronica degli elettroni. Nello stato fondamentale ogni atomo ha la
configurazione a cui compete la minima energia. Nel 1925 Pauli definì una legge per la distribuzione degli elettroni nei diversi
stati quantici disponibili, detta principio di esclusione: in un atomo non può esistere più di un elettrone in uno stato definito da
una data quaterna di numeri quantici. Esso sancisce che non si possono avere due elettroni con gli stessi valori di n, l, ml, ms.
Ciò significa che su una determinata orbita possono ruotare al più due elettroni con spin antiparalleli ½ e -½ . I vari elettroni
occupano gli stati di energia più bassa che siano disponibili, ruotando attorno al nucleo sulle corrispondenti orbite occupate a
due a due a spin antiparalleli.
n = 1 ⇒ 2 elettroni (strato K)
n = 2 ⇒ 8 elettroni (strato L)
n = 3 ⇒ 18 elettroni (strato M)
28
Meccanica Ondulatoria
Principio di indeterminazione
Il modello atomico di Bohr-Sommerfield era costruito ispirandosi al modello planetario, cioè l'elettrone si muoverebbe attorno
al nucleo seguendo una determinata traiettoria, ovvero percorrendo una determinata orbita ellittica o circolare. Successivamente, però, si trovò che è impossibile definire le traiettorie precise degli elettroni in quanto l'orbita elettronica non è osservabile e
quindi è impossibile tentare di definirla. Dalle leggi della dinamica, conoscendo la forza che agisce su un punto, è possibile ricavare la velocità e lo spostamento mediante successive integrazioni ed eliminando le costanti di integrazione tramite la conoscenza delle condizioni iniziali. Tuttavia, è impossibile determinare contemporaneamente la posizione e la velocità di un elettrone rotante attorno al nucleo di un atomo, in quanto non restano definite le condizioni iniziali, e ciò comporta l'impossibilità
di definire l'orbita percorsa dall'elettrone ed impone, di conseguenza, la rinuncia al modello atomico di Bohr-Sommerfield. Il
principio di indeterminazione formulato da Heisenberg, esprime questa impossibilità di pervenire ad una determinazione simultanea della posizione e della velocità di un elettrone di un atomo.
Quando si analizzano i fenomeni microscopici, le perturbazioni indotte dalla osservazione diventano determinanti e di conseguenza gli elementi essenziali per definire il moto di un elettrone, vale a dire posizione e velocità, in un dato istante, risultano
facilmente indeterminati, perché concettualmente inosservabili con un'approssimazione significativa per la loro definizione.
Questo poi deriva dal fatto che l'energia è quantizzata, cioè non è possibile ridurre la quantità di energia in gioco ad una misura
al di sotto del singolo quanto, il cui ordine di grandezza è fissato dalla costante di Plank. Supponiamo di osservare una sorgente
di luce puntiforme Si con una lente L e sia I l'immagine di S. Se I fosS
Si
se l'immagine di un elettrone fornita da un fascio di fotoni usato per
illuminarlo, allora non si avrebbe la certezza riguardo la posizione dell'elettrone in quanto potrebbe cadere in un qualsiasi punto del cerchio
θ
di centro S. Detto allora θ la semiapertura angolare della lente e λ la
lunghezza d'onda della radiazione usata per illuminare l'elettrone, si ha
L
che l'indeterminazione ∆x della posizione è data da:
∆x ≅
λ
2 sen θ
L'ordine di grandezza dell'indeterminazione ∆x è quello stesso di λ ed
essa non può essere nulla perché qualunque sia il tipo di radiazione
I
per osservare l'elettrone, essa avrà sempre una lunghezza d'onda finita.
Inoltre c'è anche da considerare l'effetto Compton: quando il fascio di
fotoni colpisce una miscela di particelle materiali, essi vengono da
L
queste deviati dal loro cammino, cioè sono diffusi in varie direzioni e
questa diffusione comporta una diminuzione della loro frequenza a
seconda dell'angolo di diffusione. Nell'iterazione con le particelle materiali, i fotoni di una radiazione elettromagnetica si comportano come
se possedessero una quantità di moto mv=h/λ. Anche in questo caso si fotone h/λ
assiste all'indeterminazione della quantità di moto,. cioè della velocità
dell'elettrone, data da:
-h/λsenθ
Y
θ
e
+h/λsenθ
2h
∆(mvx) =
sen θ
λ
Da queste considerazioni si arriva alla conclusione che, fintantoché si vuole misurare solo la posizione o solo la velocità dell'elettrone, è possibile trascurare l'incertezza della misura determinandola così con esattezza, ma se si vogliono misurare contemporaneamente le due grandezze, non si possono realizzare neppure concettualmente condizioni nelle quali risultino simultaneamente trascurabili le indeterminazioni della misura della posizione e della velocità, nel senso che quanto più precisa sarà la
misura della posizione, tanto più indeterminato sarà il valore della velocità e viceversa. I limiti di tale indeterminazione sono:
∆x * ∆vx ≅
h
m
( Ia relazione di indeterminazione di Heisenberg)
Un'altra relazione è data dalla incertezza ∆E della misura dell'energia di una particella e la durata dt della misura stessa.
∆E = mvx * ∆vx ⇒ vx =
∆x
∆t
,
∆vx =
h
m∆x
∆E * ∆t ≅ h
(IIa relazione di indeterminazione di Heisenberg)
Quindi, sulla base del principio di indeterminazione, piuttosto che di posizioni successivamente occupate da ogni elettrone, si
dovrà parlare di probabilità che l'elettrone considerato si possa trovare in uno o in un altro punto.
29
Onde di de Broglie e la meccanica ondulatoria
L'ottica geometrica descrive fenomeni nei quali il moto degli elettroni è descrivibile mediante le leggi classiche della meccanica
del punto. L'ottica ondulatoria descrive quei fenomeni ai quali non sono applicabili le leggi classiche. Quindi possiamo dire che
i raggi luminosi nella loro propagazione sono guidati dall'indice di rifrazione del mezzo in cui si propagano così come i raggi
elettronici sono guidati dal potenziale. Quando un raggio luminoso è fatto passare attraverso un'apertura molto ristretta, si presenta il fenomeno della diffrazione della luce, cioè dello sparpagliamento dei raggi al di là della stretta apertura attraversata,
determinando su uno schermo che li raccolga, una serie di anelli luminosi. Tale fenomeno viene interpretato con le leggi dell'ottica ondulatoria considerando la luce come manifestazione di un fenomeno ondulatorio, cioè come onde elettromagnetiche. De
Broglie ipotizzò che i fenomeni di diffrazione si rendono manifesti non solo con le radiazioni luminose, ma anche con i raggi
elettronici indirizzati su monocristalli o su sottili fogli metallici policristallini. I cristalli, con la loro struttura reticolare, fungono da reticoli di diffrazione ideali per le radiazioni di lunghezza d'onda molto piccola come i raggi X o i raggi elettronici. Da
questo studio si arrivò alla conclusione che alla propagazione dei raggi elettronici si accompagna un fenomeno ondulatorio,
come accade per la propagazione dei raggi luminosi, cioè la propagazione di un fascio di elettroni comporta la propagazione di
un sistema di onde dette onde di de Broglie, come la propagazione di un fascio di fotoni comporta la propagazione di un sistema di onde elettromagnetiche. Più avanti questa intuizione fu estesa a tutte le particelle materiali di dimensioni atomiche o subatomiche. Le onde di de Broglie, di natura completamente diversa dalle onde elettromagnetiche, sono definite da:
λ=
h
mv
In particolare, se si considera un fascio di elettroni accelerati da una d.d.p. V, si avrà che:
1
mv 2 = eV ⇒ λ =
2
h
; E = E pot + E cin ⇒ λ =
2meV
(
h
2m E − E pot
)
Dalla definizione, si deduce che le onde di de Broglie hanno lunghezza d'onda più piccola quanto più grande è la velocità e la
massa delle particelle. Quando si vuole descrivere il moto di un elettrone entro un atomo, non si può ricorrere alle leggi della
meccanica classica, perché la sua traiettoria è caratterizzata da un raggio di curvatura di 10-8cm, cioè dell'ordine di grandezza
della lunghezza d'onda delle onde di de Broglie. Quindi, per descrivere tale moto si dovrà utilizzare la meccanica ondulatoria.
Equazione di Schrödinger
Consideriamo un fascio di fotoni: per quanto visto nell'effetto fotoelettrico, la sua intensità è
direttamente proporzionale al numero di fotoni e la costante è E=hν. Per cui si avrà I = Nfotoni *
E. Suppongo di avere un'intensità così debole che il fascio si riduca ad un unico fotone: I = E =
hν. Per l'elettromagnetismo classico, il fotone dovrebbe finire in P, contrariamente all'andamento in figura: se faccio passare un fotone per volta, però, conducendo l'esperimento a lungo ottengo lo schema in figura.
Probabilità =
Ip
n fotoni * E
* ds * dt
La meccanica ondulatoria si sviluppa sulla base di un'equazione fondamentale, nota come equazione di Schrödinger, che nella
meccanica atomica prende il posto occupato nella meccanica classica macroscopica dalla legge della dinamica F = ma. L'equazione di Schrödinger è un'equazione differenziale che ha la tipica forma dell'equazione che descrive la propagazione di un'onda
(equazione delle onde):
1 ∂ 2f
∂ 2f ∂ 2f ∂ 2f
+
+
=
∂x 2 ∂ y 2 ∂z 2 v 2 ∂ t 2
dove v è la velocità di propagazione delle onde considerate ed f è una funzione dello spazio e del tempo il cui significato è diverso secondo il tipo di onde che si considera: per esempio nel caso di un'onda elettromagnetica corrispondente ad una radiazione luminosa, f può essere una qualunque componente del campo elettrico o del campo magnetico dell'onda medesima. Riferendoci alle onde elettromagnetiche (date le significative analogie tra fasci di fotoni e fasci di particelle materiali), possiamo
comprendere la forma specifica dell'equazione. La soluzione dell'equazione precedente per le onde elettromagnetiche definisce
le componenti del campo elettrico e magnetico. Note queste componenti, si può calcolare, come funzione quadratica delle stesse, la densità di energia elettromagnetica in ogni punto dello spazio o l'intensità di illuminazione su una qualunque superficie
investita dal fascio di onde considerato: l'una e l'altra sono legate da probabilità dei fotoni di trovarsi in un certo istante entro un
elemento di volume dV o su un elemento ds della superficie illuminata. L'ottica ondulatoria consente così di definire una probabilità di distribuzione dei fotoni entro una certa zona dello spazio. Analogamente, la meccanica ondulatoria ci fornisce una
descrizione probabilistica della distribuzione delle particelle materiali considerate, ossia ci permette di definire la probabilità di
presenza degli elettroni di un atomo nei vari punti dello spazio. Analogamente l'equazione fondamentale della meccanica ondulatoria non fornisce direttamente la probabilità ℘(x,y,z,t) di distribuzione degli elettroni, ma definisce una funzione ψ(x,y,z,t)
detta funzione d'onda, dove ψ2 ha il significato di densità di probabilità ℘(x,y,z,t) dato che, essendo dV un generico ele-
30
mento di volume, la probabilità di trovare l'elettrone nell'intorno del punto (x,y,z) è data da ψ2dV. Perciò la funzione d'onda
ψ deve soddisfare la condizione di normalizzazione:
∫V∞ ψ2 dV = 1
dove l'integrale si intende esteso a tutto lo spazio V∞: infatti detto integrale rappresenta la probabilità che la particella si trovi,
in un determinato istante, in un punto qualunque dello spazio a sua disposizione, e questa probabilità equivale ovviamente alla
certezza. L'equazione diviene:
∂ 2 ψ ∂ 2ψ ∂ 2 ψ 1 ∂ 2 ψ
+
+
=
∂ x 2 ∂ y 2 ∂ z 2 v 2 ∂t 2
da cui, essendo v = λν e ricordando che per de Broglie vale:
λ=
(
h
2m E − E pot
)
otteniamo:
∂ 2ψ ∂ 2ψ ∂ 2ψ
∂ 2ψ
2m
+
+
=
−
*
E
E
*
pot
∂ x 2 ∂y 2 ∂ z 2 h 2 ν 2
∂t 2
(
)
Esprimendo la ψ come funzione sinusoidale del tempo (il che equivale a considerare onde di de Broglie "monocromatiche"), si
può derivare la forma usuale della equazione di Schrödinger per gli stati stazionari, cioè per gli stati di energia costante e
quindi indipendenti dal tempo:
∂ 2 ψ ∂ 2 ψ ∂ 2 ψ 8π 2 m
+
+
+
* E − Epot * ψ = 0
∂ x 2 ∂ y 2 ∂z 2
h2
(
)
Introducendo l'operatore di Laplace:
∇2ψ =
∂ 2 ψ ∂ 2ψ ∂ 2 ψ
+
+
∂ x 2 ∂ y 2 ∂z 2
l'equazione diventa:
∇ 2ψ +
8π 2 m
* E − E pot * ψ = 0
h2
(
)
L'atomo di idrogeno nella descrizione della meccanica ondulatoria
Applicando all'elettrone in moto attorno al nucleo l'equazione di Schrödinger, ponendo Epot=-e2/r:
e2 
∂ 2 ψ ∂ 2 ψ ∂ 2 ψ 8π 2 m 
*E − * ψ = 0
+ 2 + 2 +
2
2
h
r 
∂x
∂y
∂z

la sua integrazione porta a rilevare i seguenti fatti essenziali:
1) Essa ammette soluzioni accettabili, cioè consente di definire delle funzioni d'onda ψ appropriate, solo per valori determinati
dell'energia E (detti autovalori), definiti dall'espressione E n = −
2π 2me 4
. Il numero n è il numero quantico principale deln2 h2
la teoria di Bohr-Sommerfield. La quantizzazione dell'energia dell'elettrone, cioè l'esistenza di livelli energetici discreti, non
deriva da postulati arbitrariamente imposti, ma è una conseguenza logica della natura di quella equazione e delle condizioni
a cui deve soddisfare la ψ per avere significato fisico.
2) Le funzioni d'onda ψ che per i valori sopra specificati dell'energia sono soluzioni dell'equazione di Schrödinger (dette autofunzioni), sono funzioni complicate delle coordinate dello spazio che contengono tre numeri quantici. I numeri quantici che
definiscono le singole autofunzioni sono:
• Numero quantico principale n (n = 1,2,...): definisce l'energia dell'elettrone tramite la relazione E n = −
2π 2me 4
n2 h2
• Numero quantico azimutale l (l = 0,...,n-1): definisce il momento della quantità di moto orbitale dell'elettrone tra*
mite la relazione p =
l(l + 1) *
h
2π
• Numero quantico magnetico ml (ml = -l,...,0,...,l): definisce la proiezione del momento stesso sulla direzione z di
un campo magnetico esterno, tramite la relazione p z = m l
h
2π
Ogni autofunzione associata ad una definita terna di numeri quantici n, l, ml (ψn,l,ml) è chiamata orbitale. Ogni orbitale corrisponde ad un determinato stato quantico per l'elettrone. Gli orbitali corrispondenti al numero quantico secondario l=0 sono detti
orbitali S, quelli corrispondenti al numero quantico l=1 sono detti orbitali P e così via. La tabella seguente mostra le denominazioni degli orbitali ed il loro numero totale in base al valore dei primi tre numeri quantici:
n
l
ml
Tipi di orbitali
Numero di Orbitali
1
0
0
1s
1
31
2
0
0
2s
1
2
1
0,±1
2p
3
3
0
0
3s
1
3
1
0,±1
3p
3
3
2
0,±1,±2
3d
5
4
0
0
4s
1
4
1
0,±1
4p
3
4
2
0,±1,±2
4d
5
4
3
0,±1,±2,±3
4f
7
Ai diversi orbitali corrispondono ben determinati valori dell'energia dell'elettrone: per l'atomo di idrogeno, con un solo elettrone, essi dipendono dal solo numero quantico principale n. Gli orbitali caratterizzati dallo stesso livello energetico sono detti
degeneri. Il concetto di orbitale sostituisce nella meccanica ondulatoria quello intuitivo di orbita del modello classico di BohrSommerfield. Un orbitale è ancora definito da un'equazione matematica, anche se complessa, ed è visualizzabile riferendosi a
ψ2 che determina punto per punto l'ampiezza della probabilità che l'elettrone si trovi nell'intorno del punto considerato. Si
può dare un'utile rappresentazione tracciando le superfici di uguale probabilità (ψ2=cost.) ed assumendo quella che rappresenta il 95% di probabilità di trovarvi l'elettrone attorno al nucleo ∫V ψ2dV = 0,95. Il moto dell'elettrone dunque, che non è
descrivibile da alcuna definita traiettoria, determina una distribuzione di carica assimilabile ad una sorta di nuvola diffusa per
tutta l'estensione dell'orbitale che corrisponde al suo proprio stato quantico e caratterizzata da densità diversa da punto a punto.
Orbitali s
Consideriamo i contorni per le superfici 1s e 2s: la probabilità di trovare
l'elettrone nei vari punti dello spazio attorno al nucleo dipende solo dalla
distanza da esso. Perciò si dice che gli orbitali s hanno simmetria sferica.
Consideriamo ora la rappresentazione della nuvola di carica. Il numero di
punti per unità di volume (punti-immagine) è proporzionale a ψ2. La
probabilità che un elettrone si trovi a distanza r dal nucleo si può calcolare come la probabilità che esso si trovi entro uno strato sferico di raggio r e spessore infinitesimo dr, perciò risulta p = ψ2 4 π r2 dr. Chiamiamo p funzione di distribuzione della probabilità, cioè la probabilità
di trovare l'elettrone a quella distanza dal nucleo.
Orbitali p
A differenza degli orbitali s che sono a simmetria sferica, gli orbitali p hanno simmetria assiale essendo rappresentati da una superficie a due
lobi tangenti l'uno all'altro in corrispondenza del
nucleo e separati da un piano nodale sul quale
ψ2= 0.
32
Orbitali d
Le superfici limiti di questi orbitali, se si
eccettua l'orbitale dZ2, sono tutti a 4 lobi
che si espandono in direzioni diverse per i
diversi orbitali.
Le funzioni d'onda degli orbitali atomici
È utile fare un cenno sulla forma matematica delle funzioni d'onda che definiscono i singoli orbitali. Si fa di solito riferimento
al sistema di coordinate polari ρ, θ, ϕ. La funzione d'onda può, con tale scelta, essere espressa nella forma:
ψ = ℜnl(ρ) ∗ Θln(θ) ∗ Φn(ϕ)
dove ℜnl(ρ) rappresenta la parte radiale della funzione, mentre Θln(θ) e Φn(ϕ) ne rappresentano la parte angolare. Detto a0 il
primo raggio dell'orbita di Bohr, cioè a0= h2 / 4π2me2, abbiamo per gli orbitali s:
ψ(2s) =
−
1
ψ(1s) =
πa 0
e
r
1
4 2πa 0
3
r
a0
3

r  − a0
2
e
−

a 0 

e per gli orbitali p:


1
2
ψ2px =  3  sen θ cos ϕ ℜ (ρ )
 
 4π 



1


2
ψ2px =  3  sen θ sen ϕ ℜ(ρ )


 4π 



1


2
ψ2px =  3  cos θℜ (ρ )


 4π 



dove abbiamo:
3
r
−
1  1 2 r
a0
ℜ(ρ) =

 * *e
3  2a 0  a 0
Gli atomi con più elettroni nella descrizione della meccanica ondulatoria
La differenza fondamentale nella trattazione degli atomi con più elettroni nasce dal fatto che l'espressione dell'energia potenziale da introdurre nella equazione di Schrödinger per la determinazione dei vari livelli energetici e dei vari orbitali che definiscono i diversi stati quantici propri degli elettroni presenti, oltre ai termini che descrivono l'attrazione coulombiana di ogni elettrone da parte del nucleo, contiene anche termini corrispondenti alle mutue repulsioni fra gli elettroni, il che rende praticamente
insolubile l'equazione stessa. Ci si può rendere conto di questa difficoltà riferendosi al caso dell'atomo di elio, il quale possiede
due elettroni rotanti attorno al nucleo. L'energia potenziale sarà espressa dall'espressione:
33
E pot = −
2e 2 2e 2 e 2
−
+
r1
r2
r12
dove con r1 si intende la distanza dell'elettrone 1 dal nucleo, con r2 la distanza dell'elettrone 2 dal nucleo e con r12 la distanza
dell'elettrone 1 dall'elettrone 2 (forza repulsiva). Da questa espressione si ottiene una equazione di Schrödinger come la seguente:
2e 2 2e 2 e 2 
∂ 2 ψ ∂ 2 ψ ∂ 2 ψ ∂ 2 ψ ∂ 2 ψ ∂ 2 ψ 8π 2 m 
*
E
+
+
+
+
+
+
+
+
− * ψ = 0

h2
r1
r2
r12 
∂ x 1 2 ∂y 1 2 ∂ z 1 2 ∂x 2 2 ∂y 2 2 ∂ z 2 2

Se non si tenesse conto dell'ultimo termine dell'energia potenziale, l'equazione sarebbe suscettibile alla facile sostituzione
ψ=ψ1∗ψ2 ottenendo due equazioni semplici della forma propria di un sistema idrogenoide, di cui la prima relativa ad e1 e la seconda ad e2. In questa grossolana approssimazione l'energia complessiva dell'atomo di elio sarebbe data da E=E1+E2. Un'approssimazione migliore (metodo di Hartree) consiste nel considerare ogni singolo elettrone soggetto ad un campo di forze centrali a simmetria sferica, determinato dal nucleo e dall'effetto medio di tutti gli altri elettroni che fanno da schermo tra il nucleo
stesso e l'elettrone considerato, riducendo così l'effetto attrattivo della carica nucleare. L'effetto schermante avvolgente il nucleo
riduce la carica reale Ze ad un valore efficace, detto carica nucleare efficace Zeff, più piccolo. In questa approssimazione è possibile scindere l'equazione globale in tante equazioni monoelettroniche distinte quanti sono gli elettroni dell'elemento, ciascuna
del tipo:
(
)
∂ 2 ψ ∂ 2 ψ ∂ 2 ψ 8π 2 m
* E i − E pot ( i ) ψ i = 0
2 +
2 +
2 +
h2
∂x i
∂y i
∂z i
dove ψi è l'orbitale proprio dell'elettrone i, Ei è la sua energia ed Epot(i) è un termine di energia potenziale anch'esso dipendente
solo dalle coordinate dell'elettrone. Le curve di colore rosso mostrano la distribuzione elettronica negli ioni Li+, Na+, K+, mentre le curve di colore verde sono
relative agli orbitali 2s, 3s e 4s che corrispondono nei 3 casi all’elettrone più
esterno (elettrone di valenza). Le curve mettono in evidenza che questo elettrone ruota normalmente attorno al nucleo a notevole distanza da esso. L'elettrone
di valenza nel suo moto può penetrare anche attraverso la nuvola degli elettroni
interni (come si vede dalle curve), ma la probabilità che questo accada è piccola
rispetto alla probabilità che esso si trovi alla periferia dell'atomo. Una conseguenza fondamentale delle interazioni interelettroniche negli atomi con più elettroni è che l'energia dei vari stati quantici dipende non solo dal numero quantico
principale n, ma anche da quello azimutale l cosicché ad ogni valore di n, agli
orbitali s, p, d non corrisponde più la stessa energia come per l'idrogeno. Il valore dell'energia dei successivi livelli varia col variare del numero atomico: si
osservi, per esempio, che per il potassio (Z=19) agli orbitali 3p segue 4s e non 3d. Col crescere di n, le inversioni si moltiplicano. Infine è opportuno rilevare che soltanto in assenza di campi magnetici esterni, l'energia di un orbitale dipende dai soli
numeri quantici n ed l (in un atomo con più elettroni). Così in tali condizioni solo gli orbitali s non sono degeneri, mentre gli
orbitali p sono tre volte degeneri, i d sono 5 volte degeneri, gli f lo sono 7 volte e così via. In presenza di un campo magnetico,
invece, la degenerazione scompare perché l'energia di ogni orbitale viene ad essere determinata anche dal numero quantico ml.
Anzi, in presenza di un campo esterno è da considerare anche l'ulteriore scissione in due sottolivelli distinti per ogni orbitale,
corrispondente ai due stati di spin possibile per ogni elettrone.
Principio di Pauli e regola di Hund
Il principio di esclusione di Pauli afferma che un orbitale può accogliere al più due elettroni a spin antiparalleli. La regola di
Hund afferma che entro un gruppo di orbitali aventi gli stessi valori di n ed l, e quindi la stessa energia in assenza di campi esterni, gli elettroni tendono preferenzialmente a distribuirsi in orbitali diversi occupandone il maggior numero, piuttosto che
raggrupparsi a due a due a spin antiparalleli, finché ci sia in quel gruppo un orbitale vacante. Inoltre quando più elettroni si distribuiscono isolatamente in orbitali diversi, i loro spin sono paralleli, perché questa è una configurazione energeticamente favorita. In generale, salvo le inversioni, si ha:
1s < 2s < 2p < 3s < 3p < 4s < 3d < 4d < 5s < 4d < 5p < 6s < 4f < 5d < 6p < 7s < 5f < 6d < 7d
La struttura degli atomi nello stato fondamentale
Idrogeno
1s1
• H
1s2
• He Elio
Con l'elio si completa lo strato n=1 (strato k). Configurazione elettronica di grande stabilità che tende a conservarsi inalterata: è
per questo motivo che l'elio appare essere un elemento caratterizzato da una notevole inerzia chimica (gas nobile).
•
•
•
34
Li
Be
B
Litio
Berillio
Boro
[He] 2s1
[He] 2s2
[He] 2s2 2p1
•
•
•
•
•
C
N
O
F
Ne
Carbonio
Azoto
Ossigeno
Fluoro
Neon
[He] 2s2 2p2
[He] 2s2 2p3
[He] 2s2 2p4
[He] 2s2 2p5
[He] 2s2 2p6
Agli orbitali energetici 2s e 2p seguono, a livelli energetici notevolmente più alti, gli orbitali 3s e 3p a cui corrispondono energie di poco diverse.
•
•
•
•
•
•
•
•
Na
Mg
Al
Si
P
S
Cl
Ar
Sodio
Magnesio
Alluminio
Silicio
Fosforo
Zolfo
Cloro
Argo
[Ne] 3s1
[Ne] 3s2
[Ne] 3s2 3p1
[Ne] 3s2 3p2
[Ne] 3s2 3p3
[Ne] 3s2 3p4
[Ne] 3s2 3p5
[Ne] 3s2 3p6
Per gli elementi di numero atomico successivo all'argo, gli orbitali energeticamente più favorevoli ad accogliere i nuovi elettroni costituiscono l'insieme 4s, 3d, 4p. Per il potassio ed il calcio (Z=19 e Z=20) il livello 4s è leggermente più basso, mentre
dallo scandio (Z=21) il livello 3d scende al di sotto del 4s.
•
•
•
•
•
•
•
•
•
•
•
•
K
Ca
Sc
Ti
V
Cr
Mn
Fe
Co
Ni
Cu
Zn
Potassio
Calcio
Scandio
Titanio
Vanadio
Cromo
Manganese
Ferro
Cobalto
Nichel
Rame
Zinco
[Ar] 4s1
[Ar] 4s2
[Ar] 3d1 4s2
[Ar] 3d2 4s2
[Ar] 3d3 4s2
[Ar] 3d4 4s2
[Ar] 3d5 4s2
[Ar] 3d6 4s2
[Ar] 3d7 4s2
[Ar] 3d8 4s2
[Ar] 3d9 4s2
[Ar] 3d10 4s2
Per essendosi già iniziato col potassio il riempimento degli orbitali del gruppo n=4, gli elementi dallo scandio allo zinco corrispondono al riempimento degli orbitali 3d ed anche alla cosiddetta prima serie di transizione.
•
•
•
•
•
•
Ga
Ge
As
Se
Br
Kr
Gallio
Germanio
Arsenio
Selenio
Bromo
Kripton
[Ar] 3d10 4s2 4p1
[Ar] 3d10 4s2 4p2
[Ar] 3d10 4s2 4p3
[Ar] 3d10 4s2 4p4
[Ar] 3d10 4s2 4p5
[Ar] 3d10 4s2 4p6
Il kripton, elettronicamente molto stabile, è il quarto membro della famiglia dei gas nobili. Dopo il kripton, nella serie di elementi dal rubidio (Z=37) allo xeno (Z=54) si realizzano strutture elettroniche parallele a quelle viste dal potassio al cripto, con
la progressiva saturazione degli orbitali 5s, 4d e 5p.
•
•
•
•
•
•
•
•
•
•
•
•
Rb
Sr
Y
Zr
Nb
Mo
Tc
Ru
Rh
Pd
Ag
Cd
Rubidio
[Kr] 5s1
Stronzio
[Kr] 5s2
Ittio
[Kr] 4d1 5s2
Zirconio
[Kr] 4d2 5s2
Niobio
[Kr] 4d3 5s2
Molibdeno [Kr] 4d4 5s2
Tecnezio
[Kr] 4d5 5s2
Rutenio
[Kr] 4d6 5s2
Rodio
[Kr] 4d7 5s2
Palladio
[Kr] 4d8 5s2
Argento
[Kr] 4d9 5s2
Cadmio
[Kr] 4d10 5s2
Gli elementi che vanno dall’Ittio al cadmio, costituiscono la seconda serie di transizione.
•
•
•
•
•
•
In
Sn
Sb
Te
I
Xe
Indio
Stanio
Antimonio
Tellurio
Iodio
Xeno
[Kr] 4d10 5s2 5p1
[Kr] 4d10 5s2 5p2
[Kr] 4d10 5s2 5p3
[Kr] 4d10 5s2 5p4
[Kr] 4d10 5s2 5p5
[Kr] 4d10 5s2 5p6
Lo Xeno è il quinto elemento della famiglio dei gas nobili. Saturati con lo xeno gli orbitali 4d, 5s e 5p, segue a più alta energia
un raggruppamento più complesso: 4f, 5d, 6s e 6p.
•
•
Cs
Ba
Cesio
Bario
[Xe] 6s1
[Xe] 6s2
Segue il lantanio che è il primo dei 10 elementi che formano la serie 5d. Subito dopo il lantanio, gli elettroni, anziché continuare a distribuirsi nel 5d, si distribuiscono negli orbitali 4f. Questa serie è chiamata serie interna di transizione 4f e si sviluppa
dal cerio (Z=58) al lutezio (Z=71). Detti elementi sono chiamati lantanoidi (o lantanidi) perché sono molto simili, come comportamento chimico, al lantanio.
35
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
La
Ce
Pr
Nd
Pm
Sm
Eu
Gd
Tb
Dy
Ho
Er
Tm
Yb
Lu
Hf
Ta
W
Re
Os
Ir
Pt
Au
Hg
Tl
Pb
Bi
Po
At
Rn
Lantanio
[Xe] 5d1 6s2
Cerio
[Xe] 4f2 5d0 6s2
Praseodimio
[Xe] 4f3 5d0 6s2
Neodimio
[Xe] 4f4 5d0 6s2
Promezio
[Xe] 4f5 5d0 6s2
Samario
[Xe] 4f6 5d0 6s2
Europio
[Xe] 4f7 5d0 6s2
Gadolinio
[Xe] 4f8 5d0 6s2
Terbio
[Xe] 4f9 5d0 6s2
Disprosio
[Xe] 4f10 5d0 6s2
Olmio
[Xe] 4f11 5d0 6s2
Erbio
[Xe] 4f12 5d0 6s2
Tulio
[Xe] 4f13 5d0 6s2
Itterbio
[Xe] 4f14 5d0 6s2
Lutezio
[Xe] 4f14 5d1 6s2
Afnio
[Xe] 4f14 5d2 6s2
Tantalio
[Xe] 4f14 5d3 6s2
14
Tungsteno [Xe] 4f 5d4 6s2
Renio
[Xe] 4f14 5d5 6s2
Osmio
[Xe] 4f14 5d6 6s2
Iridio
[Xe] 4f14 5d7 6s2
Platino
[Xe] 4f14 5d8 6s2
Oro
[Xe] 4f14 5d9 6s2
Mercurio
[Xe] 4f14 5d10 6s2
Tallio
[Xe] 4f14 5d10 6s2 6p1
Piombo
[Xe] 4f14 5d10 6s2 6p2
Bismuto
[Xe] 4f14 5d10 6s2 6p3
Polonio
[Xe] 4f14 5d10 6s2 6p4
Astato
[Xe] 4f14 5d10 6s2 6p5
Radon
[Xe] 4f14 5d10 6s2 6p6
Col radon si completa la saturazione del sesto gruppo, separato dal successivo da un notevole intervallo di energia. Il radon è il
sesto membro della famiglia dei gas nobili. Col francio ed il radio si satura l'orbitale 7s, poi con l'attinio diventa più basso l'orbitale 6d. Gli elementi che seguono l'attinio, in cui assistiamo al riempimento di 5f da torio al laurenzio, sono detti attinoidi.
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
Fr
Ra
Ac
Th
Pa
U
Np
Pu
Am
Cm
Bk
Cf
Es
Fm
Md
No
Lr
Francio
Radio
Attinio
Torio
Protoattinio
Uranio
Nettunio
Plutonio
Americio
Curio
Bechelio
Californio
Einsteinio
Fermio
Mendelevio
Nobelio
Laurenzio
[Rn] 7s1
[Rn] 7s2
[Rn] 6d1 7s2
[Rn] 5f2 6d0 7s2
[Rn] 5f3 6d0 7s2
[Rn] 5f4 6d0 7s2
[Rn] 5f5 6d0 7s2
[Rn] 5f6 6d0 7s2
[Rn] 5f7 6d0 7s2
[Rn] 5f8 6d0 7s2
[Rn] 5f9 6d0 7s2
[Rn] 5f10 6d0 7s2
[Rn] 5f11 6d0 7s2
[Rn] 5f12 6d0 7s2
[Rn] 5f13 6d0 7s2
[Rn] 5f14 6d0 7s2
[Rn] 5f14 6d1 7s2
La classificazione periodica degli elementi
Considerando gli elementi uno di seguito all'altro, in ordine di numero atomico crescente, come abbiamo fatto nelle pagine che
precedono, si osserva che ritornano periodicamente, dopo più o meno lunghi intervalli (prevedibili) gli stessi motivi dominanti
nella loro configurazione elettronica, sicché si può dire che questa è una funzione periodica del numero atomico. La successione degli elementi è come scandita periodicamente dalla realizzazione di strutture elettroniche di particolare stabilità, quelle
proprie dei gas nobili. La progressiva saturazione di ciascuno di questi orbitali che compongono questi raggruppamenti definisce i vari periodi della classificazione degli elementi. I sette periodi sono di diversa lunghezza. Passando da un periodo ai successivi non può sfuggire il ripresentarsi di configurazioni elettroniche strettamente analoghe, che designano i membri delle tipiche famiglie naturali degli elementi:
• I° gruppo ⇒ metalli alcalini: presenza di un elettrone solitario rotante in un orbitale s (elettrone di valenza) che può facilmente essere allontanato.
• II° gruppo ⇒ metalli alcalino-terrosi: presenza di un doppietto elettronico in un orbitale s
• VII° gruppo ⇒ alogeni: mancanza di un solo elettrone al completamento dell'ottetto sp tipico dei gas nobili.
• Gruppo 0 ⇒ gas nobili: notevole stabilità dovuta al completamento dell'ottetto sp.
36
37
Il tipo di rappresentazione riportata permette di individuare quattro classi fondamentali di elementi:
1. Gas nobili: se si eccettua l'elio (1s2) i membri di questa classe hanno i sottogruppi di orbitali s e p completamente saturi
formando un ottetto elettronico molto stabile (ns2 np6).
2. Elementi tipici o rappresentativi: i membri di questa classe corrispondono al progressivo riempimento del gruppo di orbitali
più esterno (cioè aventi configurazione elettronica esterna variabile da ns1 a ns2np5). Il loro comportamento chimico è determinato dalla loro tendenza più o meno spiccata ad acquistare o a perdere un certo numero di elettroni o a metterli in comune con altri atomi.
3. Elementi delle serie normali di transizione: progressivo riempimento degli orbitali dei sottogruppi di tipo (n-1)d. Tutti questi elementi sono di tipo metallico. Spiccata tendenza a dare numerosissimi composti di coordinazione (sali complessi).
4. Elementi delle serie interne di transizione: in essi si realizza il progressivo riempimento degli orbitali interni di tipo (n-2)f.
Grande somiglianza nelle proprietà chimiche e fisiche. La serie 4f è quella dei lantanoidi, mentre la 5f è quella degli attinoidi.
Carica nucleare efficace
Le variazioni del raggio atomico lungo i vari periodi ed all'interno dei vari gruppi della classificazione periodica (vedi sezione
seguente), sono parallele ed in senso opposto a quelle della carica nucleare efficace. Passando da un elemento al successivo, la
nuvola elettronica avvolgente il nucleo si arricchisce di un elettrone e contemporaneamente aumenta di un'unità la carica positiva del nucleo. Però, per il nuovo elettrone aggiunto, la carica nucleare è parzialmente schermata dalla compagine elettronica a
cui esso viene addizionato, cosicché l'elettrone medesimo sente l'attrazione di una carica positiva inferiore a quella reale del
nucleo, diminuita dallo schermo degli elettroni, ossia è soggetto ad una carica nucleare efficace (Zeff*e) più piccola di quella
reale (Z*e). L'azione di schermo di ogni elettrone può essere descritta attraverso un'opportuna costante di schermo: in generale
hanno più accentuata azione schermante gli elettroni degli orbitali interni. La carica nucleare efficace risulta gradualmente crescente lungo ogni periodo e quando si passa da un periodo al successivo si verifica una netta caduta del suo valore.
Dimensioni Atomiche
Si definisce raggio apparente di un atomo la metà della distanza minima di avvicinamento fra due atomi della stessa specie in
una molecola o in un cristallo. Lungo ogni periodo il raggio atomico diminuisce gradualmente con l'aumento del numero atomico ed aumenta iniziando un nuovo periodo. Procedendo lungo un periodo, gli elettroni che si aggiungono vanno ad occupare
orbitali con stessa energia e contemporaneamente cresce la carica nucleare, e questo determina una progressiva contrazione degli orbitali occupati e quindi della nuvola elettronica avvolgente il nucleo e di conseguenza anche il raggio atomico. Passando
ad un periodo successivo, gli elettroni vanno ad occupare livelli energetici più alti e quindi molto più espansi e quindi il raggio
atomico aumenta. Nella serie di transizione le variazioni del raggio atomico non si manifestano con regolarità e le variazioni
del raggio atomico risultano di piccola entità. Si definisce volume atomico di un elemento il volume occupato dal suo grammoatomo allo stato solido, cioè il rapporto tra il suo peso atomico e la sua densità in questo stato. Esso ha lo stesso comportamento del raggio atomico.
Energia di ionizzazione
Si definisce energia di ionizzazione Eion di un atomo la quantità di energia necessaria per allontanare a distanza infinita dal nucleo l'elettrone ad esso meno fortemente legato, cioè quello più esterno, trasformando l'atomo X considerato in ione positivo X+
secondo lo schema:
X+Eion ⇒ X++edove e è l'elettrone espulso. Molto spesso si parla di potenziale di ionizzazione Vion che esprime la d.d.p. necessaria per estrarre da un atomo il suo elettrone più esterno. Esso è definito come:
Vion=
E ion
e
È da notare poi che l'energia è diversa per i successivi stadi di ionizzazione, crescendo dal primo stadio al successivo. Inoltre la
seconda ionizzazione è sempre più alta di quella di prima ionizzazione anche se il secondo elettrone viene estratto dallo stesso
orbitale in cui si trovava il primo espulso, in quanto, una volta allontanato l'elettrone, il livello energetico dell'orbitale in cui si
trovava si abbassa per effetto dell'aumento della carica nucleare efficace che tende a contrarre gli orbitali verso il nucleo, legando più fortemente gli elettroni. Lungo ogni periodo si ha un graduale aumento dell'energia di ionizzazione che però diminuisce passando al successivo periodo. Il valore basso dell'energia di ionizzazione dei metalli alcalini è dovuto al fatto che nei loro
atomi l'unico elettrone di valenza è distribuito in un orbitale s che si espande a notevole distanza dal nucleo, mentre tutti gli altri
elettroni formano un complesso fortemente legato al nucleo stesso. Per questi atomi l'elettrone di valenza risulta poco fortemente legato al nucleo. Il valore elevato dell'energia di ionizzazione dei gas nobili deriva dalla grande stabilità della loro struttura
elettronica. Passando al periodo successivo, l'energia di ionizzazione diminuisce e questo è dovuto al fatto che entro ogni gruppo le dimensioni atomiche aumentano dall'alto verso il basso e l'elettrone più esterno si muove a distanza sempre più grande dal
38
nucleo e con energia corrispondente a livelli sempre più alti. Inoltre, tanto più bassa è l'energia di ionizzazione, tanto più
elettropositivo è il carattere dell'elemento considerato, cioè tanto più facilmente l'atomo neutro si può trasformare in ione
positivo. Lungo i singoli periodi l'elettropositività decresce da sinistra a destra ed entro i singoli gruppi cresce dall'alto verso il
basso.
Affinità elettronica
Si definisce affinità elettronica Ea.el. l'energia liberata quando ad un atomo neutro, supposto isolato ed allo stato fondamentale,
viene addizionato un elettrone:
X+e- ⇒ X-+Ea.el.
e rappresenta l'energia di legame tra l'elettrone aggiunto e l'atomo X (si ha quindi una diminuzione di energia del sistema considerato). Lungo un periodo l'affinità elettronica cresce da sinistra verso destra ad eccezione del Be, Mg, N, P ed i gas nobili. Entro uno stesso gruppo essa decresce dall'alto verso il basso, perché negli atomi di piccole dimensioni l'attrazione dell'elettrone
da parte del nucleo è più forte. Si possono anche avere affinità elettroniche di ordine superiore.
Elettronegatività
Gli elementi che hanno un'elevata affinità elettronica tendono a diventare ioni negativi, e si dicono elettronegativi. L'elettronegatività è indice della tendenza di un atomo di attirare a sé elettroni quando si lega ad altri atomi, quindi l'elettronegatività di un
elemento dipende dal numero e dal tipo di atomo che con esso si lega. L'elettronegatività lungo un periodo cresce da sinistra a
destra ed entro i gruppi decresce dall'alto verso il basso.
Carattere Metallico
Costituiscono la classe dei metalli, gli elementi i cui atomi sono caratterizzati da deboli forze attrattive fra elettroni esterni e
nucleo, tali da conferire agli elettroni stessi una notevole mobilità, cioè una notevole facilità di staccarsi dall'atomo a cui appartengono. Costituiscono la classe dei non metalli gli elementi nei cui atomi le forze attrattive tra elettroni e nucleo sono di più
notevole entità, così da trattenerli ad esso stabilmente e favorire eventualmente anche l'addizione di altri elettroni. Quindi il carattere metallico è tanto più accentuato quanto è più bassa l'energia di ionizzazione e decresce con l'aumentare di questa.
Previsioni sul tipo di legami
I tipi fondamentali di legame con cui atomi di elementi diversi si combinano sono essenzialmente due:
1. legame ionico che si realizza attraverso il trasferimento di uno o più elettroni da un atomo ad un altro con la formazione di
uno ione positivo ed uno negativo che mutuamente si attraggono secondo la legge di Coulomb.
2. legame covalente che consiste nella condivisione di una coppia elettronica fra due atomi.
Due atomi tendono a legarsi tra loro con un legame di tipo ionico se uno di essi ha una bassa energia di ionizzazione e l'altro ha
una notevole affinità elettronica. Se i due atomi non hanno queste caratteristiche, essi formeranno un legame di tipo covalente.
Quindi se due elementi appartengono a gruppi diversi e lontani uno dall'altro sarà favorita la formazione di legami ionici, mentre se appartengono a gruppi vicini, sarò favorita la formazione di legami covalenti.
Altre proprietà
Per i gas nobili e per gli alogeni si riscontra un andamento regolarmente crescente con il peso atomico delle temperature di fusione e di ebollizione. Nel caso dei metalli alcalini esse invece diminuiscono col crescere dei pesi atomici.
39
Il legame chimico e la formazione delle molecole e dei cristalli
Introduzione
Gli atomi degli elementi non si trovano quasi mai allo stato di particelle isolate l'una all'altra. La struttura elettronica dei singoli
atomi determina i tipi di geometria degli aggregati atomici che costituiscono le molecole e i cristalli, e le proprietà di questi sono intimamente influenzate dalla struttura e dal tipo di legami fra atomo ed atomo. Due o più atomi tendono a combinarsi tra
loro per realizzare degli aggregati a cui corrisponde un'energia totale inferiore a quella dell'insieme degli atomi isolati l'uno dall'altro. Ogni sistema meccanico tende infatti allo stato di più bassa energia possibile per esso, che rappresenta il suo stato di
massima stabilità. Quando diversi atomi si combinano, ciò avviene secondo ben determinati rapporti fra i numeri di atomi delle
varie specie e non secondo rapporti qualunque (saturazione delle valenze).
Concetto generale di legame chimico: l'energia di legame
Due o più atomi tendono a legarsi l'uno all'altro quando ciò comporta una diminuzione dell'energia totale. Si dice che tra due
atomi A e B si forma un legame chimico quando essi tendono a formare un aggregato stabile AB. Chiamiamo energia elettronica la somma dell'energia cinetica degli elettroni e dell'interazione coulombiana degli elettroni medesimi fra loro e coi nuclei.
Si definisce energia elettronica di legame fra due atomi A e B la differenza tra l'energia elettronica complessiva dell'aggregato
AB e l'energia elettronica dei due atomi A e B isolati. L'energia elettronica di legame non si può identificare con l'energia di
legame cioè con l'energia necessaria per spezzare il legame: di regola questa è un po' inferiore a quella, in valore assoluto, a
causa dell'energia di vibrazione degli atomi che favorisce la rottura del legame. L'energia di legame fra i due atomi A e B si identifica con l'energia di dissociazione del legame AB. Se i due atomi, avvicinandosi fra loro, danno origine ad una molecola
stabile, l'energia E progressivamente diminuisce mano a mano che la distanza internucleare decresce, cioè via via che l'interazione tra i due atomi diventa più energica e raggiunge il valore minimo per un definito valore della distanza internucleare uguale a r0 (distanza di equilibrio). Questo è un valore medio che vario da istante ad istante in quanto i due nuclei non sono fermi,
ma oscillano intorno alle loro posizioni di equilibrio per effetto della vibrazione termica. La profondità D0 rappresenta l'energia
elettronica di legame.
Il legame ionico
Il legame ionico è un tipo fondamentale di legame che di regola si realizza quando un atomo di un elemento fortemente elettropositivo (caratterizzato da una bassa energia di ionizzazione) si combina con un atomo di un elemento fortemente elettronegativo (caratterizzato da un'elevata affinità elettronica). Tuttavia la maggior parte dei legami è di tipo intermedio fra i due estremi
rappresentati dal legame ionico puro e dal legame covalente puro. I legami tipicamente ionici sono dati dagli alogenuri alcalini
(NaCl, KCl).
Cloruro di sodio
Consideriamo una molecola di cloruro di sodio (NaCl) isolata allo stato gassoso, una molecola biatomica di questo tipo esiste
solo a temperature molto elevate perché in condizioni normali essa è formata da cristalli. Consideriamo allora un atomo di cloro ed uno di sodio aventi rispettivamente configurazioni elettroniche [Ne] 3s2 3p5 e [Ne] 3s1. Perdendo un elettrone, il sodio si
trasforma in ione positivo Na+ con carica +1, isoelettronico con l'atomo di neon e quindi stabile. Il cloro acquistando un elettrone si trasforma in ione negativo Cl- con carica -1, isoelettronico con l'argo e quindi stabile. Avendo i due ioni così formati
cariche opposte, essi si attraggono con una forza esprimibile dalla legge di Coulomb. La tendenza degli atomi di sodio e cloro a
trasformarsi in ioni Na+ e Cl- si rispecchia nel basso valore di energia di ionizzazione del primo (Eion(Na)=5,14 eV) e nell'alto
valore dell'affinità elettronica del secondo (Ea.el.(Cl)=-3,82 eV). Per rimuovere l'elettrone dall'atomo di sodio è necessaria un'energia pari alla sua energia di ionizzazione e per addizionare un elettrone all'atomo di cloro viene liberata una quantità di energia pari alla sua affinità elettronica, quindi il costo netto dell'energia del legame ionico così formato è dato da:
Eion(Na) + Ea.el.(Cl) = 5,14 - 3,82 = 1,32 eV
I due ioni poi si formano a reciproco contatto e quindi essi si attraggono con una energia data da:
E Coul om b = −
e2
= − 6, 05eV
r
dove il segno meno indica che la forza è attrattiva. Il bilancio complessivo della variazione di energia che accompagna la trasformazione dei due atomi di sodio e cloro, isolati allo stato gassoso, in due ioni legati insieme nella molecola biatomica di cloruro di sodio, è data dalla somma di tre distinti processi parziali, cioè:
40
∆E=Eion(Na) + Ea.el.(Cl) + ECoulomb = -4,73 eV
Quindi se un atomo di sodio e un atomo di cloro vengono a reciproco contatto, essi tendono a formare l'aggregato ionico
Na+Cl- che rappresenta uno stato più stabile di energia minore. Inoltre l'energia di legame tra i due ioni altro non è che quella
coulombiana ed essa è anche l'energia necessaria per allontanare i due ioni dalla distanza di equilibrio a distanza infinita. Per
essere più precisi, oltre all'attrazione coulombiana sarebbe necessario considerare anche l'energia di repulsione delle nuvole elettroniche dei due ioni, espressa da Born-Meyer:
Erepuls.=b * e-ar
dove a e b sono due costanti dipendenti dagli ioni. In questo modo l'energia interelettronica totale sarebbe:
E TOT = E Coul om b + E Re p = −
e2
+ be − ar
r
Energia reticolare
Il processo di formazione del cloruro di sodio dai suoi elementi costitutivi implica da una parte sodio metallico e molecole biatomiche di cloro gassoso, dall'altra cristalli di cloruro di sodio secondo lo schema:
Na(s) + ½ Cl2(g) ⇒ Na+Cl-(s)
La variazione di energia durante il processo è data dalla somma delle varie energie in gioco nei singoli processi parziali. Dato
che il cloruro di sodio cristallino è un aggregato di ioni, mentre il sodio metallico è un ammasso di atomi neutri ed il cloro gassoso è un insieme di molecole biatomiche, possiamo concettualmente riferirci alla seguente, ipotetica, sequenza di stadi elementari:
1.
Una mole di sodio metallico, cristallino, è vaporizzata così da ottenere una mole di atomi isolati di sodio allo stato gassoso. Questo processo richiede una spesa di energia uguale al calore di vaporizzazione del sodio: ∆EI = +26,0
Kcal*mol-1
2.
Trasformiamo ora una mole di molecole biatomiche di cloro gassoso in atomi liberi di cloro spendendo un'energia pari
all'energia di dissociazione dei legami Cl-Cl: ∆EII = +28,6 Kcal*mol-1
3.
Trasformiamo una mole di atomi Na in una mole di ioni Na+ con una spesa di energia pari all'energia di ionizzazione
del sodio: ∆EIII = +118 Kcal*mol-1
4.
Trasformiamo una mole di atomi Cl in una mole di ioni Cl- liberando un'energia pari all'affinità elettronica del cloro:
∆EIV = -88,2 Kcal*mol-1
5.
Trasformiamo una mole di sodio metallico e mezza mole di cloro gassoso in una mole di ioni Na+ e in una di ioni Clisolati con un'energia data da: ∆EI+∆EII+∆EIII+∆EIV = +84,4 Kcal*mol-1
È l'insieme delle interazioni elettrostatiche fra gli ioni Na+ e Cl-, che attraendosi si ordinano nella regolare architettura del cristallo, a rendere il bilancio energetico favorevole alla formazione del cloruro di sodio cristallino. L'energia liberata nella formazione del cristallo dagli ioni componenti, che disponendosi con regolarità gli uni accanto agli altri costituiscono il così detto
reticolo cristallino, è designata col nome di energia reticolare: essa, nel cristallo, è l'equivalente dell'energia di legame nella
molecola biatomica Na+Cl-. Il calcolo dell'energia reticolare può essere impostato in modo abbastanza semplice considerando
le interazioni elettrostatiche fra gli ioni insieme ammassati nel cristallo.
Per il calcolo consideriamo i termini di interazione
coulombiana fra un determinato ione della cella elementare (quello che in figura è segnato come *) e
tutti gli altri del reticolo. L'energia di interazione fra
lo ione di riferimento e tutti gli altri è data da un'espressione del tipo:
E M = −6
e 2 12 e 2
8 e2 6 e2
+
−
+
r0
2 r0
3 r0 2 r0
che si può tradurre in una forma assai semplice:
e2
E M = −α
r0
È questa l'espressione della energia di Madelung
che costituisce il termine largamente preponderante
dell'energia reticolare: α è detta costante di Madelung ed è una funzione della struttura del cristallo
considerato. Nella forma più generale l'energia di
Madelung è:
E M = −α
q 1q 2
z z e2
= −α 1 2
r0
r0
dove q1=z1e, q2=z2e sono le cariche degli ioni costituenti il reticolo. Col crescere della carica ionica si
41
osserva un forte aumento dell'energia di interazione di Madelung. Essa, come detto, rappresenta la parte preponderante dell'energia reticolare, ma non tutte: accanto all'interazione coulombiana fra gli ioni p necessario considerare anche la repulsione fra
le loro nuvole elettroniche. Poiché le forze repulsive che agiscono fra queste sono attive solo a brevissima distanza, l'energia
corrispondente si può, con ottima approssimazione, valutare considerando solo i sei ioni che direttamente circondano quello di
riferimento, ossia moltiplicando per 6 l'energia di Born-Meyer (Er=be-ar0):
Er=+6be-ar0
che rappresenta l'energia di repulsione. C'è da considerare, però, un altro contributo: gli ioni Na+ e Cl- hanno la struttura elettronica rispettivamente di un atomo di neon e di un atomo di argo, così che si sovrappone un terzo tipo di interazione, della natura stessa delle interazioni che sussistono fra due atomi di gas nobile quando questo, a bassa temperatura, si condensa allo stato liquido per poi solidificare in cristalli. Le forze di interazione che fra di essi agiscono, attive solo a distanza ravvicinatissima,
sono dette forze di London. L'energia reticolare, dunque, risulta essere la somma dell'energia di Madelung, dell'energia di
repulsione interelettronica e dell'energia di interazione di London:
ERET=EM+ER+EL
Nei composti ionici i singoli atomi tendono ad assumere la carica più alta possibile, compatibilmente coi limiti imposti dall'energia di ionizzazione. La massima carica positiva che un atomo può assumere è uguale al numero dei suoi elettroni di valenza,
mentre la massima carica negativa è uguale al numero degli elettroni mancanti al raggiungimento della configurazione satura
del successivo gas nobile. Inoltre, in un cristallo ionico, uno ione non si accompagna solo con un determinato ione di segno
opposto, ma l'intero cristallo è da considerarsi come una macromolecola formata da un gran numero di ioni positivi e negativi.
Quindi i composti ionici allo stato solido non hanno struttura molecolare e per questo si parlerà di grammo-formula e di pesoformula.
Valenza ionica
Si definisce valenza ionica o elettrovalenza il numero di elettroni che un atomo perde o acquista trasformandosi in ione positivo o negativo. Essa rappresenta la capacità di combinarsi tra gli atomi mediante trasferimento di elettroni e si attua da atomi
elettropositivi ad atomi elettronegativi. L'elettrovalenza dipende strettamente dalla sua struttura elettronica.
Raggi ionici e geometria dei reticoli cristallini ionici
Ogni cristallo ionico è un agglomerato di ioni positivi e negativi rinserrati quanto più è possibile gli uni agli altri, ordinatamente, secondo la geometria del proprio reticolo cristallino. Le posizioni relative dei singoli ioni sono determinate dall'equilibrio
tra le forze attrattive e repulsive in gioco, cioè sono quelle per le quali l'energia complessiva dell'aggregato assume il valore
minimo. Il valore minimo dell'energia dell'insieme si realizza quando gli ioni di carica opposta sono alla minima distanza possibile l'uno dall'altro e quelli aventi carica di uguale segno alla distanza massima. Nell'aggregato che ne risulta, ciascun ione è
circondato da un definito numero di ioni di segno opposto, detto numero di coordinazione dello ione considerato. Il numero di
coordinazione degli ioni componenti il reticolo cristallino dipende in maniera essenziale dalle dimensioni effettive degli ioni
stessi. Quando due ioni di carica opposta si attraggono l'un l'altro, la distanza di equilibrio tra i loro centri è determinata dal reciproco bilanciarsi della forza attrattiva coulombiana e delle forze repulsive derivanti dalla sovrapposizione delle nuvole elettroniche più esterne dei due ioni. I valori dei raggi ionici dei vari ioni, positivi e negativi, si possono dedurre dallo studio delle
strutture dei cristalli ionici mediante i raggi X, attraverso la determinazione delle distanze internucleari nei loro reticoli. Si osserva inoltre che lo ione negativo ha sempre dimensioni maggiori dello ione positivo: ciò discende dalla più elevata carica dello
ione positivo (avente il numero atomico più alto del numero degli elettroni orbitanti attorno ad esso), che contrae l'estensione
degli orbitali. Dai raggi ionici, determinando essi la massima distanza di avvicinamento tra gli ioni nel reticolo cristallino, dipende in misura notevole l'energia reticolare. La struttura del reticolo dipende dagli ioni che lo costituiscono: un fattore determinante è la dimensione dello ione più grande, che normalmente è quello negativo. I modelli coordinativi che nei cristalli ionici
realizzano le strutture più compatte nell'impacchettamento degli ioni sono tre:
1. la coordinazione cubica;
2. la coordinazione ottaedrica;
3. la coordinazione tetraedrica.
Il numero di coordinazione degli ioni è 8 nel primo caso, 6 nel secondo e 4 nel terzo.
←Esempio di coordinazione cubica: cloruro di cesio (CsCl)
n° coordinazione 8
42
Esempio di coordinazione ottaedrica: cloruro di sodio (NaCl) →
n° coordinazione 6
←Esempio di coordinazione tetraedrica: blenda (ZnS)
n° coordinazione 4
L'architettura reticolare energicamente più favorevole, corrispondete al valore massimo delle forze coulombiane attrattive, è
quella in cui ogni catione è circondato dal maggior numero possibile di anioni, a contatto con esso e fra di loro senza compenetrarsi reciprocamente. Quale parametro particolarmente significativo atto a definire la tendenza preferenziale verso l'uno o l'altro tipo di coordinazione si può considerare il rapporto dei raggi ionici degli ioni componenti:
rapporto =
raggio +
raggio −
dove con raggio+ si intende il raggio dello ione più piccolo, cioè quello positivo, mentre con raggio- si intende il raggio dello
ione più grande, cioè quello negativo. In generale vale la seguente regola:
Valore del rapporto r+/rTipo di coordinazione
Numero di coordinazione
> 0,732
Cubica
8
Ottaedrica
6
0,732÷0,414
Tetraedrica
4
0,414÷0,225
Proprietà generali dei composti ionici
1. Capacità di condurre la corrente elettrica allo stato fuso: essendo disciolto il reticolo cristallino, gli ioni sono liberi di muoversi e trasportare la carica.
2. Solubilità in acqua, derivante dalla natura elettrostatica del legame ione-ione e dall'alto valore della costante dielettrica o
permettività del mezzo in cui si trovano immerse le cariche. Oltreché dell'effetto della costante dielettrica sull'entità delle
forze coulombiane interioniche, l'elevato potere solvente dell'acqua riguardo i composti ionici è conseguenza diretta dell'interazione tra i singoli ioni e le molecole d'acqua, dovuta al carattere fortemente polare delle molecole medesime, che per la
loro struttura sono assimilabili a piccoli dipoli elettrici. Questa interazione specifica tra gli ioni in soluzione e le molecole
dipolari del solvente è chiamata solvatazione degli ioni e, nel caso specifico delle soluzioni acquose, idratazione. La solvatazione degli ioni è un processo esotermico che favorisce la dissociazione del cristallo.
3. Stabilità molto elevata: ne sono prova gli alti valori delle temperature di fusione e di ebollizione ed il calore latente di fusione.
4. Fragilità: si fratturano facilmente quando sono sottoposti a sollecitazioni che tendono a deformarli.
Il legame covalente
Consideriamo due atomi di idrogeno che combinandosi formano la molecola biatomica H2. Ad entrambi manca un elettrone per
essere isoelettrico con l'atomo di elio, fortemente stabile in quanto gas nobile. Questa struttura può essere realizzata se i due
atomi mettono ciascuno a disposizione dell'altro il proprio elettrone. I due elettroni appartengono insieme all'uno ed all'altro
ruotando entrambi attorno all'uno ed all'altro, completando ciascuno la propria struttura elettronica e realizzando una configurazione più stabile. La coppia di elettroni condivisa dai due atomi costituisce il legame covalente, legame assai forte.
Consideriamo ora due atomi di cloro
che combinandosi tra loro danno una
molecola biatomica Cl2. A ciascuno
manca un elettrone per completare
l'ottetto tipico dell'argo che raggiungono mettendo in comune l'elettrone
spaiato nell'ultimo orbitale 2p.
43
Analizzando adesso il tipo di orbitale che si forma, riconsideriamo i due atomi di idrogeno: quando essi si avvicinano alla
distanza di legame, i rispettivi orbitali 1s1 non saturi, sovrapponendosi, danno origine ad un orbitale unico più espansa nel quale
i due elettroni possono coesistere accoppiandosi a spin antiparalleli. Questo orbitale risultante dalla sovrapposizione dei due
orbitali atomici costituisce un orbitale di legame che appartiene contemporaneamente ai due atomi, cioè alla molecola H2 e per
questo è anche detto orbitale molecolare. Esso comporta un valore dell'energia nettamente più basso di quello dei due atomi
isolati. Nell'orbitale molecolare la densità della nuvola elettronica ha una distribuzione perfettamente simmetrica rispetto ai due
atomi, essendo la coppia elettronica di legame egualmente ripartita fra gli stessi per la loro identità. Il massimo addensamento
elettronico si trova lungo l'asse internucleare H-H nella zona tra i due nuclei. Consideriamo ora i due atomi di cloro che, combinandosi tra loro, danno origine alla molecola biatomica Cl2. Il legame covalente che si forma Cl-Cl è determinato dalla sovrapposizione dei due orbitali 3pz non saturi che danno origine ad un orbitale molecolare di legame nel quale i due elettroni coesistono a spin antiparalleli.
Con lo stesso meccanismo di legame si possono formare legami covalenti anche con atomi diversi, come ad esempio HCl. In
esso si ha la sovrapposizione dell'orbitale 1s1 non saturo dell'atomo di idrogeno con l'orbitale 3p5 non saturo dell'atomo di cloro
che insieme concorrono alla formazione di un orbitale molecolare di legame. Tuttavia la distribuzione elettronica non è più
simmetrica come per le molecole omonucleari, ma essa risulta maggiormente addensata o polarizzata verso l'atomo più elettronegativo dei due ed intorno ad esso, per la sua energica azione attrattiva sulla coppia condivisa.
44
Legami σ e π
La capacità di combinazione di un atomo è data dalla sua valenza. Si ha un legame semplice quando tra due atomi è condivisa
una sola coppia di elettroni. Ad esempio nel fosgene si forma un legame doppio tra carbonio ed ossigeno ed un legame semplice tra carbonio e cloro:
Consideriamo invece il diossido di carbonio (anidride carbonica) CO2: si hanno due legami doppi:
Analizzando la struttura dei legami semplici con riferimento agli orbitali atomici, che sovrapponendosi concorrono alla loro
formazione, si vede che la nuvola elettronica è distribuita simmetricamente attorno all'asse intermolecolare. In altre parole la
distribuzione propria di questi legami ha simmetria cilindrica rispetto l'asse internucleare ed i legami aventi questa caratteristica
strutturale vengono detti legami σ. Diversa è la situazione che si verifica nei legami multipli. Consideriamo la molecola biatomica N2, formata da un legame triplo tra atomo ed atomo di azoto (:N≡N: ). Ogni atomo di azoto ha gli orbitali p non saturi in
quanto si trovano in uno stato di trivalenza (tre elettroni spaiati). Se Z è la direzione dell'asse internucleare, l'orbitale pZ del
primo si sovrappone al pZ del secondo e l'orbitale di legame che si forma è un orbitale σ:
Gli orbitali pY, invece, si sovrappongono in questo modo:
In analogo modo si ottiene πPx. La nuvola elettronica di questo orbitale non è centrale lungo l'asse internucleare e non è distribuito con simmetria cilindrica attorno ad esso, ma si ripartisce in due regioni con la "forma a banana" situate da parti opposte
rispetto a tale asse. I due orbitali di legame py-py e px-px sono del tutto equivalenti e si differenziano solo per la diversa giacitura nello spazio. La densità elettronica non è ripartita lungo l'asse internucleare, ma è ripartita in due regioni identiche fuori dall'asse e da parti opposte rispetto ad esso. Tali legami vengono detti legami π . Quindi i legami σ derivano da orbitali atomici
che si sovrappongono coassialmente ed i legami π da orbitali atomici che si sovrappongono lateralmente. Nei legami multipli si
ha sempre un legame σ ed uno o più legami π (meno forti dei σ).
45
Struttura degli aggregati poliatomici con legami covalenti: molecole, cristalli
molecolari, cristalli covalenti
Quando due atomi si legano tra loro con legami covalenti, gli aggregati che ne risultano possono essere di vario tipo. Possono
formarsi aggregati poliatomici contenenti un numero ben definito di atomi, che esauriscono tutti completamente la loro capacità
di combinazione condividendo gli uni con gli altri i propri elettroni di valenza (diremo in questo caso che gli atomi si combinano in molecole o ioni poliatomici), oppure aggregati di un numero di atomi indefinito che con lo stesso meccanismo di legame
possono arricchirsi di altri atomi senza alcuna limitazione di numero (diremo in questo caso che gli atomi formano reticoli continui di cristalli covalenti). Per le specie chimiche caratterizzate da struttura molecolare, le molecole componenti sono chiaramente e singolarmente individuabili in qualunque stato di aggregazione: gassoso, liquido o solido. Due specie chimiche a struttura tipicamente molecolare sono, ad esempio, lo iodio (I2) ed il diossido di carbonio (CO2). Cristalli di questo tipo, costituiti
da un insieme regolare di molecole, sono chiamati cristalli molecolari. Siccome le forze intermolecolari sono sempre piuttosto
deboli, i solidi a struttura molecolare sono in genere caratterizzati da punti di fusione e di ebollizione relativamente bassi e
spesso sublimano facilmente, vaporizzando. Quanto ai solidi cristallini con struttura di tipo covalente, non molecolare, gli atomi costituenti, legandosi fra loro, formano non singole molecole, ma un reticolo tridimensionale continuo. Ne sono esempi caratteristici il diamante o il quarzo (SiO2). In questi casi l'intero cristallo può essere considerato come un'unica molecola gigante:
sono caratterizzati da punti di fusione assai alti. Altra loro tipica proprietà è la durezza. Essi sono inoltre praticamente insolubili
nei comuni solventi. In realtà, ci sono anche solidi che hanno struttura intermedia tra quella dei cristalli molecolari e quella dei
cristalli con reticolo continuo tridimensionale: si tratta di specie solide caratterizzate da una struttura cristallina a strati costituita da aggregati di atomi legati fra loro da legami covalenti ed estesi indefinitamente in due dimensioni. Un tipico esempio di
struttura a strati ci è dato dalla grafite: gli atomi di carbonio sono distribuiti in strati paralleli, formati da maglie esagonali regolari, fuse insieme. Entro ogni strato i legami fra gli atomi sono di tipo covalente e tra i singoli strati agiscono forze di interazione più deboli, come le forze di Van Der Waals. Quanto alla particolare forma geometrica delle molecole ed all'architettura reticolare dei cristalli covalenti dei vari tipi illustrati, essa è determinata in ogni caso dal tipo degli orbitali atomici che concorrono
a formare i legami fra atomo ed atomo e dalla loro orientazione nello spazio.
Radicali liberi
Si definiscono radicali liberi le molecole in cui non tutti gli elettroni sono appaiati a spin antiparalleli, ma uno o due di essi risultano spaiati. Essi sono riconoscibili per il loro paramagnetismo, essendo caratterizzati da un momento magnetico permanente
misurabile. I radicali liberi sono molto reattivi e tendono a dimezzarsi, cioè a combinarsi a due a due con legami covalenti condividendo i propri elettroni spaiati. Quantunque per la molecola O2 si possa formulare una molecola conforme alla regola
dell'ottetto, del tipo:
con due coppie elettroniche a spin antiparalleli condivise dai due atomi. Uno schema così semplice non è accettabile, in quanto
l'ossigeno risulta paramagnetico ed il momento magnetico proprio di ogni molecola di O2 corrisponde a due elettroni spaiati.
Quindi l'ossigeno molecolare è da considerare un radicale libero:
Legami covalenti polari
Nelle molecole biatomiche eteronucleari, come abbiamo visto, la distribuzione elettronica risulta dissimmetrica, con più accentuato addensamento verso quello dei due atomi che è più elettronegativo, cioè è polarizzata verso detto atomo. Quando i due
atomi fra loro legati sono diversi o quando, per essendo uguali, non hanno identico il proprio contorno, la coppia elettronica del
legame non si ripartisce tra i due atomi in maniera uguale, perché uno di essi lo attrae più energicamente dell'altro, così che nel
complesso esso risulta portatore di una frazione di carica δ−, mentre il secondo, attorno al quale la nuvola elettronica è impoverita, risulta portatore di una frazione di carica positiva δ+. Per esempio nella molecola H-Cl:
δ+ δ−
H - Cl
o anche:
H - Cl
+ →
I legami covalenti di questo tipo sono detti legami covalenti polari. Il legame risulta non polare quando il baricentro delle cariche positive (portate dai nuclei atomici) coincide col baricentro delle cariche negative degli elettroni, mentre risulta polare
quando i baricentri delle cariche positive e negative coincidono.
46
Una molecola polare ha le caratteristiche di un dipolo elettrico, cioè di un sistema costituito da due
cariche puntiformi uguali e di segno opposto, +q e -q, poste ad una distanza r. Esso è definito dal suo
momento dipolare µ:
µ=q*r
µ=qr
+
Il momento dipolare è una grandezza vettoriale avente direzione data dalla congiungente dei centri
delle cariche e verso che va dalla carica +q alla carica -q. I momenti dipolari risultano dell'ordine di 10-10 Franklin * 10-8 cm
(1Å), unità di misura che viene chiamata Debye: 1 Debye = 10-18 Fr*cm. Considerando molecole poliatomiche, ad ogni legame
polare tra due atomi è associabile un momento dipolare di legame non nullo e ad ogni legame apolare un momento dipolare
uguale a zero. Il momento dipolare complessivo di una molecola può essere valutato eseguendo la somma vettoriale dei momenti dipolari propri dei vari legami che formano la molecola. La relazione tra costante dielettrica e momento dipolare è espressa dalla equazione di Debye:
+q
-q
2
µ 
ε −1 M 4 

= πN α +
*
ε+2 σ 3 
3kΤ 
dove σ è la densità ed α la polarizzabilità. Essa è la base per dedurre i momenti dipolari da misure di costante dielettrica in funzione della temperatura.
Legami covalenti polari ed elettronegatività degli atomi
Si è parlato di elettronegatività di un atomo come sua tendenza ad attrarre a sé gli elettroni partecipanti al legame con un altro
atomo. Così definita è una proprietà relativa: è assai utile, però, precisare questo concetto con un parametro numerico. Sono
nate così le diverse scale di elettronegatività. Indicando con χA l'elettronegatività di A e con χB l'elettronegatività di B, il legame A-B tanto più si discosta dal modello di un legame covalente puro, per assumere caratteristiche sempre più prossime a quelle di un legame ionico, quanto maggiore è la differenza tra χA e χB. Se χB>χA gli elettroni si addensano maggiormente sull'atomo B, determinando su di esso una concentrazione di carica negativa. È perciò utile conoscere i valori da attribuire all'elettronegatività degli atomi, perché ci permette di stabilire il tipo di legame che si forma. Un criterio di applicazione generale è la
scala di Pauling. Il metodo di Pauling fa diretto riferimento all'energia del legame A-B: se questo legame fosse covalente puro,
la sua energia di dissociazione potrebbe essere assunta uguale alla media delle energie di dissociazione dei legami A-A e B-B.
L'energia di legame sarebbe uguale alla somma dei contributi propri degli atomi A e B:
( E A−B ) COV = E A−A +2 E B−B
Invece per un qualunque legame A-B fra atomi diversi si determina una energia maggiore in valore assoluto della media suddetta:
∆=(EA-B)SPER - (EA-B)COV
che può essere considerata una misura del carattere polare del legame. Seguendo questo criterio, Pauling ha introdotto la relazione:
χB − χA = ∆
In realtà, nel calcolo di ∆, il termine (EA-B)COV è valutato non come media aritmetica, bensì come media geometrica:
(E )
A − B COV
=
(E
A−A
) * (E )
B −B
Per ottenere i valori da attribuire ad ogni singolo atomo, si è stabilito di considerare come valore di riferimento l'idrogeno, ponendo χH=2,1. Pauling ha proposto anche una relazione che evidenzi la percentuale di carattere ionico di un legame:
1
2

− ( χ A −χ B ) 
4
τ = 1001 − e



Legame covalente di coordinazione ( legame dativo )
Due atomi che si legano l'un l'altro con un legame covalente mettono in comune una coppia elettronica alla quale ciascuno contribuisce con un proprio elettrone. È però molto diffuso anche un altro tipo di legame covalente, nel quale entrambi gli elettroni
della coppia condivisa dai due atomi sono messi a disposizione da uno solo di essi: si parla in questo caso di legame covalente
di coordinazione o legame dativo.
Una molecola di ammoniaca NH3 può reagire con uno ione H+ per formare uno ione ammonio NH4+:
NH3 + H+ ⇒ NH4+
L'atomo di azoto nella molecola NH3 ha una coppia elettronica a spin antiparalleli non
condivisa con gli atomi di idrogeno nei legami N-H: essa determina una concentrazione
di carica negativa sull'azoto tale da attrarre uno ione H+. L'atomo di azoto è il donatore degli elettroni del legame e lo ione H+
ne è l'accettore.
47
Stati di valenza degli atomi
Molto spesso le combinazioni tra gli atomi sono da riferire a stati elettronici
eccitati, detti stati di valenza, così che il numero di legami che essi formano
è determinato non dal numero di elettroni spaiati presenti allo stato fondamentale, ma dal numero di elettroni spaiati proprio dello stato di valenza,
che condiziona le loro capacità di coordinazione. Esempio: Be ⇒ 1s2 2s2. La
bivalenza che gli è propria (BeCl2) è da riferire allo stato elettronico eccitato
1s2 2s1 2p1, derivante da quello fondamentale per promozione di un elettrone. Ed anche nel carbonio lo stato di tetravalenza, tipico della moltitudine
innumerevole dei suoi composti, deriva dallo stato fondamentale per promozione dallo stato 1s2 2s2 2p2 allo stato 1s2 2s1 2p3. Vediamo di chiarire
perché un tomo, quando si combina con altri, si porta spontaneamente in
uno stato elettronicamente eccitato che corrisponde ad un livello di energia
più alto di quello proprio dello stato fondamentale. Si può rilevare che un
atomo che si trovi nello stato eccitato di valenza, possedendo più elettroni
spaiati che nello stato fondamentale, può formare un numero di legami
maggiori di quello che deriverebbe dalla configurazione elettronica dello
stato fondamentale. E poiché la formazione di ogni legame è accompagnata
da una diminuzione di energia propria dell'insieme di atomi che si considera, il bilancio energetico globale che accompagna la formazione di una molecola con un numero maggiore di legami può rendere favorito uno stato
eccitato di valenza rispetto allo stato fondamentale.
Numero di ossidazione
Il numero di ossidazione è il parametro che rappresenta, tra i vari atomi, la ripartizione degli elettroni che realizzano i legami.
Esso cresce da +1 a +7 per gli elementi tipici da sinistra verso destra lungo ogni periodo. Il numero massimo di ossidazione
corrisponde al numero d'ordine a cui l'elemento considerato appartiene. Gli elementi caratterizzati da più stati di ossidazione
hanno proprietà chimiche variabili. In un composto ionico formato da ioni monoatomici il numero di ossidazione di ciascuno
ione si identifica con la sua carica (allo ione Mg2+ corrisponde un numero di ossidazione +2). Nel caso di ioni poliatomici, ad
ogni atomo componente deve essere attribuito il proprio numero di ossidazione (n.o.), mentre la carica ionica è assegnabile solo
allo ione nel suo complesso. Quanto agli aggregati atomici a struttura covalente, il n.o. da assegnare a ciascun atomo si identifica con la carica elettrica che l'atomo verrebbe ad assumere in un modello idealizzato a struttura ionica nel quale le coppie elettroniche di legame fossero attribuite così: di ogni coppia condivisa tra due atomi uguali si conviene di assegnare un elettrone ad
un atomo ed uno all'altro, mentre ogni coppia condivisa tra atomi diversi, asimmetricamente distribuita perché maggiormente
attratta verso l'atomo più elettronegativo, si considera come appartenente totalmente a quest'ultimo.
Regole per derivare i n.o.
1.
2.
3.
4.
5.
48
Rappresentando la specie chimica considerata con la formula di struttura, il n.o. di
ogni atomo si può ottenere facendo la somma del numero dei suoi elettroni partecipanti a legami con atomi più elettronegativi o a questi ceduti, preso col segno
positivo, e del numero di coppie elettroniche condivise con atomi meno elettronegativi o di elettroni ceduti da questi ultimi ad esso, preso col segno negativo.
Il n.o. di una specie elementare è 0 (ad esempio H2 ⇒ n.o. = 0)
il n.o. di uno ione monoatomico è uguale alla sua carica.
H ha n.o. = +1 nei composti, mentre negli idruri (LiH, NaH, MgH2) ha n.o. = -1.
Nei composti O ha n.o.= -2, mentre nei perossidi ha n.o.= -1. Da notare inoltre che in F2O l'ossigeno ha n.o. = +2.
In uno ione poliatomico i n.o. devono essere in accordo con la conservazione della carica.
6.
Quando in un composto sono presenti due o più atomi uguali cui siano da attribuire n.o. diversi, si considera il n.o. medio,
quindi il n.o. in generale può essere anche un numero decimale.
Stati di ossidazione degli elementi e classificazione periodica
Il n.o. di un atomo definisce il suo stato di ossidazione: si può rilevare una stretta correlazione tra gli stati di ossidazione degli
elementi e la loro posizione nella tavola periodica. Il n.o. massimo cresce da +1 a +7 procedendo da sinistra a destra lungo ogni
periodo. Entro ciascun gruppo di elementi rappresentativi, gli stati con numeri di ossidazione positivi più bassi vanno stabilizzandosi col crescere del peso atomico. In generale gli elementi caratterizzati da più stati di ossidazione hanno proprietà chimiche variabili anche notevolmente dall'uno all'altro. Per i metalli, negli stati inferiori di ossidazione, si accentua la tendenza a
dare composti ionici formando cationi, cioè più nette si manifestano le caratteristiche metalliche, mentre negli stati di ossidazione superiori prevale molto spesso la tendenza a formare legami covalenti e a costituire anioni, cioè affiorano caratteristiche
non metalliche. Ciò vale sia per i metalli delle famiglie tipiche, sia per quelle delle serie di transizione. Anche per gli elementi
tipicamente non metallici si rilevano non trascurabili differenze da stato a stato di ossidazione. Basti citare la diversa forza dei
loro acidi ossigenati (ossiacidi) che normalmente cresce con l'aumentare del numero di ossidazione.
La teoria dei legami di valenza (Heitler-London)
Consideriamo l’H2 con i due nuclei A e B ed i due elettroni e1 e e2. Finché i due atomi non interagiscono, e1 ruota attorno ad A
ed e2 attorno a B. Se ψΑ(1) e ψΒ(2) sono le funzioni d’onda di e1 nell’atomo A e di e2 nell’atomo B, lo stato del sistema è dato
dall’equazione:
ψI = ψA(1) ∗ ψB(2)
e l’energia E0 è data dalla somma delle energie in gioco, cioè:
E0= 2 EH
Se
i
due
atomi
interagiscono
tra loro, si può cercare di utilizzare ancora una funzione
r12
e2
e1
del tipo precedente da introdurre nell’equazione di Schrödinger con l’energia potenziale. Quest’ultima è la somma dei termini attrattivi e repulsivi:
rA1
rB2
e2
e2
e2
e2
e2
e2
rA2
rB1
−
−
−
+
+
E POT = −
rA1 rB 2 rA 2 rB1 rAB r12
A
B
L’equazione di Schrödinger ci dà ora l’energia totale del sistema formato dai due arAB
tomi interagenti:
E = 2E H + E (ea1,)B + E (ea2), A + E (Ar,)B + E (er1), e 2
che, indicando con Q la somma algebrica delle interazioni coulombiane, diventa:
E = 2EH + Q
L’energia così calcolata corrisponde alla curva in figura e presenta un minimo per rAB≅0,9 Å, in discreto accordo col valore
sperimentale. Il valore dell’energia elettronica è però molto distante dal valore sperimentale, risultando di 0,25 eV invece di
4,72 eV. L’efficienza della funzione d’onda usata sta nel fatto che essa considera l’elettrone e1 appartenente solo ad A e
l’elettrone e2 appartenente solo a B, ma in realtà quando gli atomi sono vicini, gli elettroni possono venire scambiati senza che
la nuova situazione sia distinguibile dalla precedente. È questa l'osservazione alla base della teoria di Heitler-London che porta
alla definizione di una nuova funzione d'onda:
ψ COV = ψ (A1) * ψ (B2 ) + ψ (A2 ) * ψ (B1 )
e dall'equazione di Schrödinger si ottiene:
Q+ J
E = 2E H +
1 + S2
dove J è un effetto quantistico che si ricollega alla possibilità di scambio tra gli elettroni ed è perciò detta energia di scambio.
S, infine, è una quantità che rappresenta l'entità della sovrapposizione dei due orbitali atomici ed è detta integrale di sovrapposizione:
S = ∫ ψ (A1 ) * ψ (B2 ) * dV1
V∞
Un altro miglioramento si ottiene considerando che i due orbitali ψA e ψB non possono più essere considerati identici a quelli
degli atomi isolati, per le reciproche perturbazioni. Allora per l'H2 si può tenere conto del reciproco effetto schermante dei due
elettroni, considerando, in luogo della carica nucleare reale Z=1, una carica efficace Zeff ≠1. In questo modo si ottiene la curva
III del grafico già visto. C'è però la possibilità che i due elettroni si trovino insieme sullo stesso orbitale secondo gli schemi:
( HA(1)(2) )- + HB+
e
HA+ + ( HB(1)(2) )1
Le funzioni d'onda corrispondenti a queste strutture ioniche sono ψΑ ∗ ψΑ2 e ψΒ1 ∗ ψΒ2 e si ottiene:
ψ ION = ψ1A * ψ 2A + ψ1B * ψ 2B
La funzione d'onda più corretta diventa allora:
ψ = ψCOV + λ ψION
49
che viene rappresentata in figura dalla curva IV e con energia minima pari a 4,10 eV.
Alla funzione ψΑ1 ∗ ψΒ2 + ψΑ2 ∗ ψΒ1 corrispondono spin antiparalleli così che essa è una funzione di legame, mentre alla funzione ψΑ1 ∗ ψΒ2 − ψΑ2 ∗ ψΒ1 corrispondono spin paralleli ed è quindi una funzione di antilegame.
Osserviamo la densità di queste due funzioni:
nel caso del legame, la nuvola elettronica è
addensata tra i due nuclei, mentre nel caso dell'antilegame la nuvola è interrotta da un piano
nodale in cui ψ2 = 0 che equivale ad uno
stato repulsivo.
Risonanza fra due strutture di legame
La distribuzione reale degli elettroni fra due atomi deriva dalla compartecipazione di diverse strutture di legame, così come, ad
esempio, nella molecola di idrogeno dove la situazione effettiva del legame è data dalla concorrenza e dalla sovrapposizione di
tre tipi fondamentali di interazione che sono:
↔
↔
H A: H B
HA+: HBHA-: HB+
1
2
2
1
1
2
ψB ψB
ψ A 1ψ A 2
ψA ψB +ψA ψB
Le strutture di legame sono dette forme canoniche limiti o strutture limiti. Le doppie frecce indicano che esse concorrono contemporaneamente al meccanismo di interazione che determina il legame: si esprime questo concetto dicendo che lo stato di legame è determinato dalla risonanza fra le strutture limiti. Il concetto di risonanza è fittizio e dietro non ci sta una realtà fisica
oggettiva: esso dipende solo dal modello usato per descrivere il legame. Questo concetto è già presente nella funzione di Heitler-London che ipotizzano la risonanza tra HA1HB2 e HA2HB1. Consideriamo dei casi più complessi. In
O
generale un legame covalente è descritto come un ibrido di risonanza ionica-covalente tra le strutture
A: B e A-: B- con A più elettronegativo. Si consideri lo ione CO32- tipico dei carbonati con struttura la
C
struttura simile a quella in figura, con il carbonio tetravalente che forma tre legami σ ed uno π, con i tre
legami σ complanari e formanti angoli di 120°. Dato che i legami multipli sono più corti di quelli semO
Oplici, la struttura non dovrebbe risultare simmetrica, come in realtà avviene. Più realisticamente la struttura dello ione CO32- la si deve esprimere in termini di risonanza tra le tre strutture descritte nella figura seguente:
O
OOC
C
C
-
O OO
OO
O
Il doppio legame non può considerarsi localizzato su un certo atomo di ossigeno, ma delocalizzato, nel senso che può realizzarsi con qualsiasi atomo di ossigeno ed anche le due cariche negative non sono localizzate su due determinati atomi di ossigeno,
ma sono portate dallo ione nel suo complesso.
Orbitali ibridi e geometria molecolare
In genere, i legami di una molecola poliatomica non possono essere convenientemente descritti facendo riferimento ad orbitali
atomici puri, cioè ad orbitali s, p o d singolarmente considerati: solo orbitali atomici ibridi, di tipo misto risultanti dall'incrocio
( o appunto ibridazione ) degli orbitali atomici primitivi propri dell'atomo considerato isolato, possono rendere conto della reale geometria molecolare. Un orbitale ibrido è determinato dal contemporaneo concorso di più orbitali atomici puri di tipo diverso, che possono essere tutti quelli disponibili nell'atomo considerato per la formazione di legami o una parte di essi: dal numero e dal tipo di orbitali puri, che insieme contribuiscono alla formazione di un orbitale ibrido, dipende la forma di questo e la
sua orientazione nello spazio. Come regola generale si può dire che solo orbitali atomici corrispondenti a livelli energetici vicini l'uno all'altro possono tra loro ibridarsi, concorrendo insieme a formare orbitali misti adatti alla realizzazione di legami orientati nelle direzioni che la varia geometria molecolare richiede e tali da assicurare per la loro forma, all'atto della formazione
dei legami, la più estesa sovrapposizione con gli orbitali di altri atomi.
Le funzioni d'onda degli orbitali ibridi
Un qualunque orbitale ibrido è analiticamente definito da una funzione d'onda esprimibile come una combinazione lineare delle
funzioni d'onda proprie degli orbitali puri componenti:
50
Ψi = aiψ(s) + biψ(px) + ciψ(py) + diψ(pz)
I coefficienti determinano il grado di mescolamento dei vari orbitali. La migliore combinazione degli orbitali componenti è
quella che minimizza l'energia dell'insieme, ovvero che realizza la massima sovrapposizione. Essi sono determinabili in base
alle condizioni di normalizzazione e di ortogonalità:
• ∫ψi2 dV = 1 ⇒ ai2 + bi2 + ci2 + di2 = 1
( condizione di normalizzazione );
• ∫ψiψj dV = 0 ⇒ aiaj + bibj + cicj + didj = 0
( condizione di ortogonalità ).
Ibridazione sp3
È l'ibridazione tra un orbitale s e tre orbitali p che determina la formazione di 4 orbitali ibridi tutti equivalenti
ed orientati con i loro assi, in corrispondenza dei quali si ha il massimo addensamento elettronico, dal centro
ai vertici di un tetraedro regolare. Per questo motivo gli orbitali ibridi sp3 sono detti orbitali tetraedrici e l'ibridazione è detta ibridazione tetraedrica. Ad ogni orbitale ibrido concorrono per ¾ gli orbitali p e per ¼
l'orbitale s. Gli angoli dei quattro orbitali ibridi sono tutti di 109°28'. Con l'ibridazione i livelli energetici degli
orbitali cambiano e gli orbitali ibridi sp3 corrispondono tutti allo stesso livello energetico situato poco sotto
quello degli orbitali puri p. Si definisce energia di ibridazione la differenza di energia fra la configurazione
ibridizzata e quella di tetravalenza normale che si avrebbe con quattro orbitali, di cui uno s e tre p, ognuno
contenente un solo elettrone spaiato.
Ibridazione sp2
È l'ibridazione tra un orbitale s e due p che determina la formazione di tre orbitali equivalenti tra loro con i
rispettivi assi diretti dal centro ai vertici di un triangolo equilatero (quindi formano tra loro angoli di 120°).
Essi sono detti orbitali trigonali piani. Ogni orbitale ibrido ha per 2/3 carattere p e per 1/3 carattere s. Il
livello energetico degli orbitali ibridi sp2 è più basso di quello corrispondente agli orbitali sp3 a causa del
contributo percentualmente più accentuato dell'orbitale s nell'ibridazione.
Ibridazione sp
È l'ibridazione tra un orbitale s ed un orbitale p che determina la formazione di due orbitali ibridi
tra loro equivalenti coi loro assi orientati lungo la stessa retta in senso opposto. Essi sono detti
orbitali ibridi digonali. Ogni orbitale ha per ½ carattere p e per ½ carattere s. Visto la maggior
percentuale di carattere s, il livello energetico degli ibridi sp è più basso di quello sp2 ed sp3.
Ibridazione sp3d2
È la combinazione tra un orbitale s, tre orbitali p e due orbitali d dalla quale si ottiene la formazione di sei
orbitali equivalenti i cui assi sono orientati dal centro ai vertici di un ottaedro regolare. L'ibridazione è per
questo detta ottaedrica.
Teoria degli orbitali molecolari
Alla base della teoria dei legami di valenza sta la costruzione di una funzione d'onda di legame per ciascuna coppia di elettroni
condivisa fra due atomi, facendo uso dei soli orbitali atomici relativi agli elettroni che, spaiati negli atomi isolati, si accoppiano
nella formazione del legame. Gli altri orbitali atomici, anche se di energia equivalente, vengono considerati come estranei al
legame e da questo perciò non perturbati ed alterati. Invece il concetto informatore della teoria degli orbitali molecolari, certo
più valido e soddisfacente, è che quando due o più atomi interagiscono insieme legandosi tra loro, il sistema di orbitali proprio
degli atomi isolati, perturbato dall'interazione di legame, subisce una radicale trasformazione nel suo complesso, ristrutturandosi in un sistema nuovo di orbitali molecolari, cioè di orbitali rappresentativi degli elettroni degli atomi componenti su tutta l'estensione della molecola: perciò tutti gli elettroni che nella molecola sono distribuiti in orbitali estesi a due o più atomi partecipano alla realizzazione dei legami e non soltanto quelli che negli atomi di una molecola sono ripartiti in una serie di stati quantici discreti a ciascuno dei quali corrisponde una particolare funzione d'onda ψ che definisce completamente il relativo orbitale
51
molecolare. Ad ogni orbitale molecolare è associato un determinato valore di energia, che rappresenta l'energia necessaria per
allontanare dalla molecola, ionizzandola, l'elettrone che si trova nel corrispondente orbitale. I valori dell'energia relativi ai vari
orbitali molecolari individuano l'insieme dei livelli di energia elettronica caratteristici della molecola considerata. Per un elettrone che si trovi nello stato quantico corrispondente all'orbitale molecolare ψ, la funzione ψdV definisce la probabilità che
l'elettrone stesso si trovi nell'elemento di volume dV e, come per ciascuno orbitale atomico, anche per ogni orbitale molecolare
dovrà essere ∫V∞ψ2dV=1. È da osservare che le superfici rappresentative degli orbitali molecolari sono sempre policentriche,
abbracciando tutti i nuclei della molecola. Una volta definiti gli orbitali molecolari ed i relativi livelli energetici, gli elettroni si
devono considerare distribuiti nei vari orbitali, iniziando da quelli di più bassa energia, rispettando il principio di Pauli e la regola di Hund. Inoltre ogni diverso raggruppamento di atomi determina un diverso insieme di orbitali molecolari. Anche per una
molecola, le funzioni d'onda che definiscono i vari orbitali molecolari si determinano risolvendo la relativa equazione di Schrödinger. Il metodo di approssimazione più usato consiste nell'esprimere la funzione d'onda Ψ di ogni orbitale molecolare come
una combinazione lineare delle funzioni d'onda ψi degli orbitali atomici degli elettroni componenti:
Ψ = ∑ ciψi
dove le quantità ci sono dei coefficienti costanti che determinano il contributo dei singoli orbitali atomici all'orbitale molecolare
risultante. Essi sono univocamente determinati imponendo la condizione di normalizzazione. La funzione d'onda complessiva
che descrive l'insieme di tutti gli elettroni della molecola è il prodotto delle funzioni d'onda individuali relative ai singoli elettroni e l'energia elettronica totale è la somma delle energie proprie di ciascuno di essi, corrispondenti ai livelli energetici degli
orbitali occupati. È importante considerare che non tutti gli orbitali atomici si possono combinare insieme per costruire un orbitale molecolare, in quanto devono essere soddisfatte alcune condizioni fondamentali. Consideriamo per semplicità una molecola biatomica formata da due atomi A e B. Perché due orbitali atomici ψA e ψB possano tra loro combinarsi in un orbitale molecolare di legame descritto dalla funzione d'onda Ψ=cAψA + cBψB sono necessariamente da rispettare le seguenti condizioni:
1. I livelli energetici corrispondenti a ψA e ψB debbono avere valori confrontabili (cioè non troppo lontani l'uno dall'altro).
2. I due orbitali ψA e ψB alla distanza di legame debbono sovrapporsi estesamente.
3. I due orbitali ψA e ψB debbono avere la stessa simmetria rispetto all'asse di legame.
Se queste condizioni non sono verificate i due orbitali ψA e ψB non possono concorrere a formare un orbitale molecolare di legame caratterizzato da un livello energetico più basso di quello loro proprio, cioè ψA e ψB non si combinano. Quando n orbitali
atomici si combinano insieme, dalla loro combinazione derivano altrettanti orbitali molecolari a cui corrispondono livelli energetici che possono essere tutti distinti o anche in parte coincidenti (e si parlerà di orbitali molecolari degeneri). Gli orbitali
caratterizzati da livelli energetici più bassi di quelli degli orbitali atomici componenti sono detti orbitali molecolari di legame,
in quanto una diminuzione dell'energia elettronica di un insieme di più atomi rispetto agli atomi isolati indica che la loro interazione reciproca porta alla formazione di legami stabili. Gli orbitali molecolari caratterizzati invece da livelli energetici più alti
di quelli degli orbitali atomici componenti sono detti orbitali molecolari di antilegame, in quanto descrivono una distribuzione
elettronica che favorisce la separazione degli atomi l'uno dall'altro. Considerando allora una molecola AB, dalla combinazione
dei due orbitali atomici ψA e ψB, derivano due orbitali molecolari:
1. Ψl = cA(l)ψA + cB(l)ψB
2. Ψa = cA(a)ψA - cB(a)ψB
Il primo è un orbitale molecolare di legame e la sua energia è inferiore sia all'energia EA dell'orbitale atomico ψA, sia ad EB di
ψB.
Se la differenza EB-EA è molto grande, i livelli energetici degli orbitali molecolari risultanti coincidono con quelli degli orbitali
atomici di partenza e quindi ψA e ψB non danno origine ad alcun orbitale molecolare di legame. Ecco perché i livelli energetici
di ψA e ψB debbono essere vicini, cioè avere valori confrontabili. Inoltre, il livello El dell'orbitale di legame risulta tanto più
basso quanto più grande è il valore dell'integrale di sovrapposizione dato dalla equazione S = ∫V∞ψAψB dV. Quanto più estesa è
la zona di sovrapposizione, tanto più grande è il valore di S (criterio della massima sovrapposizione). Se ψA e ψB non si sovrappongono apprezzabilmente, allora S=0, cioè si conservano inalterati nelle molecole come orbitali localizzati di non legame.
Ma può essere anche S=0 per ragioni di simmetria: ecco la terza condizione. Nel caso
ψ A (s)
ψ B (p z )
in figura risulta S=0 in quanto ad ogni elemento di volume dV1 dove ψA * ψB > 0 corri+
dV 1 +
sponde un elemento di volume dV2 dove ψA * ψB < 0, cosicché i contributi reciproca+ dV 2 +
mente si annullano. Concludiamo questa introduzione con una nota sulla nomenclatura
di uso corrente nella classificazione degli orbitali molecolari: anche questi, come gli
orbitali atomici, sono caratterizzati da definiti numeri quantici: per le molecole biatomiche abbiamo un numero quantico principale n (dove n-1 corrisponde al numero di nodi della funzione d'onda) ed un numero quantico λ che definisce la componente
del momento della quantità di moto dell'elettrone lungo l'asse di legame.
• λ = 0 ⇒ orbitale σ ;
• λ = 1 ⇒ orbitale π ;
• λ = 2 ⇒ orbitale δ .
Gli orbitali di antilegame vengono segnati con un asterisco ( σ*, π*, δ* ).
52
La molecola d'idrogeno nella teoria degli orbitali molecolari
Le funzioni d'onda che rappresentano i due orbitali molecolari di H2 sono (trattandosi di due atomi uguali si ha che cAl = cBl =
N e cAa = cBa = N*):
Ψ(σ 1s)=N * [ ψA(1s) + ψB(1s) ]
Ψ(σ *1s)=N* * [ ψA(1s) - ψB(1s) ]
Le costanti N ed N* sono i fattori di normalizzazione determinati dalle condizioni di normalizzazione:
∫V∞Ψ(σ 1s)2 dV = 1
∫V∞Ψ(σ* 1s)2 dV = 1
Per l'orbitale di legame, si ottiene:
N2 ∫V∞ [ ψA(1s) + ψB(1s) ]2 dV = N2 ∫V∞ [ψA(1s)]2 dV + N2 ∫V∞ [ψB(1s)]2 dV+ 2N2 ∫V∞ [ψA(1s) ψB(1s)]2 dV=1
Essendo ciascun orbitale atomico normalizzato, cioè pari ad 1, introducendo l'integrale di sovrapposizione S=∫V∞
ψA(1s)ψB(1s)dV,
sostituendo all'equazione che è sopra, si ottiene:
1
2N2 + 2N2S = 1 ⇒ 2N2 (1+S) = 1 ⇒ N =
2(1 + S )
Per l'orbitale di antilegame, con analogo procedimento di ottiene:
1
N* =
2( 1 − S )
sicché in definitiva i due orbitali molecolari, trascurando S nel fattore di normalizzazione, diventano:
1
Ψ(σ 1s)=
* [ ψA(1s) + ψB(1s) ]
2
1
Ψ(σ* 1s)=
* [ ψA(1s) - ψB(1s) ]
2
A questi due orbitali molecolari corriE
orb. mol. di
spondono valori diversi dell'energia
antil.
variabili con la distanza internucleare. orb. at.
La curva relativa all'orbitale di legame
si abbassa al di sotto del valore dell'eorb. at.
nergia dei due atomi isolati (R=∞) ed è orb. mol.
caratterizzata da un minimo che defini- di legame
sce la distanza internucleare di equilibrio, mentre la curva di antilegame si mantiene costantemente al di sopra del valore dell'energia
degli atomi isolati e non presenta alcun minimo. Nello stato elettronico fondamentale della molecola, i due elettroni dei due atomi
saturano, con spin antiparalleli secondo Pauli, l'orbitale di legame (σ1s)2, per cui si ha un legame stabile. Se in seguito ad eccitazione uno dei due elettroni si portasse dall’orbitale di legame a quello di antilegame, l'energia complessiva risulterebbe maggiore di quella dei due atomi isolati e la molecola si dissocerebbe.
Confronto tra le due teorie
Limitandoci a considerare lo stato di più bassa energia, la funzione d'onda Ψ(1,2) relativa alla coppia di elettroni che realizza il
legame, è data secondo Heitler-London da:
Ψ(1,2) = ψΑ(1)ψΒ(2) + ψΑ(2)ψΒ(1)
mentre nella teoria degli orbitali molecolari è espressa dal prodotto di due funzioni, una ( Ψ(1) ) relativa all'elettrone 1 e la seconda ( Ψ(2) ) relativa all'elettrone 2, cioè:

ψ (A1 ) + ψ (B1 ) 

2
 Ψ(1,2 ) = Ψ(1) * Ψ( 2 ) =
1
( 2)
( 2) 
Ψ( 2 ) =
ψA + ψB 
2

Ψ( 1) =
1
[
]
[
]




1  (1) ( 2 )
(2)
(1)
(1)
(2)
(1)
( 2) 
ψ ψB + ψ A ψB + ψ A ψ A + ψB ψB 
2 A
 Heitler −London

Ioni A e B


Molecole biatomiche omonucleari
Passando a considerare le molecole biatomiche omonucleari del secondo periodo, altri orbitali atomici entrano in gioco nella
costruzione dei relativi orbitali molecolari, poiché negli atomi di questi elementi gli elettroni di valenza occupano gli orbitali 2s
e 2p. Gli orbitali 1s, per la loro estensione molto limitata attorno ai due nuclei, possono considerarsi imperturbati e costituiscono orbitali di non legame localizzati attorno ai nuclei stessi. Le relative funzioni d'onda sono:
53
Ψ(σ 2s)=
1
2
1
Ψ(σ* 2s)=
Ψ(σ 2px)=
Ψ(σ* 2px)=
Ψ(π 2py)=
Ψ(π* 2py)=
Ψ(π 2pz)=
Ψ(π* 2pz)=
2
1
2
1
2
1
2
1
2
1
2
1
* [ ψA(2s) + ψB(2s) ]
* [ ψA(2s) - ψB(2s) ]
* [ ψA(2px) + ψB(2px) ]
* [ ψA(2px) - ψB(2px) ]
* [ ψA(2py) + ψB(2py) ]
* [ ψA(2py) - ψB(2py) ]
* [ ψA(2pz) + ψB(2pz) ]
* [ ψA(2pz) - ψB(2pz) ]
2
In figura sono riportati i livelli energetici corrispondenti agli orbitali definiti
Energia
sopra: come si vede i livelli energetici degli 8 orbitali molecolari che ne risulσ∗ 2px
tano sono:
∗
σ2s < σ∗2s < σ2px < π2py = π2pz < π∗2pz = π∗2py < σ∗2px
π 2py
Se gli orbitali 2s e 2px interagiscono apprezzabilmente fra loro, gli orbitali
molecolari σ2p e π2p tendono ad invertirsi. Considerando gli elementi del 2°
π∗ 2pz
2p
2p
periodo, poiché la distanza fra i livelli energetici degli orbitali 2s e 2p aumenta con Z, è prevedibile che solo per gli elementi più pesanti, O e F, la successione degli orbitali molecolari corrisponda allo schema del diagramma, mentre
π2py
per i più leggeri si avrà l'inversione degli orbitali σ2p e π2p. Indicando con kk
i due orbitali di non legame 1s entrambi saturi:
π2pz
O2: kk (σ2s)2 (σ∗2s)2 (σ2px)2 (π2py)2 (π2pz)2 (π∗2py)2 (π∗2pz)1 (σ∗2px)1
I due elettroni che la molecola O2 ha in più rispetto ad N2 occupano a spin paσ2px
ralleli i due orbitali degeneri π∗2py e π∗2pz: di qui il paramagnetismo tipico
dell'ossigeno molecolare. L'energia di dissociazione è pari a 5,1 eV. Mentre la
σ∗ 2s
teoria dei legami di valenza nella sua stessa impostazione distingue nettamente
gli elettroni che realizzano il legame da quelli che non vi prendono parte ed è
2s
2s
perciò possibile definire la valenza come espressione del numero di legami a
cui l'atomo considerato partecipa, nella teoria degli orbitali molecolari, quando due atomi si legano tra loro, tutti gli elettroni di valenza di entrambi si distribuiscono in orbitali molecolari estendentisi sull'intera molecola e tutti,
σ2s
quindi, sono condivisi dall'uno e dall'altro atomo e partecipano insieme alla
realizzazione del legame. Tuttavia, dato che non tutti gli elettroni messi in comune dai due atomi giocano lo stesso ruolo (attrattivi quelli di legame, repulsivi quelli di antilegame) la teoria degli orbitali molecolari porta a introdurre il concetto di ordine di
legame. Questa è la differenza tra il numero di elettroni che occupano orbitali di legame ed il numero di elettroni che occupano
invece orbitali di antilegame, divisa per due. L'energia di dissociazione e la lunghezza del legame si presentano in stretto rapporto con l'ordine di legame: all'aumentare di questa, la prima cresce e la seconda diminuisce. I legami semplici (ordine di legame = 1) sono di tipo σ2, mentre i legami doppi (ordine di legame = 2) e tripli (ordine = 3) sono di tipo misto σπ e precisamente σ2π2 per i legami doppi e σ2π4 per quelli tripli.
Molecole biatomiche eteronucleari
Ad ogni orbitale molecolare, gli orbitali componenti dei due atomi concorrono con peso diverso: se esso è di legame concorre
con maggior perso l'orbitale atomico dell'atomo più elettronegativo, mentre la situazione si inverte per gli orbitali di antilegame. Consideriamo la molecola HF: le funzioni d'onda dei due orbitali molecolari di legame ed antilegame sono:
Ψ(σ) = N [ ψH(1s) + λψF(2px) ]
Ψ(σ∗) = N* [ ψH(1s) - λ'ψF(2px) ]
La distribuzione elettronica dell'orbitale molecolare di legame è asimmetrica con maggior addensamento verso F più elettronegativo, così come lo è quella dell'orbitale di antilegame, con maggior addensamento verso H meno elettronegativo.
54
Strutture tipiche di composti
• I° gruppo: gli elementi del primo gruppo sono caratterizzati da composti tipicamente ionici. Interessanti strutture covalenti
si hanno in composti di coordinazione.
• II° gruppo
• Berillio: tra i più semplici composti covalenti citiamo l'idruro BeH2 ed il cloruro BeCl2. L'atomo di berillio ha molto accentuata la tendenza a realizzare non due, ma quattro legami, coordinandosi ad atomi donatori, avendo per
questo disponibili nella configurazione nella configurazione elettronica 2s12p1 due orbitali vacanti.
• III° gruppo
• Boro: il boro nel suo stato normale di trivalenza riferibile alla configurazione elettronica 2s12p2 realizza strutture
corrispondenti allo stato di ibridazione trigonale sp2 o anche ibridazione tetraedrica sp3.
• Alluminio: non dà come il boro composti semplici a struttura trigonale piana. Gli alogenuri hanno molecole dimere, vale a dire doppie come Al2X6 nelle quali ogni atomo di alluminio è circondato tetraedricamente da quattro atomi di alogeno.
• IV° gruppo
• Carbonio: le strutture dei composti innumerevoli del carbonio, inorganici ed organici, sono riferibili ai tre tipi di
ibridazione sp3, sp2 ed sp propri dello stato di trivalenza dell'atomo. Anche allo stato elementare il carbonio è caratterizzato da due forme cristalline diverse, il diamante e la grafite: nel diamante ogni atomo di carbonio è circondato tetraedricamente da altri quattro atomi, essendo i legami determinati da orbitali ibridi di tipo sp3 reciprocamente sovrapposti; nella grafite l'ibridazione trigonale di tipo sp2 determina la formazione di piani d'atomi di carbonio a maglie esagonali, essendo gli angoli di legame di 120°. Ne deriva una tipica struttura a strati con legami
forti fra atomo ed atomo entro ogni strato e legami deboli fra strato e strato e quindi caratterizzata da una accentuatissima sfaldabilità parallelamente ai piani reticolari.
• Ibridazione sp3: è questo lo stato di ibridazione proprio del carbonio nel metano (CH4) ed in tutti i composti organici saturi, cioè non contenenti legami multipli. Ogni atomo di carbonio è circondato tetraedricamente dai quattro atomi a cui è legato tramite orbitali ibridi di tipo sp3.
• Ibridazione sp2: questo tipo di ibridazione è proprio di ogni atomo di carbonio che nella struttura molecolare considerata sia legato con un legame doppio ad un altro atomo. L'etilene (C2H4) è il più semplice tra
gli idrocarburi alifatici non saturi con doppi legami ( serie etilenica ). Il benzene (C6H6) è il capostipite
di una vastissima serie di composti organici detti aromatici: i sei atomi di carbonio utilizzano orbitali ibridi di tipo sp2 per legarsi tra loro e con altrettanti atomi di idrogeno, realizzando un insieme di legami di
tipo σ che determinano la struttura esagonale regolare propria di questa molecola. L'interazione effettiva
tra i sei elettroni pz è esprimibile in termini di risonanza fra le strutture limiti, corrispondenti alle formule
di Kekulè e di Dewar. Per quel che riguarda, infine, lo ione carbonato, che citiamo come ultimo esempio
di ibridazione sp2, la sua struttura è quella di un triangolo equilatero con al centro l'atomo di carbonio.
• Ibridazione sp: è questo lo stato di ibridazione proprio di ogni atomo di carbonio legato ad un altro atomo
con un legame triplo o a due atomi con due legami doppi. Come esempi semplici citiamo l'acetilene
(C2H2) ed il diossido di carbonio (CO2). L'acetilene è il più semplice idrocarburo della serie alifatica non
satura caratterizzata dalla presenza di tripli legami carbonio-carbonio ( serie acetilenica ). Anche nella
molecola di diossido di carbonio l'atomo si trova nello stato di ibridazione digonale.
• Silicio: le ragguardevoli dimensioni atomiche del silicio impediscono la formazione di legami di tipo π che i tipi di
ibridazione sp2 ed sp comporterebbero. Ogni suo atomo è sempre legato ad almeno altri quattro atomi realizzando
configurazioni di tipo tetraedrico, riferibili all'ibridazione sp3. Questo è lo stato di ibridazione proprio del silicio
non solo negli idruri ( i cosiddetti silicani come SiH4, Si2H6 ) o negli alogenuri (come SiCl4), ma anche nel diossido (SiO2) e nei suoi derivati ( i cosiddetti silicati ). Il diossido ha una struttura continua tridimensionale.
• V° gruppo
• Azoto: l'atomo di azoto nella configurazione dello stato fondamentale 1s22s22p3 ha tre elettroni non accoppiati che
determinano la tipica trivalenza propria dell'elemento nei suoi composti più semplici. Alla ibridazione di tipo sp2
degli orbitali di valenza dell'atomo nello stato positivo N+ è riferibile la struttura dello ione nitrato NO3-. Citiamo
come altro esempio il pentaossido di diazoto N2O5, tradizionalmente noto come anidride nitrica. Questo composto
solido, cristallino a temperatura ambiente, ha struttura ionica.
• Fosforo, Arsenico, Antimonio: gli elementi che seguono l'azoto nel V° gruppo ne differiscono principalmente perché nei loro composti possono utilizzare anche orbitali d, col cui contributo la loro covalenza può salire a 5 o anche a 6. Date le notevoli dimensioni dei loro atomi, essi formano legami π solo con l'intervento degli orbitali nd.
Quindi il fosforo, l'arsenico, l'antimonio ed il bismuto non costruiscono strutture molecolari corrispondenti alle ibridazioni sp2 ed sp tipiche di importanti composti dell'azoto. Allo stato di vapore, fin circa a 800°C, il fosforo è
costituito da molecole tetraatomiche P4 che a temperature più alte si dissociano: in esse gli atomi di fosforo sono
situati ai vertici di un tetraedro regolare. Allo stato solido il fosforo può esistere in diverse forme cristalline (modificazioni allotropiche) che si differenziano tra loro per la diversa struttura. Il fosforo bianco, instabile a temperatura ambiente, è molto reattivo e tossico. È costituto da cristalli molecolari ove singole molecole P4 sono tenute insieme da forze di Van Der Waals. La forma più stabile del fosforo solido è il cosiddetto fosforo nero. Altra forma
55
molto comune è il fosforo rosso, inerte e non tossico, con struttura disordinata, ma simile al fosforo nero. Citiamo
come composti la fosfina PH3, lo ione fosfonio PH4+, l'arsinia AsH3, la stibina SbH3. Hanno struttura tetraedrica
(ovviamente non regolare) i composti del tipo X3PY (con X= F, Cl, Br e Y= O, S) come l'ossocloruro Cl3PO ove
l'atomo di fosforo forma quattro legami ibridi di tipo sp3 ed un legame π con un orbitale di tipo d.
• VI° gruppo
• Ossigeno: l'ossigeno, per la sua configurazione elettronica e la non disponibilità di orbitali liberi di sufficientemente bassa energia atti alla promozione di elettroni dagli orbitali 2s o 2p, è un elemento tipicamente bivalente. Se assume una carica negativa, un atomo di ossigeno forma un solo legame, come nello ione idrossido OH-, mentre se
assume una carica positiva e diviene così isoelettronico con l'atomo neutro di azoto, forma tre legami, come nello
ione ossonio H3O+. Le forme di ibridazione da considerare sono del tipo sp3 e sp2: dalla prima derivano strutture
piramidali trigonali (H3O+) o angolari (H2O), mentre dalla seconda strutture angolari come l'ozono O3. Riguardo
alla molecola d'acqua è da rilevare un elevato valore dell'angolo fra i due legami O-H ( = 104,5°). Anche qui dunque, come negli idruri del V gruppo, col crescere delle dimensioni atomiche, l'angolo fra le direzioni dei legami
diminuisce, allontanandosi sempre più dal valore proprio delle direzioni tetraedriche ( = 109,5°). L'ossigeno forma,
oltre all'acqua, anche un altro importante idruro: il perossido di idrogeno H2O2, noto correntemente con il nome di
acqua ossigenata. Per entrambi gli atomi di ossigeno si ha da considerare lo stato di ibridazione sp3. La struttura
dell'ozono O3 ha un angolo fra i due legami ossigeno-ossigeno non molto lontano da 120°. Questo implica per l'atomo d'ossigeno centrale uno stato di ibridazione di tipo sp2,
• Zolfo: numerosissimi sono i composti dello zolfo e varie le loro strutture. Allo stato elementare può trovarsi in due
diverse modificazioni cristalline, rombica l'una e monoclina l'altra, stabile la prima a temperatura ambiente fino a
95,6°C, mentre la seconda al di sopra di questa temperatura. Lo zolfo può utilizzare, per la formazione di legami,
orbitali d, che corrispondono ad un livello energetico non molto distante da quello degli orbitali 3s e 3p. L'atomo
di zolfo, già notevolmente elettronegativo, può anche accogliere due elettroni per formare lo ione S2-, stabile nei
solfuri a natura ionica dei metalli alcalini ed alcalino-terrosi, molto elettropositivi: i solfuri degli elementi meno elettropositivi hanno invece struttura covalente (tetraedrica ed ottaedrica). Tra gli ossidi citiamo il triossido SO3 ed
il diossido SO2, designati molto spesso con le denominazioni rispettivamente di anidride solforica e solforosa. La
struttura delle loro molecole, trigonale piana la prima ed angolare la seconda, è da riferire al tipo di ibridazione
sp2. Il triossido è un solido cristallino a struttura molecolare, il diossido è gassoso a temperatura ambiente. La sua
molecola ha struttura angolare con un angolo tra i due legami S-O di circa 120°.
• VII° gruppo: è questo il gruppo della famiglia tipica degli alogeni, caratterizzati, in ogni periodo, dai valori più alti di elettronegatività: questi decrescono regolarmente dal fluoro allo iodio. Gli alogenuri di idrogeno ( HF, HCl, HBr, HI ) sono
costituiti da molecole covalenti con legami notevolmente polari: se si eccettua il primo, liquido a temperatura ambiente, tutti
gli altri sono gassosi. Mentre il fluoro è sempre e soltanto monovalente, non essendo possibile la promozione di elettroni
dagli orbitali 2p o 2s ad orbitali successivi liberi, per i loro livelli energetici sfavorevolmente alti, gli altri alogeni, a causa
della disponibilità di orbitali d a livelli energetici non troppo alti, sono caratterizzati anche da stati di valenza superiore. Così accanto a perclorati ed a periodati come KClO4 e KIO4, composti importanti nella chimica del cloro e dello iodio, solo di
recente si è riusciti ad ottenere con molta difficoltà lo ione perbromato.
• Gruppo 0: questo è il gruppo che contiene i cosiddetti gas nobili. La notevole inerzia chimica di questi elementi, che risalta
al confronto della reattività con gli altri elementi, è conseguenza della stabilità particolarmente notevole della loro configurazione elettronica, che più volte abbiamo avuto occasione di sottolineare.
Il legame metallico
Sono metalli tutti gli elementi di transizione e quelli posti prima della linea di demarcazione, ad eccezione di Ge, Sb, Po che
sono semimetalli. Le proprietà metalliche sono:
1. Conducibilità elettrica: applicando una d.d.p. anche molto piccola ad un metallo si ha passaggio di corrente, cioè si origina
un flusso di elettroni. Ciò vuol dire che nella struttura del metallo sono presenti elettroni liberi di muoversi. All'aumentare
della temperatura la conducibilità elettrica diminuisce in quanto aumenta la resistenza R=V/I, poiché il moto degli elettroni
liberi viene ostacolato dalla progressiva esaltazione delle oscillazioni degli atomi e dal conseguente crescere del numero
degli urti.
2. Effetto fotoelettrico e termoionico: la presenza di elettroni relativamente liberi perché solo debolmente legati agli atomi del
reticolo cristallino è dimostrata dalla facilità con cui essi possono essere estratti dalla superficie metallica, irraggiandola con
una luce di una determinata lunghezza d'onda (effetto fotoelettrico) o riscaldandola (effetto termoionico).
3. Conducibilità termica: se si considera un filare di atomi di carattere metallico si ha che essi oscillano attorno a definite posizioni di equilibrio tanto più velocemente quanto più alta è la temperatura. Se si pone il filare vicino ad una sorgente di calore, questa trasmette energia termica al primo atomo, il quale inizia ad oscillare più forte trasmettendo energia a quello più
vicino e così via. Il progressivo trasferimento di energia cinetica attraverso il filare di atomi determina il graduale aumento
della temperatura di tutto il cristallo metallico.
56
4. Duttilità e malleabilità: i metalli possono subire numerevoli deformazioni permanenti prima di rompersi, così da lasciarsi
ridurre in fili sottili (duttilità) o in lamine sottili (malleabilità). Ciò vuol dire che i piani reticolari possono slittare facilmente
gli uni agli altri, senza alterare le interazioni di legame tra atomi.
5. Proprietà ottiche: i metalli hanno una lucentezza caratteristica, cioè assorbono tutte le radiazioni incidenti e le rimettono in
tutte le direzioni. Ciò vuol dire che, assorbendo energia, gli elettroni passano a livelli energetici superiori per poi tornare al
livello primitivo rilasciando energia sotto forma di fotoni che diffondono in ogni direzione.
6. Elettropositività: i metalli sono tendenzialmente elettropositivi, cioè hanno la tendenza a dare ioni positivi.
7. Struttura cristallina: esse sono caratterizzate da numeri di coordinazione molto elevati e le più tipiche sono la cubica a corpo centrato (8), la cubica a facce centrate (12) e l'esagonale compatta (12). Inoltre la compattezza e la coesione dei legami
metallici implica che i legami fra gli atomi sono molto forti. Esse non possono essere interpretate né sulla base di un modello elettrostatico (cristalli a struttura ionica) , né sulle interazioni dovute a forze di Van Der Waals, troppo deboli, né sulla
base di legami covalenti localizzati (determinate da coppie elettroniche in compartecipazione fra un atomo e quelli circostanti). Quindi per concepire un così gran numero di legami, gli elettroni non si possono concepire localizzati, ma delocalizzati. Allora si può pensare il reticolo cristallino formato da ioni positivi immersi in una nube di elettroni mobili, diffusa per
tutto il reticolo. Gli elettroni mobili sono quelli degli strati più esterni, cioè gli elettroni di valenza, mentre gli altri sono localizzati attorno al nucleo. La nuvola elettronica diffusa determina i legami tra gli atomi e tutte le proprietà metalliche finora
descritte. La delocalizzazione degli elettroni nei cristalli metallici può essere interpretata sia con la teoria degli orbitali molecolari, sia con quella dei legami di valenza visti in precedenza.
Reticoli cristallini tipici dei metalli
I reticoli cristallini tipici della maggior parte dei metalli sono caratterizzati da un impacchettamento di atomi molto compatti ed
i modelli fondamentali sono tre:
1. struttura esagonale compatta
2. struttura cubica a facce centrate
3. struttura cubica a corpo centrato
Le denominazioni derivano dalla forma della cella elementare le cui ripetizioni nelle varie direzioni dello spazio determina il
reticolo cristallino. Nel primo caso la cella elementare ha la forma di un prisma esagonale con un atomo in ogni vertice e tre
atomi all'interno. Nel secondo e nel terzo è un cubo. Le prime due strutture sono più compatte della terza e sono i modi con cui
si può realizzare il massimo addensamento nel disporre un insieme di sfere di ugual volume l'una accanto all'altra in strati successivi. In essi gli spazi vuoti sono ridotti al minimo (26 %), mentre nella terza struttura si ha un 32 %. Sia nella struttura esagonale compatta che in quella cubica a facce centrate ogni atomo è a contatto con 12 atomi (n°. coordinazione =12) mentre
nella cubica a corpo centrato ogni atomo è a contatto con 8 atomi. Molti metalli, poi, sono polimorfici, cioè caratterizzati da
strutture diverse in funzione di temperatura e pressione a cui sono sottoposti.
57
La teoria degli orbitali di Bloch
Il modello a banda si applica a tutti i solidi cristallini metallici o no, ed è efficace per interpretare le loro proprietà di conduttori
o isolanti elettrici. Considerando un metallo e distribuendo gli elettroni sui livelli permessi si possono verificare le seguenti situazioni: gli orbitali corrispondenti alla banda di valenza sono in entrambi i casi delocalizzati e gli elettroni che li occupano sono perciò liberi di spostarsi da un atomo ad un altro, ma l'effetto di un campo elettrico applicato è diverso nei due casi. Il camLe proprietà e la struttura dei metalli rivelano che gli elettroni di valenza dei loro atomi sono delocalizzati, cioè diffusi per tutta l'estensione del reticolo cristallino, liberi di muoversi anche sotto l'azione di un campo elettrico molto debole. Quindi la descrizione della struttura elettronica dei metalli può essere impostata sulla teoria degli orbitali molecolari. Considerando un cristallo metallico come una molecola gigante, per la compattezza della sua struttura, esistono le condizioni perché si realizzi un
esteso ricoprimento degli orbitali di valenza dei singoli atomi, così che gli orbitali cristallini o reticolari risultanti sono completamente delocalizzati ed abbracciano tutto il reticolo. Questi orbitali delocalizzati, che descrivono la distribuzione degli elettroni di valenza degli atomi nel reticolo cristallino di un metallo, sono generalmente designati come funzioni d'onda di Bloch. Gli
orbitali reticolari di un metallo differiscono da quelli propri di una molecola per una caratteristica molto importante relativa ai
livelli energetici ad essa corrispondenti. Se si immagina di costruire un reticolo cristallino quando ad un primo atomo A se ne
aggiunge un secondo B, i due orbitali di valenza dei due atomi si combinano insieme determinando due orbitali molecolari
ψΑ+ψΒ e ψΑ−ψΒ ciascuno con una sua propria energia, più bassa di quella degli orbitali atomici originari per il primo e più alta
per il secondo. Se ora viene addizionato un terzo atomo gli orbitali molecolari di valenza determinano tre orbitali molecolari e
così via. Un'aggiunta di un nuovo atomo fa aumentare di uno il numero di orbitali molecolari risultanti e dei corrispondenti livelli energetici, quindi per un insieme di N atomi si avranno N orbitali molecolari ed N livelli energetici. Se N è molto grande,
dell'ordine di 1023, i livelli sono così ravvicinati da costituire una banda di energia continua. Ad ogni orbitale atomico di un
singolo atomo corrisponde nel cristallo una banda di livelli energetici e le proprietà del cristallo sono determinate dalla differenza di energia tra le successive bande e dalla distribuzione in esse degli elettroni. La larghezza delle bande risultanti dalle interazioni tra gli atomi nel cristallo e la separazione tra l'una e l'altra, dipendono dalla distanza internucleare e mano a mano che
essa diminuisce, aumenta la larghezza della banda e si riduce la separazione tra l'una e l'altra. Diminuendo la distanza interatomica ogni livello origina una banda che si allunga con la reciproca interazione tra gli atomi. Inoltre per una data distanza r tra
gli atomi, le bande sono tanto più allargate quanto più alta è la loro energia ed il progressivo allargamento delle bande con il
diminuire della distanza interatomica può determinare la loro sovrapposizione. Gli elettroni degli atomi del cristallo si distribuiscono negli orbitali corrispondenti a livelli energetici delle varie successive bande secondo il principio di Pauli, cominciando da quella a più bassa energia. Quindi gli elettroni degli orbitali 1s, 2s, 2s saturano le corrispondenti bande interne, mentre
gli elettroni di valenza 3s saturano i primi N/2 livelli della banda di valenza. La successione delle varie bande ad energia crescente è intervallata da fasce di valori proibiti per gli elettroni del cristallo. Gli elettroni che occupano le bande interne sono
praticamente localizzati entro gli atomi a cui appartengono, mentre quelli della banda di valenza sono delocalizzati nel senso
che
possono
muoversi
per
tutta
l'estensione
del
reticolo.
Energia
Banda
vuota
Banda
vuota
Banda di
valenza
non satura
Banda di
valenza
satura
Bande interne
sature
Caso A
Caso B
po elettrico applicato tende a convogliare gli elettroni liberi in un flusso unidirezionale che comporta un aumento dell'energia
degli elettroni che vi partecipano. Nel caso A questo può essere realizzato perché la banda di valenza ha livelli energetici disponibili al di sopra di quelli occupati in assenza di un campo elettrico e ad essi un campo elettrico anche debole può promuovere un flusso ordinato nella propria direzione. Nel caso B questo è impossibile perché la banda di valenza è completamente
satura con gli elettroni che si muovono in tutte le direzioni senza la possibilità di essere trascinati nella direzione del campo per
la mancanza di livelli più alti disponibili. Nel primo caso il cristallo è un conduttore perché il flusso di elettroni crea il passaggio di corrente che si rileva macroscopicamente, nel secondo caso il cristallo è un isolante, in quanto il flusso di elettroni è impedito e quindi non si crea nessuna corrente. L'unico modo per farlo diventare conduttore sarebbe quello di applicargli un campo elettrico molto forte tale che una parte degli elettroni di valenza vengono fatti passare dalla banda di valenza satura alla banda di conduzione. In generale si può dire che se un cristallo è caratterizzato da bande completamente piene e bande completamente vuote senza reciproche sovrapposizioni, allora esso si comporterà come un isolante. È da notare però che l'assetto del58
l'insieme delle bande elettroniche e la loro successione ed eventuali sovrapposizioni sono determinati non solo dai livelli energetici degli atomi che compongono il reticolo e dalla distanza internucleare, ma anche dalla struttura del reticolo cristallino. A
tale scopo consideriamo il caso del diamante in cui gli atomi di carbonio sono legati tra loro in un reticolo covalente con coordinazione tetraedrica determinata da orbitali ibridi sp3. I quattro orbitali ibridi sono isoenergetici e la loro combinazione con
quelli di un altro atomo porta alla formazione di due orbitali molecolari di legame e di antilegame. Quindi per un insieme di N
atomi gli orbitali molecolari risultanti sono 4N, distinti in due raggruppamenti di legame e di antilegame contenenti ciascuno
2N orbitali i cui livelli energetici si raccolgono in due bande separate da un largo intervallo proibito. La banda inferiore è completamente saturata dagli elettroni di valenza e quella superiore completamente vuota e ad essa non può accedervi nessun elettrone per la grande distanza fra le due bande. La situazione è molto simile anche a quella del silicio, solo che la distanza tra le
due bande è molto più piccola, cosicché è possibile il trasferimento di un certo numero di elettroni dall'una all'altra o per eccitazione termica (termoconduzione) o per irraggiamento con radiazioni di adatta lunghezza d'onda (fotoconduzione). Le sostanze
cristalline che hanno questa caratteristica vengono dette semiconduttori intrinseci. Con il trasferimento di elettroni dalla banda
di valenza alla successiva banda di conduzione, vengono a partecipare alla conduzione di corrente gli elettroni di entrambe le
bande, in quanto entrambe vengono ad avere livelli energetici vacanti. La conduzione determinata dagli elettroni della banda di
conduzione che precedentemente era vuota viene detta di tipo n, mentre quella dovuta agli elettroni della banda di valenza non
più satura è detta di tipo p, in quanto viene trattata come il moto delle lacune positive lasciate dagli elettroni strappati dal campo elettrico e portati nella banda di conduzione. Quindi il movimento degli elettroni della banda di valenza, sotto l'azione di un
campo elettrico, equivale alla migrazione in direzione opposta delle lacune. La conducibilità dei semiconduttori, a differenza
dei metalli, aumenta con la temperatura, in quanto crescendo questa, cresce anche il numero di elettroni che dalla banda di valenza si trasferiscono alla banda di conduzione. La conduzione di un metallo semiconduttore può essere influenzata con l'aggiunta di piccolissime quantità di elementi estranei detti droganti ed anche un cristallo isolante, se opportunamente drogato,
può acquistare le caratteristiche di un semiconduttore. Il caso più comune di droganti è dato dalle cosiddette impurezze sostituzionali, cioè di atomi di altri elementi che vanno a sostituirsi ad atomi del reticolo cristallino. Con l'introduzione degli atomi del
drogante, nuovi livelli elettronici permessi, detti livelli di impurezza, vengono ad interporsi tra la banda di valenza e quella di
conduzione nell'intervallo vietato. Se gli atomi introdotti hanno più elettroni di valenza di quelli del reticolo ospitante, essi agiscono da donatori di elettroni, se invece ne hanno meno agiscono da accettori di elettroni.
Silicio, semiconduttori
Il silicio ha la stessa struttura del diamante (sp3), dunque per questo elemento si ha una situazione simile. In questo caso però
tra le due bande elettroniche c'è meno separazione (∆E = 1,12 eV) rispetto al carbonio. Ciò perché negli orbitali del silicio c'è
meno sovrapposizione rispetto a quelli del carbonio. In generale si ha la seguente classificazione:
• ∆E < 0,2 eV ⇒ buoni conduttori
• 0,2 < ∆E < 2,5 eV ⇒ semiconduttori
• ∆E > 2,5 eV ⇒ isolanti
Cosa avviene nel reticolo al variare della temperatura? Se aumentiamo la temperatura aumentano le vibrazioni, finché un elettrone ha un'energia tale da poter saltare dalla banda di valenza alla banda di conduzione. Man mano che aumenta la temperatura, la probabilità che ciò avvenga aumenta. Se l'elettrone riesce a staccarsi comincia a vagare per il reticolo cristallino. Questo
equivale al passaggio dell'elettrone dalla sommità della banda di valenza alla coda della banda di conduzione. In questo modo
nella banda di valenza resta una lacuna che equivale ad una carica positiva. La lacuna tende a spostarsi, perché altri elettroni la
riempiono lasciando a loro volta una lacuna dietro di loro e questo spostamento risulta in direzione opposta a quella dell'elettrone che l'ha generata. Quindi l'elettricità si trasmette in due maniere: con gli elettroni e con le lacune. Si noti tuttavia che la
trasmissione tramite lacune è più difficoltosa in quanto gli elettroni, per riempire le lacune, devono vincere delle forze di interazione che li legano agli atomi. Esiste una relazione tra energia di legame e gap di energia proibita: più forte è il legame ( e
quindi più orbitali sono sovrapposti) più il gap di energia proibita è alto. Nella banda di valenza gli elettroni sono localizzati,
ma non del tutto, mentre nella banda di conduzione la distribuzione è circa uniforme, cioè sono delocalizzati. La resistenza al
passaggio di corrente elettrica dipende dalla oscillazione degli elettroni, che possono fare più o meno ostacolo al flusso. Aumentando la temperatura aumenta di conseguenza anche la resistenza.
Drogaggio
È detto drogaggio l'inserzione nel reticolo cristallino di un elemento (solitamente semiconduttore) di opportuni atomi o impurezze che ne variano la resistenza al passaggio di corrente. Esistono due tipi di drogaggio:
1. Drogaggio n. Il silicio ha quattro elettroni di legame, ma il fosforo ne ha cinque. Il fosforo si adatta nel reticolo, ma resta un
elettrone in più che è solo debolmente legato all'atomo, per cui basta fornire poca energia per farlo migrare, col fosforo che
si carica positivamente. Drogando col fosforo, si forma un livello nuovo nel ∆E, tra la banda di valenza e la banda di conduzione e più spostato verso quest'ultima. Importante notare anche il crollo della resistività: nel silicio puro si ha R=104
Ωcm, nel silicio drogato al 5‰ si ha invece R=10-3 Ωcm. Questi si chiamano semiconduttori di tipo n.
2. Drogaggio p. In questo tipo di drogaggio si usa un elemento del III° gruppo, il genere il boro. Questi elementi hanno solo la
possibilità di fare tre legami (hanno un elettrone periferico in meno rispetto al silicio). Dunque per fare il quarto legame, il
59
boro strappa un elettrone ad un atomo di silicio vicino, creando in questo una lacuna positiva. La resistività crolla anche in
questo caso. Il materiale semiconduttore non drogato si dice semiconduttore intrinseco.
Legami con interazioni di Van Der Waals
Sono indicate genericamente con interazioni di Van Der Waals le forze attrattive tra molecole neutre. Queste sono attive, anche
se con intensità diversa, sia nei gas, sia nei liquidi, sia nei cristalli molecolari. Si tratta di interazioni deboli a corto raggio, perché sono significative solo a distanza molto ravvicinata tra le molecole, di natura elettrostatica. Esse sono riconducibili a tre
schemi fondamentali di interazioni:
1. interazione fra dipoli permanenti
2. interazione fra un dipolo permanente ed un dipolo indotto
3. interazione fra molecole apolari
In un insieme di molecole polari (assimilabili a dipoli elettrici), le forze intermolecolari sono determinate dal contemporaneo
concorso di interazioni corrispondenti a tutti questi tre tipi. Per le molecole apolari, invece, i primi due non possono ovviamente essere chiamati in causa. Il primo tentativo di calcolo fu di Keenson per le interazioni tra dipoli permanenti considerando gli
effetti opposti per le forze di natura elettrostatica che tendono ad orientare i dipoli in modo che all'estremità positiva di ciascuno si avvicini quella negativa dei contigui e della agitazione termica che ostacola l'azione orientatrice di quelle forze. Nel gioco
concomitante dei due opposti effetti, prevale in media la configurazione attrattiva che determina un'energia media detta effetto
di orientazione dato da:
4
2µ
1
E OR = −
* 6
3kΤ r
Debye estese la teoria tenendo conto del fatto che una molecola polare induce sempre un dipolo in qualunque altra molecola
che le si avvicini (effetto induttivo): il dipolo indotto è funzione della polarizzabilità α della molecola. Questo effetto va sempre
considerato unitamente al precedente e produce un incremento dell'energia detto effetto di induzione dato da:
2
2αµ
E IND = − 6
r
Le interazioni attrattive tra molecole apolari, infine, sono state trattate da London, grazie alla meccanica quantistica: considerando le molecole monoatomiche di un gas inerte, la nuvola elettronica attorno al nucleo è perfettamente simmetrica solo se ne
viene considerata la distribuzione media nel tempo, perché in un dato istante, per il moto degli elettroni, essa si rivelerebbe
spesso asimmetrica e quindi tale da determinare un momento dipolare variabile. Ciascun dipolo istantaneo genera un campo
elettrico che polarizza le molecole circostanti, inducendovi un momento dipolare variabile.
L'equazione di London esprime questo effetto di dispersione :
2
3 E ION α
EL = −
6
4 r
L'espressione completa dell'energia intermolecolare deve includere anche un termine repulsivo che diventa apprezzabile solo a
distanze estremamente brevi, causato dalla sovrapposizione delle nuvole elettroniche delle molecole (energia di sovrapposizione). Questo è quindi detto effetto di sovrapposizione:
EREP = C * r-n
dove C è costante ed n varia da 9 a 12. L'equazione finale è quindi:
EINTERM = EOR + EIND + EL + EREP
dove i primi tre addendi indicano energie di attrazione e l'ultimo indica una repulsione.
Legame ad idrogeno
Se in una molecola un atomo di idrogeno si lega ad un atomo X molto elettronegativo, il legame che si forma ha un carattere
polare molto accentuato e l'atomo di idrogeno elettropositivo può intervenire con un altro atomo elettronegativo Y di un'altra
molecola formando un legame intermolecolare, o della stessa molecola formando un legame intramolecolare X-H...Y. L'atomo
di idrogeno fa da ponte tra i due atomi e, per le dimensioni molto piccole, il campo elettrico nel suo intorno è molto intenso e
questo determina il legame con l'atomo Y fortemente elettronegativo, così da trovarsi serrato tra i due atomi X e Y di dimensioni molto maggiori, in modo che il loro ingombro non consenta ad altri atomi si avvicinino all'atomo di idrogeno. Il legame a
idrogeno è molto debole ed è caratteristico della struttura dell'acqua e della maggior parte dei sistemi biologici. Nell'acqua le
molecole si aggregano tramite ponti ad idrogeno. Nel ghiaccio i legami tra molecola e molecola determinano una struttura esagonale notevolmente aperta, che comporta una densità minore di quella dell'acqua liquida così che quando il ghiaccio fonde,
viene demolito il reticolo ed il volume diminuisce fino a che, con l'aumentare della temperatura, non comincia a prevalere l'effetto dell'espansione dovuto alle oscillazioni molecolari. Il massimo della densità si raggiunge a 4°C. Il legame ad idrogeno, pur
essendo debole, influisce molto sulle proprietà fisiche e chimiche del composto, come ad esempio l'aumento del calore di fusione e vaporizzazione. Grande importanza ha il legame a idrogeno in biologia per il suo ruolo determinante riguardo alla struttura ed alle proprietà delle proteine e degli acidi nucleici.
60
I tre stati di aggregazione della materia
Introduzione
Lo stato solido è caratterizzato da una struttura ordinata delle particelle (ad eccezione dei vetri e delle materie plastiche) che
legandosi tra loro formano una struttura cristallina tipica della sostanza considerata, nelle quali esse oscillano continuamente
attorno a definite posizioni di equilibrio con una velocità che aumenta al crescere della temperatura. Così i solidi sono caratterizzati da una notevole rigidità, per la quale hanno volume e forma propria e per essere deformati richiedono l'applicazione di
notevoli forze. Nello stato liquido le forze intermolecolari sono ancora rilevanti, ma meno intense che nello stato solido, per cui
si ha una distribuzione disordinata delle particelle nella quale possono permanere zone limitate dove si conserva ancora un certo ordine detto ordine a corto raggio. Nello stato gassoso scompare ogni traccia di ordine e le molecole si muovono libere per
tutto lo spazio ad esse concesso. I liquidi ed i gas per la loro mobilità di molecole e possibilità di spostamento, sono detti fluidi.
Allo stato solido gli atomi sono trattenuti in definite posizioni, attorno alle quali compiono delle oscillazioni limitate dalle forze
di legame. Quando le oscillazioni diventano così energetiche da vincere le forze di legame alle quali è dovuta la stabilità del
reticolo cristallino, esso si sfascia e fonde allo stato liquido. Continuando a somministrare calore al liquido, accresce l'energia
cinetica dei moti molecolari fino a che il liquido non vaporizza, passando allo stato gassoso. A volte dallo stato solido si passa
direttamente allo stato gassoso attraverso una trasformazione chiamata sublimazione. Ogni trasformazione di stato è accompagnata da una variazione di energia che si manifesta come calore assorbito o sviluppato a seconda della trasformazione ed esso
viene detto calore latente. I processi di fusione e vaporizzazione sono endotermici, cioè assorbono energia dall’esterno perché
partono da stati con legami intermolecolari forti per arrivare a stati con legami deboli. I processi inversi di solidificazione e
condensazione, portando alla formazione di legami più forti di quelli di partenza, sono esotermici, cioè sprigionano energia.
Lo stato gassoso
I gas sono i sistemi chimici più semplici, in quanto il loro comportamento a pressione sufficientemente basse tende ad essere
uniforme indipendentemente dalla natura del gas. Per essi, in queste situazioni, valgono leggi esatte e particolarmente semplici.
Essi vengono detti gas perfetti o ideali e sono da considerare come un modello limite al quale ogni gas si avvicina se sufficientemente rarefatto. Un sistema gassoso è sempre individuato da un'equazione di stato del tipo f(p,T,V)=0 che lega fra loro le variabili che definiscono il sistema. Per un gas ideale, tale equazione assume:
lim pVn = f ( T )
p→0
pVn
= cos tan te
T
Il valore della costante al limite è indicato con ℜ, quindi per n moli di gas in un volume si ha:
m
−1
−1
pV = nℜT =
ℜT ⇒ ℜ = 8, 31J ⋅ moli ⋅ K = 0, 082 atm .
M
che raccoglie le leggi di Boyle, di Gay-Lussac, di Avogadro e di Dalton:
1.
Legge di Boyle: se T è costante, pV=cost. ⇒ p1V1 = p2V2 (isoterme);
2.
Leggi di Gay-Lussac:
a)
se p ed n sono costanti, V/T = cost. ⇒ V1/T1 = V2/T2 (isobare);
b)
se V ed n sono costanti, p/T = cost. ⇒ p1/T1 = p2/T2 (isocore);
3.
Legge di Avogadro: volumi uguali di gas diversi nelle stesse condizioni di pressione e temperatura contengono un ugual numero di molecole. pV=n1ℜT e pV=n2ℜT ⇒ n1 = n2 . Per n=1, T=273 K, p=1 atm. ⇒ 22,4 l⋅moli-1 ;
4.
Legge di Dalton: pV = nℜT = (n1 + n2 + ... + nn) ℜT ⇒ p = n1 ℜT/V + ... + nn ℜT/V = p1 + p2 + ... + pn.
La pressione totale è pari alla somma delle pressioni parziali. La pressione parziale di un componente è data dal prodotto tra la
pressione totale e la frazione molare, cioè:
ni
ni
Pi = X i * Pi dove X i =
= frazione molare
=
∑ n j n 1 + n 2 + ...+ n n
lim
p→0
La pressione parziale di un componente può essere anche espressa in termini di concentrazione molare, cioè il n° di moli di ciascun componente in un litro. In questo modo la pressione parziale diventa:
n
Pi = i ℜT = c i ℜT
V
Le proprietà di un gas ideale sono interpretate dalla teoria cinetica. Consideriamo le molecole come sfere rigide: esse deviano
dal loro moto rettilineo ed uniforme solo quando entrano in collisione fra loro o quando urtano le pareti del recipiente, cioè
quando avviene un urto anelastico che determina una variazione dell'energia cinetica di ognuna e quindi la loro velocità e di
conseguenza la loro quantità di moto, che ha come effetto macroscopico la pressione del gas. A temperatura costante si rag61
giunge uno stato stazionario in cui resta costante il numero di molecole che hanno una determinata velocità (in generale dipendente dal tempo) ed essa varia secondo la legge di distribuzione delle velocità molecolari di Maxwell:
3
mv
2
 m  2 − 2 kT
2
dM v = M * 4π * 
* v * dv
 *e
 2πkT 
dove dMv è il numero di molecole che hanno velocità comprese tra σ e σ+dv, M è il numero totale delle molecole, m la massa
molecolare, k=ℜ/N è la costante di Boltzman e T la temperatura assoluta.
La funzione dMv/dv definisce come varia il numero di molecola che hanno una certa velocità variando la velocità considerata. Essendo del tipo f(x)=a*x2*e-x2 quantitativamente sarà descritta dalla curva in figura. L'area totale sotto la curva rappresenta il numero totale di molecole M, l'area sotto la curva delimitata dagli estremi v
e v+dv è il numero di molecole la cui velocità è compresa tra questi due valori. Il
massimo della curva definisce la velocità più probabile ed esso, ottenuto derivando
la funzione precedente, è dato da:
1
v MAX
 2kT  2
=

 m 
La velocità media, un po' maggiore di quella probabile, è data da:
1
 8kT  2
2
v=
v MAX
 =
 π*m 
π
La velocità quadratica media è data da:
1
v=
 3kT  2
v =
 =
 m 
Le tre velocità stanno tra loro in rapporto v MAX : v: v = 1:
2
:
3
2
* v MAX =
3π
v
8
3
.
π 2
Aumentando la temperatura, la curva di distribuzione delle velocità molecolari si sposta verso destra e si appiattisce in quanto
aumenta il numero di molecole che hanno velocità elevate e diminuisce quello con velocità basse. In ogni caso l'area racchiusa
dalla curva resta costante, corrispondendo al numero totale di molecole data da:
1
3
2
E Trasl = mv = kT
2
2
che dipende dalla sola temperatura a cui è proporzionale. Inoltre essendo il moto di traslazione scomponibile lungo i tre assi x,
y, z ed essendo le tre direzioni del tutto equivalenti, si avrà che:
1
E Trasl x = E Trasl y = E Trasl z = kT
2
cioè l'energia cinetica media si equipartisce fra le tre componenti del moto di traslazione secondo le direzioni x, y, z in quantità
uguale pari a ½ kT per ogni componente. Tale risultato va sotto il nome di principio dell'equipartizione dell'energia. L'equazione di stato dei gas reali è data dallo sviluppo del viriale secondo le potenze di P, cioè pVm=A+BP+CP2+DP3+... dove i coefficienti del viriale sono funzioni della temperatura e dipendono dalla natura del gas. Raccogliendo A e ponendo B/A=B',
C/A=C' eccetera, si otterrà:
pVm=ℜT*( 1 + B'P + C'P2 + ...)
Si ha poi un altro sviluppo del viriale secondo le potenze di 1/Vm:

β
γ
β'
γ' 

+
+ ... = ℜT *  1 +
+
pVm = α +

2
Vm Vm
Vm Vm 2 

Indicando con Z (fattore di comprimibilità) l'espressione tra parentesi dei due sviluppi del viriale, si ha:
pVm = Z * ℜ * T
(
) (
) (
)
Lo stato solido
Abbiamo detto che nello stato solido la costituzione delle particelle realizza il massimo ordine. Per questo motivo le caratteristiche principali dei solidi cristallini sono la incomprimibilità, la rigidità e la regolarità della forma geometrica. Essi poi sono
anisotropi, cioè le loro proprietà fisiche variano in funzione della direzione lungo la quale vengono studiate. Un'altra caratteristica dei solidi cristallini è il loro punto di fusione ben definito: quando essi vengono riscaldati, conservano la loro struttura regolare fino ad una determinata temperatura, al raggiungimento della quale si verifica il collasso dell'edificio cristallino ed il
passaggio allo stato liquido. Per quanto riguarda la regolarità della forma geometrica, essa è limitata da facce piane ben definite
che formano tra loro angoli ben definiti. Poiché le facce esterne corrispondono a piani atomici del reticolo cristallino, che non
varia per una data specie, pur variando le forme esteriori, gli angoli diedri tra le facce corrispondenti non cambiano ( legge del62
la costanza degli angoli diedri di Berenguccio da Siena, 1540). Spesso le sostanze solide si presentano sotto forma di polveri i
cui granuli hanno struttura cristallina. Essi allora vengono detti solidi policristallini. Le dimensioni e la forma dei cristalli di
una data sostanza dipendono dalle condizioni in cui si forma il cristallo: una cristallizzazione lenta porta a cristalli grossi, mentre una precipitazione porta a cristalli piccoli. La classificazione dei solidi cristallini è basata sui diversi tipi di legame che le
particelle del reticolo, interagendo tra loro, realizzano. I solidi ionici e covalenti sono quelli caratterizzati dai più alti valori dell'energia di coesione e quindi queste sono sostanze poco volatili e con punti di fusione molto alti. I cristalli a struttura molecolare sono invece caratterizzati dai valori più bassi dell'energia di coesione e sono molto volatili, fondendo a basse temperature.
Per i cristalli metallici, l'energia di coesione varia entro intervalli molto ampi. La disposizione ordinata delle particelle in un
solido cristallino realizza la costruzione di un reticolo spaziale a periodicità regolare in tutte le direzioni. L'unità più piccola del
reticolo, la quale, ripetuta più volte nelle tre dimensioni, genera il cristallo, si chiama cella elementare. I vertici delle celle elementari sono i nodi del reticolo, occupati da atomi uguali. Bravais ha dimostrato che tutti i reticoli cristallini si possono ricondurre a 14 tipi fondamentali detti reticoli di Bravais, raggruppabili in 7 gruppi o sistemi cristallografici. Ogni cristallo inoltre
presenta sempre nel suo reticolo un certo numero di difetti che influisce sulle proprietà macroscopiche (meccaniche, elettriche
ed ottiche). Tali difetti si possono classificare in difetti puntiformi se riguardano qualche isolata posizione del reticolo, in difetti
lineari o dislocazioni se dovuti a piani del reticolo disposti irregolarmente o in difetti superficiali se si riferiscono ad imperfezioni sulla superficie esterna del cristallo. Prendendo in esame i difetti puntiformi, essi si possono presentare nel reticolo di un
cristallo formato da una sola specie di atomi o da molecole. Se in una posizione che dovrebbe essere occupata, manca un atomo
si ha una lacuna o vacanza. Un atomo fuori posto in una cavità posta tra altri atomi costituisce un difetto autointerstiziale.
Quando in un reticolo sono presenti atomi estranei si parla di impurezze sostituzionali se essi sostituiscono atomi del reticolo
nelle proprie posizioni, mentre si parla di impurezze interstiziali se essi si incuneano fra atomi del reticolo in posizioni irregolari. Le leghe sono sistemi formati da una o più fasi solide a più componenti, dei quali almeno uno è un metallo. Esse sono costituite da un metallo base e da uno o più elementi aggiunti in varia percentuale. Le leghe a due componenti vengono anche dette
leghe binarie. Si ha poi la distribuzione tra soluzioni solide primarie, che conservano la struttura reticolare di uno dei due componenti e le fasi intermedie che sono caratterizzate da una struttura diversa da quella di entrambi. Le soluzioni solide poi possono essere sostituzionali o interstiziali. Si ha una soluzione solida sostituzionale quando nel reticolo del metallo base MB un
certo numero di atomi è costituito da atomi dell'elemento aggiunto MA, che ne prendono il posto senza apportare variazioni
strutturali di rilievo, anche se si hanno distorsioni della cella elementare. Il metallo base funge da solvente mentre il metallo o
l'elemento aggiunto funge da soluto. La solubilità di MA è inversamente proporzionale all'entità della distorsione che esso provoca nel reticolo ospitante, quindi se essa è molto grande, MA è poco solubile in MB. La condizione dimensionale affinché due
metalli siano solubili l'uno nell'altro, allo stato solido ed in qualunque concentrazione, è che i loro raggi atomici rA ed rB non
differiscano per più del 15%. La solubilità è anche condizionata dalle loro strutture elettroniche, perché solo con strutture elettroniche simili i due metalli possono formare legami. Inoltre metalli con strutture regolari simili sono più solubili di metalli con
strutture reticolari diverse. Quindi la solubilità dipende dalle dimensioni atomiche della struttura elettronica e dalla struttura del
reticolo cristallino. Se questi fattori sono favorevoli si ha una solubilità completa. A volte si forma una superstruttura in cui gli
atomi del metallo aggiunto occupano nel reticolo del metallo base delle definite posizioni regolarmente disposte come nel caso
dell'ottone. Le soluzioni solide interstiziali si formano per inserzione di atomi di piccole dimensioni (come idrogeno, boro o
azoto) negli interstizi di un reticolo cristallino di un metallo.
Lo stato liquido
I liquidi costituiscono lo stato della materia intermedio fra quello gassoso e quello solido. Nei liquidi l'energia dei moti termici
è confrontabile con quella delle forze coesive e da ciò risulta una limitata libertà di movimento delle molecole che determina
una struttura disordinata nel suo insieme pur conservando un certo grado di ordine in regioni ristrette. Il disordine strutturale
determina l'isotropia delle proprietà dei liquidi, la loro tipica fluidità e la facile, reciproca diffusione tra liquidi diversi quando
siano portati in contatto l'uno con l'altro. Che le molecole di un liquido, pur essendo costrette a contatto tra loro, siano in movimento incessante è dimostrato dal fatto che se si sospendono in un liquido delle particelle di circa 10-4 cm. di diametro, esse
appaiono animate da un continuo e disordinato moto a zigzag, detto moto Browniano, che è la manifestazione diretta del movimento termico delle molecole di un liquido. A parità di temperatura, l'energia cinetica media e la frazione di molecole che
hanno un valore determinato di energia cinetica sono le stesse sia nello stato liquido sia in quello gassoso. Invece l'energia potenziale, determinata dalle interazioni intermolecolari, è più bassa per le molecole di un liquido che per quelle di un gas.
Pressione di vapore di un liquido
Se un liquido viene lasciato a sé in un recipiente aperto, evapora continuamente fino a trasformarsi tutto in vapore. Ciò è conseguenza della agitazione termica molecolare: tra le molecole alla superficie ce ne sono di quelle che hanno EC tale da poter
vincere le forze attrattive che tendono a tenerle prigioniere nella fase liquida, ed esse sfuggono nella fase vapore soprastante. Se
invece il recipiente è chiuso, il processo non prosegue indefinitamente, perché dopo un certo tempo, si giunge ad uno stato di
equilibrio tra i due processi opposti di evaporazione e di ricondensazione. In queste condizioni la concentrazione delle molecole nella fase vapore rimane costante, se costante viene mantenuta la temperatura. Perciò rimane costante anche la pressione esercitata dal vapore sulla superficie del liquido: essa è definita tensione di vapore o anche pressione di vapore. Aumentando la
63
temperatura la pressione di vapore aumenta perché un maggior numero di molecole passa dalla fase liquida alla fase vapore,
determinando un aumento di densità. Indicando con ve la velocità con cui le molecole evaporano alla temperatura T e con vc la
velocità con cui le molecole si condensano, la condizione di equilibrio è che ve=vc. Inoltre, essendo:
v e = c1 * e
−
∆E VAP
ℜT
vc = c2 * P
e
andando a sostituire alla condizione di equilibrio si ottiene:
c 2 * P = c1 * e
−
∆E VAP
ℜT
∆E
−
c 1 − ℜVAP
T
⇒ P = *e
= c*e
c2
∆E VAP
ln P = ln c −
ℜT
∆E VAP
ℜT
All'energia necessaria per vaporizzare una mole di liquido a pressione costante è dato il nome di calore latente molare di vaporizzazione LVAP, da cui, sostituendo:
P = c*e
−
L VAP
ℜT
La pressione di vapore cresce sempre col crescere di T. La temperatura alla quale il valore della pressione di vapore diventa
uguale a quello della pressione esterna è detta temperatura di ebollizione: si dice allora che il liquido bolle.
Soluzioni
Soluzione è un termine generico con cui si suole designare un qualunque sistema a più componenti fisicamente omogeneo, cioè
una qualsiasi fase in cui sono presenti più specie chimiche: esse sono costituite da un solvente liquido nel quale sono omogeneamente dispersi, allo stato molecolare o ionico, i soluti, che possono essere sostanze solide, liquide o gassose. La composizione
di una soluzione viene definita precisando le quantità relative dei componenti:
a) percentuali in peso = grammi del componente i per 100 g. di soluzione
% in peso del componente i =
gi
∑g
* 100
j
b) frazioni molari = rapporto fra il n° di moli del componente i e le moli totali
Xi =
ni
∑n
j
c) molarità o concentrazioni molari = n° di moli del soluto considerato al litro
ci =
ni
V
La molarità di una soluzione varia col variare della temperatura.
d) molalità = n° di moli di soluto in 1000 g. di solvente. Se in g0 grammi di solvente sono disciolte ni moli del soluto i:
mi =
ni
* 1000
g0
Se n0 è il numero di moli del solvente nella soluzione ed M0 è il suo peso molecolare, essendo g0 = n0 * M0:
mi =
ni 1000
*
n0 M 0
Per soluzioni molto diluite, molarità e molalità sono tra loro proporzionali e la costante di proporzionalità è la densità della soluzione, praticamente uguale a quella del solvente puro.
e) normalità = n° di grammo-equivalenti di soluto in 1 litro di soluzione
(ci)eq =
(n )
i eq
V
Solubilità
Riferendosi ad una data temperatura costante, si definisce solubilità di una sostanza in un determinato solvente la concentrazione massima che essa può raggiungere in quel solvente. Se il soluto è in eccesso oltre questa quantità limite, una parte di esso
resta indisciolta e si stabilisce uno stato di equilibrio tra soluto disciolto e non disciolto (equilibrio di solubilità). La soluzione
in queste condizioni è detta satura. A temperatura costante, la solubilità di un gas in un liquido aumenta con l’aumentare della
pressione.
64
Soluzioni ideali
La pressione di vapore di una soluzione, cioè la pressione della fase vapore con essa in equilibrio, è in genere una funzione
complessa della sua composizione, oltre che della temperatura. Vi sono però delle soluzioni per le quali la relazione tra pressione di vapore e composizione è molto semplice: sono le così dette soluzioni ideali, la cui formazione dal mescolamento dei
componenti puri non è accompagnata da alcun effetto termico. Ciò può verificarsi solo se i componenti della soluzione hanno
struttura molecolare molto simile. Per una soluzione ideale, la pressione parziale di vapore di ciascun componente è uguale alla
pressione di vapore del componente medesimo allo stato puro per la sua frazione molare nella soluzione (legge di Raoult):
Pi = Xi * Pi’
Una soluzione è detta ideale se i suoi componenti seguono questa relazione per qualunque valore della frazione molare.
Soluzioni non ideali
Le soluzioni che seguono la legge di Raoult per qualunque composizione sono relativamente poche: molte più sono quelle che
deviano. Per esse la dipendenza della pressione di vapore dalla composizione è spesso molto complessa.
1) se mescolando i componenti si ha sviluppo di calore
deviazioni negative
2) se mescolando i componenti si ha assorbimento di calore
deviazioni positive
Î
Î
Elettrolisi e processi agli elettrodi
I fenomeni che nelle soluzioni si accompagnano al passaggio di una corrente sono indicati col nome di elettrolisi. Sono dette
comunemente elettroliti quelle sostanze che in fase liquida, allo stato puro o in soluzione con solventi polari, sono dissociate in
ioni positivi e negativi liberi di muoversi sotto l’azione di un campo elettrico ed hanno perciò la proprietà di condurre la corrente elettrica per migrazione ionica.
L’elettrodo collegato al polo positivo della sorgente esterna è chiamato anodo e catodo quello collegato al polo negativo. Gli
ioni negativi che nella soluzione migrano verso l’anodo sono detti
anioni e quelli positivi che migrano verso il catodo sono detti cationi. L’intensità della corrente elettrica che attraversa la cella è apprezzabile solo se la differenza di potenziale applicata agli elettrodi supeConsideriamo,
dunque, una soluzione elettrolitica contenuta in una cella a
Elettroni
le continua.
I
Intensità di
corrente
Cationi
Potenziale di
decomposizione
Anioni
V
(d.d.p.)
ra un determinato valore di soglia, detto potenziale di
decomposizione. Giunti a questo valore, sulla superficie di separazione tra gli elettrodi e la soluzione si sviluppano delle reazioni chimiche. Questi processi agli elettrodi sono
l’aspetto più importante dell’elettrolisi. Esse sono determinate da un trasferimento di elettroni che si attua fra le specie ioniche
o molecolari presenti nella soluzione e gli elettrodi. Sul catodo (-) si ha un passaggio di elettroni dall’elettrodo, che ne è sovraccarico, agli ioni positivi contenuti nella soluzione, mentre l’anodo (+), che di elettroni è deficitario, li riceve dagli ioni negativi che lo circondano. Ogni processo che coinvolge il trasferimento di elettroni da una specie chimica ad un’altra è una ossidoriduzione: la specie che cede elettroni si ossida, mentre quella che li acquista si riduce. Il processo catodico è sempre una
riduzione di ioni o molecole della soluzione (e l’agente riduttore è l’elettrodo che dona elettroni alle specie che si riducono),
mentre il processo anodico è sempre un’ossidazione (e l’elettrodo fa da agente ossidante che sottrae elettroni alle specie che si
ossidano). I processi agli elettroni possono essere di diverso tipo, secondo:
1) la natura degli elettrodi. Si distingue tra elettrodi inerti, che agiscono semplicemente come trasportatori di elettroni, ed elettrodi reattivi, i quali partecipano direttamente alle reazioni che avvengono sulla loro superficie.
2) le specie presenti nelle soluzioni. Consideriamo separatamente i processi catodici ed anodici:
Sul catodo può compiersi la scarica di una catione MZ+:
65
Î
M
MZ+ + z eoppure una qualunque reazione di riduzione che assorba elettroni:
2 H2O + 2 eH2 + 2 OHContemporaneamente sull’anodo può attuarsi la scarica di un anione XZ-:
XZX + z ela dissoluzione dell’elettrodo stesso (se di materiale non inerte):
M
MZ+ + z eancora una qualunque reazione di ossidazione che liberi elettroni:
½ O 2 + 2 H + + 2 eH2O
La decomposizione elettrolitica è determinata dal passaggio della corrente attraverso la soluzione ed è quindi logico che la
quantità di elettrolita decomposto debba dipendere dalla quantità di elettricità trasportata attraverso la cella. Da queste considerazioni nascono le leggi di Faraday:
1) I legge di Faraday: la quantità di elettrolita decomposto, e quindi anche la quantità di specie formate agli elettrodi durante
l’elettrolisi, sono proporzionali alla quantità di elettricità che ha attraversato la cella, secondo l’equazione:
g=E*I*t
g=E*q
dove g è la quantità in grammi di elettrolita decomposto, I è l’intensità di corrente ed E è detto equivalente elettrochimico (è
una costante di proporzionalità).
2) II legge di Faraday: quantità eguali di elettricità decompongono elettrodi diversi in quantità proporzionali ai loro pesi equivalenti, secondo la formula: 1 F = NA * e = 96500 C, dove F è una grandezza chiamata Faraday, NA è il numero di Avogadro, e è la carica elementare. Il numero di equivalenti di una qualunque specie ionica scaricata ad un elettrodo è proporzionale alla quantità di elettricità che ha attraversato la cella. Se PF è il peso di formula di un dato ione e z la sua carica,
il suo peso equivalente è dato dalla formula:
Î
Î
Î
Î
Î
PF
z
Peq
Peq =
E=
=
PF
z*F
F
P
g = F *I *t
z*F
66
Dinamica chimica
Reazione chimica ed equazione stechiometrica
Ogni reazione è rappresentabile con un’equazione dove al primo membro sono indicati i reagenti iniziali ed al secondo membro i prodotti finali, entrambi accompagnati da opportuni coefficienti stechiometrici che precisano i rapporti quantitativi secondo cui, dai reagenti, si formano i prodotti. Una reazione può essere completa ed in questo caso irreversibile ( ), oppure parziale ed in questo caso reversibile ( ). Quando la conversione è parziale, cioè incompleta, si raggiunge una stato di equilibrio
nel quale sono presenti sia i reagenti che i prodotti in un rapporto quantitativo non più variabile nel tempo. Questo equilibrio
può essere spostato o verso i prodotti o verso i reagenti. Inoltre, per una qualunque reazione, deve valere la legge di Lavoisier,
cioè il principio di conservazione della massa e per quanto riguarda le reazioni ioniche, il principio di conservazione della
carica. Quindi, ogni equazione per soddisfare le due leggi, deve essere bilanciata con opportuni coefficienti stechiometrici. Le
reazioni poi si dividono in due gruppi:
1) reazioni che si verificano senza alcun trasferimento di elettroni fra gli atomi
2) reazioni in cui si ha trasferimento di elettroni da un atomo ad un altro.
Queste ultime vengono dette reazioni di ossidoriduzione o redox: esse sono la combinazione di un’ossidazione, cioè la trasforM, e di una riduzione, cioè la trasformazione
mazione di un atomo neutro in uno ione positivo secondo lo schema M+ + eM. L’atomo che acquista elettroni è un agente ossidante
di un atomo neutro in uno ione negativo secondo lo schema M- - e( e quindi si riduce ) e l’atomo che cede elettroni è un agente ossidante (e quindi si ossida). In generale si può dire che una reazione di ossidoriduzione è una reazione nella quale la trasformazione dei reagenti iniziali nei prodotti finali comporta qualche
variazione dei numeri di ossidazione dei componenti e l’elemento che si riduce diminuisce il proprio numero di ossidazione.
Per bilanciare una reazione di ossidoriduzione o si utilizza il metodo delle semireazioni o il metodo del trasferimento degli elettroni dagli atomi donatori a quelli accettori (cioè da quelli riducenti a quelli ossidanti). Si definisce reazione di autoossidazione o disproporziamento una reazione nella quale una stessa specie chimica agisce contemporaneamente da riducente e
da ossidante. Il significato quantitativo di una reazione chimica è data dal rapporto di reazione RR secondo il quale dai reagenti iniziali si formano i prodotti finali. Esso può essere espresso in molecole, in moli, in grammi (peso atomico degli elementi
che reagiscono e si combinano) o in litri.
Î
Ù
Î
Î
Redox
0
0
+1
−1
2 Na + Cl 2 → 2 Na Cl
1)
2)
3)
4)
5)
6)
7)
8)
Î
RR = 2:1:2
Un elemento libero (non combinato) ha n.o.=0
Tutti gli elementi del I gruppo hanno n.o.=+1
Tutti gli elementi del II gruppo hanno n.o.=+2
Tutti gli elementi del III gruppo hanno n.o.=+3
La somma algebrica di tutti i n.o. degli elementi di un composto deve essere sempre uguale a zero
Il numero complessivo degli elettroni ceduti deve essere uguale a quello degli elettroni acquistati
L’idrogeno in tutti i suoi composti ha n.o.=+1, ad eccezione degli idruri metallici in cui ha n.o.=-1
L’ossigeno in tutti i suoi composti ha n.o.=-2, ad eccezione dei perossidi in cui ha n.o.=-1 (un perossido è un ossido con un
atomo di ossigeno in più rispetto ad un normale ossido. I più comuni sono H2O2 (acqua ossigenata), Na2O2)
Redox in forma ionica
1)
2)
3)
4)
La somma algebrica dei n.o. di tutti gli elementi di uno ione complesso è uguale alla carica dello ione
Il n.o. di uno ione semplice è uguale alla sua carica
Per ogni atomo di O in più da una parte, si aggiunge una molecola di H2O dall’altra
Per ogni atomo di H in più, si aggiunge uno ione H+ dall’altra parte
Rendimento di una reazione
Il rendimento di una reazione è definita come il rapporto tra la quantità di prodotti ottenuta realmente e la quantità di prodotto
che ci si aspettava in teoria:
RESA% =
reale
* 100
teorica
67
Peso equivalente
Il peso equivalente di un composto è sempre una quantità riferita ad una data reazione. Il peso equivalente di un idrossido è uguale al rapporto tra il peso molecolare dell’idrossido ed il numero di gruppi OH che partecipano effettivamente ad una reazione. Il peso equivalente di un acido è uguale al rapporto tra il peso molecolare dell’acido ed il numero di H che partecipano effettivamente ad una reazione. Il peso equivalente di un sale è dato dal rapporto tra il suo peso molecolare ed il n.o. complessivo
del metallo che compare nel sale. Il peso equivalente di un composto che partecipa ad una redox è uguale al rapporto tra il suo
peso molecolare ed il numero di elettroni ceduti o acquistati dal composto nella reazione.
68
I fondamenti della termodinamica chimica
Definizioni e concetti generali: i sistemi termodinamici ed il loro stato
Si designa normalmente con la denominazione di sistema termodinamico ogni porzione dell’universo materiale che sia oggetto
di studio da un punto di vista termodinamico. Ambiente del sistema considerato è detto tutto il resto dell’universo che lo circonda. Un sistema si definisce chiuso se non si verificano scambi di materia con l’ambiente, mentre possono verificarsi scambi
di energia di qualunque tipo, sotto forma di calore o di lavoro. Si definisce aperto se possono verificarsi tra sistema ed ambiente sia scambi di materia che di energia. Si definisce isolato se è impedito ogni scambio di materia o di energia con l’ambiente.
La descrizione che la termodinamica ci fornisce di un qualunque sistema fa riferimento a proprietà definibili attraverso grandezze che sono il risultato medio macroscopico di un numero molto grande di fenomeni elementari concorrenti. La descrizione
termodinamica di un sistema richiede che siano specificate solo poche proprietà macroscopiche misurabili, il cui valore definisce completamente lo stato termodinamico del sistema considerato, in quanto determina univocamente anche quello d’ogni altra sua proprietà macroscopica. Le proprietà che definiscono in tal senso lo stato d’un sistema termodinamico sono correntemente chiamate variabili di stato. Quando il valore di qualche variabile di stato non rimane costante nel tempo, si dice che lo
stato del sistema varia, ossia che il sistema subisce una trasformazione: l’insieme degli stati intermedi attraverso cui il sistema
si evolve passando dallo stato iniziale a quello finale definisce il cammino della trasformazione. Facciamo ora alcune considerazioni sui gas ideali. Cos’è un gas ideale ? Di seguito sono elencate le sue caratteristiche:
1) dal punto di vista molecolare, le molecole del gas devono essere puntiformi rispetto alla distanza intermolecolare
2) non ci devono essere interazioni intermolecolari
È ovvio che il gas perfetto non esiste in natura. Per approssimazione si può però comparare il gas perfetto ad un gas molto rarefatto. Mentre un sistema meccanico, in genere è costituito da un solo oggetto, un sistema termodinamico può essere costituito
da numeri enormi di corpi (basti pensare che 1 mole di gas contiene 1NA = 6*1023 particelle).
Ogni particella del sistema termodinamico si muove, ma non liberadNV/dV
mente: segue la distribuzione di Maxwell-Boltzman. La temperatura è
direttamente proporzionale all’energia cinetica delle particelle, per cui
T1
T2 > T1 è un parametro che può caratterizzare lo stato termodinamico di un sistema. Un altro parametro è la pressione che diventa così un parametro
macroscopico conseguenza di fenomeni microscopici. Per un gas ideale
vale la relazione PV=nRT. Il terzo parametro è dato dalle concentraT2
zioni che esprimono la composizione chimica del sistema. Se le variazioni di stato (T, P, Ci) si modificano nel tempo, il sistema si trasforma, altrimenti permane in equilibrio termodinamico. Analizziamo ora
un altro concetto limite non presente in natura: la trasformazione reverV sibile. Consideriamo il sistema in figura.
Riscaldando il gas, questo tende ad espandersi ed il pistoP
P
ne si alza. Dunque il sistema subisce una perturbazione. Il
P1
P1
elemento 1
gas ideale si trasforma come indicato nel grafico PV. Ogni
elemento 2
punto del grafico rappresenta lo stato fisico di un certo
elemento 3
sistema. È importante notare che la temperatura è supposta
elemento 4
costante (si dice che la trasformazione è isoterma). Il tratto (p1,V1)-(p2,V2) del grafico è un arco di iperbole. RifeP2
P2
rendosi ora al secondo grafico si nota che se il pistone si
V1
V2
V
V1
V2
V
solleva, il gas si dilata prima nella sezione 4, poi nella 3,
nella 2 ed infine nella 1. Questo comporta valori diversi di
pressione nelle varie sezioni: il sistema, quindi, non è più
omogeneo. Raggruppando ora il sistema in una serie di
stati in cui la pressione è costante, si nota che se il pistone
1 si solleva velocemente, la banda delle curve sarà più larga
2 perché maggiori saranno le differenze di pressione fra le
3
varie sezioni. Se la velocità del pistone tende a zero (conV1
V2
4
cetto limite), il sistema è praticamente in equilibrio e
quindi la banda di curve si restringe. La trasformazione
viene detta reversibile. La trasformazione è reversibile anche per una variazione infinitesima di pressione, per cui il processo si
può invertire con una differenza di pressione o con una velocità infinitesima, ma opposta. In natura i processi non per lo più irreversibili. Una trasformazione è reversibile quando non solo si può ritornare allo stato di partenza (trasformazione invertibile),
ma anche quando tutto ciò che è entrato in contatto col sistema possa essere riportato allo stato iniziale.
69
Lavoro in una trasformazione termodinamica
Durante una trasformazione, un sistema può esigere un lavoro esterno, operando tramite qualche meccanismo sull’ambiente,
ovvero può eseguire l’esecuzione di un certo lavoro da parte dell’ambiente medesimo. Considerando le cose dal punto di vista
del sistema si assume positivo il lavoro eseguito sul sistema dall’ambiente e negativo quello eseguito dal sistema sull’ambiente,
perché nel primo caso il lavoro eseguito si traduce in un arricchimento d'energia da parte del sistema e nel secondo in una perdita d'energia da parte dello stesso. Consideriamo ora il lavoro in una trasformazione termodinamica. In queste trasformazioni
si parla di lavoro dinamico (meccanico). Sono più rari, ma in ogni modo esistono, i lavori elettrici e magnetici. Sappiamo che
δW = p * A * dx. Essendo A * dx = dV, si ricaW=F x S. Vediamo il caso di un pistone. Se A è l’area di base del cilindro
va che δW = -p * dV, in quanto il lavoro ha segno opposto alla variazione di volume. Quindi:
Î
W = −∫
Vf
Vi
Considerando una isoterma
Î pV = RT = cost. Î W = − ∫
p * dV
p * dV = − ∫ RT
Vf
Vf
Vi
Vi
Vf
dV
= − RT * ln
V
Vi
Chiamiamo funzione di stato un’equazione che descrive lo stato del sistema e che dipende solo dallo stato iniziale e finale. Noi
usiamo il δ quando ci riferiamo a quantità infinitesime e non a funzioni di stato. È importante osservare che il lavoro compiuto
o subìto da un sistema che passi da uno stato iniziale i ad uno finale f non dipende solo da questi stati estremi della trasformazione, ma anche dagli stati intermedi, cioè dal tipo di trasformazione considerata. Trasformazioni particolarmente importanti
sono quelle in cui lo stato iniziale coincide con quello finale (cicli). Vediamo ora brevemente il lavoro elettrico. Consideriamo
un accumulatore a piombo: i due processi di carica e scarica sono trasformazioni accompagnate dall’esecuzione di lavoro elettrico in quanto si ha il trasferimento di elettricità sotto l’azione di una differenza di potenziale. Questo lavoro è dato dal prodotto della quantità di elettricità trasportata per la differenza di potenziale. Inoltre il lavoro di scarica è negativo (cioè compiuto
sull’esterno) mentre quello di carica è positivo (cioè compiuto sul sistema). Tuttavia, essendo la d.d.p. pari alla forza elettromotrice ε, si avrà:
δW = ε * dq → W =
∫
qf
W =
∫
f
qi
i
ε * dq ed essendo dq = I * dt
ε * I * dt
Le proprietà macroscopiche di un sistema si dividono in proprietà estensive che dipendono dalla quantità di materia da cui il
sistema è formato ed in proprietà intensive che ne sono indipendenti. Sono proprietà estensive la massa, il volume ed il calore,
mentre sono proprietà intensive la temperatura, la pressione, la densità e la viscosità.
Energia interna di un sistema termodinamico
Prendiamo un sistema puramente meccanico, ad esempio un pendolo che oscilla nel vuoto senza attrito. Dato che ETOT = ECIN
+ EPOT , nell’oscillazione ci sarà un continuo passaggio da energia cinetica ad energia potenziale e viceversa. Se nel sistema
immetto aria, per attrito l’energia meccanica tende a dissiparsi in energia termica (calore). Con l’aria il sistema diventa termodinamico. Portando a contatto due corpi A e B a temperatura diversa, avviene un flusso di calore. La temperatura TA è legata
all’energia cinetica media delle molecole di A. Sull’interfaccia, le molecole di A urtano quelle di B e trasferiscono la loro energia cinetica di traslazione. Si tratta di un trasferimento molto disordinato. Noi chiamiamo calore il flusso di energia cinetica (o
di altre energie) da A o B. Si dice che il calore è una forma di energia ad alto contenuto di disordine. Si può convertire
completamente un’energia in calore, ma non si può fare l’inverso. Consideriamo ora un gas ideale. Per esso vale:
∆E = EEL + N*ETRASL = EEL + 3/2 N *K * T
dove N è il numero di molecole del gas. Se il gas non può essere considerato ideale, è necessario considerare, oltre all’energia
elettronica e di traslazione, anche l’energia potenziale derivante dalle interazioni intermolecolari (Van der Waals), quindi
l’espressione diventa:
∆E = EEL + EINT + 3/2 R * T
Tuttavia è da considerare che per un insieme di molecole monoatomiche si ha, oltre al moto di traslazione, anche un moto di
rotazione attorno al proprio baricentro ed un moto di vibrazione dei suoi atomi attorno alle posizioni di equilibrio.
∆E = EEL + ETRASL + EROT + EVIBR
È da notare che, se il sistema termodinamico è un liquido, concorrono alla sua energia anche i termini di energia potenziale relativi alle interazioni tra molecole. Per un solido cristallino, invece, bisogna considerare anche le vibrazioni reticolari degli asi hanno 3 gradi di libertà. Tuttavia il
tomi. Considerando un gas con molecole biatomiche ETRASL = 3/2 RT (per mole)
calcolo statistico, tenendo conto degli stati vibrazionali eccitati, porta a concludere che l’energia vibrazionale è data da:
Î
hν
EVIBR = N
e
hν
kT
−1
+ E0,VIBR
Raccogliendo poi in E0 l’energia elettronica e l’energia vibrazionale al punto zero, per una mole si ha che:
70
∆E = E0 +
3
RT + RT + N
2
hν
e
hν
kT
−1
L’ultimo elemento, a temperature molto alte, tende a RT, da cui si ha:
∆E = E0 + 3/2 RT + RT + RT = E0 + 7/2 RT
Il calore come forma di energia: l’equivalenza tra calore ed energia meccanica
La base su cui si appoggia la formulazione del I principio della termodinamica è la constatazione sperimentale dell’equivalenza
tra calore e lavoro meccanico.
Moto turbolento di una definita massa d’acqua
aumento della temperatura dell’acqua.
Joule si accorse, eseguendo questa esperienza, che rimaneva costante il rapporto W/Q. Questo
risultato è noto come principio dell’equivalenza tra calore e lavoro e la costante derivante dal
rapporto W/Q = J si dice equivalenza meccanico della caloria.
1 caloria = 4,184 joule
Î
La formulazione del primo principio della termodinamica
Il calore ed il lavoro sono quindi da considerare manifestazioni macroscopiche diverse di un’unica entità fisica, di quell’entità
che designiamo col termine molto generale di energia. Il primo principio della termodinamica, che è il principio della conservazione dell’energia, si può allora esprimere dicendo che la variazione, positiva o negativa, dell’energia di un qualunque sistema chiuso, durante una trasformazione, è uguale all’energia di qualsiasi tipo che il sistema riceve dall’ambiente circostante o
che ad esso cede. Se il sistema è isolato la sua energia rimane costante. In questa formulazione, parlando di sistemi termodinamici, il termine generico di energia designa l’energia interna del sistema considerato. Essa dipende solo dallo stato in cui il sistema si trova: è quindi una funzione di stato. Quando un sistema compie un lavoro sull’ambiente o ad esso cede calore, la sua
energia interna diminuisce (∆E<0), quando invece è l’ambiente che compie lavoro sul sistema o gli trasmette calore, la sua energia interna aumenta (∆E>0).
∆E = Q + W
Per convenzione, si assumono positivi il calore che entra nel sistema ed il lavoro compiuto sul sistema e negativi il calore che
esce dal sistema ed il lavoro da questo compiuto. In forma differenziale si indica dE = δQ + δW.
Entalpia
Il calore in gioco in una trasformazione dipende non solo dagli estremi di questa, ma anche dal percorso seguito dall’uno
all’altro, ossia dal tipo di trasformazione considerato.
a) volume costante
δQV = dE, ossia il calore in gioco in una trasformazione di questo genere è misurato dalla variazione
dell’energia interna del sistema.
b) pressione costante
δQP = dE + PdV = dE + d(PV) = d (E+PV).
La funzione di stato entro parentesi, E+PV, essendo una combinazione di funzioni di stato, è anch’essa una funzione di stato
che, indicata normalmente col simbolo H, è denominata entalpia del sistema:
H = E + PV
Il calore in gioco in una trasformazione a pressione costante è dunque misurato dalla variazione di entalpia del sistema. Confrontando i risultati ottenuti si ottiene:
QP = QV + P * ∆V
Queste conclusioni assumono un risultato molto importante quando la trasformazione considerata sia una reazione chimica, perché è su di esse che si basa il calcolo del calore di reazione.
Î
Î
Termochimica
Calore di reazione
Le reazioni chimiche sono accompagnate da sviluppo o assorbimento di calore e sono definite esotermiche nel primo caso ed
endotermiche nel secondo. L’effetto termico che si rende manifesto nello svolgersi di una reazione trae origine dal fatto che la
trasformazione dei reagenti nei prodotti implica un cambiamento di struttura molecolare, con contenuto energetico diverso.
L’effetto termico di reazione detto calore di reazione, dipende dalla natura dei reagenti e dei prodotti, dalla temperatura e dalle
condizioni in cui avviene la reazione ed è di regola definito supponendo i prodotti finali alla stessa temperatura dei reagenti ini71
ziali (reazioni isoterme). Se la reazione avviene a pressione costante, l’effetto termico è dato dalla variazione d'entalpia del sistema chimico considerato durante la reazione. Se la reazione avviene a volume costante, l’effetto termico è dato dalla variazione d'energia interna. Prendiamo una generica reazione:
lL + mM + ...
aA + bB + ...
indicando con Hi ed Ei rispettivamente l’entalpia e l’energia interna dell’i-esimo componente, il calore di reazione nei due casi
è:
QP = ∆H = ( lHL + mHM + ... ) - ( aHA + bHB + ... ) = Σ νi Hi
QV = ∆E = ( lEL + mEM + ... ) - ( aEA + bEB + ... ) = Σ νi Ei
avendo indicato con νi il coefficiente stechiometrico assunto col segno (+) per i prodotti e (-) per i reagenti. Poiché in genere le
reazioni avvengono a pressione costante, ci riferiremo a QP = ∆H = Σ νi Hi, detta entalpia di reazione.
Poiché ∆H = ∆E + p∆V e visto che p∆V è trascurabile rispetto a ∆E, essa è una misura approssimata della variazione di energia interna del sistema, che corrisponde all’energia dei legami e all’energia termica. Quindi, a temperatura costante, non è rilevante la variazione della parte termica, così che ∆H è essenzialmente associata alle variazioni strutturali che avvengono nel sistema, cioè alla rottura dei legami delle molecole primitive ed alla formazione dei legami nuovi: il calore di reazione è allora la
manifestazione macroscopica diretta di queste variazioni strutturali. Quando l’equazione stechiometrica di una reazione è scritta con l’indicazione del calore sviluppato o assorbito e delle condizioni di p e T a cui avviene, prende il nome di equazione
termochimica.
Î
Calore standard di reazione
Poiché l’effetto termico di una qualunque reazione varia al variare delle condizioni in cui è realizzata, la tabulazione dei dati
termochimici richiede la scelta, per ciascuna specie chimica, di uno stato convenzionale di riferimento (stato standard), così da
poter riportare l’effetto termico standard di ogni reazione. Il calore standard di reazione, riferendosi a condizioni di pressione e
temperatura costanti, è anche chiamato entalpia standard di reazione ∆H0. I dati delle entalpie standard sono in genere riportati
per una determinata temperatura ( 25°C ≡ 298 K ).
Calore standard di formazione
Î
Si definisce reazione di formazione di un composto la reazione nella quale il composto considerato prende origine dagli eleCH3OH reazione di formazione del metanolo). Quando si parla di reazioni
menti che lo costituiscono (es.: C + ½ O2 + 2 H2
di formazione, si considera sempre la formazione di una mole di composto ed il calore di formazione, che è l’effetto termico
che accompagna la reazione di formazione, è sempre intesa per una mole del composto stresso. Se gli elementi di partenza ed il
composto sono considerati nel loro stato standard, si parla di calore standard o di entalpia standard di formazione ( ∆H0Form ).
Il calore standard di formazione di un composto risulta definito dalla differenza tra l’entalpia standard di una mole del composto stesso e la somma delle entalpie standard degli elementi che lo formano, ognuna moltiplicata per il corrispondente coefficiente stechiometrico che compare nella equazione di formazione. Ponendo convenzionalmente uguale a zero l’entalpia standard di tutti gli elementi a qualsiasi temperatura, evidentemente l’entalpia standard di qualunque composto si identifica col suo
calore di formazione standard degli elementi costituenti alla temperatura considerata:
C (s,gr) + O2 (g)
CO2 (g)
∆H0Form = H0CO2 - ( H0C + H0O2 ) = H0CO2 - ( 0 + 0 ) = H0CO2
H0CO2 = ∆H0Form
Il calore standard di una reazione alla temperatura di riferimento (25°C), si calcola dalle entalpie standard dei soli composti:
CH4 (g) + 2 O2 (g)
CO2 (g) + 2 H2O (l)
∆H0 = ( H0CO2 + 2 H0H20 ) - ( H0CH4 + 2 H0O2 ) ponendo H0O2 = 0
Î
Î
Ù
Calore standard di combustione
L’effetto termico delle reazioni di combustione, detto calore di combustione, viene misurato bruciando una quantità nota della
sostanza studiata in una bomba calorimetrica a volume costante in atmosfera di ossigeno puro. Nella combustione di un composto organico formato da C, H ed O, i prodotti della combustione sono CO2 e H2O, ma l’acqua può essere allo stato di vapore o
allo stato liquido e deve essere riportato.
Calore latente di fusione, di vaporizzazione, di sublimazione
Con questi termini si indicano le quantità di calore che determinano la trasformazione in liquido di una mole di solido e la trasformazione in vapore di una mole di un liquido o di un solido alla temperatura di trasformazione che corrisponde alla temperatura considerata.
72
Calore di soluzione
Il calore o entalpia di soluzione di una sostanza è la quantità di calore sviluppata o assorbita quando una mole della stessa è
disciolta in una determinata quantità di solvente ad una definita temperatura e pressione: rappresenta perciò l’effetto termico
che accompagna la formazione di una soluzione contenente una mole della sostanza considerata (soluto) in un dato solvente
alla concentrazione precisata. Il calore di soluzione varia al variare della concentrazione della soluzione risultante, ossia, in ultima analisi, dalla quantità di solvente in cui è disciolta una mole del soluto: è conveniente esprimerla in moli. Il calore di soluzione cresce progressivamente, in valore assoluto, con l’aumentare della diluizione. Chiamo calore di diluizione la differenza
tra il calore di soluzione corrispondente alla concentrazione finale e quello corrispondente alla concentrazione iniziale.
Legge di Hess
In condizioni di pressione costante il calore di reazione è definito dalla variazione di entalpia: l’entalpia è una funzione di stato,
quindi in una reazione chimica la sua variazione dipende solo dallo stato iniziale e dallo stato finale del sistema considerato.
Pertanto in una reazione chimica l’effetto termico è indipendente dagli eventuali stadi intermedi attraverso i quali essa procede
e dipende soltanto dalla natura chimica e dalle condizioni fisiche dei reagenti iniziali e dei prodotti finali. Se, data una reazione,
si può formulare una sequenza di altre equazioni che permettano di riprodurre, per somma o differenza, l’equazione della reazione proposta, allora il calore di reazione di questa si ottiene sommando o sottraendo l’uno all’altro i calori di reazione delle
singole sotto-equazioni:
I
F
I
X, X
Y, Y
F
∆HI,F = ∆HI,X + ∆HX,Y + ∆HY,F
Î
Î
Î
Î
Equazione di Kirchoff
Definisce la dipendenza del calore di reazione a pressione costante dalla temperatura ed è definita come:
 ∂∆H 0 

 =
 ∂T  p
 ∂ H i0 
∑ ν i *  ∂T  = ∑ ν i c 0pi
p
dove c0pi è il calore molare a pressione costante del componenti i. Il calore molare è il calore specifico riferito ad una mole. Il
calore specifico ∂Q/∂T è la quantità di calore che serve a far alzare di 1°C un grammo di sostanza. C0p dipende dalla temperatura. Questa dipendenza si può approssimare come una somma di potenze della temperatura:
c0p = α1 + β1T + γ1T2 + ...
dove α, β, γ sono sempre più decrescenti e sono valori tipici di ogni sostanza. Comunque dall’equazione di Kirchoff:
 dH 0 

 = ∑ ν iα i + ∑ ν i βiT + ∑ ν iγ iT 2 + .. . = ∆α + ∆βT + ∆γT 2 + . ..
 dT  p
T
∫ d∆ H 0 = ∆ α
298 K
( ∆H )
0
T
T
∫ dT + ∆β
298 K
T
∫ T * dT + ∆γ
298 K
0
= ∆H 298
K + ∆ α (T − 298) +
T
∫T
2
* dT
298 K
∆β 2
∆γ
T − 298 2 ) +
(
(T 3 − 298 3 )
2
3
Se voglio passare da 25°C a X gradi, aggiungo a ∆H0298K i 3 termini successivi, conoscendo α, β, γ (dati sperimentali). Ad esempio considerando l’acqua:
α = 7, 2
0

 ∆H 298 K = − 57,8
−3
⇒
 β = 2, 3 * 10
0
 ∆H 373

K = − 57, 98
−6
γ = 0, 26 * 10
Il secondo principio della termodinamica
Abbiamo dedotto dal primo principio della termodinamica alcune considerazioni molto importanti sulle reazioni chimiche riguardanti in primo luogo il calcolo dei calori di reazione, ma non abbiamo potuto derivarne alcun criterio atto a prevedere, in
base alle proprietà individuali, caratteristiche delle singole specie chimiche, se in definite condizioni operative una data reazione può effettivamente compiersi, cioè se le specie chimiche che vorremmo fare reagire insieme per trasformarle in determinati
prodotti tendono spontaneamente, in queste condizioni, a reagire nel modo desiderato oppure no.
73
Supponiamo ora di avere un sistema nella situazione iniziale della figura. Se apriamo il rubinetto C, il gas fluisce liberamente da A a B finché le due pressioni si troveranno in equilibrio
(pA = pB). Ciò avviene spontaneamente ed irreversibilmente. L’espansione libera è tale
A
B
che la temperatura iniziale è uguale a quella finale. Perché il gas si espande liberamente ?
Potrebbe verificarsi spontaneamente il processo inverso ? In un sistema isolato se un processo è spontaneo e non c’è scambio di energia con l’esterno, allora tale processo è irreversibile
(a meno di interventi esterni). Ma perché il gas si espande se non c’è nessun vantaggio enerEspansione Libera
getico ? Diciamo intanto che l’esistenza di un sistema termodinamico è tanto più probabile
C
quanto aumenta il suo disordine interno. Si dice che il numero di microstati quantici aumenta con il disordine. Uno stato disordinato che ha a disposizione più microstati quantici è più
probabile di uno stato ordinato che ne ha meno. Il disordine aumenta con la temperatura
B
A
perché aumenta la possibilità di eccitarsi (distribuendo le particelle in più microstati quantici). Allo stato finale, quindi, concorrono due parametri: energia e disordine. In passato il
numero di microstati quantici è stato chiamato possibilità termodinamica. In realtà ciò non è
del tutto esatto: una probabilità è compresa tra 0 ed 1, per cui si preferisce parlare di molteplicità di microstati quantici. Più la
molteplicità è alta, più è probabile che si abbia quello stato. Dobbiamo concludere che il primo principio della termodinamica
non consente, da solo, di definire la direzione in cui spontaneamente si evolvono i processi chimici e fisici, ossia non fornisce
alcun criterio di spontaneità per le trasformazioni dei sistemi termodinamici in genere: questo criterio è fornito dal II° principio
della termodinamica. La molteplicità di microstati quantici dipende dalla libertà di movimento delle molecole e dalla loro probabilità di distribuirsi in un numero più o meno grande di stati quantici disponibili. Ecco perché essa cresce con l’aumentare
della temperatura, perché con questa aumenta rapidamente l’entità dei moti molecolari e s’incrementa il popolamento di un
maggior numero di stati quantici. All’aumento della temperatura diminuisce il peso del fattore energetico mentre aumenta quello del fattore probabilistico. In generale il fattore probabilistico è da ritenere favorevole per le reazioni nelle quali da agenti solidi o liquidi si formano prodotti gassosi o nelle quali aumenta comunque il numero delle molecole allo stato gassoso e per le
reazioni in cui da molecole più complesse prendono origine molecole più semplici:
1) reazioni con effetto termico e fattore di probabilità entrambi favorevoli: sono reazioni esotermiche nelle quali aumenta
il numero di molecole allo stato gassoso (es.: combustione);
2) reazioni con effetto termico favorevole e fattore di probabilità sfavorevole: sono reazioni esotermiche che portano ad
una diminuzione del numero di molecole allo stato gassoso ed alla formazione di molecole meno semplici delle originarie (es.:
reazioni di sintesi dei composti
H2 (g) + ½ O2 (g)
H2O (g) );
3) reazioni con effetto termico sfavorevole e fattore di probabilità favorevole: sono reazioni endotermiche che portano ad
un aumento di molecole allo stato gassoso (es.: reazioni di dissociazione);
4) reazioni con fattore di probabilità trascurabile: sono reazioni nelle quali non si ha variazione del numero di molecole
CO2 (g)).
allo stato gassoso (es.: C (s) + O2 (g)
Il risultato essenziale del secondo principio della termodinamica è proprio la formulazione rigorosa del fattore probabilistico
che con l’energia determina la direzione delle trasformazioni termodinamiche e che da essa emerge quel criterio di spontaneità
per le trasformazioni stesse che il primo principio da solo non può fornire. A tale formulazione si perviene con la definizione di
una nuova fondamentale funzione di stato, l’entropia, direttamente legata alla molteplicità dei microstati quantici. Il secondo
principio si esprime con la formulazione di due enunciati logicamente equivalenti:
1) Enunciato di Kelvin: non è possibile realizzare alcuna trasformazione ciclica ( e quindi alcuna macchina operante ciclicamente ) che abbia come unico risultato la produzione di lavoro prelevando calore da una sola sorgente a definita temperatura (impossibilità del moto di 2° specie perpetuo).
2) Enunciato di Clausius: non è possibile realizzare alcuna trasformazione ciclica ( e quindi alcuna macchina che operi in un
ciclo ) che abbia come unico risultato il trasferimento di calore da un corpo a temperatura più bassa ad uno a temperatura
più alta. Per trasferire calore da una temperatura più bassa ad una più alta è necessario assorbire energia dall’esterno ed è in
questo modo che funziona qualunque impianto frigorifero.
C
Î
Î
Î
Rendimento della conversione di calore in lavoro: teorema di Carnot
L’enunciato di Kelvin sancisce che è impossibile trasformare tutto il calore in lavoro. Dunque il rendimento termico di una
macchina ciclica non può essere mai pari al 100% (generalmente è circa il 30-40%). Ecco quindi il problema del rendimento
della conversione in lavoro del calore assorbito dalla macchina. Si definisce rendimento η di una macchina termica in una trasformazione ciclica il rapporto fra il lavoro da essa prodotto (considerato in valore assoluto) e la quantità di calore assorbita
dalla sorgente di alimentazione. Poiché in un ciclo ∆E=0, allora sarà |W| = |Q1| - |Q2| dove T1>T2, quindi:
η=
W
Q1
=
Q1 − Q2
Q1
= 1−
Q2
Q1
da cui si osserva che in ogni caso il rendimento è minore di 1.
Dall’enunciato di Clausius discende un importante teorema, noto come teorema di Carnot: tutte le macchine operanti ciclicamente e reversibilmente fra le medesime temperature dei due serbatoi (quello caldo e quello freddo), coi quali scambiano calo74
re nel loro funzionamento, hanno lo stesso rendimento, qualunque sia la natura del sistema termodinamico su cui, caso per caso,
esse operano. Il rendimento, quindi, in condizioni di completa reversibilità è funzione solo delle temperature T1 e T2 dei due
serbatoi termici di alimentazione e di scarico. Una trasformazione ciclica particolarmente semplice è quella nota con il nome di
ciclo di Carnot: è costituita da quattro distinti processi reversibili: due adiabatiche reversibili e due isoterme. Una macchina
qualunque che operi in un ciclo di Carnot è detta macchina di Carnot: si tratta di un tipo di macchina ideale, perché capace di
operare in maniera completamente reversibile, cioè in condizioni che in pratica non sono realizzabili. Il suo rendimento è quindi maggiore di quello di ogni altra macchina reale ed è da considerare il limite massimo a cui una macchina reale può avvicinarsi nel suo funzionamento. Il rendimento della macchina di Carnot operante fra le temperature T1 e T2 è definito, in funzione
di queste, dall’espressione:
ηC =
T1 − T2
T
= 1− 2
T1
T1
Il teorema di Clausius e la formulazione del secondo principio della termodinamica: l’entropia
Considerando una macchina che operi secondo un ciclo di Carnot, dalle espressioni che ne definiscono il rendimento se ne deduce che:
1−
Q2
Q1
= 1−
T2
T1
⇒
Q2
Q1
Q1
Q2
=
⇒
−
=0
T2
T1
T1
T2
e quindi, ricordando che Q1 è una quantità positiva perché è calore che entra nel sistema, mentre Q2 è una quantità negativa
perché è calore che ne esce, risulta:
Q1 Q2
+
= 0 nel caso di ciclo reversibile
T1 T2
Se si considera invece una macchina che operi secondo un ciclo non completamente reversibile, il rendimento della conversione del calore assorbito in lavoro risulta essere minore di quello proprio di una macchina di Carnot operante fra le stesse temperature e perciò si deduce:
1−
Q2
Q1
< 1−
T2
T1
⇒
Q2
Q1
Q1
Q2
Q Q
<
⇒0<
−
⇒ 1 + 2 < 0 nel caso di ciclo irreversibile
T2
T1
T1
T2
T1 T2
Î
Cerchiamo ora di estendere il concetto a cicli di qualunque tipo: consideriamo una generica trasformazione ciclica:
I° caso
reversibile: sezionando il ciclo con trasformazioni adiabatiche e congiungendo ognuna di queste con la successiva
mediante isoterme intersecanti il ciclo si ottiene una successione di n cicli di Carnot che nel loro insieme equivalgono, per n
molto grande, al ciclo originario. Il calore assorbito o ceduto dal sistema percorrendo la trasformazione ciclica considerata è la
somma delle quantità di calore assorbite o cedute lungo i tratti isotermi degli n cicli di Carnot (dato che lungo i tratti adiabatici,
per definizione, non si hanno scambi di calore) e che il lavoro ottenuto equivale alla somma dei lavori dei vari cicli di Carnot.
Quindi, indicato con Qi la quantità di calore scambiata lungo il tratto generico di isoterma alla temperatura Ti:
n
Qi
∑T
i =1
= 0 nel caso di ciclo reversibile
i
Se il numero di adiabatiche considerato è grande e queste sono infinitesime, lungo ogni tratto di isoterma sarà scambiata una
quantità infinitesima di calore pari a δQ, da cui:
∫
II° caso
δQREV
= 0 noto come integrale di Clausius
T
Î irreversibile: con analoghi ragionamenti si ottiene:
∫
δQIRR
<0
T
δQ REV
è il diffeT
renziale di una funzione di stato, ossia è un differenziale esatto, per cui si può porre la quantità stessa pari a dS. Alla funzione
di stato così introdotta in base al teorema di Clausius per una trasformazione completamente reversibile, è stato dato il nome di
entropia del sistema considerato:
Considerando una trasformazione ciclica completamente reversibile è immediato riconoscere che la quantità
f
∆S = S f − S i =
∫
i
δQREV
T
Considerando una trasformazione ciclica non completamente reversibile, si avrà:
75
δQIRR
δQIRR
dS >
⇔ ∆S > ∫
T
T
i
f
Il principio dell’incremento dell’entropia
In un sistema isolato, mentre per ogni trasformazione reversibile che vi si compia l’entropia resta costante, qualunque trasformazione irreversibile comporta un aumento dell’entropia (dS ≥ 0). Si consideri una generica trasformazione irreversibile: supponendo infinitesime le quantità di calore scambiate, così da poter ritenere costanti T1 e T0 (con T0 < T1), si ha:
• per il sistema:
• per l’ambiente:
da cui si ha:
δQ
T1
δQ
=+
T0
dS SIST = −
dS AMB
 1
1
dST = dS SIST + dS AMB = δQ −  > 0 . Così si ha un aumento di entropia nel complesso
 T0 T1 
sistema + ambiente, tanto più grande quanto più elevata è la differenza di temperatura T1 - T0, ossia quanto più ci si discosta
dalle condizioni di reversibilità. Da ciò discende il principio dell’incremento dell’entropia dell’universo. Infatti nell’universo,
che può essere considerato come il più grande sistema isolato esistente, le trasformazioni che vi si compiono sono tutte di tipo
irreversibile in quanto avvengono spontaneamente, per cui, per quanto detto sopra, l’entropia aumenta di valore. Da notare con
non si possono avere trasformazioni che facciano diminuire l’entropia, in quanto dS ≥ 0. Ora vediamo come fare a calcolare
dSSIST e dSAMB:
dS =
δQP dH cP
=
=
dT
T
T
T
dove QP è il calore scambiato a pressione costante (condizione di ogni generica reazione chimica) e cP è il calore molare.
L’entropia assoluta è:
T
S=
∫
0
cP
dT + S0
T
dove S0 rappresenta l’entropia della specie considerata allo zero assoluto. Riferendoci al caso dell’azoto, il calcolo
dell’entropia a 25°C ≡ 298 K ed alla pressione di 1 atm. Si imposta secondo lo schema seguente:
TTIPO − i , ii
S1atm =
∫
0
(c )
p
T
s,I
( )
( )
( )
TFUS
TEBOL c
298 K c
cp
p
∆HTIPO− I , II
p
∆H FUS
∆HVAP
s , II
l
dT +
+ ∫
dT +
+ ∫
dT +
+ ∫
TTIPO− I , II
T
TFUS
T
TEBOL TEBOL T
TTIPO − i , ii
TFUS
g
dT
dove TTIPO-I,II è la temperatura alla quale l’azoto passa da solido cristallino di un tipo a solido cristallino di altro tipo, TFUS è la
temperatura alla quale l’azoto fonde, TEBOL è la temperatura alla quale l’azoto liquido vaporizza. I valori delle altre grandezze,
come si vede dai nomi, vengono presi alle temperature indicate (es.: ∆HFUS è il valore che l’entalpia assume alla temperatura di
fusione dell’azoto). In pratica per calcolare S1atm vengono sommati tutte le sotto-entropie che si incontrano andando dallo zero
assoluto all temperatura desiderata. Questo perché, durante i cambiamenti di stato fisico del sistema (solido liquido vapore), il calore specifico cambia il suo modo di evolversi in funzione della temperatura (e quindi anche
l’entropia perché viene calcolata da esso).
Î
Î
Entropia e probabilità termodinamica di stato
Ogni sistema termodinamico isolato tende ad evolversi spontaneamente verso lo stato più probabile, quindi ogni processo spontaneo non è che una trasformazione del sistema in cui il processo considerato si svolge da uno stato di minore probabilità ad
uno di probabilità maggiore. Siccome ogni processo spontaneo in un sistema isolato è accompagnato da un incremento
dell’entropia, è naturale che esista una stretta relazione fra l’entropia di un sistema e la probabilità termodinamica dello stato in
cui esso si trova. Dicendo P la probabilità di un determinato stato, si può indicare che l’entropia S è funzione di P ( S = ƒ(P) ).
S AB = S A + S B = f ( PAB ) = f ( PA * PB )
 f ( PA ) + f ( PB ) = f ( PA * PB )
S A = f ( PA ) ∧ S B = f ( PB )

La relazione funzionale dunque deve essere di tipo logaritmico. Essa è precisata dalla equazione di Boltzmann-Plank che esprime la definizione statistica dell’entropia: S = k* ln P.
76
Il terzo principio della termodinamica e l’entropia allo zero assoluto
Ogni specie chimica ha un’entropia che è finita e positiva, che è una funzione crescente con la temperatura e che col tendere
della temperatura allo zero assoluto tende ad un valore costante, indipendente dalla pressione, dallo stato di aggregazione, dalla
forma allotropica o dalla forma cristallina, valore che diventa zero nel caso di sostanze cristalline che siano cristalli perfetti. Un
cristallo perfetto è una sostanza cristallina la cui struttura microscopica reticolare può realizzarsi solo secondo un unico modello, cioè secondo un solo tipo di distribuzione dei suoi atomi o delle sue molecole o dei suoi ioni, senza irregolarità alcuna. Il
numero di microstati quantici è pari ad 1 (in quanto, come già detto, esiste un unico modello per la disposizione degli atomi del
reticolo), quindi la probabilità P che gli atomi si dispongano in quella determinata maniera è pari alla certezza, cioè P=1
S=
k * ln 1 = 0 (entropia nulla). Se invece il cristallo non fosse perfetto, i microstati quantici sarebbero più di uno, quindi la probabilità (per ognuno di essi) sarebbe minore di 1 (la loro somma sarebbe, ovviamente pari ad 1) e quindi S > 0. Il terzo principio della termodinamica sancisce anche l’impossibilità di raggiungere lo zero assoluto con un numero finito di trasformazioni.
Î
Energia libera
Il criterio di spontaneità per le trasformazioni che avvengono in un sistema isolato è espresso dalla condizione dS > 0 mentre lo
stato di equilibrio è determinato dalla condizione dS = 0. È però da osservare che raramente la termodinamica chimica considera sistemi isolati. Supponiamo che sistema ed ambiente siano in equilibrio termico alla temperatura T e che temperatura e pressione restino costanti nel sistema durante la trasformazione che si considera. Essendo il sistema sempre in equilibrio termico
con l’ambiente, ogni scambio di calore tra loro è reversibile, quindi il calore perduto dal sistema è guadagnato dall’ambiente e
viceversa, cioè δQAMB = - δQSIST , per ogni trasformazione infinitesima che avviene nell’insieme
sistema + ambiente: dSTOT = dSAMB + dSSIST ≥ 0 e siccome l’entropia dell’ambiente varia per effetto del calore scambiato con
il sistema reversibilmente:
dS AMB =
δ QAMB
δQ
= − SIST
T
T
e quindi
dS SIST −
δ QSIST
≥0
T
Per il primo principio dESIST = δW + δQSIST e se il lavoro è solo di espansione o di contrazione, essendo δW = -p dVSIST, otteδQSIST = dESIST + p dVSIST. Sostituendo nella precedente:
niamo: δQSIST - p dVSIST = dESIST
Î
dS SIST −
dESIST + pdVSIST
≥0
T
ovvero
d( ESIST + p VSIST - T SSIST )T,p ≤ 0
T * dSSIST - dESIST + p dVSIST ≥ 0
Questo se temperatura e pressione sono costanti. L’espressione entro parentesi è una funzione di stato del solo sistema, in quanto è una somma di funzioni di stato di questo: è designata col nome di energia libera di Gibbs (o anche solo energia libera) ed è
indicata col simbolo G. Indicando H = E + pV otteniamo G = ( E + pV ) - T S = H - T S, per cui l’espressione differenziale
diventa ( dGSIST )T,p ≤ 0. Questa diseguaglianza non è di validità generale, ma si applica solo ai sistemi termodinamici per i
quali si abbia da considerare esclusivamente lavoro meccanico di espansione o di contrazione (ossia derivante da eventuali variazioni di volume), con esclusione quindi di altre forme di lavoro ed in condizioni di temperatura e pressione costanti. La formula esprime il fatto che in qualunque sistema che si trovi in definite condizioni di temperatura e pressione, ogni trasformazione spontanea è accompagnata da una diminuzione della sua energia libera e non possono verificarsi spontaneamente trasformazioni che compiano una aumento di essa. Se poi dG=0, essa ha il valore minimo possibile per il sistema considerato, che è inoltre in equilibrio termodinamico. Si noti che una diminuzione dell’energia libera del sistema corrisponde ad un aumento
dell’energia complessiva del sistema + ambiente.
Energia libera e lavoro utile
Sino ad ora abbiamo considerato esclusivamente il lavoro meccanico. Ora però è opportuno togliere questa limitazione per trarre conclusioni valide anche per altri tipi di lavoro. Non si deve considerare solo il lavoro meccanico δW, ma anche altre forme
di lavoro δW’, detto lavoro extrameccanico, in quanto non comporta variazione di volume del sistema. Allora δW’ è detto lavoro utile, cioè lavoro liberamente disponibile, mentre δW è detto lavoro sprecato perché non liberamente utilizzabile, ma solo
sfruttando la variazione di volume. Quindi δWT = -p dV + δW’. Il primo principio diventa quindi:
77
dESIST = δQSIST − pdVSIST + δW ′
δ QSIST = dESIST + pdVSIST − δW ′
dS SIST −
dESIST + pdVSIST − δ W ′
≥0
T
TdS SIST − (dESIST + pdVSIST ) + δW ′ ≥ 0
[
]
d (TS SIST )T , p − dESIST + d ( pVSIST )T , p + δW ′ ≥ 0
d (ESIST + pVSIST − TS SIST )T , p ≤ δW ′
(dG )
SIST T , p
≤ δW ′ ⇔ − (dGSIST )T , p ≥ −δW ′
Se ne conclude che quando in un sistema a temperatura e a pressione costanti si attua una trasformazione reversibile, il lavoro
utile compiuto dal sistema (cioè considerando l’espressione -(dGSIST)T,p ≥ -δW’) è uguale alla diminuzione della sua energia
libera, mentre quando avviene una trasformazione irreversibile detto lavoro è inferiore ad essa. La diminuzione di energia libera in una trasformazione a temperatura e pressione costanti segna il limite massimo del lavoro utile ottenibile dal sistema considerato: il lavoro utile risulterà ad essa uguale solo se la trasformazione è reversibile e minore ad essa se la trasformazione è irreversibile. Quindi il massimo di lavoro sfruttabile lo si ha in condizioni di reversibilità: ogni causa di irreversibilità determina
una minore disponibilità di lavoro utile in quanto sottrae irrimediabilmente dell’energia, così che se ne riduce la quantità convertibile in lavoro. È questo, in definitiva, il concetto di degradazione dell’energia che accompagna ogni trasformazione irreversibile.
78
Applicazioni chimiche dei risultati fondamentali del secondo principio della termodinamica
Condizioni termodinamiche di spontaneità di una reazione
Î
lL + mM + ... Se in determinate
Supponiamo di avere una certa reazione la cui equazione stechiometrica sia aA + bB + ...
condizioni di temperatura e pressione risulta essere ∆G < 0, allora la reazione avviene spontaneamente, se invece ∆G > 0, la
reazione non avviene spontaneamente nel senso voluto ( ), ma nel senso opposto ( ). Si consideri per esempio la decomposizione del carbonato di calcio CaCO3 (calcare) in CaO e CO2: CaCO3 (s)
CaO (s) + CO2 (g). A temperatura ambiente
(25°C) questa reazione è termodinamicamente impedita perché risulta ∆G > 0 (≈ 31 Kcal), ma a temperatura superiore agli
820°C il calcare si dissocia spontaneamente alla pressione atmosferica, perché dopo questa temperatura si ha ∆G < 0. Quando
in un sistema chimico chiuso avviene una reazione, la sua energia libera progressivamente diminuisce fino a che il sistema medesimo raggiunge lo stato di equilibrio relativo alle condizioni a cui è sottoposto: allora l’energia libera del sistema raggiunge il
valore minimo compatibile con quelle condizioni e risulta, come si è visto, dGT,p = 0. Come abbiamo già detto, ogni reazione è
governata dal gioco concomitante di un fattore energetico (l’effetto termico) e di un fattore di probabilità: ebbene questi due
fattori, insieme, definiscono proprio la diminuzione di energia libera che è la causa determinante dello svolgersi spontaneo di
una reazione. Quei due fattori nell’espressione della variazione di energia libera che la reazione comporta sono individualmente
ed esplicitamente precisati. Infatti per una reazione a pressione e temperatura costanti, si ha:
(∆G SIST)T,p = (∆HSIST)T,p - T (∆SSIST)T,p
espressione che mette in evidenza il fattore energetico, definito dalla variazione di entalpia del sistema, che esprime l’effetto
termica della reazione, ed il fattore di probabilità definito dalla variazione di entropia, che è legata alla diversa probabilità termodinamica dello stato finale e di quello iniziale ( ∆S = k ln [PF / PI] ) e quindi alla variazione del grado d’ordine e della libertà di movimento delle molecole in seguito alla reazione. Concludendo si può dire in generale che la spontaneità di una reazione
è controllata dal segno di ∆H e di ∆S secondo lo schema seguente:
1) ∆H < 0, ∆S > 0
la reazione può avvenire spontaneamente a qualunque temperatura, perché ∆G < 0 sempre;
2) ∆H > 0, ∆S < 0
la reazione non può mai avvenire spontaneamente, perché ∆G > 0 sempre;
Î
Î
Í
Î
Î
∆H
3) ∆H < 0, ∆S < 0 Î la reazione avviene solo a basse temperature, quando | T ∆S | < | ∆H |, cioè per T <
∆S
4) ∆H > 0, ∆S < 0
Î la reazione avviene solo ad alte temperature, quando | T ∆S | > | ∆H |, cioè per T > ∆∆HS
Indicando poi con Gi l’energia libera molare del componente i, si ha che:
∆G = (lGL + mG M + . . .) − (aG A + bGB + . . .) ⇒ ∆G =
∑ν G
i
i
Questa quantità che esprime la variazione di energia libera del sistema considerato quando il numero di moli di ciascun componente varia della quantità indicata dal rispettivo coefficiente stechiometrico, è chiamata energia libera di reazione. Anche per
le energie libere esistono valori standard G0i alla temperatura di 25°C. Così come per l’entalpia, essi sono definiti ponendo uguale a zero l’energia libera standard degli elementi, così che l’energia libera standard di un composto si identifica con la sua
energia libera standard di formazione dagli elementi. Questi valori sono convenzionali e non coincidono con i valori di G0 = H0
- TS0. Tuttavia si utilizzano le energie molari standard per calcolare l’energia libera standard di reazione:
∆G 0 =
∑ν G
i
0
i
quindi a noi interessano le variazioni di G piuttosto che i suoi valori assoluti. Il valore dell’energia libera di formazione di un
composto è l’indice della sua stabilità termodinamica. Se nel processo di formazione di un composto ∆G > 0 e quindi è termodinamicamente impedito, allora il composto è da considerarsi stabile nel senso che non tende a decomporsi negli elementi. Se
invece ∆G > 0 di formazione, allora il composto risulterebbe instabile. Ad ogni modo si tratta di una stabilità relativa. Per poter
definire un composto stabile in senso assoluto, deve risultare termodinamicamente impedita, oltre alla reazione di decomposizione negli elementi, ogni altra reazione di decomposizione del composto in prodotti diversi. Consideriamo la formazione
dell’ossido di azoto:
1
1
N 2 + O2 ⇒ NO
2
2
0
0
0
− T∆SNO
(∆G )NO = ∆H NO
dalle tavole otteniamo ∆H0NO = 21600 Cal/Mole. Per trovare l’entropia ed infine l’energia libera:
79
0
∆S NO
=
(
[
)
1 0
1
0
0
50, 34 − (45, 2 + 49,0) = 2,95 Cal Mole
S
−
S
+
S
=
NO
N
O
2
2
,
2
2
PRODOTTI
REAGENTI
TABELLE
[
0
= (∆G 0 ) NO = 21600 − 298 * 2.95 = +20700 Cal Mole
G NO
]
]
Poiché ∆G > 0 ( + 20700 ), la reazione avviene spontaneamente in senso opposto, per cui l’ossido di azoto (NO) è instabile.
KCl + 3/2 O2 è termodinamicamente favorita (∆G0 = -28,5 Cal/mole).
Invece la reazione KClO3
Î
Dipendenza dell’energia libera dalla temperatura e dalla pressione
Avendo detto che G = H - TS, vogliamo far vedere che essa dipende dalla temperatura e dalla pressione. Considerando una variazione infinitesima dG = dH - d( TS ) = d( E+pV ) - d( TS ) = dE + pdV + Vdp - TdS - SdT . Ma in una trasformazione reversibile, TdS = δQ = dE + pdV (considerando come unico lavoro quello meccanico di espansione e contrazione), da cui si ha:
dG = Vdp - SdT, quindi se si considera il sistema ad una determinata temperatura costante: (dG)T = Vdp. Questa è la base per
dedurre l’espressione dell’energia libera molare di una qualunque specie chimica ad una determinata temperatura in funzione
della pressione.
Reazione chimiche ed equilibrio
Î
lL + mM +... La
Si consideri un sistema chiuso, a temperatura e a pressione costanti e la generica reazione aA + bB + ...
composizione del sistema, dunque, va progressivamente variando, dapprima più rapidamente, poi mano a mano sempre meno,
finché dopo un periodo più o meno lungo di tempo, essa si conserva costante indefinitamente. Si dice allora che il sistema è in
equilibrio chimico ed in queste condizioni la sua composizione, ormai invariabile nel tempo, determina il rendimento massimo
col quale è possibile ottenere i prodotti nelle condizioni operative in cui la reazione è compiuta. Considerando il nostro sistema,
mentre si formano dnl moli di L, dnm moli di M in seguito alla reazione di dna moli di A, dnb moli di B, l’energia libera del
sistema subisce una variazione dG:
(dG )T , p = ∑ Gi dni = G AdnA + GB dnB + . ..+ GL dnL + GM dnM + .. .
Le variazioni dei numeri di moli dei diversi componenti ( dni ) sono legate tra loro dalla stechiometria della reazione, cioè sussiste una relazione di proporzionalità del tipo:
(− dn ):(− dn ):. . .: dn : dn
A
−
B
L
M
:. . . = a: b:. ..: l : m:. ..
dnA
dn
dn
dn
= − B = . . . = L = M = .. . = dξ
a
b
l
m
Cioè momento per momento è uguale per tutti i componenti il rapporto fra la variazione del numero di moli che la reazione determina ed il coefficiente stechiometrico del componente considerato. Ricordando che νi è positivo per i prodotti e negativo per
i reagenti: dni = νi dξ. La composizione del sistema risulta così definita istante per istante dal parametro ξ, detto grado di avanzamento della reazione, perché col proprio incremento ne esprime il graduale progredire.
∆ni = ν i ∆ξ ⇒ ∆nA = − a∆ξ . .. ∆nL = l∆ξ .. .
∆ξ = 1 ⇒ ∆nA = − a. . . ∆nL = l
Dunque ad un incremento unitario del grado di avanzamento corrisponde una variazione del numero di moli di ciascun componente uguale al suo proprio coefficiente stechiometrico. Sostituendo il risultato ottenuto otteniamo:
(dG )T , p = (lGL dξ + mGM dξ + . . .) − (aG Adξ + bGB dξ + . . .) = [(lG L + mGM + .. .) − (aG A + bGB + . . .)]dξ
Nel progressivo avanzamento della reazione dG varia da istante ad istante variando le energie libere molari dei componenti e
fintantoché dG < 0 la reazione può procedere spontaneamente.
 ∂G 
=


 ∂ξ  T , p
[(lG
L
]
+ mG M + . . .) − (aG A + bGB + . . .) = (∆G )T , p
che rappresenta la variazione di energia libera relativa alla trasformazione. Essa definisce l’energia libera di reazione che è la
variazione della energia libera del sistema che accompagna il decorso della reazione corrispondete ad un incremento unitario
del grado di avanzamento. Quando, dopo un certo periodo di tempo, dG=0 e quindi  ∂G  = (∆G ) = 0 , il sistema avrà
T,p
 ∂ξ  T , p
raggiunto le condizioni di equilibrio chimico e l’energia libera il suo valore minimo. Esprimendo ora in forma più generale, in
80
funzione dell’attività del componente, cioè ponendo Gi = G0i + RT ln ai, e ricordando che per i componenti allo stato standard
è (∆G0)T,p = (lG0L + mG0M + ...) - (aG0A + bG0B + ...), si ottiene:
(∆G )T , p = ∑ ν i Gi0 + RT (l * ln a L + m * ln a M + . . .− a * ln a A − b * ln a B − . . .) ⇒
 a Ll * a Mm *. .. 
 a Ll * a Mm *.. . 
0
⇒ ∑ ν i G + RT * ln a
 = (∆G )T + RT * ln a

 a A * a Bb *. .. 
 a A * a Bb *.. . 
0
i
Questa equazione è nota col nome di isoterma di reazione di Van’t Hoff in quanto fissa la direzione in cui, a temperatura e
pressione costanti, la reazione considerata procede spontaneamente. Quando la reazione giunge all’equilibrio:
(∆G )
0
T
 (a )l * (a )m *.. . 
M eq
 L eq

+ RT * ln
a
b
 =0
*
*.
.
.
a
a
(
)
(
)
A
B


eq
eq
dove (ai)eq indica l’attività del componente i all’equilibrio, si ottiene:
 (a )l * (a )m *. . . 
M eq
∆G 0
 L eq

ln
a
b
 = − RT
*
*.
.
.
a
a
(
)
(
)
A
B


eq
eq
il cui secondo membro è indipendente dalla composizione del sistema, ma dipende solo dalla temperatura. Dunque il primo
membro, per T costante, è un’invariante della reazione studiata:
 (a )l * (a )m *. . . 
M eq
 L eq

ln
a
b
 = ln K
*
*.
.
.
a
a
(
)
(
)
A
B


eq
eq
(a ) * (a )
K=
(a ) * (a )
l
m
L eq
a
M eq
b
A eq
B eq
*. . .
*. . .
dove K prende il nome di costante di equilibrio della reazione considerata.
All’equilibrio, quindi si ha: ∆G° = -RT ln K.
Legge dell’equilibrio chimico
Ad equilibrio raggiunto il rapporto tra il prodotto delle attività della specie chimiche che nella reazione si formano ed il prodotto delle attività delle specie chimiche reagenti, elevate ciascuna ad una potenza corrispondente al proprio coefficiente stechiometrico, è, per una data reazione, invariante ed il suo valore dipende solo dalla temperatura (chiamata anche legge dell’azione
di massa). Introduciamo ora il quoziente di reazione:
a lL * a mM *...
Q= a
a A * a bB *...
da cui possiamo esprimere la isoterma di reazione in forma compatta:
∆G = − RT * ln K + RT * ln Q = RT * ln
Q
K
Considerando la generica reazione, in determinate condizioni di temperatura e pressione, essa può procedere spontaneamente
da sinistra a destra se è Q<K, per raggiungere l’equilibrio quando Q (che varia col grado di avanzamento) diviene eguale a K;
se invece fosse Q>K, in quelle condizioni tenderebbe ad avvenire spontaneamente la reazione opposta.
Reazioni termodinamiche favorite e non favorite: posizione dell’equilibrio
Anziché alle attività ci riferiremo ora alle concentrazioni, da cui:
c lL * c mM *...
∆G = ∆G°+ RT * ln a b
c A * c B *...
Supponiamo, come primo caso, che l’energia libera standard di reazione
∆G° = ∑ υ i G° i sia negativa: ∆G°<0.
La reazione si evolverà ulteriormente nel senso indicato finché ∆G°<0, ma mano a mano che essa procede, il rapporto tra le
concentrazioni dei prodotti (che aumentano) e quelle dei reagenti (che decrescono), rapporto ormai positivo, va gradualmente
81
c lL * c mM *...
aumentando e, con esso, aumenta RT * ln a
fino ad eguagliare in valore assoluto ∆G°: quando ciò si verifica, si
c A * c bB *...
realizzano le condizioni di equilibrio ed il rapporto delle concentrazioni diventa uguale alla costante di equilibrio della reazione
alla temperatura considerata. Il rapporto delle concentrazioni dei prodotti e dei reagenti all’equilibrio (che si identifica con la
costante di equilibrio della reazione) definisce quella che i chimici chiamano posizione dell’equilibrio. Si dice che l’equilibrio
di un sistema in reazione è più o meno spostato verso i prodotti finali o verso i reagenti iniziali a seconda del valore di detto
rapporto. Se dunque per una reazione vale ∆G°<0 e K>1, l’equilibrio è spostato verso i prodotti finali: una reazione di questo
tipo si dice termodinamicamente favorita. Inoltre, dal rapporto delle concentrazioni dei prodotti e dei reagenti all’equilibrio
(cioè dal valore di K) si può determinare il rendimento massimo della reazione rispetto ai prodotti che interessano, ed esso è
tanto più grande quanto più elevato è il valore di K. Supponiamo ora che sia ∆G°>0, allora l’equilibrio è spostato verso i reagenti iniziali quanto più è grande il valore di ∆G°: queste reazioni sono termodinamicamente non favorite.
Espressione della costante di equilibrio per diversi tipi di reazione
1. Reazioni omogenee in fase gassosa
aA + bB + . . . ⇔ lL + mM + . . .
Se per ciascun componente gassoso si assume come stato standard lo stato di gas ideale alla pressione di 1 atm., allora:
a i = χ i Pi
χ * χ mM *. . . PLl * PMm *. . .
Kp =
*
χ * χ bB *. . . PAa * PBb *. . .
e ricordando che Pi = Xi * P e ponendo
∑υ
l
L
a
A
i
= ∆n :
χ lL * χ mM *. . . X lL * X mM *. . .
KP = a
*
* P ∆n
χ A * χ bB *. . . X aA * X bB *. . .
Se invece si assume come stato standard di ogni componente lo stato di gas ideale a concentrazione molare unitaria:
(a ) = (γ ) c
(γ ) * (γ ) *. . . c
*
=
(γ ) * (γ ) *. . . c
c
c
i
l
Kc
m
c
L
a
c
M
b
c
A
c
B
i
i
l
L
a
A
* c mM *. . .
* c bB *. . .
Le due costanti KP e Kc per una data reazione coincidono solo se è ∆n=0, altrimenti sono differenti, ma legate da una semplice
relazione, essendo
(a )
c
=
i
χ i Pi
RT
 1 
Kc = KP

 RT 
∆n
⇒ K P = K c (RT)∑
υi
Se nelle condizioni considerate i gas possono essere assunti come ideali allora i coefficienti diventano
χ i = (γ c ) i = 1 da cui
:
PLl * PMm *. . .
PAa * PBb *. . .
X lL * X mM *. . .
c lL * c mM *. . .
K
=
c
X aA * X bB *. . .
c aA * c bB *. . .
υ
∑υ
K P = K c ( RT) ∑ i = K X ( PT ) i
KP =
KX =
poiché per i gas perfetti Pi=ni/V * RT = ci * RT.
Osserviamo ora alcuni esempi:
• H2+I2
2HI ( acido iodidrico )
νi = 2 - 1 - 1 = 0
il numero di moli si mantiene e KP = Kc = KX
Dalle tabelle si trova che a 25°C, KP = 808. Questo dato si ottiene sfruttando la relazione ∆G°=-RT lnK e conoscendo
∆G°. Il massimo rendimento possibile è, visto che il rendimento termodinamico è sempre maggiore di quello cine-
Ù
tico:
KP =
Î
(c )
(c ) * (c )
H2
82
2
HI
I2
.
KX =
(X )
2
HI
(X ) * (X )
H2
 n HI 


 n TOT 
=
2
2
 n H 2   n I2

 *
 n TOT   n TOT
I2
2
n HI
N 2 (1 − α ) 4(1 − α )
=
=
=
= 808
Nα Nα
α2
 n H2 * n I2
*

2
2

4(1 − α ) = 808α 2 ⇒ −804α 2 − 8α + 4 = 0 ⇒ α = 6,6%
2
η = 100 - 6,6 = 93,4 %
Nei calcoli vale il seguente simbolismo:
• α = grado di dissociazione ( 0 < α < 1 )
• N = n° di moli dei prodotti
• Nα = n° di moli dei prodotti dissociate
• N(1-α) = n° di moli non dissociate
•
(rendimento massimo)
Nα
= n° di moli dei reagenti
2
Ù
Î
2NH3
• 3H2 + N2
KP = Kc (RT) -2 = KX (PT) -2
Σνi = 2 - 3 - 1 = 2
Spostamento dell’equilibrio
Quando un sistema chimico sia pervenuto all’equilibrio, la sua composizione dipende in generale dalle quantità iniziali delle
specie reagenti, dal volume del recipiente in cui la reazione si svolge, se a questa partecipano dei gas e dalla temperatura. Tra
questi fattori, l’unico che influisce sul valore della costante di equilibrio è la temperatura, ma anche una variazione di volume
può determinare un cambiamento della composizione della miscela. Questi effetti di spostamento dell’equilibrio come conseguenza di variazioni delle concentrazioni dei componenti o della pressione o della temperatura sono sinteticamente compendiati
nella legge di Le Chatelier (1888): Legge dell’equilibrio mobile: se si alterano le condizioni in cui si trova un sistema in equilibrio, variando uno qualunque dei fattori che ne determinano la posizione, l’equilibrio si sposta nella direzione che tende a ristabilire le condizioni iniziali.
1. Effetto di una variazione delle quantità dei componenti sull’equilibrio.
Alterando la composizione di un sistema chimico all’equilibrio, esso reagisce e la posizione dell’equilibrio si sposta: il senso di
lL + mM + ...
tale spostamento si desume dall’espressione della costante K. Consideriamo aA + bB + ...
Ù
Kc =
c lL * c mM *...
c aA * c bB *...
Se aumentiamo la concentrazione di A, il quoziente di reazione Q diminuisce al di sotto di K e la reazione riprende spontaneamente da sinistra a destra, diminuendo la concentrazione degli altri reagenti ed aumentando quella dei prodotti, in modo che
torni ad essere Q=K. Se invece viene aumentato L, allora diventa Q>K e la reazione retrocede verso sinistra..
2. Effetto della pressione sulla posizione di un equilibrio.
Per reazioni in cui partecipino componenti gassosi, la posizione dell’equilibrio è influenzata anche dalla pressione:
χ lL * χ mM *... X lL * X mM *...
KP = a
*
* P ∆n
χ A * χ bB *... X aA * X bB *...
Distinguiamo tre casi:
• ∆n > 0
Aumentando la pressione di lavoro, diminuisce il rapporto tra le frazioni molari dei prodotti e le frazioni molari dei
reagenti, ossia l’equilibrio si sposta verso i reagenti. Diminuendo la pressione P∆n diminuisce e KP impone che
aumenti il rapporto fra le quantità dei prodotti e dei reagenti, ossia l’equilibrio si sposta verso i prodotti finali, aumentando il rendimento della reazione. Esempi:
CH4 (g) + H2O (g)
CO (g) + 3H2 (g)
∆n = +2
H2O (g)
H2 (g) + ½ O2 (g)
∆n = + ½
CaCO3 (s)
CaO (s) + CO2 (g)
∆n = +1
In tutti questi casi una diminuzione della pressione fa avanzare maggiormente la reazione verso destra, mentre un aumento della pressione fa retrocedere la reazione verso sinistra.
• ∆n < 0
Il rendimento della conversione dei reagenti nei prodotti aumenta con la pressione. È per questa ragione che non poche importanti reazioni industriali allo stato gassoso si fanno avvenire sotto pressioni notevolmente alte. Vediamo
alcuni esempi:
Sintesi dell’ammoniaca
½N2 (g) + 3/2H2 (g)
NH3 (g)
∆n = -1
Ù
Ù
Ù
Æ
Ù
83
Æ
Æ
Ù
Ù
∆n = -2
Sintesi del metanolo
CO (g) + 2H2 (g)
CH3OH (g)
∆n = -1
Etanolo dall’etilene
C2H4 (g) + H2O (g)
C2H5OH (g)
• ∆n = 0
La reazione avviene praticamente senza variazione di volume e quindi la posizione dell’equilibrio (e di conseguenza
anche il rendimento relativo alla formazione dei prodotti) è indipendente dalla pressione alla quale avviene la reazione.
3. Effetto della presenza di gas inerti nella posizione dell’equilibrio in fase gassosa.
Si pensi a molte reazioni di ossidazione in fase gassosa, come la seguente:
SO2 (g) + ½O2 (g)
SO3 (g)
nelle quali si opera non con ossigeno puro, ma con aria contenente anche azoto (gas inerte): la sua presenza può alterare la posizione dell’equilibrio:
Ù
ni
χ lL * χ mM *.. . X lL * X mM *...
χ lL * χ mM *... n lL * n mM *...  P 
∆n
KP = a
*
* P ⇒ Xi =
*
*
⇒ KP = a

n TOT
χ A * χ bB *... X aA * X bB *...
χ A * χ bB *... n aA * n bB *...  n TOT 
∆n
La presenza di gas inerti in quantità maggiore o minore influisce tramite l’ultimo fattore facendo variare il numero totale di moli. Se si aggiungono gas inerti mantenendo costante la pressione, se ∆n > 0 l’equilibrio si sposta verso i prodotti, mentre se
∆n < 0 si sposta verso i reagenti.
4. Dipendenza della costante di equilibrio della temperatura.
A differenza degli altri fattori considerati fin qua, la temperatura influisce sulla posizione dell’equilibrio in una reazione chimica in quanto condiziona direttamente il valore stesso della costante K.
1 ∆ G°
*
R
T
d ln K ∆H°
=
dT
RT 2
ln K = −
dove ∆H° è il calore standard di reazione (a pressione costante). Questa formula è nota come equazione di Van’t Hoff. Da essa
d ln K
è determinato dal segno del calore standard di reazione ∆H°.
dT
d ln K
∆H° > 0
> 0 aumentando la temperatura, aumenta K e con essa
Reazioni endotermiche
dT
risolta che il segno della derivata
a)
Î
Î
Î
aumenta il rapporto di conversione dei reagenti nei prodotti e, in definitiva, il rendimento della reazione.
b)
Reazioni esotermiche
Î ∆H° < 0 Î d ln K < 0 Î aumentando la temperatura, diminuisce K e con essa
dT
diminuisce il rapporto di conversione dei reagenti nei prodotti e quindi il rendimento della reazione.
Equazione di Van’t Hoff
Studiando l’isoterma di reazione di Van’t Hoff, definendo la costante di equilibrio, abbiamo visto che possiamo esprimere
l’energia libera standard di reazione nella forma:
∆G° = -RT lnK
Consideriamo ora l’espressione differenziale dell’energia libera:
dG = dH -d(TS) = d(E + PV) -d(TS) = dE + PdV + VdP - TdS - SdT
ma in una trasformazione infinitesima reversibile si ha che TdS = δQ = dE + PdV.
DG = VdP - SdT
Osserviamo ora che in funzione delle variabili P e T, il differenziale è esprimibile in termini generali nella forma:
 ∂G 
 ∂G 
dG = 
 dP + 
 dT
 ∂P  T
 ∂T  P
si riconosce per confronto che:
 ∂G 

 =V
 ∂P  T
 ∂G 

 = −S
 ∂T  P
Pertanto l’espressione dell’energia libera G = H - TS può essere scritta:
 ∂G 
G = H + T

 ∂T  P
e, considerando una trasformazione isoterma accompagnata da una variazione di energia libera, diventa:
84
 ∂∆G 
∆G = ∆H + T

 ∂T  P
da cui, dividendo per T2:
∆G ∆H 1  ∂∆G 
= 2 + 

T  ∂T  P
T2
T
1  ∂∆G 
∆G
∆H

 − 2 =− 2
T  ∂T  P T
T
Si riconosce che il primo membro non è che la derivata rispetto alla temperatura di ∆G/T, sicché:
  ∆G  
 ∂  T  
H

 = −∆2
T
 ∂T 



P
Consideriamo ora lnK = - (∆G°/RT), derivandola rispetto a T:
 ∆G° 
d

 T 
d ln K
1
1  ∆H°  ∆H°
d ln K ∆H°
=− *
= − − 2  =
=
2 ⇒
dT
R
dT
R  T  RT
dT
RT 2
Quest’ultima è chiamata equazione di Van’t Hoff.
Equilibri ionici in soluzione
L’acqua è il miglior solvente dei sali e di ogni composto a struttura ionica o comunque con legami fortemente polari. Molti importanti processi industriali avvengono in soluzione acquosa e da soluzioni acquose è costituito l’ambiente dove si svolgono la
maggior parte dei processi biologici e molti fenomeni geologici.
La ionizzazione dell’acqua
L’acqua allo stato solido è costituita da aggregati di molecole legate l’una all’altra da legami ad idrogeno: anche se purissima,
rivela una conducibilità elettrica molto piccola, ma non nulla. Essa indica la presenza, in seno ad essa, di ioni. In realtà una piccolissima frazione di molecole è dissociata in ioni idrogeno H+ e ioni idrossido OH- :
H2O
H+ + OH+
Gli ioni H , però, non possono trovarsi liberi in soluzione, tendendo a coordinarsi a molecole d’acqua ed a formare ioni ossonio H3O+:
H+ + H2O
H3O+
H3O+ + OH-.
sicché l’equilibrio di ionizzazione dell’acqua risulta essere: 2H2O
+
Si hanno però fondate ragioni per ritenere che gli ioni H siano legati a 4 molecole d’acqua e che gli ioni OH- a 3 molecole
d’acqua. Quindi i primi sono presenti come aggregati di idratazione del tipo H9O4+ ed i secondi come aggregati del tipo H7O4-.
L’equazione scritta rappresenta la ionizzazione spontanea dell’acqua, detta anche autoprotolisi, perché qualunque processo che
in soluzione coinvolga il trasferimento di un protone è chiamato protolisi o reazione protolitica. L’equilibrio che esse descrivono è molto spostato a sinistra, perché la dissociazione ionica, riguarda un numero ridottissimo di molecole. Considerando che le
concentrazioni ioniche sono molto piccole, possono essere usate in luogo delle attività, per cui abbiamo:
Ù
Ù
Ù
[H ][OH ] ⇔ K ′ = [H O ][OH ]
K=
+
+
−
[H O]
2
−
3
[H O]
2
2
A temperatura costante, anche il prodotto K*[H2O] o K’*[H2O]2 che, indicato con KH2O, è definito prodotto ionico
dell’acqua, perché non è altro che il prodotto delle concentrazioni degli ioni H+ ed OH-. La legge dell’equilibrio diventa:
KH2O = [H+][OH-] ovvero KH2O = [H3O+][OH-]
Fissata la temperatura, il prodotto ionico dell’acqua è costante: il suo valore è funzione solo dalla temperatura e, a temperatura
costante, non è influenzata da variazioni delle concentrazioni, né da specie chimiche estranee. Quindi la formula è valida, non
solo per l’acqua pura, ma anche per qualunque soluzione acquosa ove sono contemporaneamente presenti ioni H+ e OH-. Il
prodotto ionico cresce con la temperatura perché il processo di ionizzazione è endotermico.
85
Soluzioni neutre, acide e basiche: pH e pOH
Nell’acqua pura gli ioni H+ e gli ioni OH- sono ovviamente in ugual numero. In una qualunque soluzione acquosa gli ioni H3O+
sono i portatori del carattere acido e gli ioni OH- i portatori del carattere basico. L’acqua pura è chimicamente neutra e [H3O+]
= [OH-] = 1,0 * 10-7 moli/litro (a 25°C), mentre se la concentrazione degli ioni H3O+ è maggiore di quella degli ioni OH-, la
soluzione è acida. Inversamente se la concentrazione degli ioni H3O+ è minore degli ioni OH- la soluzione è basica. Il carattere
acido, basico o neutro di una soluzione può dunque essere precisato mediante il valore [H3O+] o [OH-] indifferentemente, l’una
essendo legata all’altra dalla varianza del prodotto ionico: è consuetudine fare riferimento a [H3O+]. Di qui l’introduzione di
quella funzione della concentrazione degli ioni chiamata pH:
[
]
pH = − log 10 H 3 O + = log 10
1
[H O ]
+
3
Il pH esprime il logaritmo decimale della concentrazione degli ioni ossonio cambiate di segno. Per l’acqua pura risulta:
pH = - log10 (1,0 * 10-7) = 7
e questo è anche il valore del pH di ogni soluzione neutra. Per una soluzione acida, essendo [H3O+] > 10-7, è sempre pH < 7,
mentre per una soluzione basica, nella quale è [H3O+] < 10-7, è sempre pH > 7.
per HCl
0,1 M
pH = -log10 (10-1) = 1
per NaOH
0,1M
pH = -log10 (10-13) = 13
In generale si pone pK = -log10 K. Per una qualunque soluzione acquosa a 25°C si ha: pH + pOH = 14.
Acidi e basi
Teoria di Arrhenius = una qualunque specie chimica che dissociandosi in soluzione fornisce ioni idrogeno, è un acido. Mentre una qualunque specie che dissociandosi in soluzione fornisce ioni idrossido è una base.
+
−
HA
H ⇔
+A
+
−
MOH
M
⇔
+ OH
ACIDO
BASE
Secondo questa teoria, ogni reazione di neutralizzazione di un acido con una base non è che una reazione di combinazione tra
gli ioni H+ dell’uno e gli ioni OH- dell’altra, con la formazione di molecole d’acqua indissociate, mentre in soluzione resta, dissociato nei suoi ioni, un sale:
+ Cl ]
+ [ Na + OH ]
⇒ [ Na + Cl ]
+H O
[H
+
−
+
−
soluzione
+
−
soluzione
ACIDO
soluzione
BASE
2
SALE
Î
Teoria di Bronsted-Lowry = ogni specie, molecolare o ionica, capace di cedere un protone, è un acido, mentre ogni specie
capace di fissare un protone è una base
un acido è un donatore di protoni mentre una base è un accettore di protoni.
In ogni caso, ad un acido forte, corrisponde una base coniugata debole.
Sono acidi forti
Sono basi forti
HClO4
H+ + ClO4- (acido perclorico)
OH- + H+
H2O (ione idrossido)
HNO3
H+ + NO3- (acido nitrico)
O2- + H+
OH- (ione ossido)
+
+
H2SO4
H + HSO4 (acido solforico)
NH2 + H
NH3 (ione ammonio)
HCl
H+ + Cl- (acido cloridrico)
CO32- + H+
C2H5OH (ione carbonato)
Un acido, si è detto, è un donatore di protoni: ma perché un protone possa separarsi dalla molecola di un acido, è necessario
che sia presente una base che abbia tendenza a fissarlo strappandolo alla molecola madre. Il protone libero non può sussistere:
la liberazione di un protone da parte di un acido, comporta il suo trasferimento ad una base. Questo processo di trasferimento di
protoni è detto protolisi.
A1
B 1 + H+
Perché possa avvenire questo processo, è necessaria la presenza di una base B2 che fissi il protone per trasformarsi nell’acido
coniugato A2:
A1 + B 2
B 1 + A2
L’acqua può comportarsi sia come base che come acido: il duplice comportamento deriva dal fatto che la sua molecola può acquistare un protone o cederlo, a seconda dei casi:
Ù
Ù
Ù
Ù
Ù
Ù
Ù
Ù
Ù
Ù
Le molecole e gli ioni che hanno questa caratteristica sono definiti anfoliti o elettroliti anfoteri. Quando il trasferimento di protoni avviene tra molecole della stessa specie, si parla di autoprotolisi. Ionizzazione dell’acqua:
−
+
H 2 O + H 2 O ⇔ OH
3O
+ H
, ,
( A1 )
86
( B2 )
( B1 )
( A2 )
I liquidi che partecipano a processi di trasferimento di protoni (benzene C6H6 ...) sono detti aprotici. È importante specificare
che non si può parlare di forza di un acido o di una base in senso assoluto. In soluzione, la forza di un acido cresce con
l’aumentare del carattere basico del solvente e la forza di una base cresce con l’aumentare del suo carattere acido. In soluzione
acquosa, tutti gli acidi più forti di H3O+ si ionizzano in modo completo cedendo il loro protone all’acqua: così HClO4, H2SO4,
HCl, HNO3 di diversa forza assoluta, risultano ugualmente dissociati in acqua. L’acqua cioè esplica nei confronti di questi acidi un effetto livellante nel senso che ne annulla le differenze facendoli apparire egualmente forti:
Gli acidi che invece sono più deboli di H3O+ si ionizzano solo parzialmente in soluzione acquosa, pervenendo ad un equilibrio
la cui posizione è determinata dalla forza dell’acido in confronto con H3O-. Il diverso comportamento in soluzione degli acidi
più forti di H3O+, totalmente ionizzati e di quelli più deboli, ionizzati solo parzialmente, corrisponde alla regola generale che le
reazioni di trasferimento di protoni tendono ad avvenire nel senso che porta alla formazione dell’acido e della base più deboli.
La costante di equilibrio termodinamico di un acido si indica con Ka , detta costante di dissociazione acida , da cui si ottiene:
pKa = - log10 Ka
Quanto più acido è debole, tanto più grande è il valore del suo pKa. Considerazioni parallele si possono fare per le basi. Tutte
le basi più forti di OH- in soluzione reagiscono totalmente con l’acqua fissando un protone e liberando questo ione. Le proprietà basiche di queste soluzioni sono determinate dalla presenza della base OH-, comune a tutti e quindi, a parità di normalità, la
loro basicità è equivalente:
Le basi che invece sono più deboli di OH- (come NH3, CO32-) non reagiscono quantitativamente con l’acqua ed in soluzione si
stabilisce un equilibrio la cui posizione è determinata dalla forza della base considerata in confronto con OH-. La costante di
equilibrio termodinamico è detta costante di ionizzazione basica Kb , da cui:
pKb = - log10 Kb
Quanto più una base è debole, tanto più grande è il valore del suo pKb. È immediato verificare che per qualunque coppia di un
acido e di una base coniugati, il prodotto Ka*Kb , riferendosi a soluzioni acquose, è uguale al prodotto ionico dell’acqua:
ÙH O +A
HA + H O
+
2
A- + H2O
3
Ù HA + OH
[H O ][A ]
=
+
-
-
Ka
Ka =
−
3
[HA]
[HA][OH − ]
[A ]
−
Ka - Kb = [H3O+][OH-] = KH2O = 1,0 * 10-14 (a 25°C)
pKa + pKb = 14
Ionizzazione di un acido o di una base in soluzione acquosa
Gli acidi più forti di H3O+ e le basi più forti di OH- in soluzione acquosa si ionizzano quantitativamente, mentre gli acidi e le
basi più deboli si ionizzano solo parzialmente ed il grado di ionizzazione è regolato da un equilibrio la cui posizione dipende
dalla forza relativa dell’acido o della base.
87
Acidi e basi monoprotici
Si consideri un acido forte monoprotico HA: esso è totalmente ionizzato e la sua ionizzazione porta in soluzione c moli di
H3O+ per litro, a cui si aggiungono gli ioni H3O+ provenienti dalla ionizzazione dell’acqua (trascurabili):
HA + H2O
A- + H3O+
+
La concentrazione degli ioni H3O si ottiene imponendo le condizioni di elettroneutralità della soluzione e di invarianza del
prodotto ionico dell’acqua:
1. [H3O+] = [A-] + [OH-] = c + [OH-]
[OH-] = KH2O / [H3O+]
2. KH2O = [H3O+] [OH-]
da cui si ottiene:
Î
Î
[H O ] = c +
+
3
K H 2O
[H O ]
+
[
⇔ H 3O +
]
2
[
]
− c H 3 O + − K H 2O = 0
3
c + c 2 + 4K H 2O
[H O ] =
+
3
-6
c > 10 moli*litro-1
-8
c < 10 moli*litro
-1
Î [H O ] = c
2
Î [H O ] =
+
3
+
e
pH = - log10 c
K H 2O = 10-7 e pH = 7
3
Considerazioni analoghe per basi monoprotiche forti MOH:
c + c 2 + K H 2O
[OH ] =
−
Î
2
[OH-] = c , pOH = -log10 c , pH = 14 + log10 c
c > 10-6 moli*litro-1
-8
[OH-] = 10-7 , pOH = pH = 7
c < 10 moli*litro-1
Passiamo ora a considerare un acido debole monoprotico di tipo HA. In soluzione acquosa esistono gli equilibri:
HA + H2O
H3O+ + A2H2O
H3O+ + OHregolato dalle seguenti condizioni:
Î
Ù
Ù
[
]

H 3 O + [A − ]
K a =
[H A ]

K
+
−
 H 2O = H 3 O [O H ]

−
 c = [H A ] + [ A ]
 H O + = OH − + A −
[
] [ ]
3

[
[
]
]
risolvendo il quale si ottiene:
c > 10
-6
Î [H O ] >> K Î [H O ] = − K
moli*litro
[H O ]
Î K = [H O ] Î [H O ] =
c >> [H O ]
H 2O
+
-1
+
+
3
a
+ K a 2 + 4K a * c
3
2
3
+
2
3
+
a
3
+
3
c
K ac
pH = ½ pKa – ½ log10 c
Una trattazione del tutto analoga può essere sviluppata per le soluzioni di basi deboli monoiprotiche B:
[OH ] >>
−
K H 2O
[OH ]
−
⇒ [ OH
c >> [OH-]
−
]=
− K b + K b 2 + 4K b * c
Î [OH ] =
−
2
Kb *c
pH = pKH2O – ½ pKb + ½ log10 c
Processi idrolitici
Si indicano col nome di idrolisi i processi di scambio protonico in soluzione tra l’acqua ed anioni o cationi che siano rispettivamente basi coniugate di acidi deboli o acidi coniugati di basi deboli. In seguito a questi processi viene alterato l’equilibrio tra
88
gli ioni H3O+ ed OH- proprio dell’acqua pura e la soluzione non risulta essere più neutra. Ogni volta che si scioglie in acqua un
sale avente le caratteristiche sopra riportate, si ha idrolisi e la soluzione diventa acida o basica secondo che gli ioni dissolti cedano protoni all’acqua (ioni acidi) o ne sottraggono (ioni basici). Quando si scioglie un sale in acqua, i suoi ioni secondo la loro
natura possono con l’acqua interagire in modi diversi: possono cioè semplicemente legarsi ad un certo numero di molecole di
acqua (si parlerà di idratazione) o possono con essa reagire scambiando protoni, col meccanismo delle reazioni acido-base (si
parlerà di idrolisi). La semplice idratazione è propria dei metalli alcalini ed alcalino-terrosi (Li+, Na+, Mg2+, …) e degli ioni
degli acidi forti (ClO2-, NO3-, Cl-, …). Un esempio di idratazione, in cui le soluzioni permangono neutre è:
Na+(aq) + Cl-(aq)
NaCl + nH2O
K+(aq) + NO3-(aq)
KNO3 + nH2O
Invece gli anioni degli acidi deboli che hanno una notevole affinità per il protone (come CN-, S2-, CO32-,…) e certi cationi che
hanno accentuate caratteristiche di donatori di protoni (NH4+,…) si idrolizzano in soluzione scambiando protoni con l’acqua.
Esaminiamo ora un po’ in dettaglio questi processi. Cominciamo dall’idrolisi degli anioni di acidi deboli:
A- + H2O
HA + OHSe contemporaneamente all’anione non si idrolizza anche il catione del sale disciolto, la soluzione è basica, tanto quanto più è
debole l’acido HA. La costante di equilibrio è detta costante di idrolisi:
Î
Î
Ù
K i = (K b ) A − =
[HA][ OH − ]
[A ]
−
K H 2O
Ki =
(K )
a HA
c >> K i ⇒ pH =
1
1
1
pK H 2O + pK a + log 10 c
2
2
2
Inoltre si definisce grado di idrolisi di un sale la frazione di esso che in soluzione si idrolizza:
χi =
[HA]
c
Ki
c
=
Ù
In modo analogo si può trattare l’idrolisi dei cationi esplicanti caratteristiche acide:
B + H3O
BH+ + H2O
Se non si idrolizza col catione anche l’anione del sale disciolto, la soluzione è acida, tanto più quanto più è debole la base B.
Ki =
[B ][H 3 O + ]
Ki =
[BH ]
+
K H 2O
(K )
b B
1
1
1
pK H 2O − pK b − log 10 c
2
2
2
[B ] = K i
χi =
c
c
c >> K i ⇒ pH =
Soluzione tampone
Una soluzione acquosa contenente insieme un acido debole HA e la sua base coniugata A-, oppure una base debole B ed il suo
acido coniugato BH+, in concentrazioni circa uguali, ha la proprietà di mantenere il proprio pH pressoché costante quando ad
essa si aggiungano piccole quantità di un acido o di una base e per questa caratteristica, essa viene chiamata soluzione tampone.
pH = pK a + log 10
[sale]
[acido]
Concetto di acido e base secondo Lewis
Lewis ha studiato, insieme col processo di trasferimento dei protoni, anche altri processi analoghi che non coinvolgono scambi di protoni. Le proprietà di una base sono da attribuire alla presenza in essa di una coppia elettronica non condivisa con la quale può legare un protone:
cioè tutte le specie chimiche con una o più coppie elettroniche non condivise possono reagire
come basi e tutte le specie chimiche contenenti atomi con gli orbitali di valenza incompleti, così
da poter accogliere coppie elettroniche da una base, legandosi ad essa con legami di coordina89
zione, possono reagire come acidi. La condivisione di una coppia di elettroni in un legame coordinativo tra una base ed un acido, realizza la neutralizzazione della base con l’acido: il composto che si forma è un complesso di coordinazione (detto anche
addotto). Le basi di Brönsted sono anche basi per Lewis, ma gli acidi del primo sono per Lewis dei complessi di un acido con
una base: l’acido è il protone (non la molecola o lo ione donatore del protone) e la base è la base coniugata di Brönsted. Sono
acidi: BF3, AlCl3, Ag+, Mg2+,….; sono basi: O2-, S2-, F-, Cl-, …
Equilibri di solubilità di composti ionici
Gli equilibri ionici in soluzione trattati sino ad ora sono tutti omogenei: ora analizzeremo equilibri eterogenei che riguardano le
soluzioni sature di composti ionici poco solubili. Si consideri un generico composto ionico Bυ+ Aυ- formato da ioni Bz+ e Az- in
soluzione satura. Si stabilisce l’equilibrio di solubilità:
Bυ+ Aυ- (s)
υ+Bz+(aq) + υ-Az-(aq)
Se il composto considerato è poco solubile, le concentrazioni dei suoi ioni nella soluzione sono molto piccole, la soluzione
stessa può essere trattata come ideale (cioè possiamo esprimere K con le concentrazioni):
Ù
[B ] [A ]
K=
[B Aν − ]
Z+
ν+
Z−
ν−
ν+
Ma trattandosi di un equilibrio eterogeneo, dato che il composto indisciolto costituisce una fase solida pura, [Bν+Aν-] è conglobato in K stessa e si definisce così il prodotto di solubilità:
K ps = [ B Z + ]
ν+
[A ]
Z−
ν−
Il prodotto di solubilità no è altro che l’espressione della costante di equilibrio relativa all’equilibrio di solubilità di un composto ionico: il suo valore, quindi, per un dato composto dipende solo dalla temperatura e se la temperatura è costante, non varia
aggiungendo alla soluzione altri soluti. Se nella soluzione satura di un composto ionico si introduce un eccesso di una delle
specie ioniche da cui esso è costituito la sua solubilità diminuisce (effetto degli ioni comuni).
Equilibri tra fasi diverse
L’applicazione dei criteri dell’equilibrio termodinamico ai sistemi polifasici porta alla formulazione della regola delle fasi che
definisce, in funzione del numero dei componenti del sistema considerato e delle fasi che vi coesistono in equilibrio, il numero
delle variabili indipendenti. Gradi di libertà del sistema – in gergo chimico varianza – cioè il numero di variabili che col loro
valore ne determinano completamente lo stato, in condizioni di equilibrio. È importante rilevare che le condizioni di equilibrio
in un sistema polifasico sono indipendenti dall’effettiva quantità delle singole fasi.
La regola delle fasi
Si consideri un sistema formato da C specie chimiche distinte distribuite in F fasi, supponendo per il momento che ognuna di
esse sia presente in tutte le fasi e che nel sistema non abbia luogo nessuna reazione. Lo stato di una fase è individuato dalla
temperatura, dalla pressione e dalla composizione, che a sua volta resta definita dalle frazioni molari Xi di C-1 componenti. Per
l’intero sistema, il numero totale di variabili (Mtot):
Mtot = F ( C+1 )
Però in condizioni di equilibrio, solo una parte di essi può assumere valori arbitrari, essendo tutte insieme vincolate dalle equazioni che esprimono quelle condizioni. Il numero delle variabili indipendenti N, è calcolabile sottraendo dal numero di variabili
totali il numero Meq di dette equazioni:
N = Mtot -Meq
L’equilibrio termico comporta l’uguaglianza della temperatura in tutte le fasi. L’equilibrio meccanico impone poi che in tutte le
fasi la pressione sia la stessa. Infine l’equilibrio chimico impone che l’energia libera molare Gi di ciascun componente sia uguale in tutte le fasi. Si ha dunque:
Meq = ( F-1 ) + ( F-1 ) + C( F-1 ) = ( F-1 ) ( C+2 )
e quindi si ottiene:
N=C+2–F
Questa equazione esprime la regola delle fasi quando fra i componenti del sistema non avvenga alcuna reazione. Supponiamo
che un certo numero di componenti partecipa a nR reazioni indipendenti l’una dall’altra. Pertanto ora le equazioni che vincolano le variabili del sistema sono in numero maggiore:
Meq = ( F-1 ) ( C+2 ) + nR
ne deriva:
N = Mtot – Meq = F( C+1 ) – { ( F-1) ( C+2 ) + nR } = ( C-nR ) + 2 – F
Pertanto, ponendo C’ = C – nR, otteniamo:
N = C’ + 2 – F
90
Ogni vincolo addizionale (di tipo stechiometrico) è equivalente ad una relazione in più tra le variabili del sistema. Risulta (detto
nV il numero di equazioni addizionali):
Meq = ( F-1 ) ( C+2 ) + nR + nV
N = ( C – nR – nV ) + 2 – F
( regola delle fasi generalizzata )
La regola delle fasi può essere formulata nei termini più generali dicendo che il numero delle variabili indipendenti di un sistema polifasico in equilibrio costituito da un numero qualunque di specie chimiche è dato dal numero di componenti chimici indipendenti, più quello delle variabili fisiche necessarie per definire lo stato del sistema, meno il numero delle fasi.
Sistemi ad un solo componente
Si consideri un sistema costituito da un’unica specie chimica presente in due fasi diverse fra loro in equilibrio. Il sistema è monovariante. Alla temperatura ed alla pressione alla quale si considera il sistema, essendo questo in equilibrio, deve essere:
G(1) = G(2)
Indicando con G l’energia libera molare dell’unica specie presente e con l’indice tra parentesi la fase alla quale ci si riferisce.
Se T e P variano di dT e dP, affinché l’equilibrio si conservi, deve essere dG(1) = dG(2) e ricordando che dG = VdP – SdT:
V(1) dP – S(1) dT = V(2) dP – S(2) dT
(1)
(2)
dove V e V sono i volumi molari della specie chimica considerata nelle due fasi ed S(1) e S(2) le corrispondenti entropie molari.
dP
S ( 2 ) − S ( 1)
∆S
= ( 2)
( 1) =
dT V − V
∆V
[S ( 2 ) − S ( 1) ]dT = [ V ( 2) − V ( 1) ]dP ⇒
indicando con ∆S e ∆V la variazione di entropia e di volume molare che accompagna la trasformazione dalla fase 1 alla fase 2.
In condizioni di equilibrio tra le due fasi, quando G(1) = G(2) , la transizione tra le fasi stesse è reversibile e quindi:
S ( 2 ) − S (1) =
(1)
∫
fase 2
fase 1
1
δQ
=
T
T
∫
fase 2
fase 1
δQ =
H ( 2 ) − H (1)
L
∆H
=
=
T
T
T
(2)
dove, essendo H e H le entalpie molari nelle due fasi, L indica l’effetto termico che accompagna, alla pressione corrispondente alla temperatura T, la trasformazione di fase considerata, ossia il calore latente della trasformazione stessa.
Quindi:
dP
L
=
dT T * ∆V
che è la forma classica della equazione di Clausius-Clapeyron: essa definisce per i sistemi ad un solo componente, le condizioni di equilibrio tra due fasi qualunque: integrata fornisce i valori di T e P per i quali le fasi considerate coesistono in equilibrio
fra loro. Consideriamo l’equilibrio tra una fase condensata, liquida o solida, e la fase vapore:
∆V = VVAP e VVAP = RT / P
dP
L
dP
L
dT
=
=
2 P ⇒
dT RT
P
RT 2
Consideriamo in prima approssimazione il calore latente L indipendente dalla temperatura. Integro ed ottengo:
ln P = −
L
L
−
+ cos t ⇒ P = A * e RT
RT
Passando a considerare ora l’equilibrio tra due fasi condensante è conveniente esprimere l’equazione nella forma:
dT T * ∆V
=
dP
L
Consideriamo l’equilibrio solido-liquido. Essendo L>0, dT/dP dipende solo da ∆V:
1. ∆V>0 se la densità del solido è maggiore del liquido e risulta dT/dP>0, ossia se la temperatura di fusione cresce al crescere della pressione;
2. ∆V<0, allora dT/dP<0, ossia la temperatura di fusione diminuisce al crescere della pressione (come nel caso dell’acqua).
dT ∆V
dP
=
T
L
ln
,
ln
T2 ∆V
=
∆P
T1
L


T2
T1 + T2 − T1
T2 − T1 
∆T  ∆T
 = ln 1 +
 ≈
= ln
= ln 1 +
T1
T1
T1 
T1  T1


da cui risulta in conclusione che:
∆T = T1 *
∆V
∆P
L
91
La variazione del punto di fusione è dunque proporzionale alla variazione di pressione e la curva che descrive le condizioni P,T
di equilibrio è praticamente una retta.
Diagrammi di stato dei sistemi ad un solo componente
I diagrammi di stato dei sistemi ad un solo componente precisano i campi
di esistenza delle diverse possibili fasi e le condizioni di equilibrio tra le
fasi medesime: vi sono riportate nel piano P-T le curve rappresentative
degli equilibri. Ogni punto di incontro fra due curve del diagramma è un
punto triplo che definisce le condizioni nelle quali coesistono in equilibrio
tre fasi. Il punto triplo T corrisponde, per l’acqua, alla pressione di 4,58
mmHG ed alla temperatura di 0,0098 °C. Il punto triplo dell’acqua, per la
sua invarianza e la sua riproducibilità, è assunto come punto termometrico
fondamentale di riferimento: sulla scala Kelvin delle temperature corrisponde a 273,16 K.
TC = pressione di vapore dell’acqua liquida fina al punto critico C: descrive le condizioni di equilibrio fra fase liquida e fase vapore.
TA = pressione di vapore del ghiaccio: definisce le condizioni di equilibrio tra fase solida e fase vapore.
TB = variazione della temperatura di fusione del ghiaccio al variare della pressione.
92
Termodinamica Elettrochimica
Considerazioni introduttive
Considereremo ora due tipi di processi: da un lato processi chimici che hanno la possibilità di compiersi spontaneamente e che,
realizzati in opportune condizioni, possono essere sfruttati come sorgenti di energia elettrica (processo elettromotore);
dall’altro processi chimici che non potrebbero avvenire spontaneamente e che possono invece essere realizzati fornendo energia
elettrica ad appropriati sistemi (processo di elettrolisi). Quanto ai primi è da considerare che una reazione di ossidoriduzione
spontanea può diventare una sorgente di energia elettrica quando sia fatta avvenire in modo che gli elettroni messi a disposizione dalla specie riducente a quella ossidante non si trasferiscano dall’una all’altra in una serie di atti elementari di trasmissione
diretta, ma vengano convogliati in un flusso ordinato attraverso un conduttore metallico che li trasporti dal sistema che si ossida
a quello che si riduce, tenuti separati: il flusso ordinato di elettroni nel conduttore metallico è corrente elettrica. Queste condizioni sono realizzate nelle pile o celle chimiche. Limiteremo i nostri studi alle pile reversibili, le sole alle quali possono essere
applicate le equazioni dell’equilibrio termodinamico perché per costruzione, quando non erogano corrente, non si ha nessuna
trasformazione.
Generalità sui potenziali elettrodici
Una cella chimica reversibile è costituita da due semielementi: durante il suo funzionamento come sorgente di energia elettrica
in uno di essi si compie un processo di ossidazione che libera elettroni e nell’altro un processo di riduzione che li utilizza. Ogni
semielemento è formato da un elettrodo conduttore immerso in un sistema elettrolitico. Tra l’elettrodo e l’elettrolita a contatto
si stabilisce una differenza di potenziale. Immergiamo una barra di metallo M in una soluzione acquosa: alcuni atomi di superficie passano in soluzione come ioni idratati:
Mz+(aq) + zeM(s) + nH2O
ed alcuni ioni del metallo dalla soluzione si depositano nella barra legandosi nel reticolo cristallino:
M(s) + nH2O
Mz+(aq) + ze1. Supponiamo che sia più accentuata la prima reazione. A mano a mano che atomi del metallo
passano in soluzione come ioni, il metallo diventa mano a mano più negativo e tende perciò a
mandare nuovi ioni in soluzione sempre meno facilmente, così che la velocità del processo va
progressivamente decrescendo. Si perverrà così ad uno stato di equilibrio tra i due processi:
Mz+(aq) + zeM(s) + nH2O. Questo determina all’iterfase tra elettrodo e soluzione un doppio
strato elettrico che in questo caso ha la faccia negativa sul metallo e la faccia positiva nella
soluzione che si arricchisce di ioni Mz+. Il doppio strato comporta una differenza di potenziale che
dipende dalla posizione dell’equilibrio, tanto maggiore quanto più l’equilibrio è spostato a sinistra.
2. Se invece è maggiore la tendenza degli ioni Mz+ a passare dalla soluzione sulla superficie del metallo, all’equilibrio si viene ad avere il metallo carico positivamente.
Nell’un caso e nell’altro, a equilibrio raggiunto, la differenza di potenziale all’interfase si mantiene costante, perché rimane stazionaria la struttura del doppio strato. Consideriamo ora due diversi semielementi formati da elettrodi di metallo diversi immersi in soluzioni contenenti i loro ioni. All’interfase metallo-soluzione si ha:
MIz’+(aq) + z’eMI(s) + nH2O
MII(s) + nH2O
MIIz’’+(aq) + z’’eIl doppio strato elettrico che caratterizza la regione di contatto elettrodo-soluzione, determina nei due casi differenze di potenziale diverse. Se ora i due elementi vengono accoppiati, mettendo a contatto le due soluzioni elettrolitiche in cui le barrette metalliche sono immerse, in maniera da impedirne il rapido mescolamento pur consentendo un lento trasporto ionico dall’una
all’altra, si realizza una cella chimica. L’accoppiamento dei due semielementi può essere attuato utilizzando un recipiente diviso in due scomparti da una setto poroso o congiungendoli mediante un ponte salino ripieno di una appropriata soluzione salina
(KCl, K2SO4…), recante alle due estremità due tappi porosi.
Vediamo ora cosa succede quando i due elettrodi vengono collegati attraverso un circuito conduttore esterno alla cella. Stabilito il collegamento prende il via una travaso di elettroni, attraverso il circuito esterno dell’elettrodo che ne ha in maggior copia a
quello che ne ha meno, facendo così fluire attraverso il circuito stesso una corrente elettrica. Questo travaso di elettroni
dall’uno all’altro elettrodo, altera ovviamente gli equilibri, spostando a sinistra quello relativo all’elettrodo da cui gli elettroni
muovono e a destra quello relativo all’altro elettrodo che li riceve:
MI(s) + nH2O
MIz’+(aq) + z’ez’’+
MII(s) + nH2O
MII (aq) + z’’e
Il processo globale che avviene nella cella durante il suo funzionamento non è che la risultante delle due semireazioni elettrodiche, ossia è una ossidoriduzione. Accoppiando un semielemento formato da un elettrodo di zinco in una soluzione di solfato di
zinco - contenente ioni Zn2+(aq)- con un semielemento formato da un elettrodo di rame immerso in una soluzione di solfato di
rame - contenente ioni Cu2+(aq)- si ottiene un classica pila di Daniel:
Zn2+(aq) + 2eZn (s) + nH2O
Î
Î
Ù
Ù
Ù
Ù
Ù
Ù
93
Ù
Cu2+(aq) + 2eCu (s) +nH2O
Se gli elettrodi vengono collegati tra loro attraverso un circuito esterno, l'eccesso di elettroni immagazzinato nell'elettrodo di
zinco, si riversa in quello di rame, spostando a sinistra il primo equilibrio e a destra il secondo. Il processo globale è:
Zn (s) + Cu2+ (aq)
Zn2+ (aq) + Cu (s)
L'elettrodo di zinco progressivamente si consuma e quello di rame si accresce. L'anodo è la sorgente degli elettroni e costituisce
l'elettrodo negativo, mentre il catodo è lo scarico che li elimina e costituisce l'elettrodo positivo. Questo in quanto, rispetto al
processo di elettrolisi, i segni sono cambiati. Merita un momento di considerazione la giunzione tra i due semielementi. Quando
i due elettrodi della cella vengono collegati attraverso un circuito conduttore e la reazione si avvia, nelle vicinanze dell'elettrodo di rame resta momentaneamente un eccesso di ioni negativi in seguito alla trasformazione
Cu2+(aq) + 23eCu (s) +nH2O che dalla soluzione elimina un certo numero di ioni Cu2+, mentre nelle vicinanze dell'elettrodo di zinco si viene ad avere momentaneamente un eccesso di ioni positivi. A riequilibrare continuamente questo sbilancio
di cariche ioniche che la reazione di ossidoriduzione provocherebbe nei due semielementi della cella in vicinanza degli elettrodi, così da conservare in ogni punto l'elettroneutralità del sistema, provvede la diffusione degli ioni delle soluzioni elettrolitiche
dei due elementi attraverso il setto poroso o il ponte salino.
Î
Î
Tipi di semielementi galvanici
I semielementi che costituiscono una cella galvanica possono essere di diversi tipi:
1. Semielementi di prima specie. Sono costituiti da un metallo immerso nella soluzione di un suo sale (pila Daniell).
2. Semielementi di seconda specie. Sono formati da un elettrodo metallico a contatto con una fase solida costituita da un sale
poco solubile del medesimo metallo e con una soluzione di un elettrolita avente l'anione in comune con il sale indisciolto
(elettrodo ad argento - cloruro d'argento, elettrodo a calomelano).
3. Semielementi a gas. All'equilibrio che si stabilisce all'interfase tra l'elettrodo e la soluzione partecipano un gas ed una o più
specie presenti nella soluzione (elettrodo ad idrogeno: H3O+(aq)+e- ½H2 (q) + nH2O).
4. Semielementi ad amalgama. Sono analoghi a quelli di prima specie con la differenza che il metallo partecipante all'equilibrio di scambio elettronico con i suoi ioni in soluzione, invece di essere allo stato puro, è disciolto in un altro metallo che
non prende parte al processo e fa da supporto inerte. Se il metallo usato è il mercurio, si realizza un elettrodo ad amalgama.
5. Semielementi di ossidoriduzione. Sono caratterizzati dall'equilibrio di scambio elettronico fra i due membri di una coppia
coniugata di ossidoriduzione, entrambi in soluzione: nella soluzione è immerso un elettrodo metallico inerte, che ha la sola
funzione di trasportare gli elettroni.
Ù
Forza elettromotrice di una cella chimica
Il collegamento tra i due elettrodi di una cella chimica mediante un circuito esterno, mette in
moto un flusso continuo di elettroni, alimentato dal processo ossidoriduttivo che in essa, in
queste condizioni, si svolge. La cella esegue dunque un lavoro elettrico, trasportando gli
elettroni dall'uno all'altro elettrodo a potenziale diverso. In condizioni di reversibilità, questo
lavoro, che è il lavoro utile compiuto dal nostro sistema, eguaglia la diminuzione di energia
libera che accompagna lo svolgersi della reazione. Esplicitando questa reazione è data la
forza elettromotrice reversibile di una cella. È necessario che la cella stessa sia in equilibrio
termodinamico
e quindi non eroghi corrente. Queste condizioni si realizzano quando la forza
Potenziometro
elettromotrice viene misurata col dispositivo potenziometrico in figura. Il lavoro elettrico
che la cella compie sull'esterno quando la reazione di ossidoriduzione, che costituisce il
Cella di alimentazione
processo elettromotore, progredisce di un infinitesimo è uguale, in valore assoluto, a:
δW' = -E dq
-(dG)T,P = E dq
dove con E viene indicata la forza elettromotrice (f.e.m.). La reazione di ossidoriduzione della cella sia:
aRI + bOII
a'OI + b'RII
La variazione di energia libera che accompagna un avanzamento infinitesimo:
(dG)T,P = (∆G)T,P * dξ
Questa trasformazione è accompagnata dal trasferimento di n moli di elettroni, ossia di n Faraday. Un incremento dξ del grado
di avanzamento è accompagnato dal trasporto di una quantità di elettricità n* dξ moli di elettroni, pari a nƒ dξ Coulomb (con ƒ
costante di proporzionalità tra Faraday e Coulomb) :
-(dG)T,P = (∆G)T,P * dξ = E nƒ dξ
E = - (∆G)T,P / nƒ
Essendo:
Cella oggetto della misura
Î
(∆G )T , P
(
= ∆G o
)
T
+ RT ln
a a ′ O I * a b′ R II
a a R I * A b O II
Si ottiene:
94
 o
∆G o RT
ln k
E
=
−
=

nf
nf


a′
b′
 E = E o − RT ln a O I * a R II

nf
a a R * a bO
che, nota come equazione di Nernst, definisce la forza elettromotrice reversibile della cella in funzione della composizione del
sistema elettrochimico e della temperatura, dove E° è la f.e.m. standard.
Potenziale di un semielemento. Serie elettrochimica dei potenziali standard
o normali.
La forza elettromotrice reversibile di una cella galvanica è la differenza di potenziale fra i suoi elettrodi quando essa non eroga
corrente. Realizzata una qualunque cella galvanica, il segno dei suoi elettrodi può essere ricavato direttamente dalla misura potenziometrica della sua forza elettromotrice. Infatti le condizioni di equilibrio tra la forza elettromotrice della cella ed il contropotenziale applicato si possono realizzare solo se la cella è inserita nel circuito in opposizione rispetto alla polarità dell'alimentatore dello strumento di misura e quindi è immediatamente identificabile l'elettrodo positivo e quello negativo.
• Elettrodo negativo
semireazione di ossidazione
• Elettrodo positivo
semireazione di riduzione
Per la forza elettromotrice si assume il seguente segno:
∆G < 0
E>0
∆G > 0
E<0
In entrambi i casi la f.e.m. della cella è esprimibile come differenza tra il potenziale positivo e quello dell'elettrodo negativo,
assumendo per ciascuno il proprio segno. Trasformando l'equazione di Nernst:
Î
Î
E = Eo −
Î
Î
′
′
′
′
′
RT a a O I * a b R II
RT a a O I RT a b R II
RT a b R II  RT a a R I
o
o
=
−
−
=
−
− −
ln a
ln
ln
ln
ln a′
E
E
nf
nf
nf
nf
a R I * a b O II
a a RI
a b O II
a b O II  nf
a OI




e ponendo:
E o = E o O II − E o O I
R II
RI
risulta:
b′

 RT
a a R 
RT a R II   o
ln b
ln a′ I  
E =  E o o II −
 −  E o I −  −
nf
a O II   R I  nf
a O I  
 R II
Le espressioni entro parentesi quadre sono i potenziali dei due semielementi della cella RI|OI||OII|RII, formati dalle coppie coniugate OI-RI e OII-RII, in riferimento alla reazione di ossidoriduzione della cella aRI + bOII a'OI + b'RII le cui semireazioni
sono:
a'OI + neaRI
b'RII
bOII + neQuando le attività dei componenti della coppia redox di un semielemento sono unitarie, il suo potenziale diventa uguale a E°O/R
e prende il nome di potenziale standard del semielemento considerato: il suo valore viene definito per confronto col potenziale
di un adatto elettrodo assunto come riferimento. L'elettrodo che si assume a questo fine come riferimento è l'elettrodo ad idrogeno standard caratterizzato da:
H3O+(aq) + e½ H2 (g) + nH2O
Il potenziale di un semielemento qualsiasi formato dalla coppia di ossidoriduzione O-R si identifica con la forza elettromotrice
della cella galvanica ottenuta accoppiando il semielemento considerato con l'elettrodo standard ad idrogeno:
Pt|H2 (g, 1 atm)|H3O+ (aq, aH3O+ = 1)||semielemento O,R
Il potenziale di un semielemento dipende dalle attività dei suoi componenti partecipanti al processo ossidoriduttivo che gli è
proprio: se esse sono unitarie, il potenziale si riduce al valore standard. Per la pila Daniell:
[-] Zn|Zn2+ (aq, aZn2+ = 1)||Cu2+ (aq, aCu2+ = 1)|Cu [+]
E=E°Cu2+/Cu - E°Zn2+/Zn = +0,337 - (-0,763) = 1,100 Volt
La serie dei potenziali standard è spesso designata col nome di serie elettrochimica.
Î
Î
Î
Ù
Interpretazione dei fenomeni elettrolitici
Quando agli elettrodi di una cella elettrolitica si applica una d.d.p. continua, si ha un passaggio di corrente attraverso la soluzione, ma la sua intensità è sensibile solo se la d.d.p. applicata agli elettrodi supera un determinato valore di soglia, variabile
seconda la natura dell'elettrolita, detto potenziale di decomposizione, mentre al di sotto di esso, l'intensità della corrente è trascurabile. Consideriamo nella cella una soluzione di HCl ed applichiamo agli elettrodi una d.d.p. molto piccola: non si osserva
alcuna reazione sugli elettrodi, tuttavia gli ioni H3O+ e Cl- si scaricano sulla loro superficie e le molecole H2 e Cl2 vi rimangono assorbite. Catodo ed anodo, da elettrodi inerti, originano una cella chimica:
Pt|H2 (g)|H3O+,Cl-(aq)|Cl2 (aq)|Pt
La sua f.e.m., che si oppone alla d.d.p. applicata dall'esterno agli elettrodi (detta forza controelettromotrice di polarizzazione
chimica degli elettrodi), aumenta a mano a mano che nuovi ioni H3O+ e Cl- si scaricano, aumentando l'attività dell'idrogeno e
95
del cloro assorbiti allo stato gassoso sugli elettrodi, fino a raggiungere il valore della d.d.p. imposta dall'esterno, annullandone
l'efficacia ed impedendo l'elettrolisi. Solo se la d.d.p. agli elettrodi supera la forza controelettromotrice massima, può prendere
il via l'elettrolisi. La curva dell'intensità di corrente in funzione della d.d.p. applicata (la idrolisi) mostra che anche al di sotto
del potenziale di decomposizione I non è nulla. Questa debole corrente, detta corrente di diffusione, deriva dal fatto che per
qualsiasi valore della d.d.p. applicata, un numero piccolo ma non nullo di molecole H2 e Cl2 assorbite dagli elettrodi si liberano
dalla loro superficie. L'eccedenza della effettiva d.d.p. che dà il via all'elettrolisi rispetto al potenziale termodinamico di decomposizione è detta sovratensione. La sua origine sta nel fatto che il processo di trasferimento degli elettroni dagli ioni in soluzione agli elettrodi è notevolmente lento e per essere attivato richiede un eccesso di energia.
Celle chimiche di uso comune e di interesse tecnico.
Le celle chimiche di pratico impiego si sogliono classificare in due categorie:
CELLE PRIMARIE
CELLE SECONDARIE
Una volta sfruttate come sorgenti di energia e quindi scaricate, non Possono essere ricaricate collegando gli elettrodi ad una adatta sorpossono essere restaurate nel loro stato originario per le alterazioni gente di d.d.p. continua, facendole così funzionare da celle elettrolitiche nelle quali vengono forzatamente invertiti i processi che vi
irreversibili che il processo di scarica vi determina.
si sono svolti durante la scarica.
1.
Pila a secco Leclanchè. Diffusa per il suo basso costo e le buone caratteristiche: E = 1,55 Volt. Formata da una bacchetta
di carbone (catodo +) immersa in una miscela umida di MnO2 e grafite in polvere, che a sua volta è circondata dall'elettrolita, costituita da una soluzione acquosa di NH4Cl. Il tutto è avvolto da un cilindretto di zinco (anodo -). Si ossida lo zinco
e si riduce il manganese:
Zn2+ + 2ereazione anodica: Zn
+
2NH3 + 2MnO (OH)
reazione catodica: 2NH4 + 2MnO2 + 2ePila a bottone Ruben-Mallory. Costituita da un dischetto di polvere compressa di grafite e HgO (polo +) e da un dischetto
di polvere di zinco compressa (polo -) separati da un terzo disco di materiale cellulosico imbevuto di KOH (ca.40%). Il
tutto è contenuto in un cilindro isolante chiuso a pressione da due dischi di acciaio: E = 1,34 Volt.
Zn(OH)2 + 2ereazione anodica: Zn + 2OH2OH- + Hg
reazione catodica: HgO + H2O + 2eBatteria piombo-acido solforico. Un singolo elemento ha E = 2,2 Volt: ogni elemento è costituito da un elettrodo di piombo spugnoso (polo -) e da un elettrodo di PbO2 pressato contro una griglia di piombo (polo +), entrambi immersi in una soluzione concentrata di acido solforico. Se la scarica viene prolungata troppo, il solfato di piombo si forma in grossi granuli
che non reagiscono più nel periodo di ricarica e l'accumulatore si deteriora (solfatazione).
PbSO4 (s) + nH2O + 2ereazione anodica: Pb(s) + SO42+ (aq)
+
2PbSO4 (s) + nH2O
reazione catodica: PbO2 (s) + 4H3O (aq) + SO4 (aq) + 2eAccumulatori alcalini al ferro-nichel. L'elettrodo positivo è costituito da ossidi di nichel mescolati con polvere dello stesso
metallo per rendere conduttrice la massa, compresi entro una griglia di acciaio. L'elettrodo negativo è costituito da ferro in
polvere compresso in una griglia analoga. L'elettrolita è una soluzione acquosa di idrossido di potassio. Sono molto resistenti ma assai costosi.
Î
2.
Î
Î
3.
Î
Î
4.
Î
Celle di concentrazione
Il valore del potenziale di un semielemento qualunque dipende dalle attività delle specie, ioniche e non ioniche, che partecipano
al processo ossidoriduttivo. Accoppiando due semielementi dello stesso tipo ma con concentrazioni diverse, si ottiene una cella
chimica la cui f.e.m. è regolata dalle concentrazioni stesse:
Cu|Cu2+ (aq, a1)||Cu2+(aq, a2)|Cu
E 1 = E o Cu 2+ +
Cu
E 2 = E o Cu2 + +
Cu
RT
ln a 1
2f
RT
ln a 2
2f
E 2 > E1 ⇒ E = E 2 − E 1
96
Cinetica chimica
Considerazioni introduttive
Ci sono reazioni che si compiono così rapidamente da essere giudicate istantanee, come molte reazioni tra ioni in soluzione.
Altre sono tanto lente da doversi concludere, in pratica, che non avvengano affatto: per esempio, se si mescolano H ed O a
temperatura ambiente, il sistema sembra del tutto inerte anche se dal punto di vista termodinamico la reazione
H2O è largamente favorita (∆G°298K = -55 Kcal/mol-1). La velocità con cui una reazione procede verso l'equiliH2 + ½O2
brio è influenzata da diversi fattori: concentrazione dei reagenti, temperatura, sostanze aggiunte (catalizzatori o inibitori).
Î
Velocità di reazione
La velocità di una reazione è definita dall'incremento del suo grado di avanzamento nell'unità di tempo:
vR =
∆ξ
∆ ξ dξ
⇒ v R = lim
=
∆
→
0
t
∆t
∆t
dt
Molto spesso si fa però riferimento alla velocità di trasferimento di una data specie reagente o alla velocità di formazione di un
dato prodotto, riferita al numero di moli che si trasformano nell'unità di tempo, riferita ad un volume unitario:
vi = ±
1 dni
V dt
Si assume il valore positivo se il componente i è un prodotto, negativo se è un reagente. Se il volume del sistema reagente è costante:
vi = ±
dc i
dni
⇒ dc i =
dt
VCOSTANTE
Essa è facilmente esprimibile in funzione della velocità di reazione essendo dni = vi dξ:
vi = ±
v i dξ
v
= ± i vR
V dt
V
Osserviamo che la velocità netta della reazione da sinistra a destra è data in ogni istante dalla differenza tra la reazione diretta e
la velocità della reazione inversa.
Velocità di reazione e concentrazione delle specie reagenti: equazioni cinetiche
La dipendenza funzionale della velocità di una reazione dalle concentrazioni delle specie reagenti è espressa dalla equazione
cinetica. Reazioni formalmente simili possono avere equazioni molto differenti:
H 2 + I 2 → 2 HI ⇒
dc HI
= kc H 2 c I 2
dt
1
k ′c H 2 c Br2 2
dc
H 2 + Br2 → 2 HBr ⇒ HBr =
c
dt
1 + k ′′ HBr
c Br2
Pur non essendo possibile ricondurre le equazioni cinetiche di reazioni diverse ad un unico modello, spesso, almeno nella fase
iniziale, la vR risulta direttamente proporzionale alle concentrazioni delle specie reagenti elevate ad opportuni esponenti. Per
lL + mM+ …:
aA + bB + …
Î
−
dc A
n
n
= kc A A c B B ....
dt
dove k è detta costante cinetica o velocità specifica. Quando una reazione corrisponde a questo modello, si dice che è di ordine
n = nA+nB+… Si dice ordine totale della reazione la somma degli esponenti a cui sono elevate le concentrazioni dei componenti. I singoli esponenti sono gli ordini parziali rispetto a ciascun componente. In genere, per reazioni semplici, che avvengono in
un unico stadio o che sono il risultato di un gran numero di processi elementari tutti identici, gli esponenti delle concentrazioni
nell'equazione cinetica coincidono con i coefficienti stechiometrici dei rispettivi componenti, mentre per reazioni complesse,
che si svolgono in più stadi con processi elementari differenti, essi spesso non coincidono.
97
1.
Reazioni del I ordine. Sono del I ordine molte reazioni di decomposizione termica, di isomerizzazione, decomposizione
elettrolitica in soluzione acquosa, decadimenti radioattivi. Per questo tipo di reazioni:
−
dc
= kc
dt
da cui si ottiene, dividendo le variabili:
c
−
t
dc
dc
c
= kdt ⇔ ∫
= ∫ − kdt ⇔ ln = − kt
c
c
c°
0
c°
c = c°e − kt
La quantità della specie reagente decresce esponenzialmente nel tempo:
c
c°
2.
t
Reazioni del II ordine. Come esempi abbiamo la decomposizione termica dell'acido iodidrico, l'idrolisi degli esteri in soluzione basica. L'equazione cinetica è del tipo:
−
dc A
dc
= − B = kc A c B
dt
dt
Nel caso in cui la specie reagente sia unica:
−
c
t
1 1
dc
dc
dc
= kc 2 ⇒ − 2 = kdt ⇔ − ∫ 2 = ∫ kdt ⇔ − = kt
dt
c c°
c
0
c° c
Determinazione sperimentale dell'equazione cinetica
Se la sua equazione è riducibile alla forma:
−
dc i
n
= kc i i
dt
L'esponente ni può essere determinato misurando il tempo necessario perché la concentrazione ci del componente si riduca alla
(semiperiodo). Questa espressione della equazione cinetica può essere tratta dalla generale
metà del suo valore iniziale c°i
quando il componente i sia nettamente in difetto rispetto agli altri. Se ni = 1:
ci
1 c1o/ 2
1 1 1
ln o = − kt ⇒ t 1 / 2 = − ln o = − ln = ln 2
k
k 2 k
ci
ci
Se invece ni = 2:
1
1
1 1
1  1 1
− o = kt ⇒ t 1 / 2 =  o − o  =
ci ci
k  c1 / 2 c i  k c io
Meccanismi di reazione. Il complesso attivato
Ogni reazione è il risultato di un numero straordinariamente grande di processi elementari nei quali le molecole dei reagenti si
trasformano in quelle dei prodotti o direttamente o attraverso una concatenazione di stadi successivi. Un meccanismo semplice
2HI. Un meccanismo complesso è, per esempio, la reazione tra perossido di idrogeno ed acido bromiè la reazione H2 + I2
Br2 + 2H2O il cui meccanismo si compone di due stadi successivi, in ognuno dei quali gli atti redrico H2O2 + 2H+ + 2Br attivi elementari sono collisioni di 3 particelle soltanto:
HOBr + H2O
Br2 + H2O
H+ + Br - + H2O2
HOBr + H+ + Br I singoli processi elementari che si svolgono a livello molecolare in una reazione semplice o in ogni stadio di una reazione
complessa vengono classificati in base alla loro molecolarità, cioè al numero di particelle che vi prendono parte (molecole, ioni
o radicali). In ogni atto reattivo elementare si ha la trasformazione di determinate specie reagenti in altre, e questa trasformazione si attua in ogni caso attraverso uno stato di transizione in cui le specie reagenti formano un complesso attivato, costituita
da una sola molecola, o da uno ione o da un radicale nei processi monomolecolari, da due e da tre molecole, ioni o radicali, in
quelli bi o trimolecolari: la molecolarità di un processo elementare corrisponde al numero di particelle reagenti che ne costituiscono il complesso attivato.
Î
98
Î
Î
Î
1.
Processi monomolecolari. Il complesso attivato è costituito da una molecola che si trova in uno stato energetico eccitato
per avere acquisito una certa quantità di energia in seguito agli urti con altre molecole o per assorbimento di radiazioni. La
molecola può così disattivarsi e tornare allo stato originario urtando altre molecole, oppure può decomporsi o trasformare
la propria struttura (cioè isomerizzarsi):
O3 + energia ⇔ O3 → O2 + O
ozono
2.
eccitato
Processi bi e trimolecolari. Il complesso attivato è un aggregato rispettivamente di due e di tre particelle reagenti di definita geometria: il complesso attivato, che è sempre un aggregato instabile, in seguito alle vibrazioni dei suoi atomi si decompone o rigenerando le molecole originarie o frazionandosi in specie diverse costituenti i prodotti finali del processo elementare considerato:
H 2 + I 2 ⇔ H 2 + I 2 → 2 HI
eccitato
Meccanismi di reazione ed equazioni cinetiche
L'equazione cinetica di una reazione è determinata dal meccanismo con cui essa procede. Per le reazioni semplici, ordine e molecolarità coincidono. Ciò è rigorosamente vero solo per i processi bi e trimolecolari. Quanto ai processi monomolecolari in
fase gassosa, non sono sempre del I ordine. Non vale l'inverso: non tutte le reazione del II ordine sono determinate da processi
elementari bimolecolari e non tutte quelle del III sono date da processi trimolecolari. Spesso, nella sequenza dei processi elementari di un meccanismo complesso ce n'è uno nettamente più lento degli altri, ed allora la vr complessiva è praticamente deC + D si svolga con un meccanismo a più stadi:
terminata dalla velocità di questo solo processo. 2A + B
E+F
stadio lento
A+B
G+H
A+E
F+G+H
C+D
stadi veloci
C+D
2A + B
allora si ottiene vr = k1 cA cB. Molte reazioni complesse sono caratterizzate da un meccanismo a catena in cui da principio
prendono origine delle specie altamente reattive (detti centri attivi) che successivamente reagiscono formando i prodotti finali
e, contemporaneamente, rigenerandosi in una prolungata sequenza di ripetuti e svariati processi elementari legati l'uno all'altro
come gli anelli di una catena. Tre tipi differenti di processi elementari concorrono al meccanismo di una reazione a catena:
• Innesco (o inizio della catena) in cui si originano i primi centri attivi, per eccitazione o per dissociazione delle specie reagenti.
• Propagazione della catena, serie più o meno lunga di processi in cui i centri attivi reagiscono e si rigenerano.
• Rottura della catena, in cui i centri attivi si neutralizzano a vicenda, ricombinandosi in molecole stabili o disattivandosi
per urto con altre molecole o con le pareti del recipiente.
Esempio:
Br + Br + M
innesco
Br2 + M
rottura
Br + Br + M
Br2 + M
HBr + H
Br + H2
HBr + Br
propagazione
H + Br2
H2 + Br
H + HBr
M è una qualsiasi molecola del sistema reagente che urta Br2 e lo scompone in 2Br.
Î
Î
Î
Î
Î
Î
Î
Î
Î
Î
L'equilibrio chimico dal punto di vista cinetico
Ogni reazione, in un sistema chiuso, è destinata a raggiungere uno stato di equilibrio che può essere più o meno prossimo ai
prodotti da essa risultanti o alle specie messe inizialmente a reagire e in ogni istante la velocità del progredire verso lo stato finale a cui tende è determinata dalla differenza delle velocità dei due sensi della reazione. Quando la velocità dei due processi
opposti si eguagliano, la reazione raggiunge lo stato di equilibrio: macroscopicamente non si osserva più alcuna trasformazione
del sistema, ma sul piano microscopico molecolare la reazione continua, nei due sensi contrari, con uguale velocità:
99
(k )
H 2 + I 2 ⇔ 2 HI
( k ')
dc HI
= kc H 2 c I 2
dt
dc
2
− HI = k ' c HI
dt
2
kc H 2 c I 2 = k ' c HI
2
c
k
= HI = k (T )
k' c H 2 c I2
che corrisponde alla espressione della legge termodinamica dell'equilibrio per la reazione.
Velocità di reazione e temperatura: teoria delle collisioni molecolari per le
reazioni tra gas
Consideriamo lo schema A + A
timetro cubo è:
Î prodotti. Il numero di urti bimolecolari che in un gas si verificano ogni secondo in un cenℵ AA = 2σ A
2
 πRT 


M
 A 
1/ 2
(n )
* 2
A
dove nA* è il numero di molecole di A in 1 cm3. Se ad ogni urto tra due molecole A queste si trasformassero nei prodotti, nell'unità di volume si trasformerebbero ogni secondo 2ℵAA molecole e quindi per la velocità di reazione si potrebbe porre:
dn *A
−
= 2ℵ AA
dt
ma un semplice calcolo orientativo porta a concludere diversamente: non tutte le collisioni tra le molecole della specie reagente
determinano la loro trasformazione nelle molecole dei prodotti, ma solo una piccolissima frazione:
(ℵAA)eff. = qeff. * ℵAA
dove qeff. È proprio il numero di collisioni efficaci, da cui :
dna*
−
= 2(ℵ AA )eff .
dt
Una prima fondamentale causa di limitazione del numero di urti
efficaci è suggerita dalla gran sensibilità della vr alle variazioni di
temperatura. Se il numero di collisioni nell'unità di tempo è poco
sensibile al variare della temperatura, considerando le curve di
distribuzione delle velocità molecolari in un gas, si rileva che essa influisce moltissimo sul numero di molecole che hanno un'energia cinetica superiore ad un certo minimo E*. Quindi possono
reagire, quando vengono in collisione tra loro, solo le molecole
con energia cinetica maggiore di un certo minimo. Perché due
molecole della specie reagente, venendo a contatto l'una con l'altra, possano formare il complesso attivato che condiziona l'attuarsi della reazione, è necessario che la forza viva dell'urto le
fornisca delle quantità di energia che il complesso attivato ha,
rispetto ad esse, in sovrappiù: questa quantità, uguale alla differenza tra l'energia del complesso attivato e l'energia delle molecole reagenti, è detta energia critica di attivazione della reazione
(Ea). Possono quindi risultare reattive soltanto le collisioni tra le molecole che abbiano, quando vengono a contatto l'una con
l'altra, un'energia cinetica relativa superiore ad Ea. Applicando la statistica di Maxwell-Boltzman:
ℵ AA (E a ) = ℵ AA e
−
Ea
RT
Però, affinché possa formarsi il complesso attivato, è anche necessario che le due molecole siano orientate, l'una rispetto all'altra, in maniera favorevole alla sua formazione. Di questa ulteriore causa di limitazione degli urti relativi, tiene conto il fattore
sterico (p), che rappresenta la probabilità che l'orientazione delle due molecole sia adatta alla formazione del complesso attivato. Tirando le somme:
100
(ℵ AA )eff
= pℵ AA (E a ) = pℵ AA e
−
Ea
RT
Quindi essendo (ℵAA)eff = qeff ℵAA:
qeff = pe
−
Ea
RT
e la velocità della reazione:
dn *
2  π RT 

− A = 2(ℵ AA )eff = p * 4σ A 
dt
 MA 
Confrontando questo risultato con l'equazione cinetica sperimentale
−
1/ 2
e
−
Ea
RT
(n )
* 2
A
n*
dc A
2
= kc A , tenendo conto che c A = A 10 3 , si
dt
N
deduce che:
k = p * 4σ A
−
2
N
10 3
 πRT 


 MA 
1/ 2
e
−
Ea
RT
Ea
RT
A tale riguardo due sono i fattori che giocano: e
, di peso determinante, e T½, la cui sensibilità al variare di T è di poco
conto. Trascurando questo secondo fattore, così da poterlo raccogliere con tutte le altre quantità indipendenti dalla temperatura
in un'unica costante Z:
k = Ze
−
Ea
RT
nota come equazione di Arrhenius. Come conseguenza, le reazioni caratterizzate da un'elevata energia di attivazione possono
svolgersi con velocità apprezzabile solo a temperature sufficientemente alte. È per questa ragione che molte reazioni, pur essendo termodinamicamente favorite, appaiono in realtà del tutto inibite alle normali temperature.
101
Catalisi
Generalità
Si dà il nome di catalizzatore a qualsiasi sostanza capace di influire con la propria presenza sulla velocità di una reazione, senza tuttavia venire trasformata. I catalizzatori possono essere di due tipi: positivi se accelerano le razioni o negativi (o inibitori)
se la ritardano. Si parla poi di catalisi omogenea se il catalizzatore fa parte della stessa fase (gassosa o soluzione) in cui si trovano le specie reagenti. Se il catalizzatore e le specie reagenti costituiscono fasi distinte, si parlerà di catalisi eterogenea. Per
tutti i processi catalitici si riscontrano le seguenti caratteristiche:
1. L'azione catalitica è esclusivamente cinetica; non possono essere promosse reazioni termodinamicamente inibite.
2. La presenza di un catalizzatore in un sistema chimico in reazione non altera la posizione dell'equilibrio a cui il sistema tende, ma influisce solo sulla velocità con cui l'equilibrio viene raggiunto.
3. Ogni catalizzatore presente in un sistema chimico in reazione, pur non influendo sulla stechiometria del processo, partecipa
alla formazione dei complessi attivati.
4. Quando le specie reagenti possono trasformarsi in diversi processi paralleli, il catalizzatore esplica un'azione selettiva.
5. Quantità molto piccole di catalizzatore bastano per attivare la reazione di grandi quantità di specie reagenti.
Catalisi omogenea
Meccanismi di catalisi omogenea sono frequenti in fase gassosa o in soluzione: nelle reazioni non implicanti processi a catena,
la velocità risulta di regola proporzionale alla concentrazione del catalizzatore. Questo lo schema generale: il catalizzatore forma con le specie reagenti uno o più prodotti intermedi con energia di attivazione più bassa di quella caratterizzante la reazione
diretta fra le specie medesime in assenza di catalizzatore e da essi si originano successivamente i prodotti finali.
SO2 + ½ O2
SO3, senza catalizzatori questa è una reazione molto lenta. Con NO la reazione procede attraverso due stadi
NO2 , NO2 + SO2
SO3 + NO.
con Ea nettamente più bassa: ½ O2 + NO
In soluzione la forma più comune di catalisi omogenea è la catalisi acido-basica, nella quale intervengono come catalizzatori
gli ioni H3O+ e OH- (specifica) o altri acidi ed altre basi (generale).
Ù
Î
Î
Catalisi eterogenea
Nella catalisi eterogenea, o di contatto, le specie reagenti si trovano nella fase fluida ed il catalizzatore è un solido. La reazione
avviene sulla sua superficie: le molecole reagenti, urtandola, vi si fissano nei punti di maggior reattività (centri attivi) e nel legarsi subiscono un riordinamento elettronico che facilita la reazione indebolendo particolarmente determinati legami. Questo
fenomeno è detto assorbimento. L'energica interazione tra le molecole assorbite e la superficie del catalizzatore solido si definisce chemiassorbimento (in quanto si verificano veri e propri legami chimici) per distinguerla dall'assorbimento fisico determinato da deboli forze di Van der Waals (come ad esempio l'assorbimento dell'acqua da parte di una spugna, durante il quale
non avviene alcun legame chimico). Le molecole presenti nella fase fluida a contatto con la superficie del catalizzatore si fissano nei punti più aggredibili, i centri attivi: essi corrispondono ad atomi particolarmente insaturi per i difetti reticolari. L'addizione al catalizzatore di tracce di adatte sostanze (promotori) può aumentare considerevolmente il numero di centri attivi, esaltando la catalisi. L'attività di un catalizzatore solido può essere distrutta se esso viene portato a temperatura troppo alta: a fenomeni di questo tipo di ricristallizzazione è dovuto l'invecchiamento dei catalizzatori solidi. L'attività catalitica può essere ridotta o annullata anche dall'assorbimento di date sostanze (veleni) che possono agire o bloccando i centri attivi o avviando reazioni diverse da quella voluta. La quantità di sostanza assorbita è funzione della sua concentrazione nella fase fluida a contatto:
aumenta con essa e tende asintoticamente ad un valore limite costante che corrisponde alla saturazione totale dei centri attivi
superficiali. La velocità del processo di assorbimento (vad) è proporzionale alla concentrazione delle molecole del gas e quindi
alla pressione ed al numero di centri attivi (1-ϑ). Indichiamo con ϑ il grado di ricoprimento:
v ad = k ad P (1 − ϑ ) 

v de = k deϑ
v ad = v de
k ad P (1 − ϑ ) = k deϑ 
k ad
P
k ad P
k de
k
kP
ϑ=
=
=
⇒ k = ad
k
1 + kP
k de + k ad P
k de
1 + ad P
k de
102