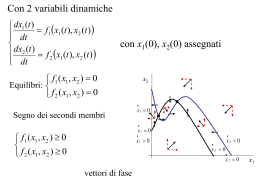
Con 2 variabili dinamiche
 dx1 (t )
 dt  f1 x1 (t ), x2 (t ) 

 dx2 (t )  f  x (t ), x (t ) 
2 1
2
 dt
con x1(0), x2(0) assegnati
 f1 ( x1 , x2 )  0
Equilibri: 
 f 2 ( x1 , x2 )  0
x2

Segno dei secondi membri
x1  0

x1  0
 f1 ( x1 , x2 )  0

 f 2 ( x1 , x2 )  0

x1  0


x2  0
x2  0

x2  0
vettori di fase
x1
Preda-predatore (Vito Volterra, 1926)

Densità prede
x 1  r x1  b x1x2
x1

x 2   m x2 + c x1x2
Densità predatori x2

x 1  x1 (r  b x2)  0

x 2  x2( m + c x1)  0
x2

x1  0

x1  0

x1  0


x2  0 x2  0

x2  0
x1
Vito Volterra (1860-1940)
Il matematico si trova in possesso di uno strumento
mirabile e prezioso, creato dagli sforzi accumulati
per lungo andare di secoli dagli ingegni più acuti
e dalle menti più sublimi che siano mai vissute.
Egli ha, per così dire, la chiave che può aprire il
varco a molti oscuri misteri dell’universo, ed un
mezzo per riassumere in pochi simboli una sintesi
che abbraccia e collega vasti e disparati risultati di
scienze diverse
Vito Volterra (1860-1940)
[…]
Ma è intorno a quelle scienze nelle quali le matematiche solo da poco tempo
hanno tentato d’introdursi, le scienze biologiche e sociali, che è più intensa
la curiosità, giacché è forte il desiderio di assicurarsi se i metodi classici, i
quali hanno dato così grandi risultati nelle scienze meccanico-fisiche, sono
suscettibili di essere trasportati con pari successo nei nuovi ed inesplorati
campi che si dischiudono loro dinanzi.
dal discorso inaugurale per l’anno accademico 1901-1902 dell’Università di Roma
"Plasmare dunque concetti in modo da poter
introdurre la misura; misurare quindi; dedurre
poi delle leggi; risalire da esse ad ipotesi; dedurre
da queste, mercé l'analisi, una scienza di enti
ideali si, ma rigorosamente logica; confrontare
poscia con la realtà; rigettare o trasformare, man
mano che nascono contraddizioni tra i risultati
del calcolo ed il mondo reale, le ipotesi
fondamentali che han già servito; e giungere così
a divinare fatti e analogie nuove, o dallo stato
presente arrivare ad argomentare quale fu il
passato e che cosa sarà l'avvenire; ecco, nei più
brevi termini possibili, riassunto il nascere e
l'evolversi di una scienza avente carattere
matematico.“
Vito Volterra, Saggi Scientifici, Zanichelli Bologna
1920
Y
E
X
Fluttuazioni del numero di lepri e linci canadesi ricostruite in base al numero delle pelli
acquistate dalla Compagnia della Baia di Hudson nei diversi anni, da Mac Lulich (1937)

x1  r x1  sx12  x1x2 = x1(rsx1bx2)

x 2   m x2 + c x1x2 = x2(m+cx1)
Predatori x2
Crescita logistica della preda
Prede x1
Predatori x2
4
3
2
1
tempo
1
2
Prede x1
Sazietà del predatore

b
bx2 

x1  rx1  sx 
x1 x2  x1  r  sx1 
a  x1
a  x1 


2
1

c
cx1 


x 2  mx2 
x1 x2  x2   m 
a  x1
a  x1 


(a) Lotka-Volterra senza classico
senza smorzatore per la preda
(b) Con smorzatore per la preda
(c) Con saturazione dell’appetito
Modelli lineari a tempo continuo bidimensionali
 dX 1 (t )
 dt  a11 X 1 (t )  a12 X 2 (t )

 dX 2 (t )  a X (t )  a X (t )
21 1
22 2
 dt
Sol. di prova
X 1  w1et
X 2  w2et
w1et  a11w1et  a12 w2et
Sostituisco
w2et  a21w1et  a22 w2et
(a11   ) w1  a12 w2  0
a21w1  (a22   ) w2  0
Ha soluzioni non nulle se
cioè
Sistema lineare omogeneo con parametro
(equazione agli autovalori)
(a11   )(a22   )  a12a21  0
2  (a11  a22 )  (a11a22  a12a21 )  0
  Tr  Det  0
2
= a11 a22 a12 a21
Tr2  4det = 0
= a11 + a22
(1) Due radici 1,2 (autovalori) reali distinte
con corrispondenti autovettori v1 e v2
Tr2  4Det >0
Soluzione generale:
X(t) = C1 v1e 1t +C2 v2 e 2t
(2) Due radici 1,2 (autovalori) reali
coincidenti
Tr2  4Det = 0
e t
Soluzione generale:
X(t) = v (C1 +C2t)
(3) Due radici 1,2 (autovalori) complesse
coniugate: Tr2  4Det < 0
1  a +ib 2  a  ib
Soluzione generale:
S.D.
 dx1 (t )
 dt  f1 x1 (t ), x2 (t ) 

 dx2 (t )  f  x (t ), x (t ) 
2 1
2
 dt
 f1 ( x1 , x2 )  0
Equilibri: 
 f 2 ( x1 , x2 )  0
f i
aij 
|( p ,q )
x j
con x1(0), x2(0) assegnati
Stabilità di ciascun equilibrio.
Approssimazione lineare in un intorno.
Sia (x1*, x2*) un equilibrio, dette X1 = x1 x1*, X2 = x2 x2* si introduce
l’approssimazione lineare in un intorno dell’equilibrio calcolando in esso le 4
derivate parziali:
Matrice Jacobiana aij 
f i
x j
Calcolata in un punto di equilibrio
Approx. lineare
 dX 1 (t )
 dt  a11 X 1 (t )  a12 X 2 (t )

 dX 2 (t )  a X (t )  a X (t )
21 1
22 2
 dt
Esempio
Cont. esempio
Esempi
Competizione fra due specie


x1  r1 x1  s1 x12  12 x1 x2  x1 r1  s1 x1  12 x2



x 2  r2 x2  s x  12 x1 x2  x2 r2  s2 x2  12 x1
2
2 2

Gli esperimenti di Gause (1934)
due specie di protozoi: Paramecium aurelia e Paramecium caudatum.
Ponendo in colture separate le due specie, e rinnovando periodicamente il terreno, si
ottennero curve di accrescimento approssimativamente sigmoidali con il conseguimento
d’uno stato stazionario. Ponendo le due specie insieme in uno stesso terreno di coltura
si vide che mentre Paramecium aurelia manteneva ancora un accrescimento logistico,
la popolazione di Paramecium caudatum, dopo un certo numero di giorni (circa 8),
cominciò a diminuire fino a scomparire del tutto. Da ciò si può dedurre che una delle
due specie è riuscita a competere meglio per le risorse causando l’estinzione di quella
concorrente.
Il principio d’esclusione competitiva (principio di Gause).
Se due specie coesistono in un medesimo ambiente ciò avviene in ragione del fatto che
esse presentano nicchie ecologiche separate. Qualora, però, le due specie presentino
nicchie sovrapposte, allora una delle due specie prenderà il sopravvento sull’altra fino
ad eliminarla.
Comunque, spesso la coesistenza è garantita dalla presenza di nicchie ecologiche non
completamente sovrapposte (le specie in questioni possono presentare, infatti,
differenze lievi a livello di dieta o di habitat). In conseguenza di ciò nasce il quesito su
quanto due nicchie debbano essere separate affinché la coesistenza sia permessa..
Edward Lorenz
(May 23, 1917–April 16, 2008)
dx
 x  y
dt
dy
 Rx  y  xz
dt
dz
  Bz  xy
dt