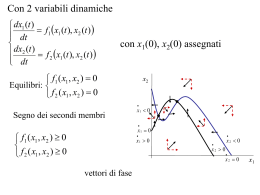
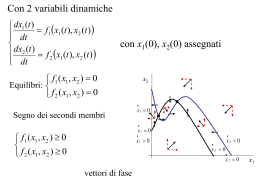
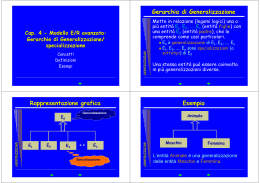
Metodo di sostituzione
4x + 2y = 5
3x - y = 1
Metodo di sostituzione
4x + 2y = 5
3x - y = 1
Metodo di sostituzione
4x + 2y = 5
3x - y = 1
y = 3x - 1
Metodo di sostituzione
4x + 2y = 5
3x - y = 1
y = 3x - 1
Metodo di sostituzione
4x + 2y = 5
3x - y = 1
y = 3x - 1
Metodo di sostituzione
4x + 2y = 5
3x - y = 1
y = 3x - 1
Metodo di sostituzione
4x + 2(3x – 1) = 5
y = 3x - 1
Metodo di sostituzione
4x + 2(3x – 1) = 5
y = 3x - 1
4x + 6x = 5 + 2
Metodo di sostituzione
4x + 2(3x – 1) = 5
y = 3x - 1
4x + 6x = 5 + 2
x = 7/ 10
Metodo di sostituzione
4x + 2(3x – 1) = 5
y = 3x - 1
x = 7/ 10
Metodo di sostituzione
4x + 2(3x – 1) = 5
y = 3x - 1
x = 7/ 10
Metodo di sostituzione
x = 7/ 10
y = 3(7/10) - 1
11
y=
10
SOLUZIONE:
7
x=
10
11
y=
10
Metodo del confronto
4x + 2y = 5
3x - y = 1
Metodo del confronto
4x + 2y = 5
3x - y = 1
Metodo del confronto
y = -2x + 5/2
y = 3x - 1
Metodo del confronto
y = -2x + 5/2
y = 3x - 1
-2x + 5/2 = 3x - 1
-5x = -7/2
x=
7
10
Metodo del confronto
4x + 2y = 5
3x - y = 1
Metodo del confronto
4x + 2y = 5
3x - y = 1
Metodo del confronto
x = -1/2y + 5/4
x = 1/3y + 1/3
Metodo del confronto
x = -1/2y + 5/4
x = 1/3y + 1/3
-1/2y + 5/4 = 1/3y + 1/3
-5/6y = -11/12
y=
11
10
SOLUZIONE:
7
x=
10
11
y=
10
Metodo di riduzione
-2•
2x + 3y = 4
4x – 5y = - 1
Metodo di riduzione
-2•
-4x - 6y = -8
4x – 5y = - 1
0 –11y = -9
9
y=
11
+
Metodo di riduzione
5•
2x + 3y = 4
3•
4x – 5y = - 1
Metodo di riduzione
5•
10x +15y = 20
3•
12x –15y = -3
22x + 0 = 17
17
x=
22
+
SOLUZIONE:
17
x=
22
9
y=
11
Metodo di Cramer
PREMESSA
a11 a12
A=
a21 a22
MATRICE
PREMESSA
a11 a12
A=
a21 a22
MATRICE
diagonale
principale
PREMESSA
a11 a12
A=
a21 a22
diagonale
secondaria
MATRICE
PREMESSA
a11 a12
A=
a21 a22
MATRICE
DETERMINANTE DELLA MATRICE A:
a11 a12
det(A) =
=
a21 a22
= a11 •a22 - a12 •a21
Metodo di Cramer
2x + 3y = 4
x – 5y = - 1
=
Metodo di Cramer
2x + 3y = 4
x – 5y = - 1
=
2
Metodo di Cramer
2x + 3y = 4
x – 5y = - 1
=
2
3
Metodo di Cramer
2x + 3y = 4
1x – 5y = - 1
2
=
1
3
Metodo di Cramer
2x + 3y = 4
x – 5y = - 1
2
=
1
3
-5
Metodo di Cramer
2x + 3y = 4
x – 5y = - 1
2
=
1
3 2•(-5)
= -13 - 3•1
-5
Metodo di Cramer
2x + 3y = 4
x – 5y = - 1
4
x =
-1
3 -17
= 4•(-5) - 3•(-1)
-5
Metodo di Cramer
2x + 3y = 4
x – 5y = - 1
2
y =
1
4 -6
= 2•(-1) - 4•1
-1
SOLUZIONE:
x
-17
17
x=
=
=
-13
13

-6
y
6
y=
=
=
-13
13
