Università degli Studi di Padova
CICLO DI LEZIONI “SCIENZE DI BASE” PER I DOTTORATI
DI RICERCA DELL’AREA MEDICA
Anno accademico 2005-06
Temi di Statistica ed Epidemiologia
PROBABILITÀ E DECISIONI IN MEDICINA:
I TEST DIAGNOSTICI
Francesco Grigoletto
Obiettivi
• Saper valutare l’accuratezza dei test di screening
• Utilizzare i risultati dei test diagnostici nell’assumere
decisioni riguardo alla gestione di uno specifico paziente
Programma
• Definizione e princìpi delle probabilità
• Uso di test di screening: sensibilità e specificità. Curve
ROC.
• Uso di test diagnostici: valore predittivo positivo e
negativo.
• Il teorema di Bayes.
La valutazione dei test
diagnostici e prognostici
• I test diagnostici predicono la presenza o
assenza di una malattia
• I test prognostici predicono l’esito di una
malattia
Caratteristiche di un test
diagnostico ideale
TEST
+
-
• Veloce
• Sicuro
• Semplice
• Indolore
• Affidabile
• Economico
CONDIZIONE
+
a
0
0
d
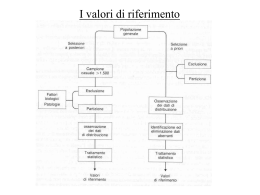
Struttura di uno studio sui test
diagnostici (1)
Come negli studi osservazionali:
– Variabile predittiva
Risultato del test
Qualitativo dicotomico/categoriale
Quantitativo discreto/continuo
– Variabile di esito Presenza/Assenza della
malattia (determinata da un
“gold standard”)
Struttura di uno studio sui test
diagnostici (2)
• Studi osservazionali informazione
sull’eziologia della malattia mostrando
un’associazione tra variabile predittiva e
malattia
• Studi sui test diagnostici quanto bene un
test può discriminare tra malati e sani
Sensibilità e specificità (1)
CONDIZIONE
+
TEST
TOTALE
+
-
VERI POSITIVI
(VP)
FALSI
NEGATIVI
(FN)
FALSI POSITIVI
(FP)
VP+FN
VERI NEGATIVI
(VN)
FP+VN
Sensibilità e specificità (2)
• Sensibilità quanto buono è il test nell’identificare
i malati: P(T+ M+)
Se =
VP
VP + FN
• Specificità quanto buono è il test nell’identificare
i sani: P(T- M-)
Sp =
VN
VN + FP
Sensibilità e specificità (3)
Relazione tra sensibilità e specificità:
• più sensibile è un test, minore sarà il numero di falsi
negativi, ciò è importante per una malattia grave e
rara come la fenilchetonuria;
• più specifico è un test, minore sarà il numero di falsi
positivi, ciò è importante per una malattia diffusa
come il diabete.
Esempio: potere discriminatorio
del test
CONDIZIONE
TUMORE AL
SENO
NODULO
BENIGNO
+
65
30
-
35
70
100
100
TEST
TOTALE
65
Sensibilità =
= 65%
65 + 35
70
Specificità =
= 70%
30 + 70
Esempio: sensibilità e specificità (1)
LIVELLO DI
GLUCOSIO
110 mg/100 ml
classificati diabetici
< 110 mg/100 ml
classificati non diab.
TOTALE
65
= 92,9%
70
247
SPECIFICITÀ =
= 48,4%
510
SENSIBILITÀ =
DIABETICI
NON
DIABETICI
TOTALE
65
263
328
5
247
252
70
510
580
Esempio: sensibilità e specificità (2)
LIVELLO DI
GLUCOSIO
130 mg/100 ml
classificati diabetici
< 130 mg/100 ml
classificati non diab.
TOTALE
57
= 81,4%
70
420
SPECIFICITÀ =
= 82,4%
510
SENSIBILITÀ =
DIABETICI
NON
DIABETICI
TOTALE
57
90
147
13
420
433
70
510
580
Esempio: sensibilità e specificità (3)
LIVELLO DI GLUCOSIO
NEL SANGUE (mg/100 ml)
SENSIBILITÀ
SPECIFICITÀ
80
100,0
1,2
90
98,6
7,3
100
97,1
25,3
110
92,9
48,4
120
88,6
68,2
130
81,4
82,4
140
74,3
91,2
150
64,3
96,1
160
55,7
98,6
170
52,9
99,6
180
50,0
99,8
190
44,3
99,8
200
37,1
100,0
A.
DIABETICI
NORMALI
N
D
Frequenza relativa
FASI POSITIVI
MASSIMA SENSIBILIT À
80
Livello di glucosio (mg/dl)
B.
NORMALI
D
Frequenza relativa
N
DIABETICI
ERRORE MINIMO
FASI NEGATIVI
FASI POSITIVI
130
Livello di glucosio (mg/dl)
C.
NORMALI
DIABETICI
D
Frequenza relativa
N
À
MASSIMA SPECIFICIT
FASI NEGATIVI
200
Livello di glucosio (mg/dl)
Scelta di un valore soglia
(punto di cutoff) (1)
• Molti test diagnostici danno una risposta di
tipo continuo e quindi deve essere presa una
decisione sul valore soglia che indica un
risultato positivo del test
• La scelta implica un aumento della
sensibilità a scapito della specificità e
viceversa
Scelta di un valore soglia
(punto di cutoff) (2)
Implicazioni della scelta:
– se si deve evitare un risultato FP (es.: il risultato serve
per decidere se un paziente deve essere sottoposto ad
un’operazione pericolosa), il valore soglia deve essere
scelto in modo da massimizzare la specificità del test;
– se si deve evitare un risultato FN (es.: screening per la
fenilchetonuria neonatale), il valore soglia deve essere
scelto in modo da massimizzare la sensibilità del test.
Scala TRISS
(Probabilità di decesso)
ESITO
TRISS
MORTO
+ ( 0,5)
- (< 0,5)
TOTALE
28
= 82,4%
34
68
SPECIFICIT À =
= 98,6%
69
28
VP + =
= 96,6%
29
SENSIBILIT À =
28
6
34
VIVO
TOTALE
1
68
69
29
74
103
Scala TRISS
(Probabilità di decesso)
ESITO
TRISS
MORTO
VIVO
TOTALE
+ ( 0,4)
29
2
31
- (< 0,4)
5
67
72
34
69
103
TOTALE
29
SENSIBILIT À =
= 85,3%
34
67
SPECIFICIT À =
= 97,1%
69
29
VP + =
= 93,5%
31
Scala SAPS II
(Probabilità di decesso)
ESITO
SAPS II
MORTO
VIVO
TOTALE
+ ( 0,5)
19
2
21
- (< 0,5)
13
67
80
TOTALE
32
69
101
19
= 59,4%
32
67
SPECIFICIT À =
= 97,1%
69
19
VP + =
= 90,5%
21
SENSIBILIT À =
Scala SAPS II
(Probabilità di decesso)
ESITO
SAPS II
MORTO
VIVO
TOTALE
+ ( 0,4)
21
3
24
- (< 0,4)
11
66
77
TOTALE
32
69
101
21
= 65,6%
32
66
SPECIFICIT À =
= 95,7%
69
21
VP + =
= 87,5%
24
SENSIBILIT À =
Scala APACHE III
(Probabilità di decesso)
ESITO
APACHE III
MORTO
VIVO
TOTALE
+ ( 0,5)
15
1
16
- (< 0,5)
9
68
77
24
69
93
TOTALE
15
= 62,5%
24
68
SPECIFICITÀ =
= 98,6%
69
15
VP + =
= 93,8%
16
SENSIBILITÀ =
Scala APACHE III
(Probabilità di decesso)
ESITO
APACHE III
MORTO
VIVO
TOTALE
+ ( 0,4)
19
1
20
- (< 0,4)
5
68
73
24
69
93
TOTALE
19
= 79,2%
24
68
SPECIFICIT À =
= 98,6%
69
19
VP + =
= 95,0%
20
SENSIBILIT À =
Le curve ROC
(Receiver Operating Characteristic)
• Un altro modo per stabilire il punto di cutoff è
attraverso la curva ROC: grafico della
sensibilità in funzione della proporzione di
falsi positivi (1-specificità)
• Il test ideale è quello che si situa all’angolo
superiore sinistro del grafico (100% sensibilità
e specificità)
Curva ROC (Receiver Operating Characteristic) di uno studio
per stabilire il miglior valore soglia (cut-off) per un programma
di screening per l’ipertensione (dati fittizi)
100
120 mmHg
130 mmHg
80
Sensibiità
140 mmHg
60
150 mmHg
40
160 mmHg
20
0
0
20
40
60
80
% Falsi positivi (100 - Specificità)
100
Esempi di curve ROC (Receiver Operating Characteristic) per
quattro test
100
Sensibiità
80
60
40
Curva di nessuna utilità
Curva discreta
20
Curva buona
Curva eccellente
0
0
20
40
60
80
% Falsi positivi (100 - Specificità)
100
Ruolo della prevalenza
Il valore di un test diagnostico dipende da:
– sensibilità,
– specificità,
– prevalenza.
• Al diminuire della prevalenza diminuisce la probabilità che
un soggetto con test positivo abbia la malattia e aumenta la
probabilità che il test rappresenti un falso positivo. Più rara
è la malattia (es.: tumore del colon in adulti asintomatici)
più specifico dovrà essere il test per essere clinicamente
utile.
• Se una malattia è comune (es.: malattia cardiaca in fumatori
di mezza età con l’angina), il test dovrà essere molto
sensibile per essere clinicamente utile.
I FENOMENI PROBABILISTICI
Alcune definizioni
PROBABILITÀ:
RAPPORTO
TRA
NUMERO
DI
CASI
FAVOREVOLI E NUMERO DI CASI POSSIBILI
(PURCHÉ TUTTI EGUALMENTE POSSIBILI)
ESPERIMENTO:
UNA QUALSIASI OPERAZIONE IL CUI
RISULTATO NON PUÒ ESSERE PREVISTO CON
CERTEZZA
EVENTO:
OGNI
POSSIBILE
ESPERIMENTO
SPAZIO DEGLI EVENTI:
INSIEME DI TUTTI GLI EVENTI POSSIBILI
(SPAZIO CAMPIONARIO)
RISULTATO
DI
UN
Esempio di esperimento: LANCIO DI UN DADO
SPAZIO DEGLI EVENTI:
{ 1, 2, 3, 4, 5, 6 }
EVENTO A = Uscita di un numero PARI
EVENTI ELEMENTARI:
A1 = Uscita di 2
A2 = Uscita di 4
A3 = Uscita di 6
A = A1
POICHÉ:
A1
A2
A1
A2
A1
A2
=
A2
A3
(= insieme vuoto)
SI DICE CHE A1, A2 e A3 SONO EVENTI A DUE A DUE INCOMPATIBILI
Operazioni sugli eventi
Unione
A
A
Intersezione
A
B
B (leggi: A o B)
B
A
Eventi incompatibili
A
A
B
B=
(insieme vuoto)
B (leggi: A e B)
1. Principio delle probabilità totali
Dati due eventi incompatibili A e B, di probabilità rispettivamente P(A) e
P(B), la probabilità che si verifichi l’uno o l’altro è data dalla somma delle
rispettive probabilità, ossia:
P(A
A
B) = P(A) + P(B)
B
Nell’esempio del dado:
P(A) = P(A1
A2
A3) = P(A1) + P(A2) + P(A3) =
=
1
6
+
1
+
6
1
6
=
Se gli eventi A e B sono compatibili, allora:
P(A
A
B
B) = P(A) + P(B) – P(A
B)
1
2
Esempio: Scelta di una carta da un mazzo di 52 carte
A = estrazione di un asso
P(A) =
4
52
B = estrazione di una carta di cuori
P(B) =
13
52
A
B = asso di cuori
Essendo
P(A
1
B) =
52
si ha che:
P(A
B) = P(A) + P(B) – P(A
=
4
13
+ 52
52
1
- 52
B) =
=
16
52
=
4
13
INDIPENDENZA
Definizione
Due eventi compatibili A e B si dicono indipendenti se
il verificarsi dell’uno non altera la probabilità del
verificarsi dell’altro, ossia
P(B) = P(B A)
(leggi: probabilità di B condizionata al verificarsi di A)
Esempio
URNA 1
A = estrazione di pallina rossa da URNA 1
B = estrazione di pallina rossa da URNA 2
P(A) =
6
01
URNA 2
(Gli eventi A e B sono compatibili
e indipendenti)
P(B) =
8
21
2. Principio delle probabilità composte
Dati gli eventi A e B indipendenti, la probabilità del loro verificarsi
congiunto è data dal prodotto delle rispettive probabilità, ossia:
P(A
B) = P(A) × P(B)
Nell’esempio dell’estrazione di una pallina rossa da ciascuna urna:
P(A
B) =
6 × 8
10
12
=
48
120
= 2
5
Il principio si può estendere al caso di più di due eventi compatibili.
DIPENDENZA
Definizione
Due eventi compatibili A e B si dicono dipendenti se il
verificarsi dell’uno altera la probabilità del verificarsi
dell’altro, ossia:
P(B A)
P(B A)
(leggi: probabilità di B condizionata
al non verificarsi di A)
Esempio
URNA 1
A = estrazione di pallina bianca da URNA 1
B = estrazione di pallina bianca dalla stessa URNA 1 (senza che
la prima pallina estratta sia reinserita nell’urna)
Gli eventi A e B sono dipendenti, poiché il risultato della prima estrazione altera la
probabilità dell’evento B. Infatti:
P(A) =
4
01
P(B A) =
3
9
P(B A) =
4
9
2. Principio delle probabilità composte (eventi dipendenti)
Dati gli eventi A e B dipendenti tra loro, la probabilità del loro
verificarsi congiunto è data dal prodotto della probabilità del
verificarsi di A per la probabilità condizionata P(B A) , ossia:
P(A
B) = P(A) × P(B A)
Nell’esempio dell’estrazione di una pallina rossa da ciascuna urna:
P(A
B) =
4 ×
10
3
9
=
12
90
In generale, si può anche scrivere:
P(A
B) = P(B) × P(A B)
= 2
15
Prevalenza e probabilità a
priori
• In un singolo paziente:
Prevalenza = Probabilità a priori
la probabilità, basata su caratteristiche
demografiche e cliniche, che un paziente
abbia la malattia prima di effettuare il test.
Esempio: probabilità condizionata
Qual è la probabilità che un soggetto
sopravviva per i successivi 5 anni (B), dato
che ha già raggiunto i 60 anni (A)?
Sapendo che:
P(A)=P(vivo a 60 anni)=0,85
P(A B)=P(vivo a 65 anni)=0,79
Allora:
P(B A)=0,79/0,85=0,93
Principio delle probabilità composte
B) = P(A | B) • P(B) = P(B | A) • P(A)
P(A | B) = P(B | A) • P(A) / P(B)
P(A
A = M+ (malformazione presente)
B = T+ (test positivo)
Teorema di Bayes
Sensibilità
VP+
(
+
PM |T
+
)
essendo :
( )
(
(
) ( )
( )
Prob. a priori
P T + | M+ • P M+
=
P T+
) ( ) (
) ( )
P T+ = P T+ |M+ • P M+ + P T+ | M • P M
Valore predittivo di un test (probabilità a
posteriori): teorema di Bayes
• Valore predittivo di un test positivo (VP+) =
Probabilità che una persona con un valore positivo
del test abbia la malattia
{
}
VP + = P M + T + =
Se × Prob. a priori
Se × Prob. a priori + (1 - Sp) × (1 Prob. a priori)
• Valore predittivo di un test negativo (VP-) =
Probabilità che una persona con un valore negativo
del test non abbia la malattia
{
VP = P M T
}= Sp × (1
Sp × (1 Prob. a priori)
Prob. a priori) + (1 - Se) × Prob. a priori
Problema
Dati:
• donna di 27 anni,
• alla 17ª settimana di gestazione,
• sofferente da 5 anni di diabete mellito insulino-dipendente,
• con controllo inadeguato della glicemia nel primo trimestre di gravidanza.
Dalla letteratura:
• c’è un rischio pari al 20% che il feto abbia malformazioni,
Risultato del test:
• positivo per l’alfa-feto-proteina nel siero materno (MSAFP)
Caratteristiche del test:
• sensibilità=34%
• specificità=86%
Qual è la probabilità che il feto abbia malformazioni?
( procedere con un ulteriore esame?)
M+ = 20%
Prima del test:
M- = 80%
Risposta
Se il test è positivo, la probabilità che il feto sia anormale è data
da:
6,8 %
P (M + | T + ) =
= 37,8%
18%
Se il test è negativo, la probabilità che il feto sia normale è data
da:
(
PM |T
)
68,8%
=
= 83,9%
82%
Esempio: valore predittivo di un test con sensibilità 90% e
specificità 90% per vari valori della probabilità a priori
della malattia
Probabilità a priori di
una malattia
VP+
VP-
0,001
0,01
0,9999
0,01
0,08
0,999
0,05
0,32
0,994
0,10
0,50
0,99
0,20
0,69
0,97
0,50
0,90
0,90
0,80
0,97
0,69
0,90
0,99
0,50
0,95
0,994
0,32
0,99
0,999
0,08
0,999
0,9999
0,01
Suscettibilità degli studi sui test diagnostici
ad errori casuali (1)
• Per effetto del caso alcuni pazienti con la malattia avranno un valore
negativo del test. Tale tipo di errore casuale è non evitabile, ma
quantificabile attraverso l’intervallo di fiducia di sensibilità e specificità
del test.
Esempio. Test con Se=80%, Sp=70%.
Un nuovo test risulta positivo in 5 pazienti su 5 con la malattia (Se=100%) e negativo
in 9 pazienti su 10 senza malattia (Sp=90%).
Per la sensibilità: CI95%=(57% ÷ 100%)
Per la specificità: CI95%=(60% ÷ 98%)
Strategia: stimare la numerosità campionaria dello studio (soggetti da
includere con e senza la malattia) in modo da costruire un intervallo di
fiducia di una data dimensione per sensibilità e la specificità.
Suscettibilità degli studi sui test diagnostici
ad errori sistematici
• Di campionamento:
– campione non rappresentativo della popolazione alla
quale il test sarà applicato;
– prevalenza nel campione più alta della probabilità a
priori che si trova nella pratica clinica.
• Di misura:
– esito noto a chi misura la variabile predittiva (test);
– valutazione di risultati incerti.
• Di reporting:
– gli studi con risultati negativi non sono riportati.
Passi da seguire nella pianificazione di
uno studio per la valutazione di un test
diagnostico
•
•
•
•
C’è bisogno di un nuovo test diagnostico?
Come sono stati selezionati i soggetti?
C’è un gold standard ?
Il gold standard ed il nuovo test sono applicabili in modo
standardizzato ed in cieco?
• Determinazione della numerosità campionaria necessaria ad ottenere
un intervallo di fiducia di livello (1- )% per sensibilità e specificità
con una ragionevole precisione (p.e.: ±5%).
• Trovare un sufficiente numero di soggetti in modo da soddisfare la
numerosità calcolata.
• Riportare i risultati in termini di Se, Sp e potenziali VP+ e VP- a
differenti valori della probabilità a priori di malattia. Se il risultato del
test è categoriale o continuo riportare la curva ROC per descrivere la
performance del test.