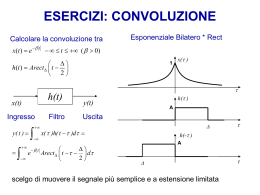
LUCIDI dell'insegnamento di
COMUNICAZIONI ELETTRICHE
eo/in/bi
PRIMA DI INTRAPRENDERE LO STUDIO DI QUESTO
MATERIALE E’ FONDAMENTALE LEGGERE ACCURATAMENTE
LA PAGINA:
http://www.arch.dibe.unige.it/ccl/dispense/Comunicazioni%20Elettriche/LucidiCE.htm
Attenzione: questi lucidi NON SONO PRIVI DI ERRORI
1.2
SEGNALI E SISTEMI
•
•
•
•
S.L.T.I
Integrale di Convoluzione
Autofunzioni
Trasformata di Fourier
SEGNALE
Sorgente
Tx
Canale
Segnale
Segnale
1.3
Dest.
Rx
Segnale
Segnale
SORGENTE : ES. MICROFONO, TELECAMERA, ETC. FORNISCE AL Tx L’ INFORMAZIONE PER
IL DESTINATARIO SOTTO FORMA DI GRANDEZZA (ES. ELETTRICA).
Tx : MANIPOLA UNA GRANDEZZA (ES. ELETTRICA); PERTURBA UNA GRANDEZZA
(ES. ELETTRICA, MECCANICA, E.M.,…).
CANALE : PROPAGA LA PERTURBAZIONE DELLA GRANDEZZA (ES. ELETTRICA,MECCANICA,..).
Rx : CONVERTE LA PERTURBAZIONE IN UNA GRANDEZZA (ES. ELETTRICA);
MANIPOLA TALE GRANDEZZA PER CONSENTIRE AL DESTINATARIO DI RICEVERE
L’ INFORMAZIONE EMESSA DALLA SORGENTE.
SEGNALE : E’ L’ ANDAMENTO DELLE GRANDEZZE CHE PORTANO L’ INFORMAZIONE DALLA
SORGENTE ALLA DESTINAZIONE.
1.4
SEGNALI
CONSIDERIAMO I SEGNALI IN ASTRATTO, INDIPENDENTEMENTE DAL TIPO
DI GRANDEZZA FISICA AD ESSI ASSOCIATA.
LI RAPPRESENTIAMO COMA FUNZIONI MATEMATICHE REALI () O
COMPLESSSE(C) DEFINITE TIPICAMENTE NEL DOMINIO DEL TEMPO (ES.x(t)).
POSSONO ANCHE ESSERE DEFINITI SU DOMINI DIVERSI A UNA O PIU’
DIMENSIONI (ES. DOMINIO SPAZIALE 2D).
ESEMPI : 1D  VOCE, DATI (x(t); x(nt))
2D  IMMAGINI (I(x,y))
1.5
RAPPRESENTAZIONE DEI SEGNALI
Continuo
TEMPO
Discreto
x nT 
x t 
t
t
Segnale analogico
Segnale campionato
x nT 
x t 
t
t
Segnale discreto
Segnale digitale
1.6
SEGNALI E SISTEMI
Tx
Canale
RX
Tx : SORGENTE DI INFORMAZIONE (TRASMETTITORE)
CANALE : MEZZO VETTORE PER L’INFORMAZIONE
Rx : UTENTE FINALE (RICEVITORE)
L’INFORMAZIONE DA TRASMETTERE É “CODIFICATA” NEL SEGNALE
REALE (VOCE, ......).
1-D (VOCE, DATI)
TIPI DI SEGNALI
2-D (SEGNALE TV)
1.7
SEGNALI
1) SEGNALI DETERMINISTICI : IL SEGNALE É NOTO ISTANTE
PER ISTANTE ( x(t) )
2) SEGNALI ALEATORI : NON É POSSIBILE CONOSCERE IL
VALORE DEL SEGNALE ISTANTE PER ISTANTE ( x(t) ESPRESSIONE
ANALITICA “TROPPO COMPLESSA” O NOTO SOLO SU BASE
STATISTICA ).
1.8
SISTEMI
x(t)
F(.)
y(t)
SISTEMA : QUALSIASI COSA CHE OPERA UNA “TRASFORMAZIONE”
SU DI UN SEGNALE x(t).
ESEMPIO : CANALE DI TRASMISSIONE
LINEA DI RITARDO (y(t)=x(t-T))
AMPLIFICATORE (y(t)=Ax(t))
1.9
ESEMPI DI SISTEMI
x t 
x t 
y t   Ax t 
A
Ritardo
Amplificatore ideale
y t   x t  T 
T
x t 
x t 
  2
y t   x 2  t 
Quadratore
y t   x t  cos t    Es. di modulatore
cos t   
1.10
SISTEMI LINEARI TEMPO INVARIANTI
(S.L.T.I.)
LINEARITA’ :
xi t   yi t 
x j t   y j t 
xi t   x j t   yi t   y j t 
(SOVRAPPOSIZIONE DEGLI EFFETTI)
TEMPO INVARIANZA :
xt   y t 
xi(t), xj(t); ,  
xt  T   y t  T 
x(t), t
1.11
S.L.T.I
PER QUESTI SISTEMI E’ INTERESSANTE STUDIARE IL SEGNALE
“RETTANGOLO”
R  t 
1
R  t 


t
: RETTANGOLO DI AREA UNITARIA
MOTIVO : CONOSCENDO LA RISPOSTA DI UN S.L.T.I. A
R  t 
PUO’ CALCOLARE LA RISPOSTA AD INGRESSI PIU’
COMPLESSI.
SI
1.12
x(t) : SEGNALE “GENERICO” (REALE)
x (t)

x(t)

N
x t    x n  R  t  n   
n0
IPOTESI :
“OPPORTUNAMENTE PICCOLO”
SI DEVE MOLTIPLICARE PER  POICHE’ R  t  HA
AMPIEZZA PARI A
VALORE DI
1 E SI DEVE CONSERVARE IL

x n 
1.13
R  t 
S.L.T.I
hR  t 
x t 
y t 
S.L.T.I
N
y t    x n   hR  t  n   
n0
DOVE hR : RISPOSTA A “RETTANGOLO UNITARIO”.
LIMITE DI:   0
y t  

 x   h t   d

h t   lim hR  t 
 0
1.14
INTEGRALE DI CONVOLUZIONE :
y t  

 x   h t   d

y t   x t  h t 
h t 
: RISPOSTA ALL’ IMPULSO DI AREA UNITARIA (“DELTA DI DIRAC”)
R  t 
1
0

 t
Lim 0

t
t
0
1.15
 t
E’ UNA “FUNZIONE GENERALIZZATA” ; E’ IMPORTANTE QUELLO CHE
FA PIU’ CHE IL VALORE CHE ASSUME.



f  x   x  dx = f  0
1.16
N.B : x t   t
 T   x t  T 
CONVOLUZIONE
LA CONVOLUZIONE TRA UN IMPULSO E UNA FUNZIONE GENERA LA
FUNZIONE STESSA TRASLATA NEL PUNTO DI APPLICAZIONE DELL’
IMPULSO.

f  t     t  T   f T     t  T 

f  t     t  T  dt  f  T 

PRODOTTO
IL PRODOTTO TRA UNA FUNZIONE ED UN IMPULSO HA L’ EFFETTO DI
CAMPIONARE LA FUNZIONE IN UN ISTANTE.
1.17
RISPOSTA ALL’ IMPULSO
 h t  
INTEGRALE DI CONVOLUZIONE
y t  
 x h

 x    h t   d 
CAMBIO DI VARIABILE
t  



 h x t    d  x t  h t   h t  x t 

SISTEMI CAUSALI : h t 
E’ DIVERSA DA 0 SOLO PER t >O
1.18
INTERPRETAZIONE GRAFICA DI: y(t)=x(t)*h(t)
h(t- )
h( )
x( )
t
,t
t
t=0
h    )
•“FACCIO SCORRERE h t   
t
•“RIBALTO” (ottengo
•“MOLTIPLICO E INTEGRO”

 x   h t   d


ESEMPIO DI CALCOLO DELL’ INTEGRALE
DI
CONVOLUZIONE PER VIA GRAFICA
DATI :
h(t)
1
RISPOSTA
0
2T
T
t
3T
ALL’IMPULSO
DI UN SISTEMA
-2
x(t)
3
2
INGRESSO
1
2T
-2T
-T
0
T
- -1
DETERMINARE L’USCITA y(t) del SISTEMA.
t
1.19
1.20
SAPPIAMO CHE :
y t   x t  h t  

 x  h t    d

LAVORIAMO PER VIA GRAFICA. OCCORRE RIBALTARE h(t) :
h(- )
Cambiato nome della variabile di
integrazione
1
-3T
-2T
-T

0
-1
-2
LASCIAMO INALTERATA x(t), SI PUO’ EFFETTUARE IL PRODOTTO TRA x(t)
E h(-) ED INTEGRARE :
y 0  T 1  2  2  1  0
1.21
A QUESTO PUNTO SI PUO’ TRASLARE LA h(t) DI ALTRE QUANTITA’ QUINDI CON LO
STESSO METODO RICAVARE LE y RELATIVE.
TABULANDO LA y AD INTERVALLI T SI OTTIENE:
y(t)
t
y(t)
-2T
0
4T
-T
-T
T
5T
0
0
T
T
0
2T
-5T
3T
5T
t
1.22
SI NOTI CHE PER VALORI DI t COMPRESI TRA MULTIPLI DI T , LA y VARIA LINEARMENTE
CON IL PARAMETRO, E QUINDI LA TABELLA E’ SUFFICIENTE A DESCRIVERE
COMPLETAMENTE L’USCITA.
y(t)
5T
-T
2T
-2T
-T
0
-T
-5T
T
3T
4T
5T
t
1.23
ALLO STESSO RISULTATO SI ARRIVA RIBALTANDO E TRASLANDO x(t)
E MANTENENDO INALTERATA h(t).
PROPRIETA’ DELL’ INTEGRALE DI CONVOLUZIONE:
DURATA DEL RISULTATO DI CONVOLUZIONE E’ LA SOMMA DELLA
DURATA DEGLI OPERANDI DELLA CONVOLUZIONE.
1.24
ESEMPI DI h(t)
• FILTRI
h(t)
(ideali)
(non realizzabili)
h(t)
+1
t
+1
t
-1
“PASSA BASSO”
“PASSA ALTO”
(“Integratore”)
(“Derivatore”)
• CIRCUITO RC:
h(t)
A
Ae
 t RC
“E’ UNA SPECIE DI INTEGRATORE”
x(t)
t
RC
R
y(t)
C
t
 u t 
t
1.25
IN BASE AL VALORE DI RC POSSO AVERE:
Vu(t)
T 
Vi(t)
Vi(t)
t
Vu(t)
t

T 
Vi(t)
 RC
t
1.26
ESEMPIO DI CALCOLO ANALITICO
DELL’INTEGRALE DI CONVOLUZIONE
R
u(t)gradino
SI VUOLE CALCOLARE L’USCITA y(t).
C
y(t)
h t   Ae t  u t 
y t  

A    1 RC
 u  h t    d
h t     Ae   t    u t   

MA:
• u()=0 SE <0
• h() E’ UN SISTEMA CAUSALE h(t- )=0 SE t- <0   >t
1.27
QUINDI : (t>0)
y t  
t


0
 Ae
t
t


  t  
t

Ae
d  Ae   e d  
0

e


t
0


1  e t   u t 

A
y(t)
A/ 
=1
Uscita nulla per t  0
t
y(t) TENDE AD ESSERE UNA RAMPA  EFFETTO INTEGRATIVO
( FILTRO PASSA BASSO)
1.28
OSSERVAZIONI
SULL’ INTEGRALE DI CONVOLUZIONE
• L’ effetto di h(t) sul segnale x(t) dipende dalla “forma” di h(t).
• Allungamento durata temporale
(y(t) dura piu’ di x(t) e h(t))
• Per calcolare l’ integrale di convoluzione per via “ grafica
conviene “ribaltare” la funzione piu’ semplice fra x(t) e y(t).
1.29
ES. CALCOLO INTEGRALE DI
CONVOLUZIONE
PER VIA GRAFICA
 1>  2
1
2
“RIBALTO x2(t)”
“FACCIO SCORRERE x2(t)”
v1
x1
v2
x2
x2  t   
x 2   
x1
t
t
a
b
c
d
-d
-c
a
b
1   2
y(t)
v1  v2   1
ESTENSIONE DURATA
1   2
a+c
b+d
1   2
t
1.30
IMPULSO DI DIRAC
(t)
Durata nulla
Altezza 
Area unitaria
DEF :

+

-
Funzione generalizzata
   t dt  1    t  x t  dt  x 0
“HA SENSO SOLO SOTTO INTEGRALE” ANCHE SE NOI LA USEREMO
SPESSO SENZA INTEGRALE.
RITARDO
x t   1 t   t  T   x t  T   1 t  T  1 t   u t 
CAMPIONAMENTO
x t     t  T   x T     t  T 

 x      T  d

 x T 