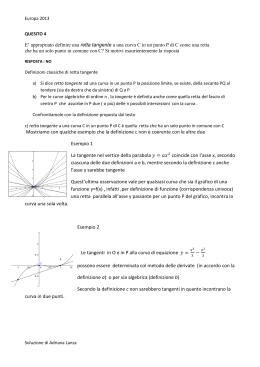
Retta tangente
Materiale integrativo del
Corso integrato di
Matematica
per le scienze naturali ed applicate
Paolo Baiti, Lorenzo Freddi
Retta tangente - Capitolo 19: Applicazioni del calcolo differenziale - pagina 172
- p. 1/4
Retta tangente
Sia f :]a, b[→ R continua e x0 ∈]a, b[
Retta tangente
Significato geometrico
Esempio
f (x0 )
P0
x0
Retta tangente - Capitolo 19: Applicazioni del calcolo differenziale - pagina 172
- p. 2/4
Retta tangente
Sia f :]a, b[→ R continua e x0 ∈]a, b[
Retta tangente
Significato geometrico
Esempio
Tracciamo la retta secante passante per i punti di
ascissa x0 e x0 + h.
f (x0 + h)
f (x0 )
Ph
P0
x0
Equazione della secante:
y = (x − x0 )
Retta tangente - Capitolo 19: Applicazioni del calcolo differenziale - pagina 172
x0 + h
f (x0 + h) − f (x0 )
+ f (x0 )
h
- p. 2/4
Retta tangente
Sia f :]a, b[→ R continua e x0 ∈]a, b[
Retta tangente
Significato geometrico
Esempio
Tracciamo la retta secante passante per i punti di
ascissa x0 e x0 + h.
f (x0 + h)
Ph
Facciamo tendere h a zero,
quindi x0 + h tenderà a x0 .
f (x0 )
P0
x0
Equazione della secante:
y = (x − x0 )
Retta tangente - Capitolo 19: Applicazioni del calcolo differenziale - pagina 172
x0 + h
f (x0 + h) − f (x0 )
+ f (x0 )
h
- p. 2/4
Retta tangente
Sia f :]a, b[→ R continua e x0 ∈]a, b[
Retta tangente
Significato geometrico
Esempio
Tracciamo la retta secante passante per i punti di
ascissa x0 e x0 + h.
Facciamo tendere h a zero,
quindi x0 + h tenderà a x0 .
f (x0 + h)
f (x0 )
Corrispondentemente
il
punto Ph tenderà a P0
lungo la curva.
Equazione della secante:
Ph
P0
x0
y = (x − x0 )
Retta tangente - Capitolo 19: Applicazioni del calcolo differenziale - pagina 172
x0 + h
f (x0 + h) − f (x0 )
+ f (x0 )
h
- p. 2/4
Retta tangente
Sia f :]a, b[→ R continua e x0 ∈]a, b[
Retta tangente
Significato geometrico
Esempio
Tracciamo la retta secante passante per i punti di
ascissa x0 e x0 + h.
Facciamo tendere h a zero,
quindi x0 + h tenderà a x0 .
f (x0 + h)
f (x0 )
Corrispondentemente
il
punto Ph tenderà a P0
lungo la curva.
Equazione della secante:
Ph
P0
x0
y = (x − x0 )
Retta tangente - Capitolo 19: Applicazioni del calcolo differenziale - pagina 172
x0 + h
f (x0 + h) − f (x0 )
+ f (x0 )
h
- p. 2/4
Retta tangente
Sia f :]a, b[→ R continua e x0 ∈]a, b[
Retta tangente
Significato geometrico
Esempio
Tracciamo la retta secante passante per i punti di
ascissa x0 e x0 + h.
Facciamo tendere h a zero,
quindi x0 + h tenderà a x0 .
f (x0 + h)
f (x0 )
Corrispondentemente
il
punto Ph tenderà a P0
lungo la curva.
Equazione della secante:
Ph
P0
x0 x0 + h
y = (x − x0 )
Retta tangente - Capitolo 19: Applicazioni del calcolo differenziale - pagina 172
f (x0 + h) − f (x0 )
+ f (x0 )
h
- p. 2/4
Retta tangente
Sia f :]a, b[→ R continua e x0 ∈]a, b[
Retta tangente
Significato geometrico
Esempio
Per h → 0, la retta secante
tende alla
retta tangente al grafico
nel punto x0 , f (x0 )
f (x0 )
P0
x0
Equazione della secante:
y = (x − x0 )
Retta tangente - Capitolo 19: Applicazioni del calcolo differenziale - pagina 172
f (x0 + h) − f (x0 )
+ f (x0 )
h
- p. 2/4
Retta tangente
Sia f :]a, b[→ R continua e x0 ∈]a, b[
Retta tangente
Significato geometrico
Esempio
Per h → 0, la retta secante
tende alla
retta tangente al grafico
nel punto x0 , f (x0 )
Se f è derivabile in x0 , passando al limite h → 0 nell’equazione della retta secante si trova l’equazione
della retta tangente
Equazione della secante:
f (x0 )
P0
x0
y = (x − x0 )
Retta tangente - Capitolo 19: Applicazioni del calcolo differenziale - pagina 172
f (x0 + h) − f (x0 )
+ f (x0 )
h
- p. 2/4
Retta tangente
Sia f :]a, b[→ R continua e x0 ∈]a, b[
Retta tangente
Significato geometrico
Esempio
Per h → 0, la retta secante
tende alla
retta tangente al grafico
nel punto x0 , f (x0 )
Se f è derivabile in x0 , passando al limite h → 0 nell’equazione della retta secante si trova l’equazione
della retta tangente
Equazione della secante:
f (x0 )
P0
x0
y = (x − x0 )
f (x0 + h) − f (x0 )
+ f (x0 )
h
y = (x − x0 )f ′ (x0 ) + f (x0 )
Retta tangente - Capitolo 19: Applicazioni del calcolo differenziale - pagina 172
- p. 2/4
Retta tangente
Sia f :]a, b[→ R continua e x0 ∈]a, b[
Retta tangente
Significato geometrico
Esempio
Per h → 0, la retta secante
tende alla
retta tangente al grafico
nel punto x0 , f (x0 )
Se f è derivabile in x0 , passando al limite h → 0 nell’equazione della retta secante si trova l’equazione
della retta tangente
Equazione della secante:
f (x0 )
P0
x0
y = (x − x0 )
Equazione della tangente in P0 :
Retta tangente - Capitolo 19: Applicazioni del calcolo differenziale - pagina 172
f (x0 + h) − f (x0 )
+ f (x0 )
h
y = (x − x0 )f ′ (x0 ) + f (x0 )
- p. 2/4
Significato geometrico della derivata
Dall’equazione
Retta tangente
Significato geometrico
Esempio
y = (x − x0 )f ′ (x0 ) + f (x0 )
si ottiene l’interpretazione geometrica della derivata:
La derivata della funzione f nel punto
x0 è il coefficiente angolare della retta tangente al grafico della funzione nel
punto (x0 , f (x0 ))
Retta tangente - Capitolo 19: Applicazioni del calcolo differenziale - pagina 172
- p. 3/4
Esempio
Sia f (x) = x2 .
Retta tangente
Significato geometrico
Esempio
1
1
Retta tangente - Capitolo 19: Applicazioni del calcolo differenziale - pagina 172
- p. 4/4
Esempio
Sia f (x) = x2 .
Consideriamo la retta secante passante per i punti del grafico di
ascissa 1 e x.
Retta tangente
Significato geometrico
Esempio
x2
1
1
Retta tangente - Capitolo 19: Applicazioni del calcolo differenziale - pagina 172
x
- p. 4/4
Esempio
Sia f (x) = x2 .
Consideriamo la retta secante passante per i punti del grafico di
ascissa 1 e x.
Il coefficiente angolare è
Retta tangente
Significato geometrico
Esempio
x2
x2 − 1
m(x) =
x−1
1
1
Retta tangente - Capitolo 19: Applicazioni del calcolo differenziale - pagina 172
x
- p. 4/4
Esempio
Sia f (x) = x2 .
Consideriamo la retta secante passante per i punti del grafico di
ascissa 1 e x.
Il coefficiente angolare è
2
x −1
m(x) =
x−1
Retta tangente
Significato geometrico
Esempio
x2
Facciamo variare x 6= 1
1
1
Retta tangente - Capitolo 19: Applicazioni del calcolo differenziale - pagina 172
x
- p. 4/4
Esempio
Sia f (x) = x2 .
Consideriamo la retta secante passante per i punti del grafico di
ascissa 1 e x.
Il coefficiente angolare è
x2 − 1
m(x) =
x−1
Retta tangente
Significato geometrico
Esempio
x2
Facciamo variare x 6= 1
1
1
Retta tangente - Capitolo 19: Applicazioni del calcolo differenziale - pagina 172
x
- p. 4/4
Esempio
Sia f (x) = x2 .
Consideriamo la retta secante passante per i punti del grafico di
ascissa 1 e x.
Il coefficiente angolare è
x2 − 1
m(x) =
x−1
Retta tangente
Significato geometrico
Esempio
x2
Facciamo variare x 6= 1
1
1
Retta tangente - Capitolo 19: Applicazioni del calcolo differenziale - pagina 172
x
- p. 4/4
Esempio
Sia f (x) = x2 .
Consideriamo la retta secante passante per i punti del grafico di
ascissa 1 e x.
Il coefficiente angolare è
Retta tangente
Significato geometrico
Esempio
x2 − 1
m(x) =
x−1
Facciamo variare x 6= 1
x2
1
1 x
Retta tangente - Capitolo 19: Applicazioni del calcolo differenziale - pagina 172
- p. 4/4
Esempio
Sia f (x) = x2 .
Consideriamo la retta secante passante per i punti del grafico di
ascissa 1 e x.
Il coefficiente angolare è
Retta tangente
Significato geometrico
Esempio
x2 − 1
m(x) =
x−1
Facciamo variare x 6= 1
x2
1
1x
Retta tangente - Capitolo 19: Applicazioni del calcolo differenziale - pagina 172
- p. 4/4
Esempio
Sia f (x) = x2 .
Consideriamo la retta secante passante per i punti del grafico di
ascissa 1 e x.
Il coefficiente angolare è
Retta tangente
Significato geometrico
Esempio
x2 − 1
m(x) =
=x+1
x−1
Facciamo variare x 6= 1
x2
1
1x
Retta tangente - Capitolo 19: Applicazioni del calcolo differenziale - pagina 172
- p. 4/4
Esempio
Sia f (x) = x2 .
Consideriamo la retta secante passante per i punti del grafico di
ascissa 1 e x.
Il coefficiente angolare è
Retta tangente
Significato geometrico
Esempio
x2 − 1
m(x) =
=x+1
x−1
Facciamo variare x 6= 1
Al “limite”, quando x tende a 1,
m(x) tende al coefficiente angolare della retta tangente in x = 1;
scriveremo
1
1
f ′ (1) = lim m(x) = 2
x→1
Retta tangente - Capitolo 19: Applicazioni del calcolo differenziale - pagina 172
- p. 4/4