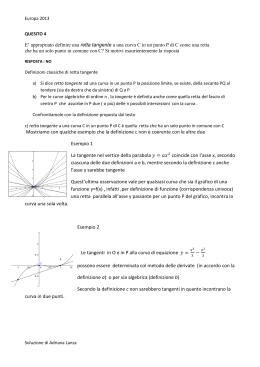
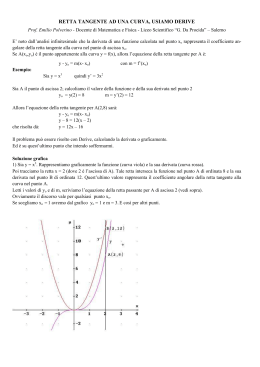
Problema retta tangente:
Come definiamo la retta tangente in un punto
ad una curva?
Nel caso di alcune
curve, come la
circonferenza,
diremmo:
“La retta tangente è
quella retta che ha un
solo punto, o meglio,
due coincidenti, in
comune con la curva”
Questa definizione però non è sempre
accettabile:
Una retta può
essere tangente in
un punto della
curva e secante in
un altro!
P
La retta è tangente in P e secante in Q.
Q
Come fare allora?
Consideriamo due punti
A e B e la retta secante
alla curva in A e B.
Quindi immaginiamo
di tenere fisso A e di
avvicinare B ad A,
ritracciando di volta in
volta le rette secanti.
B B
B
B=A
A
Quando B coinciderà con A che retta avrò
ottenuto?
La retta ottenuta è la tangente alla curva nel punto A
Nuova definizione di retta tangente
“La retta tangente
ad una curva in un
suo punto A è la
posizione limite
della secante AB al
tendere del punto B
al punto A”
B B
NB:perché la chiamo posizione limite?
B A
Ci serviamo delle nostre conoscenze di analisi per
determinare l’equazione della tangente ad una curva
Sia y=f(x) una funzione.
Prendiamo un punto A sulla
curva :
A( c ; f(c) )
poi un punto B
B ( c+h ; f(c+h) )
Chi è il coefficiente angolare
della retta secante AB?
m AB
y B  y A f (c  h )  f (c )


xB  x A
h
B
A
Tale rapporto si indica con
y f (c  h)  f (c)

x
h
e prende il nome di
RAPPORTO
INCREMENTALE
della funzione relativo
ac.
Significato geometrico: il
rapporto incrementale è il
coefficiente angolare della
retta secante passante per
A(c,f(c)) e B(c+h,f(c+h)).
B
A
Alla luce della nuova definizione, chi sarà la retta tangente
alla curva nel punto A?
Graficamente otteniamo la retta tangente avvicinando B ad
A, ovvero riducendo la distanza h tra l’ascissa di A e
l’ascissa di B
B
A
A
B
A
B
A
Qual è l’equazione di tale retta tangente?
Per conoscere la retta tangente dovremmo conoscere un
punto per cui passa e il suo coefficiente angolare.
y  y A  mt ( x  x A )
La retta tangente passa per A(c ; f(c) )
Ma chi è il suo coefficiente angolare ?
Se la retta tangente si ottiene come posizione limite della
secante al tendete di B ad A, cioè riducendo la distanza h,
lo stesso vale per il coefficiente angolare:
Il coefficiente angolare della tangente si ottiene
calcolando il limite del coefficiente angolare della
secante per h che tende a zero.
f (c  h )  f (c )
mt  lim
h 0
h
Una funzione si dice derivabile in punto c del suo dominio
se esiste il limite finito del rapporto incrementale della
funzione nel puto c per h che tende a zero.
Tale limite prende il nome di DERIVATA PRIMA della
funzione nel punto c e si scrive
f (c  h)  f (c )
f ' (c)  lim
h 0
h
Significato geometrico: la derivata prima della funzione
nel punto c è il coefficiente angolare della retta
tangente alla curva nel punto (c; f(c)).