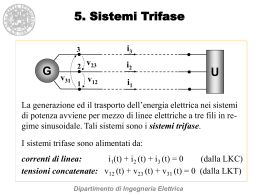
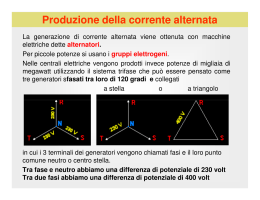
Rete di alimentazione monofase
Esempio elementare di sistema di alimentazione monofase:
un generatore bipolare (per semplicità ideale) alimenta,
tramite una connessione, un carico bipolare (un’impedenza)
Elettrotecnica
Eg
+
17 Reti trifasi
.
Z
I
1
Rete trifase elementare
Rete trifase elementare
Con tre sistemi di alimentazione monofase elementari si
come il precedente (3 generatori ideali, 3 connessioni e 3
impedenze……
E g1
E g2
E g3
+ 1g
I1
+ 2g
I2
+ 3g
I3
1u
2u
3u
2
…. si realizza un sistema di alimentazione trifase
(elementare): le tre connessioni di ritorno sono fuse in una
soltanto, senza alterare tensioni e correnti
Z˙ 1
Z˙ 2
Z˙ 3
3
E g1
+
1g
I1
1u
Z˙ 1
E g2
+
2g
I2
2u
Z˙ 2
E g3
+
3g
I3
3u
Z˙ 3
0g
I0
0u
4
Rete trifase elementare con neutro
Rete trifase elementare senza neutro
Si è ottenuto un sistema trifase a 4 fili: il conduttore di
ritorno comune è detto neutro ed interconnette i 2 centri
stella 0g e 0u (necessariamente accessibili); i conduttori
1, 2 e 3 sono detti fasi. Per la LKC è:
Rimuovendo il conduttore di neutro, si ottiene un sistema
trifase a 3 fili (le 3 fasi), i centri stella non sono connessi
(in genere sono inaccessibili) e per la LKC:
I0 = I1 + I2 + I3
I1 + I2 + I3 = 0
E g1
E g2
!
E g3
I1
1g
+
+
+
2g
I2
3g
I3
Z˙ 1
2u
Z˙ 2
+
1g
I1
1u
Z˙ 1
E g2
+
2g
I2
2u
Z˙ 2
E g3
+
3g
I3
3u
Z˙ 3
E g1
!
Z˙ 3
3u
I0
0g
1u
0u
5
6
Generatori trifasi
Carichi trifasi
Presentano 3 percorsi interni, o fasi interne, in ciascuna delle quali è
prodotta una tensioni impressa che, per semplicità, può essere
rappresentata come generatore ideale di tensione.
Le topologie possono essere:
a stella con neutro (
o Yn), a stella senza neutro (
o Y),
a triangolo (! o D).
–
E g1
–
E g2
–
E g3
+
+
+
1
2
3
–
E g1
–
E g2
–
E g3
Nei casi più semplici, anche i carichi (o utenze) presentano 3 percorsi
interni, o fasi interne, ciascuno dei quali è rappresentabile come un
impedenza:
Se le 3 impedenze sono uguali si dice che il carico è equilibrato.
Le topologie possono essere:
a stella con neutro, a stella senza neutro, a triangolo
+
+
1
+
1
–
E g1
–
E g3
2
–+
E g2
+
3
1
Z
1
Z
2
2
3
3
Z
1
.
.
.
.
Z
Z
2
.
Z
Z
3
.
Z
2
.
Z
3
0
0
a ) stella con neutro
.
.
+
b) stella senza neutro
c) triangolo
a ) stella con neutro
7
b) stella senza neutro
c) triangolo
8
Terne di tensione 1
In un sistema a 4 fili, il centro
stella 0 è accessibile e tra ogni
fase ed esse è presente una
tensioni di fase. Queste
costituiscono la terna delle
tensioni di fase, o anche terna
delle tensioni stellate, perchè i
loro fasori vengono rappresentati
tipicamente a stella.
generatore
Terne di tensione 2
1g
1u
2g
2u
3g
3u
0g
0u
Invece tra ogni coppia di fasi è
presente una tensione
concatenata. Queste
costituiscono la terna delle
tensioni concatenate, o anche
terna delle tensioni a triangolo,
perchè i loro fasori vengono
rappresentati tipicamente a
triangolo.
utente
rete trifase a quattro fili o rete trifase con neutro
E1
0
E2
E2
2
3
E3
3
2
terna diretta di tensioni stellate
2g
2u
3g
3u
0g
0u
utente
1
E1
0
1u
rete trifase a quattro fili o rete trifase con neutro
1
1
Se le tre tensioni hanno uguale
ampiezza (e ugual valore
efficace) e sfasamenti di 2"/3
(=120°) si dice che la terna è
E3
simmetrica
generatore
1g
Se le tre tensioni hanno uguale
ampiezza (e ugual valore
efficace) e sfasamenti di 2"/3
(=120°) si dice che la terna è
simmetrica
terna inversa di tensioni stellate
U31
3
1
U12
U12
2
U23
U31
2
terna diretta di tensioni concatenate
3
U23
terna inversa di tensioni concatenate
9
Terne di tensione 3
Se le due terne sono
simmetriche tra i
valori efficaci sussiste
la relazione:
Es.:
3E
E=127 V e U=220 V
E=220 V e U=380 V
In un sistema a 3 fili, ove i
centri stella non sono accessibili,
sono presenti solo le tre tensioni
concatenate tra fase e fase,
ovvero la terna delle tensioni
concatenate, o a triangolo, i
fasori essendo disposti
tipicamente a triangolo.
.
1
1
U 31
!
E3
U=
Terne di tensione 4
# U12 = E1 " E2
%
$U23 = E2 " E3
%U = E " E
& 31
3
1
Per la LKT tra tensioni stellate e
tensioni concatenate valgono le
relazioni:
3
E1
0
E2
U23
terne simmetriche dirette
E1
U12
U12
2
2
E2
0
U31
E3
1g
1u
2g
2u
generatore
3g
3
utente
3u
sistema trifase a tre fili o
sistema trifase senza neutro
1
Terne simmetriche
U31
1
U12
U12
U23
U31
terne simmetriche inverse
3
U23
2
terna diretta di tensioni concatenate
11
!
10
2
U23
3
terna inversa di tensioni concatenate
12
Terne di corrente 1
Nei 3 conduttori di fase sono
presenti 3 correnti, che
costituiscono la terna delle
correnti di linea.
1g
I1
1u
2g
I2
2u
generatore
3g
I3
3u
0g
I0
0u
utente
1g
I1
1u
2g
I2
2u
3g
I3
generatore
Se le tre correnti hanno uguale a) sistema trifase a quattro fili
ampiezza (e ugual valore
efficace) e sfasamenti di 2"/3
(=120°) si dice che la terna è
I2
simmetrica
In tal caso vale comunque (anche I1
se è presente il neutro):
I1 + I2 + I3 = 0
Terne di corrente 2
Sistemi a 4 fili
Se la terna delle correnti di linea è simmetrica e quindi con somma
nulla, il neutro ha corrente nulla
utente
3u
I0 = I1 + I2 + I3 = 0
per il teorema di sostituzione può essere rimosso senza che tensioni e
correnti siano modificate.
b) sistema trifase a tre fili
!
I2
I1
I3
I3
terne simmetriche dirette
terne simmetriche inverse
Quindi: se le correnti (e tensioni) sono certamente simmetriche, sono
sufficienti i soli 3 conduttori di fase, con risparmio di materiale
conduttore. Avviene nei sistemi in:
AAT = altissima tensione -Y-,
AT = alta tensione - YMT = media tensione -D-
13
14
!
Terne di corrente 3
Sistemi a 3 fili con collegamento a
triangolo delle fasi interne
Oltre alla terna delle correnti di linea è
presente la terna delle correnti di fase
interna.
Per la LKC valgono le relazioni:
Terne di corrente 4
Sistemi a 3 fili con collegamento a
triangolo delle fasi interne
I1
1
#I = J " J
12
31
% 1
$ I2 = J 23 " J12
%I = J " J
& 3
31
23
I2 J 1 2
2
J3 1
I3 J 2 3
Se entrambe le terne di corrente
sono simmetriche tra i
3
#I = J " J
12
31
% 1
$ I2 = J 23 " J12
%I = J " J
& 3
31
23
valori efficaci sussiste
la relazione:
I = 3J
!
J1 2
I2
J2 3
I1
J3 1
I3
terne simmetriche dirette
!
I2
J1 2
J2 3
I3
I1
J3 1
terne simmetriche inverse
!
15
16
Sistemi simmetrici ed equilibrati
Se le terne di tensione impresse
sono simmetriche ed i carichi sono
equilibrati, allora anche le terne di
corrente sono simmetriche.
Ad esempio per sistemi con
collegamenti a stella a 4 o 3 fili (con
o senza neutro), per ogni fase si ha:
I1 =
1g
–
+ E g2
2g
–
+ E g3
3g
0g
E
E1
E
, I 2 = 2 , I3 = 3
&Z
&Z
Z&
I 0 = I1 + I 2 + I 3 = 0
–
+ E g1
I1
I2
I3
I0
1u
.
Z
2u
.
Z
3u
.
Z
Sistemi squilibrati 1
Se le terne di tensione impresse
sono simmetriche ma i carichi sono
squilibrati, allora le terne di
corrente sono dissimmetriche.
Nei sistemi a 4 fili il neutro ha
corrente in generale non nulla:
0u
E1
–
+ E g2
2g
–
+ E g3
3g
I1
I2
I3
I0
0g
E1
!
!
E2
E3
!
E2
I2
terne dirette
.
Z
2u
.
Z
3u
.
Z
0u
I3
I1
!1
I 0 = I1 + I 2 + I 3 ! 0
I2
!
1u
E1
I1
!
I3
E la sua rimozione altera i valori
delle tensioni e correnti. In
particolare senza neutro i carichi a
stella non hanno tensioni uguali a
quelle impresse dai generatori
I0
!3
I3
I2
E3
!2
E2
terne inverse
17
Sistemi squilibrati 2
Dunque in un sistema con terne
di tensione impresse simmetriche
e carichi squilibrati, ove le terne
di corrente sono dissimmetriche,
il filo di neutro è indispensabile
per garantire che ai carichi
collegati a stella siano applicate
le tensioni stellate nominali del
sistema. Avviene nei sistemi in:
1g
E
E
E
I1 = 1 , I 2 = 2 , I 3 = 3
&Z
&Z
Z&
I1
!
E3
–
+ E g1
–
+ E g1
1g
–
+ E g2
2g
–
+ E g3
3g
0g
I1
I2
I3
I0
18
Potenza trifase 1
1u
.
Z
2u
.
Z
3u
.
Z
In un sistema trifase simmetrico
ed equilibrato (con o senza neutro,
per quanto visto) la potenza
elettrica trifase istantanea,
pari alla somma delle potenze
istantanee delle tre fasi, è:
0u
BT = bassa tensione -Yn-,
1
W1
2
W2
W3
3
0
pt(t) = e1(t)i1(t) + e2(t)i2(t) + e3(t)i3(t)
Ove ogni carico è costituito da un singolo utente (o gruppo di utenti)
monofase (ad esempio utenti residenziali).
Ove ciascuna delle tre potenze è costituita dalla somma della potenza attiva,
costante, e della potenza fluttuante, a pulsazione 2#:
e1(t)i1(t) = P1 + pf1(t) = EI cos! - EI cos (2#t+2$1+%) ........
19
20
Potenza trifase 2
Potenza trifase 3
Essendo le terne di tensione e corrente simmetriche, le tre potenze
fluttuanti risultano uguali in ampiezza e sfasate mutuamente di 2"/3, cosicché
hanno somma identicamente nulla:
In un sistema trifase senza
neutro (simmetrico o non
simmetrico, equilibrato o
squilibrato), vale la relazione,
già vista:
pf1(t) + pf2(t) + pf3(t) = 0
mentre le tre potenze attive risultano uguali. Pertanto la potenza istantanea
trifase risulta costante e uguale alla potenza attiva trifase, pari al triplo
della potenza attiva di una fase:
i1 +i2 +i3 =0
––
pt(t) = Pt = 3EI cos! = "3UI cos!
=>
1g i 1 (t)
1u
2g i 2 (t)
2u
generatore
3g i 3 (t)
utente
3u
i2 =–i1 –i3
Che permette di pensare il sistema trifase senza neutro anche come
un sistema bifase, in cui il conduttore di fase 2 è la connessione
comune dei conduttori di fase 1 e 3, e le tensioni di fase sono le due
concatenate u12 e u32.
La potenza reattiva trifase e la potenza apparente trifase sono:
––
Qt = 3EI sen! = "3UI sen!
––
At = 3EI = "3UI
21
22
Potenza trifase 3
Potenza trifase 4
Pertanto la potenza del sistema trifase senza neutro, pari alla potenza di tale
sistema bifase, è:
Pertanto la misura della potenza trifase in un sistema a 3 fili o a 4 fili con
corrente nulla nel neutro può essere eseguita usando due soli wattmetri in
inserzione Aron:
ptsn =u12i1 +u32i3
W1 2
Che coincide con quella trifase del sistema a 4 fili:
1
2
pt(t) = e1(t)i1(t) + e2(t)i2(t) + e3(t)i3(t)
fintantoché la corrente del neutro è nulla.
W3 2
3
Ove ciascuno dei due wattmetri indica la potenza di uno dei due addendi della
ptsn =u12i2 +u32i3
23
24