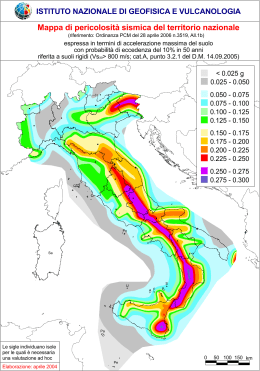
Corso di Aggiornamanto:
STUDI DI MICROZONAZIONE SISMICA:
TEORIA E APPLICAZIINI
SISMICITA’ E
PERICOLOSITA’ SISMICA
Aosta 18-19 Ottobre 2011
Vivaio Regionale di Olleyes
Sommario
 Pericolosità sismica
 Pericolosità sismica della Liguria.
Pericolosità sismica
La Pericolosità sismica può essere definita come il livello di confidenza associato
ad una proposizione del tipo: “ in un futuro intervallo di tempo Δt la località S
verrà interessata da almeno un evento sismico caratterizzato da un livello di
scuotimento al sito >= Is “ .
Questo livello di confidenza è generalmente codificato in termini di valori di
probabilità: più in generale, esisterà una curva di probabilità cui elementi
rappresentano i valori di probabilità associati ai diversi gradi di scuotimento atteso
nell’intervallo di esposizione Δt.
Il livello di confidenza dipende dalla qualità e affidabilità delle conoscenze a
nostra disposizione per la valutazione dello scuotimento atteso. Quindi, la
pericolosità deve risultare dalla combinazione delle informazioni effettivamente
disponibili corredate da una caratterizzazione credibile del livello di incertezza ad
esse associato.
Pericolosità sismica
In generale, la stima della pericolosità sismica richiede:
 caratterizzazione delle sorgenti sismogeniche (sismicità storica)
potenzialmente pericolose sia in termini di localizzazione spaziale
che di dinamica temporale;
 definizione delle modalità di trasmissione dell’energia dalla
sorgente al sito di interesse (i.e legge di attenuazione);
 individuazione di possibili effetti locali capaci di modificare il
livello di scuotimento atteso.
Pericolosità sismica
• Ingredienti: catalogo dei terremoti; caratterizzazione delle sorgenti sismiche ; leggi di
attenuazione; metodi statistici per la valutazione dell’hazard.
• Preparazione (metodologia di Cornell, 1968):
1- caratterizzazione delle sorgenti; deve essere quantificata la distribuzione della probabilità di
rottura per ogni punto della sorgente sismica. Nella maggior parte dei casi si considera una
distribuzione uniforme della probabilità per ogni zona sorgente; questo implica che i terremoti hanno
la stessa possibilità di verificarsi indipendentemente dalla posizione della rottura. Queste
distribuzioni vengono poi correlate con la geometria della sorgente per ottenere la corrispondente
distribuzione della probabilità di rottura in funzione della distanza sorgente-sito;
2- quantificazione del grado di attività di ciascuna sorgente mediante parametri magnitudofrequenza. Per mezzo di una relazione statistica (es. legge di Gutenberg-Richter), che esprime la
distribuzione dei terremoti di magnitudo superiore ad un valore m nel tempo (Log (N° terremoti > m,
dove m sta per magnitudo)), si definisce la sismicità della sorgente in esame;
3- stima dello scuotimento provocato
al sito d’interesse da un terremoto di
qualsiasi magnitudo in funzione della
distanza sorgente-sito mediante
l’impiego di leggi di attenuazione;
Y
Pericolosità sismica
4- calcolo della probabilità che lo
scuotimento, definito da opportuni
parametri (picco di accelerazione
orizzontale (PGA), picco di velocità
(PGV), di spostamento, ecc.), sia
superato in un dato intervallo
temporale (P[Y > y*]).
L’approccio probabilistico (PSHA: Probabilistic Seismic Hazard
Analysis), permette quindi di stimare la probabilità che si verifichi un
determinato scuotimento in funzione del tempo
Pericolosità sismica: zonazione
• Una zonazione sismogenetica consiste in unità sismotettoniche ognuna delle quali rappresenta il
contour della proiezione in superficie di tutte le strutture considerate sorgenti di terremoti ad alta
e bassa energia.
• Ogni zona sismogenetica viene assunta quale
omogenea, cioè si suppone che i terremoti
possano verificarsi in ogni suo punto con la
stessa probabilità. Se da un lato questa
assunzione
rappresenta
una
netta
semplificazione, dall’altro consente di valutare
in tempi ragionevoli la pericolosità sismica di
qualsiasi area.
• La tracciatura di una zonazione sismogenetica
consegue da osservazioni a carattere geologicostrutturale,
geodinamico,
cinematico
e
sismologico
Zonazione sismogenetica ZS4 (Meletti et al., 2000)
Pericolosità sismica: leggi di ricorrenza
• La distribuzione temporale dei terremoti in funzione della loro magnitudo (distribuzione magnitudofrequenza) è descritta da relazioni statistiche (recurrence laws). Tra questa la più nota è quella di
Gutenberg-Richter
Legge di Gutenberg – Richter:
Log λm = a – bm
λm = 10(a-bm) = e(α-βm)
λm : numero di terremoti di magnitudo superiore ad m
verificatisi in un dato intervallo di tempo in una data area
(tasso di eccedenza)
a : 10a quantifica il numero di terremoti di magnitudo ≥ 0
b
log
λ
I valori a e b vengono ottenuti mediante
regressioni su data base sismico della
zona di interesse.
b: indica la frequenza di terremoti grandi o piccoli (al crescere
di b diminuisce il numero di forti terremoti rispetto ai piccoli)
• Normalmente b è compreso tra 2/3 e 1 e non mostra molta variabilità regionale. Il valore di b si differenzia in modo
significativo nelle sequenze sismiche in cui può arrivare a 2.5; questo indica che non ci sono terremoti di grande energia
per quell’episodio. Ciò si verifica spesso in aree vulcaniche dove, per la presenza di piccole faglie, l’accumulo della
deformazione è scaricato da piccoli terremoti.
Periodo di ritorno (TR):
TR = 1/λm
Pericolosità sismica: leggi di attenuazione
Una legge predittiva rappresenta sostanzialmente una legge che permette di prevedere un
parametro di scuotimento in funzione della magnitudo, della distanza e, in alcuni casi, anche
di altre variabili, per esempio
Y=f (M,R,P)
Dove Y è il parametro di scuotimento sismico di interesse, M la magnitudo, R la distanza
sorgente-sito considerata e P indica parametri variabili (sorgente, cammino dell’onda,
condizioni al sito).
Le leggi predittive si sviluppano attraverso delle regressioni del data-base sismico che si ha
a disposizione e possono essere aggiornate non appena un nuovo evento sismico diventa
disponibile.
Esiste una forma comune per le relazioni predittive che si basa sulle seguenti osservazioni:
•I picchi dei parametri di scuotimento strong motion hanno una distribuzione logaritmica
( ossia il logaritmo del paramtero si distribuisce linearmente). Quindi si avrà lnY
•La magnitudo viene espressa come il logaritmo di un parametro di scuotimento sismico.
Quindi lnY è proporzionale a M
•Durante il percorso sorgente-sito sono lo stress dell’ onda decade. In particolare l’ampiezza
delle onde di volume decresce secondo 1/R mentre per le onde superficiali l’ampiezza
decresce di circa 1/
R
•L’area di rottura delle faglia aumenta all’aumentare della magnitudo. Quindi R aumenta con
l’aumento della magnitudo.
Pericolosità sismica: leggi di attenuazione
1.
Parte dell’energia dell’onda sismica viene assorbita dal materiale che attraversa durante
la propagazione. Questo assorbimento fa si che l’ampiezza del movimento sismico
decresca esponenzialmente con R.
2.
I parametri di scuotimento sismico possono essere influenzati dalle caratteristiche della
sorgente (tipo di rottura) o dalle caratteristiche del sito (roccia/sedimenti)
Combinando tutte queste osservazioni si la tipica forma di una legge predittiva
lnY = C1 + C2 M+C3 MC4 + C5 ln[R +C6 exp(C7 M)] + C8 R + f(sorgente)+f(sito)
1
σ
ln Y
2
=C
9
3
4
5
6
Descrive l’incertezza del valore del parametro di scuotimento sismico
ricavato dalla legge predittiva. Statisticamente rappresenta la
deviazione standard del lnY alla magnitudo e distanza di interesse.
Pericolosità sismica: calcolo
Probabilistic Seismic Hazard Analysis (PSHA): it is a process that
integrates (aggregation) over aleatory uncertainties (e.g., future earthquake
locations, future earthquake magnitudes) to calculate the likelihood of
occurrence (or, alternatively, the probability of exceedance) of an earthquake
characteristic, Y, at a site during a given period of time (Cornell, 1968).
λ y* =
NS
∑ υ ∫∫∫ f
i= 1
i
Magnitude PDF
M
(m) f R (r ) P[Y > y* | m, r ]dmdr
Distance PDF
Attenuation Eq.
Y may indicate a ground motion parameter but also fault displacement
and slope displacement
Pericolosità sismica: incertezza
In PSHA epistemic uncertainties
are incorporated into calculations
through the use of logic trees.
Family of Hazard Curves
From McGuire (2004)
Pericolosità sismica: mappe
Le mappe di pericolosità sismica sono state
elaborate in termini di mediana della
distribuzione dei valori di pericolosità anziché
in termini di valori medi.
http://esse1.mi.ingv.it/
Pericolosità sismica in Italia
Spettri iso-probabili:
per una fissata probabilità di
eccedenza, esprimono i valori
accelerativi in funzione del periodo
spettrale a cui si riferiscono
Curve di Pericolosità:
esprimono il tasso medio annuo
di eccedenza di fissati valori di
scuotimento
Cataloghi sismici
INGV CPTI (1000-1980)
UniGe (1980-2010)
Terremoto di “Bussana” (1887)
Sismicità storica
Data
(Anno/Mese/Giorn
o)
1818/02/23
1819/01/08
1854/12/29
1887/02/23
Lat, Long
(UniGe)
Lat, Long
(INGV- CPTI04)
I0
Ms
Msp
43.74°N, 8.13°E
43.71°N, 8.06°E
43.63°N, 7.73°E
43.74°N, 8.13°E
43.920°N, 8.034°E
44.050°N, 8.200°E
43.820°N, 7.550°E
43.920°N, 8.070°E
VII - VIII
VI - VII
VII - VIII
IX
5.37
4.70
5.69
6.29
5.52
4.90
5.69
6.29
Sismicità
Storica
Strumentale
Incertezza
 Analisi delle incertezze attraverso “albero logico”:
• Due zonazioni sismogenetiche ;
• Quattro metodi per stimare i
parametri di ricorrenza di ogni zona
sismogenetica;
• Tre metodi per stimare la Mag max
per ogni zona sismogenetica;
• Due leggi empiriche di
attenuazione del moto sismico
(PGA);
Zonazioni Sismogenetiche
UniGe
INGV
Leggi di attenuazione della accelerazione di picco (PGA)
Ambraseys (1999)
Sabetta e Pugliese (1996)
Leggi di ricorrenza sismica per le zone sismogenetiche
Esempio di curve di pericolosità
λy* = numero di “eccedenze annue” in funzione del valore dello scuotimento
sismico (in questo caso l’accelerazione orizzontale di picco);
N.B: (1/λy* ) = Tempo di ritorno medio;
PGA = 0.125 => Tret = 100 anni
PGA = 0.245 => Tret = 1000 anni
Fascio di curve = Incertezza della stima delle curve di hazard associata alla
struttura dell’albero logico.
Mappe di pericolosità sismica in PGA
MRP: 475 anni (probabilità di eccedenze del 10% in 50 anni)
Mappe di pericolosità sismica in PGA
MRP: 975 anni (probabilità di eccedenze del 5% in 50 anni)
UniGe _MPS04 (MRP=475, Imperia)
Presente Studio
MPS04
50mo
84mo
percentile percentile
50mo
84mo
percentile percentile
Comuni
Longitudine
Latitudine
Media
Δ
Δ*
AIROLE
7.561
43.874
0.153
0.154
0.190
0.036
0.139
0.160
0.021
0.014
APRICALE
7.685
43.889
0.161
0.162
0.203
0.041
0.148
0.170
0.023
0.014
AQUILA DI ARROSCIA
7.997
44.092
0.131
0.132
0.166
0.035
0.128
0.146
0.018
0.004
ARMO
7.909
44.095
0.129
0.130
AURIGO
7.916
43.992
0.155
0.157
0.165
0.034
0.133
0.152
0.020
-0.003
0.198
0.041
0.150
0.173
0.023
0.007
BADALUCCO
7.821
43.921
0.162
0.163
0.204
0.041
0.155
0.179
0.024
0.008
BAIARDO
7.710
43.904
0.161
0.162
0.203
0.041
0.151
0.174
0.023
0.012
BORDIGHERA
7.675
BORGHETTO D’ARROSCIA
7.980
43.794
0.162
0.163
0.197
0.034
0.131
0.150
0.019
0.032
44.068
0.138
0.138
0.176
0.038
0.135
0.154
0.020
0.004
BORGOMARO
7.953
43.979
0.157
0.158
0.200
0.042
0.150
0.172
0.023
0.008
CAMPOROSSO
7.617
43.815
0.156
0.157
0.189
0.033
0.133
0.153
0.019
0.024
CARAVONICA
7.953
43.998
0.154
0.155
0.197
0.041
0.148
0.170
0.022
0.007
CARPASIO
7.858
43.960
0.158
0.160
0.201
0.042
0.154
0.178
0.024
0.005
CASTEL VITTORIO
7.736
43.942
0.160
0.161
0.203
0.042
0.154
0.178
0.024
0.007
CASTELLARO
7.868
43.874
0.166
0.167
0.207
0.040
0.149
0.172
0.023
0.018
CERIANA
7.772
43.884
0.163
0.165
0.205
0.040
0.151
0.174
0.023
0.014
CERVO
8.120
43.932
0.168
0.167
0.208
0.040
0.134
0.153
0.019
0.033
CESIO
7.972
44.015
0.152
0.152
0.194
0.041
0.145
0.167
0.022
0.007
CHIUSANICO
7.993
43.975
0.158
0.159
0.201
0.042
0.148
0.170
0.022
0.011
CHIUSAVECCHIA
7.980
43.960
0.160
0.161
0.203
0.042
0.148
0.170
0.022
0.012
CIPRESSA
7.929
43.854
0.170
0.170
0.209
0.039
0.142
0.162
0.021
0.028
CIVEZZA
7.952
43.875
0.168
0.168
0.208
0.040
0.143
0.165
0.021
0.025
COSIO DI ARROSCIA
7.787
44.098
0.133
0.133
0.170
0.036
0.135
0.156
0.020
-0.002
COSTARAINERA
7.935
43.862
0.169
0.169
0.209
0.040
0.143
0.164
0.021
0.026
DIANO ARENTINO
8.036
43.954
0.162
0.162
0.204
0.042
0.144
0.165
0.021
0.018
DIANO CASTELLO
8.065
43.926
0.166
0.166
0.207
0.041
0.141
0.161
0.020
0.025
DIANO MARINA
8.070
43.909
0.169
0.168
0.209
0.040
0.138
0.158
0.020
0.030
DIANO SAN PIETRO
8.058
43.953
0.163
0.163
0.205
0.042
0.142
0.163
0.021
0.021
DOLCEACQUA
7.609
43.869
0.157
0.158
0.195
0.037
0.141
0.162
0.021
0.017
Δ
UniGe _MPS04 (MRP=475, La Spezia)
Comuni
AMEGLIA
ARCOLA
BEVERINO
BOLANO
BONASSOLA
BORGHETTO DI VARA
BRUGNATO
CALICE AL CORNOVIGLIO
CARRO
CARRODANO
CASTELNUOVO MAGRA
DEIVA MARINA
FOLLO
FRAMURA
LA SPEZIA
LERICI
LEVANTO
MAISSANA
MONTEROSSO AL MARE
ORTONOVO
PIGNONE
PORTOVENERE
RICCO’ DEL GOLFO DI SPEZIA
RIOMAGGIORE
ROCCHETTA DI VARA
SANTO STEFANO DI MAGRA
SARZANA
SESTA GODANO
VARESE LIGURE
VERNAZZA
VEZZANO LIGURE
ZIGNAGO
Longitudine
Latitudine
Media
9.971
9.917
9.765
9.899
9.581
9.700
9.727
9.834
9.615
9.631
10.019
9.547
9.838
9.572
9.827
9.922
9.639
9.548
9.662
10.036
9.703
9.828
9.763
9.745
9.782
9.927
9.979
9.683
9.625
9.696
9.889
9.744
44.058
44.108
44.190
44.184
44.194
44.219
44.240
44.238
44.280
44.242
44.092
44.236
44.171
44.222
44.107
44.074
44.180
44.324
44.159
44.085
44.178
44.066
44.143
44.106
44.254
44.149
44.106
44.305
44.365
44.142
44.146
44.289
0.126
0.132
0.134
0.155
0.113
0.132
0.144
0.162
0.136
0.128
0.143
0.117
0.140
0.117
0.121
0.124
0.116
0.137
0.114
0.144
0.122
0.113
0.122
0.112
0.159
0.148
0.142
0.158
0.169
0.115
0.139
0.164
Presente Studio
MPS04
50mo
84mo
percentile percentile
0.130
0.141
0.137
0.148
0.138
0.149
0.162
0.171
0.116
0.129
0.137
0.147
0.149
0.160
0.169
0.179
0.140
0.151
0.132
0.144
0.149
0.159
0.120
0.133
0.145
0.155
0.120
0.133
0.124
0.136
0.127
0.139
0.119
0.132
0.142
0.153
0.117
0.130
0.149
0.160
0.125
0.137
0.116
0.129
0.125
0.137
0.115
0.128
0.166
0.176
0.154
0.164
0.147
0.157
0.165
0.175
0.177
0.187
0.117
0.130
0.145
0.155
0.172
0.182
50mo
84mo
Δ
percentile percentile
0.127
0.138
0.012
0.133
0.145
0.012
0.135
0.147
0.012
0.152
0.168
0.016
0.109
0.118
0.009
0.132
0.143
0.012
0.141
0.155
0.014
0.158
0.176
0.018
0.138
0.151
0.013
0.129
0.140
0.012
0.143
0.158
0.014
0.116
0.126
0.010
0.138
0.152
0.013
0.116
0.125
0.010
0.119
0.130
0.010
0.124
0.135
0.011
0.113
0.122
0.010
0.137
0.150
0.013
0.111
0.120
0.009
0.143
0.157
0.014
0.121
0.132
0.010
0.108
0.118
0.010
0.121
0.131
0.010
0.109
0.119
0.009
0.154
0.171
0.017
0.146
0.161
0.015
0.142
0.156
0.014
0.153
0.171
0.017
0.161
0.181
0.020
0.111
0.121
0.009
0.139
0.152
0.013
0.157
0.176
0.018
Δ
0.011
0.011
0.011
0.010
0.013
0.011
0.010
0.010
0.011
0.011
0.010
0.013
0.010
0.013
0.012
0.012
0.013
0.011
0.013
0.010
0.012
0.013
0.012
0.013
0.010
0.010
0.010
0.010
0.010
0.013
0.010
0.010
Δ*
0.003
0.004
0.004
0.010
0.007
0.005
0.008
0.011
0.003
0.004
0.006
0.004
0.006
0.004
0.005
0.003
0.006
0.005
0.006
0.007
0.004
0.008
0.004
0.006
0.012
0.008
0.005
0.012
0.016
0.006
0.006
0.014
Confronto tra mappe di PGA – UniGe e MPS4
 Si osservano modeste differenze tra UniGe e MPS4;
 Le maggiori differenze riguardano il ponente Ligure, soprattutto
in corrispondenza della costa imperiese (differenze mai superiori a
0.03g per MRP=475);
 In base all’Ordinanza PCM 3519 la maggior parte dei Comuni
liguri sarebbero classificati in Zona 3. Fanno eccezione alcuni
Comuni delle Province di Imperia, La Spezia e Savona che
rientrerebbero in zona 2.
Leggi di attenuazione della accelerazione spettrale SA
Spettri di risposta per D = 10 km
Spettri di risposta per D = 40 km
Mappe di pericolosità sismica in SA
MRP: 475 anni (probabilità di eccedenze del 10% in 50 anni)
Mappe di pericolosità sismica in SA
MRP: 975 anni (probabilità di eccedenze del 5% in 50 anni)
Confronto tra spettri isoporobabili – UniGe e MPS4
 Sono stati calcolati gli spettri isoprobabili per ogni punto
del territorio ligure e confrontati con quelli di MPS4
Confronto tra gli
spettri di risposta a
pericolosità uniforme
(valori mediani di
accelerazione
spettrale) calcolati nel
presente studio
(UniGe.) per un sito in
prossimità di Savona ed
i corrispondenti stimati
nell’ambito della
valutazione della
pericolosità sismica
italiana (MPS04).
Intensità Spettrale ASI
 L’intensità spettrale ASI è definità come:
ASI (ξ ) =
0.5
∫ S (η
a
0.1
= 0.05, T )dT
Confronto tra le stime di ASI – UniGe e MPS4
Provincia
ASI
Dip.Te.Ris.
0.1− 0.5
ASI
MPS04.
0.1− 0.5
.
.
ASI 0Dip.Te.Ris
.1− 0.5
ASI 0Dip.Te.Ris
.1− 1.0
ASI 0MPS04
.1− 0.5
ASI
MPS04.
0.1− 1.0
.
ASI 0Dip.Te.Ris
.1− 1.0
ASI 0MPS04
.1− 1.0
Genova
0.047
0.038
1.237
0.075
0.053
1.415
Imperia
0.096
0.068
1.412
0.145
0.100
1.450
Savona
0.045
0.032
1.406
0.072
0.042
1.714
La Spezia
0.081
0.065
1.246
0.126
0.097
1.299
Confronto tra i valori di
intensità spettrale
calcolati a partire dagli
spettri di risposta a
pericolosità uniforme (MRP
= 475 anni) ottenuti nel
presente studio (UniGe) e
nell’ambito del calcolo della
pericolosità sismica
nazionale (MPS04).
Confronto tra spettri di risposta isoprobabili
 Gli spettri isoprobabili ottenuti da UniGe risultano costantemente
più conservativi rispetto a quelli di MPS4;
 Le maggiori differenze di SA si riscontrano per periodi spettrali
maggiori di T=0.2 s e sono principalmente dovute all’utilizzo di una
zonazione sismogenetica alternativa.
GRAZIE