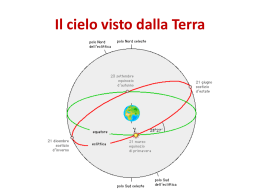
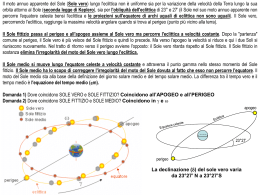
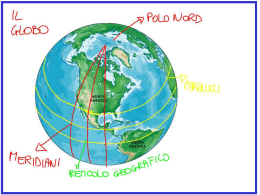
Mauro D’Onofrio
La rotazione della Terra come misura del tempo.
La misura del tempo può effettuarsi soltanto con la
considerazione di determinati movimenti; se per es. si ha a
disposizione un movimento esattamente uniforme, basta la misura
dello spazio percorso per la determinazione del tempo; dato che
allora vi é esatta proporzionalità tra percorso e tempo.
I moti che più si prestano a tale misura sono i moti angolari
astronomici, in particolare il movimento che più comunemente
appare ai nostri sensi, quello della Terra intorno al proprio asse,
movimento che si rispecchia per noi nella rotazione della sfera
celeste intorno all'asse del mondo e nel verso opposto a quello della
rotazione della Terra.
La velocità angolare di questo moto può riguardarsi ai fini del
problema che trattiamo come esattamente costante e così il moto
apparente della sfera celeste diviene il migliore ed il più comodo
misuratore del tempo che noi conosciamo.
Per effetto della rotazione della sfera, gli angoli orari dei punti
fissi sulla sfera variano ugualmente nello stesso intervallo di
tempo, ed in intervalli diversi variano di quantità proporzionali al
tempo.
É naturale perciò assumere come misura di intervallo di tempo
la quantità di rotazione della Terra avvenuta nell'intervallo
medesimo, e cioè 1’angolo che in quell'intervallo é descritto dal
cerchio orario di un determinato punto del cielo, che conviene
supporre situato sull'equatore celeste e che sarà l'indice mobile
insieme alla sfera. L'origine degli angoli orari essendo il meridiano
astronomico, e sull'equatore il mezzocielo é manifesto che 1’angolo
orario dell'indice predetto segnerà gli intervalli di tempo trascorsi
dal suo passaggio al mezzocielo, cioè segnerà il tempo a partire da
quell'istante
Si può dunque in generale definire il tempo come l'angolo
orario di un punto della sfera celeste. L'intervallo di tempo
corrispondente ad una intera rotazione della Terra si assumerà
come unità fondamentale per la misura del tempo.
Per quanto semplice sia la definizione di questa unità, non é
così facile fissarla praticamente.
Infatti, se l'asse della Terra fosse rigorosamente fisso nello
spazio e si potesse stabilire sulla sfera celeste un punto rigorosamente fisso, l'intervallo tra due successive culminazioni superiori
di questo punto in meridiano sarebbe l'unità predetta, ma né la
prima, né la seconda condizione é soddisfatta.
Giorno e tempo siderale.
Si conviene di assumere come unità astronomica per la misura
del tempo l’intervallo tra due successive culminazioni dell’equinozio
di primavera e si indica questa unità con il nome di giorno siderale.
Dati i piccoli movimenti dell'equinozio accennati, questa unità
non é assolutamente costante, né uguale all'unità fondamentale che
sarebbe il periodo di rotazione della Terra e quindi l'intervallo tra
due culminazioni di un punto fisso dell'equatore celeste; ma le
differenze sono cosi lievi, che il giorno siderale può considerarsi
praticamente come unità fondamentale.
Infatti la precessione é un lento movimento retrogrado
dell'equinozio per effetto del quale le ascensioni rette delle stelle
vanno generalmente crescendo con l'andar del tempo.
In un anno lo spostamento dell'equinozio sull'equatore é di
circa 46, cosicché, essendo 366,26 il numero di giorni siderali
contenuti in un anno, si ha
46
3.07s

 0.0084s
366.26 366.26
come differenza rispetto all'unità fondamentale.
Il giorno siderale ha principio all'istante della culminazione
dell’equinozio di primavera, ed é diviso in 24 ore siderali, l'ora
siderale in 60 minuti di tempo siderale, il minuto in 60 secondi di
tempo siderale.
Il tempo misurato coll'unità cosi definita e contato dall'istante
ora fissato, si identifica con l’angolo orario dell’equinozio di
primavera e si chiama perciò tempo siderale.
Tempo solare.
a) Tempo solare vero. Il giorno solare vero é l'intervallo di tempo
che trascorre tra due successive culminazioni (superiori o inferiori)
del Sole (centro del disco solare) in meridiano, o, più in generale, é
l'intervallo di tempo durante il quale l'angolo orario del Sole varia di
360°.
La culminazione superiore si dice anche mezzogiorno vero, la
culminazione inferiore mezzanotte vera.Il giorno solare viene diviso
analogamente al giorno siderale in 24 ore di tempo solare, ogni ora
in 60 minuti, ogni minuto in 60 secondi.
Si dice poi tempo solare vero di un luogo l'angolo orario del
Sole (centro), nel luogo stesso, aumentato di 12h , cioè l'angolo
orario contato dalla culminazione inferiore del Sole.
Il giorno siderale e il giorno solare vero sono di differente
durata, e ciò perché il Sole si sposta sulla sfera celeste in ogni giorno
di circa un grado, rispetto alle stelle fisse, nella direzione opposta al
moto diurno della sfera.
Il Sole arriva perciò ogni giorno con un certo ritardo rispetto
alle stelle in meridiano, ritardo che corrisponde al tempo impiegato
dal tratto descritto dal Sole a passare il meridiano, cioè a circa 4
minuti (di tempo siderale), equivalenti al grado sopraddetto, e perciò
il giorno solare vero é di circa 4 minuti più lungo di quello siderale.
Viceversa, una stella che in un dato giorno passa in meridiano
insieme al Sole, nel giorno successivo anticiperà il suo passaggio di
circa 4 minuti, per cui questo intervallo di tempo é stato chiamato
l'accelerazione delle stelle fisse.
L'indice che segna il tempo solare vero é propriamente
l'intersezione del circolo orario del Sole coll'equatore celeste. Per il
moto anzidetto del Sole fra le stelle, questo punto si sposta
sull'equatore nel senso delle ascensioni rette crescenti, ma il suo
moto non é uniforme, per cui il giorno solare vero non é una unità
costante.
Ciò avviene per due motivi - il primo é che la velocità angolare
del Sole nel suo moto intorno alla Terra, e quindi il suo moto
apparente sopra l'eclittica, é variabile; il secondo è che l'orbita
apparente del Sole, cioè l'eclittica, non coincide coll'equatore, ma è
inclinata su questo.
Con osservazioni continuate si riconosce che la velocità
angolare del Sole sull’eclittica è massima intorno alla longitudine
di 282°, e minima nella direzione opposta, cioè alla longitudine di
102°.
Nella prima di queste posizioni il Sole percorre al giorno
un arco di eclittica di 61’.1, che corrisponde a 4m 4s.
Nella seconda posizione il Sole percorre 57’.2, corrispondenti a 3m 49s. Cosicché, per il solo fatto del moto non uniforme sull’eclittica, il giorno solare sarebbe nel primo caso (che si verifica ai primi di gennaio) circa 15s più lungo che nel secondo caso
(che ha luogo al principio di luglio).
In altre parole, essendo cos  = 0.917, la variazione
dell'ascensione retta del Sole é agli equinozi di 1/12 minore della
variazione della longitudine ed ai solstizi di altrettanto maggiore.
Vedremo più tardi che la. variazione diurna media dell'ascensione retta del Sole è di 3m 57s ed altrettanto può dirsi per la
variazione media della longitudine (cioè facendo astrazione dalla
non uniformità del moto del Sole sopra l'eclittica): perciò la
variazione effettiva dell'ascensione retta del Sole vero, per il solo
fatto della obliquità, sarà intorno agli equinozi circa 4m 16s ed ai
solstizi circa 3m 37s al giorno. Per questo secondo fattore dunque il
giorno solare più lungo (agli equinozi) é di circa 39s più lungo del
giorno più corto dell'anno (ai solstizi).
I due fenomeni ora descritti si compongono in uno, ma dato che
essi sono spostati nel tempo (i massimi e i minimi non coincidono
alle stesse epoche), la differenza tra il giorno solare vero più lungo e
quello più corto arriva a circa 52s. Il primo ha luogo a metà
dicembre, il secondo alcuni giorni prima dell'equinozio d'autunno. Il
progressivo sommarsi di queste differenze in una serie di giorni
consecutivi conduce al fenomeno della equazione del tempo del
quale parleremo fra poco.
Per queste ragioni il tempo solare vero non può essere seguito
dai comuni orologi costruiti meccanicamente esso invece è indicato
dagli orologi solari, nei quali uno stilo, fissato in direzione parallela
all'asse della Terra su una superficie esposta al Sole, proietta la
propria ombra su questa superficie. Facendo passare per esso il
piano meridiano ed i piani orari 1h , 2h , …… prima e dopo del
meridiano e segnando le loro tracce sulla superficie, quando l’ombra
si troverà su una di queste, saranno appunto le ore 12, le 11 o le 13,
le 10 o le 14, ecc. di tempo solare vero locale.
Con un buon tempo solare medio
riuscirò ad evitare la
seconda parte!
Rotazione terrestre. - Ai fini pratici del nostro studio, si può dire
che la Terra ruota intorno al proprio asse polare in 23h 56m 45,091s.
Tale periodo é detto giorno sidereo o giorno siderale, ed é espresso
in tempo medio, cioè nel tempo usuale fornito dai nostri orologi
meccanici, regolati sui segnali orari trasmessi dagli Osservatori
Astronomici.
In seguito definiremo meglio tale tempo medio. Il giorno sidereo
si può quindi definire, con grandissima approssimazione, l'intervallo
di tempo compreso fra due passaggi consecutivi della medesima
stella al meridiano superiore di un luogo (culminazioni). A rigore,
l'intervallo sopra definito si denomina giorno stellare ed è di durata
pochissimo più lunga (23h 56m 4.099s); ed il giorno siderale propria-
mente detto (23h 56m 4.091s) è l'intervallo di tempo compreso fra 2
passaggi o culminazioni consecutive di un punto del cielo, non
contrassegnato da alcuna stella, e detto punto equinoziale di
primavera o punto  .Ci riferiamo ad una stella, perché in tal modo il
concetto di giorno siderale è più facile a comprendersi, e definiremo
fra breve tale punto . D'altra parte, la differenza fra giorno siderale
e giorno stellare è piccolissima (0.008s). Potremo anche dire che la
Terra ruota intorno al proprio asse polare in 24 ore siderali (quindi,
non 24 ore di tempo medio, o ore medie).
Già accennammo che l'asse di rotazione terrestre, idealmente
prolungato, incontra la sfera celeste in due punti, detti poli celesti.
Il punto del polo Nord celeste é situato presso una stella abbastanza
brillante (grandezza apparente 2,1 che é la stella «della Costellazione
dell'Orsa Minore» e detta perciò stella polare. Questa stella non
segna affatto il punto preciso del Polo nord celeste : la Polare è
lontana dal punto del Polo nord celeste 55' 54', cioè quasi il doppio
del disco lunare apparente. A causa di un moto particolare dell'asse
polare terrestre (moto di precessione degli equinozi) questa stella si
avvicinerà al Polo celeste fino all'anno 2105 (distanza minima 27'
42') poi tornerà ad allontanarsene regolarmente.
Se puntiamo una macchina fotografica
verso la Polare e lasciamo aperto lo
obiettivo per qualche ora, ogni stella
descrive per effetto del moto di rotazione della Terra, sulla sfera celeste un
cerchio (parallelo celeste), la cui
traccia, registrata dalla lastra fotografica, è un arco di cerchio; fra questi
cerchi è fondamentale quello il cui
piano passa per il centro della sfera
che si chiama equatore celeste. I paralleli e l’equatore visti dal Polo
Nord, sono percorsi dalle stelle (e da qualunque astro) in senso orario. L’equatore divide la sfera celeste in due emisferi: quello
boreale, nel quale si trova il Polo Nord celeste e quello australe,
contenente il Polo Sud (v. la 1a fig. della pag. che segue).
Le stelle prossime al Polo, nel punto più basso del loro giro,
sfioreranno l'orizzonte senza tramontare (tutte quelle che non
tramontano, per un certo orizzonte, sono dette perciò stelle
circumpolari per quel luogo) ; invece guardando verso l'orizzonte
Sud vedremo tutte le stelle sorgere, passare al meridiano Sud, e
tramontare (2a e 3a fig. della pag. successiva).
Come già accennato un osservatore sito al polo Nord
terrestre, avrà il Polo Nord
celeste al suo zenit; la stella polare quindi vicinissima allo zenit; e tutte le altre stelle visibili saranno circumpolari,
descrivendo in 24 ore siderali ciascuna un giro completo in un piano
parallelo all'orizzonte.
Analogamente al Polo Sud terrestre : ivi la polare é rappresentata
da una stellina di grandezza 5,8, quasi all'estremo limite della
visibilità a occhio nudo, ed é la stella  (sigma) della costellazione
dell' Ottante, che dista da quel polo circa 43'.
Equatore celeste.- Il piano dell’equatore terrestre, idealmente
prolungato, interseca la sfera celeste secondo un circolo massimo
detto equatore celeste il cui piano è quindi normale all’asse polare terrestre (detto in passato asse del Mondo).
Mezzocielo: è il punto della volta celeste in cui l’equatore celeste
taglia il meridiano del luogo, al di sopra dell’orizzonte.
Poiché l’altezza del Polo celeste sull’orizzonte è uguale alla latitudine del luogo (v. fig.), l’altezza del mezzocielo sarà: 90° - .
Z
Eclittica.- E’ l’orbita percorsa dal
centro della Terra nella sua rivoluzione annua intorno al Sole.
P
M

90°-
N
S
Secondo le apparenze la Terra è
immobile; e per l'osservatore terrestre sarà quindi il Sole che
sembrerà percorrere in un anno una propria orbita fra le stelle fisse,
sulla sfera celeste, tornando dopo circa 365 giorni e ¼ al suo punto
di partenza, cioè nella direzione di una medesima stella
lontanissima.
L'eclittica si definisce quindi anche: l'orbita apparente
descritta dal centro del Sole in un anno sulla sfera celeste, tra le
stelle fisse.
Il piano dell'equatore e il piano dell'eclittica sono inclinati fra
loro, formando un angolo di circa =23° 27' (obliquità dell'eclittica):
si dice anche che l'equatore é inclinato sull'eclittica di 23° 27' e
viceversa (v. fig.). Ciò dipende dal fatto che l'asse polare terrestre P,
P' non é perpendicolare al piano dell'orbita descritta dalla Terra, ma
é inclinato su di quello (piano dell'eclittica) di 66° 33" circa (v. fig.).
La obliquità dell'eclittica varia regolarmente, diminuendo di 46',84
per secolo, fino a raggiungere 21° 58' 36'', per poi risalire al
massimo di 24° 35' 58''.
PE
PC
P
Eclittica


Equatore
P’
Ecl.
Equinozio di primavera . - Allorché il centro del Sole nel suo moto
annuo apparente fra le stelle, lungo l'eclittica, taglia il piano
dell'equatore celeste passando dal Sud al Nord dell'equatore stesso,
si ha l'istante dell'equinozio di primavera; che si verifica sempre inintorno al glomo 21 Marzo. Ricordiamo però che si tratta non di un
giorno, ma di un preciso istante: e questa si potrà dire la definizione
temporale dell'equinozio. .
Il piano dell'equatore e quello dell'eclittica si intersecano secondo
una linea, detta linea equinoziale: chiamasi punto equinoziale di
primavera, o punto , il punto di intersezione, sulla sfera celeste,
dell'equatore celeste con l'eclittica, con Sole ascendente, cioè
passante dal Sud al Nord dell'equatore. Questa si potrà dire la
definizione sferico-geometrica dell'equinozio. Dunque l'equinozio di
primavera é un istante, ma è anche un punto ideale. ben definito
sulla sfera celeste. A 180° dal punto  - e cioè a 6 mesi di distanza,
considerato il moto del Sole - si ha l'altro estremo della linea
equinoziale, cioè l'equinozio di autunno (intorno al 23 Settembre)
con Sole discendente, ossia passante da Nord a Sud del piano
equatoriale.
Coordinate sferiche. - È bene premettere che la parola posizione di
un astro S non indica la sua posizione spaziale, che, per essere
precisata rispetto ad una determinata terna di assi cartesiani X,
Y, Z, richiede la conoscenza di tre numeri x, y, z, che
rappresentano le sue coordinate rettilinee (v. fig.).
La determinazione della
posizione spaziale implica,
evidentemente, la conoscienza della direzione OS
e della distanza d dell’astro
S dall’origine. Ma per i
corpi celesti in generale in-
teressa particolarmente la direzione in cui sono visti dall'osservatore
da un punto qualunque dello spazio e interessano le variazioni, col
tempo, di questa direzione.
Così, per es., dell'astro S interessa definire la direzione OS, indicata
dal punto S' sulla sfera. A questo scopo si consideri il cerchio
massimo corrispondente al piano XY e il suo polo Z, e si tracci il
cerchio massimo che unisce Z con S'. Come coordinate sferiche di S'
si assumono le ampiezze degli archi XS" e S"S', le quali sono
sufficienti a definire la posizione di S' sulla sfera celeste e quindi la
direzione OS.
L'ampiezza dell'arco XS" dipende, evidentemente, dalla scelta del
cerchio massimo fondamentale XY, dell'origine X su di esso e del
senso (orario oppure antiorario, secondo i casi) in cui il cerchio
fondamentale si suppone descritto, visto da Z; l'ampiezza dell'arco
S"S' è assunta sempre positiva quando l'arco si trova nell'emisfero a
cui appartiene il polo Z prescelto; negativa quando l'arco si trova
nell'emisfero opposto.
Sistemi di riferimento. Finora conosciamo tre cerchi massimi
fondamentali: l'orizzonte (che varia col luogo di osservazione),
l'equatore celeste e l'eclittica.
Ad essi è conveniente associare un altro cerchio massimo, l'equatore
galattico, assai utile nello studio dei problemi riguardanti la struttura
dell'Universo in generale, e in particolare del sistema di stelle della
Via Lattea ( «Galassia »).
La Via Lattea, che appare come una fascia luminosa che assai
irregolarmente cinge il cielo secondo un cerchio massimo, non è che
l'effetto di un enorme concentramento prospettico di stelle, di
ammassi e di nubi stellari. L'equatore galattico è l'intersezione della
sfera celeste col piano di simmetria della Via Lattea e risulta
inclinato di 62° sull'equatore celeste (v. fig.).
Sono molto importanti anche le quattro direzioni normali ai piani dei
suddetti cerchi fondamentali, c cioè, rispettivamente: la verticale,
l'asse di rotazione della Terra, l'asse dell'eclittica e l’asse galattico
(che è l'asse di rotazione del sistema della Via Lattea). Ognuna di
queste direzioni taglia la sfera celeste in due punti (detti poli del
cerchio fondamentale corrispondente) e fra essi se ne sceglie uno,
che ordinariamente si chiama il polo del cerchio stesso: abbiamo
così quattro poli fondamentali: lo zenit, il polo celeste nord, il polo
dell'eclittica e il polo galattico.
Questi cerchi massimi e i poli corrispondenti sono utili per definire
cinque importanti sistemi di coordinate, a cui, secondo i casi,
conviene riferire le posizioni degli astri sulla sfera celeste:
1.- Il primo sistema (detto azimutale) è strettamente connesso col
luogo di osservazione e serve per lo studio dei moti apparenti degli
astri, in relazione col luogo da cui si osservano. E’ già stato oggetto
di studio nei paragrafi precedenti.
2.- Il secondo sistema (detto orario) è pure legato al luogo di
osservazione: ha come cerchio fondamentale l'equatore e come
origine il punto d'intersezione col meridiano, situato al disopra
dell'orizzonte, detto mezzocielo . Anche questo sistema è già stato
illustrato
3.- Il terzo sistema (detto equatoriale) non ha, a differenza dei due
primi sistemi, alcun legame col moto rotatorio terrestre,. Il cerchio
fondamentale è ancora l'equatore celeste, ma esso è supposto
percorso in senso antiorario e l'origine scelta è l'equinozio di
primavera o punto gamma (v.fig. precedente). Le coordinate si
chiamano ascensione retta (simbolo ) e declinazione (simbolo ).
4.Il quarto sistema (detto
dell’eclittica) ha le medesime
caratteristiche del terzo sistema ed è pure indipendente
dal moto rotatorio terrestre. Il
cerchio fondamentale è la
eclittica, supposta descritta
in senso antiorario, e l’origine è l’equinozio di prima-.
vera Le coordinate si chiamano longitudine e latitudine
celesti. Sull’eclittica, oltre i
due equinozi (dì primavera e di autunno), occorre ricordare altri due
punti, pure diametralmente opposti, a 90° dagli equinozi : il solstizio
d'estate, E, a 90° dall'equinozio di primavera, e il solstizio d'inverno,
I. Il Sole, che noi vediamo sempre proiettato sull'eclittica, si trova
nei solstizi quando la sua declinazione raggiunge il massimo valore
assoluto, pari all'obliquità dell'eclittica. L'obliquità dell'eclittica
cambia lentamente col tempo .
5.- Il quinto sistema (detto galattico), pure indipendente dal moto
rotatorio terrestre, ha come cerchio fondamentale l’equatore
galattico, percorso in senso antiorario. Esso taglia l’equatore celeste
nel punto N avente 280° di ascensione retta, ed è inclinato di 62° (v.
fig.). Le coordinate si chiamano longitudine e latitudine galattica.
Sistema
Cerchio fondamentale
Origine delle coordinate
sferiche
Punto Sud
Nome delle coordinate
1°
Azimutale
2°
Orario
Orizzonte
(senso orario)
Equatore celeste
(senso orario)
Mezzocielo
Angolo orario
Declinazione
(simbolo )
Ascensione retta
(simbolo )
Declinazione
(simbolo )
Longitudine
Latitudine
(celesti)
Longitudine
Latitudine
(celesti)
3°
Equatoriale
Equatore celeste
(senso antiorario)
Equinozio
di primavera
(punto gamma)
4°
Eclittico
Eclittica
(senso antiorario)
5°
Galattico
Equatore galattico
(senso antiorario)
Equinozio
di primavera
(punto gamma)
Punto con
 = 280° ,  = 0°
Azimut e Altezza
Z
P
M
E
N


H
S
h
Az
W
B
fig. 1
Coordinate altazimutali. Si chiamano piani verticali quelli che
giacciono sulla verticale. Essi individuano sulla sfera celeste i cerchi
verticali. Tra questi é importante il primo verticale, quello che passa
per i punti E e W.
Per individuare un punto A sulla sfera celeste bisogna tracciare un
cerchio massimo passante per lo zenit Z e per A; esso interseca
l'orizzonte in B.
Le due coordinate sono:
- L’azimut Az, cioè l’angolo SOB, o
l’arco SB, misurato da sud verso
ovest, in senso orario, da 0° a 360°.
- L’altezza h, cioè l’angolo BOA o
l’arco BA contato da 0° a 90° partendo dall’orizzonte verso Z.
I punti posti sotto l'orizzonte hanno altezza negativa.
In marina e in geodesia l'azimut si misura partendo da nord in senso
orario.
Si dicono almucantarat i cerchi minori formati dai punti che hanno
uguale altezza.
La distanza zenitale z è l'arco ZA uguale a 90° - h.
La latitudine astronomica , sappiamo, è l’altezza del polo P, cioè
l’angolo NOP.
Il sistema orario La direzione e il piano fondamentale in
questo sistema sono:
• L’asse del mondo OP.
• Il piano equatoriale, cioè il
piano passante per O e perpendicolare all'asse OP. Esso determina sulla sfera celeste un cerchio
massimo detto equatore celeste.
La latitudine è quindi la distanza zenitale dell'equatore misurata
lungo un meridiano.
L'equatore interseca il cerchio dell'orizzonte nei punti E e W e
attraversa il meridiano nel punto M detto mezzocielo.
I cerchi massimi passanti per P diconsi cerchi orari. Uno di essi è il
meridiano NPZMS.
Sia sulla sfera celeste un punto A del quale si vuole stabilire la
posizione.
Per A si fa passare un cerchio orario che interseca in B l'equatore
celeste.
Le coordinate di A sono:
- L'angolo orario H, cioè l'angolo che PAB forma col meridiano
PZM (o l'arco MB). Esso si conta in ore, da 0 a 24, in senso orario,
cioè negativo, per un osservatore boreale O.
- La declinazione  o D, cioè l'angolo BOA o l'arco BA si conta da
0° a 90° partendo dall'equatore; positiva verso il polo celeste nord
(che é quello in corrispondenza del polo nord terrestre), negativa
verso sud.
Si chiama parallelo celeste il cerchio minore i cui punti hanno tutti
la stessa declinazione.
Durante la giornata le coordinate altazimutali di un punto fisso sulla
sfera celeste variano ambedue; nel sistema orario invece cambia solo
l'angolo H.
Dicesi culminazione superiore o inferiore il passaggio di un astro
rispettivamente al meridiano superiore o all'inferiore.
Il moto diurno, per un osservatore boreale che guarda a sud, si
svolge in senso retrogrado o negativo, cioè secondo le lancette
dell'orologio.
La condizione perché una stella sia circumpolare boreale per un
osservatore che ha il polo boreale sopra l'orizzonte è, come si ha
dalla fig.1, che la distanza polare sua sia minore o tutt'al più uguale
all'altezza del polo, cioè si deve avere
d 
90° - 
Per un luogo con altezza del polo o latitudine di 60° le stelle con
declinazione uguale o superiore a 30° saranno dunque circumpolari,
ed una stella di declinazione -30° o più australe resterà sempre
invisibile.
Gli astri di declinazione variabile, come ad es. il Sole, per
latitudini basse e medie si comportano come una stella oraria,
presentando l’arco diurno e notturno, mentre per latitudini alte
possono diventare circumpolari.
In pratica i fenomeni ora detti vengono leggermente modificati
per il fenomeno della rifrazione atmosferica, il quale fa apparire gli
astri ad un'altezza leggermente maggiore della vera sull'orizzonte,
con effetto crescente dallo zenit, dove è nullo, all'orizzonte, dove é
massimo. Per lo stesso motivo il metodo ora detto di determinare la
latitudine del luogo e la declinazione della stella ha l'inconveniente
di richiedere correzioni abbastanza forti e non sempre ben
determinate.
Quando sia nota l'altezza del polo, basta osservare la distanza
zenitale di una stella nella culminazione superiore (nella quale la
rifrazione ha generalmente poca influenza e quindi le correzioni
relative sono piccole) per averne la distanza polare d = 90° -  z; in
questa relazione vale il segno superiore per le stelle che culminano a
Sud dello zenit, quello inferiore per stelle che culminano a nord, fra
zenit e polo.
Nascere e tramontare degli astri
I due gruppi (1) e (2) servono a risolvere parecchi problemi, tra
i più importanti dei quali sono da nominarsi quelli riguardanti il
nascere e il tramontare degli astri.
Sia ad esempio conosciuta l'altezza polare  per un dato luogo
e la declinazione  di una stella, e sia richiesto l'angolo orario per il
nascere ed il tramontare della stella; essendo h = 0 al nascere o al
tramontare, segue dalla prima formula del gruppo (2):
0 = sen  sen  + cos  cos  cos H0
e quindi
cosH0 = -tg tg.
(3)
Supposto dapprima tg tg  <1, dei due valori reali di H0
che risultano in generale da questa relazione, uguali in valore
assoluto ma di segni contrari, quello negativo appartiene al nascere,
quello positivo appartiene al tramonto dell'astro ; il valore assoluto
predetto o, più precisamente, il valore di H0 compreso fra 0 e 180°
risultante dalla (3), non è altro che il semiarco diurno dell'astro.
Se  e  hanno lo stesso segno, il cosH0 è negativo ed i due
valori dell'angolo H0 appartengono al secondo ed al terzo quadrante
(rispettivamente per il tramontare ed il nascere), il che significa che
dal nascere al tramontare il cerchio orario dell'astro descrive un
angolo maggiore di 12h, cioè la stella ha un arco diurno maggiore
dell'arco notturno. L'opposto avviene quando  e  hanno segni
contrari.
Per un astro di declinazione variabile possono mutare anche le
condizioni della sua visibilità dette prima.
Per il Sole, che nel corso di un anno varia appunto la sua
declinazione passando da posizioni boreali a posizioni australi e
viceversa, e precisamente ha per una metà dell'anno  > 0, e per
l'altra metà  < 0, si trova che per tutti i luoghi deI1'emisfero
boreale, avendosi  > 0, quando é  > 0 i giorni (archi diurni dei
Sole) devono essere più lunghi delle notti (semestre estivo), e
quando è  < 0 i giorni saranno più brevi delle notti (semestre
invernale); per l'emisfero australe invece é  < 0 e quindi avviene
l'opposto.
Alla massima, rispettivamente alla minima declinazione del
Sole corrisponde evidentemente nel nostro emisfero - e fino ad una
certa latitudine che sarà precisata fra poco - la. durata massima,
rispettivamente, minima del giorno.
Il giorno più lungo dell'anno alle diverse latitudini  risulta
facilmente dalla (3) per la declinazione massima raggiunta dal Sole 
= + 23° 27', con il che si ha
cos H0 = - 0.434 tg ,
Anche i fenomeni del nascere e tramontare degli astri sono
influenzati dalla rifrazione astronomica, la quale causa per i punti in
vicinanza dell’orizzonte un apparente aumento di altezza di circa
mezzo grado, che anticipa il nascere e ritarda il tramonto.
Le formule di trasformazione tra il primo ed il secondo sistema
di coordinate servono anche alla determinazione della posizione del
punto sull'orizzonte in cui nasce o tramonta un astro, posizione data
mediante l’azimut corrispondente A0.
Si ha infatti facilmente dalla prima relazione del gruppo (1) per
h = 0 e rispettivamente per h = - 0° 35':
cos A0 = - sen  sec 
cos A’0 = - sec 35' sen  sec  - tg 35' tg 
(4)
ed anche qui, come nel caso di H0, se da queste relazioni risultano
valori reali di A0 o di A’0, quello appartenente al terzo o quarto
quadrante riguarda il nascere e quello appartenente al primo o
secondo riguarda il tramonto.
Dalla (4) si vede che i punti del nascere e del tramontare sono
rispettivamente nel terzo e secondo quadrante quando declinazione è
positiva e nel quarto e primo quando é negativa, il che vuol dire che
gli astri di declinazione boreale nascono e tramontano a nord dei
punti di vero oriente e vero occidente, quelli di declinazione invece
nascono e tramontano a sud di questi punti.
ASIAGO
Sistema equatoriale e puntamento
Il punto gamma costituisce l'origine degli archi sull'equatore. Il
sistema in tal modo è legato alla sfera celeste indipendentemente dal
suo moto attorno alla Terra. Le coordinate degli astri legati a essa
non cambiano quindi nell'arco dell'anno.
Un punto A sulla sfera celeste viene individuato nel seguente
modo. Per A si fa passare un cerchio orario che interseca in B
l'equatore (v. fig.).
Le coordinate equatoriali di A sono:
L'ascensione retta AR o : cioè l'angolo, misurato in ore, da 0 a
24, in senso positivo (antiorario) dal punto  verso B.
La declinazione D o  è definita come nel sistema precedente.
Si dice tempo siderale t l'angolo orario del punto gamma (v.
fig.).
Poiché l'angolo orario H di un astro si conta in senso contrario a
quello dell'ascensione retta  vi è la relazione:
t=a+H
Nota l'ascensione retta di una stella, misurando il suo angolo
orario, si trova subito il tempo siderale (v. fig.).
Osservando il transito di un astro al centro del campo di un
telescopio capace di ruotare solo lungo il meridiano superiore, si può
determinare l'ascensione retta leggendo, contemporaneamente, il
tempo siderale t.
Infatti essendo al meridiano H = 0° si ha:
=t
Le coordinate equatoriali del Sole all'inizio delle varie stagioni
(v. fig.) sono le seguenti:
Primavera (21 mano)  = 0h;  = 0°
Estate (22 giugno)  = 6h;  = + 23°,5
Autunno (23 settembre)  = 12h;  = 0°
Inverno (22 dicembre)  = 18h;  = - 23°,5.
Un telescopio montato nel modo appena detto si chiama
cerchio meridiano.
Un telescopio capace di ruotare attorno a due assi perpendicolari tra
loro, uno dei quali é diretto sul polo celeste (asse polare), consente
di seguire il moto degli astri con la semplice rotazione dell'asse
polare operata da un preciso movimento a orologeria (moto orario).
Questo tipo di montatura si dice equatoriale.
I due assi di rotazione si chiamano: asse orario o polare quello
puntato sul polo celeste, asse di declinazione l'altro.
Due cerchi graduati, ben tarati, posti sui due assi consentono di
puntare il telescopio su un qualunque astro del quale siano note le
coordinate equatoriali  e .
Per il puntamento basta ruotare lo strumento attorno all'asse di
declinazione fino a che sul cerchio graduato corrispondente si legge
il valore di . Poi, letto su un orologio il tempo siderale t, si ruota
l'asse orario di un angolo H= t -  che si legge sul cerchio graduato
delle ascensioni rette, il cui zero è in corrispondenza del meridiano
locale.
1 cataloghi che elencano gli oggetti celesti riportano
l'ascensione retta e la declinazione dei vari astri, stabilita per un
certo anno. Vedremo infatti che le coordinate equatoriali cambiano,
seppure lentamente, a causa del fenomeno della precessione degli
equinozi.
Per il controllo del tempo siderale vengono utilizzate certe
stelle dette fondamentali le cui posizioni sono determinate con
grande precisione.