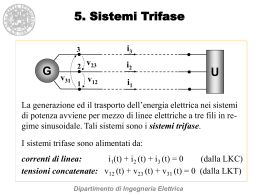
Principi di ingegneria elettrica
Lezione 15a
Sistemi trifase
Teorema di Boucherot
La potenza attiva assorbita da un bipolo è uguale alla somma
aritmetica delle potenze attive assorbite dagli elementi che lo
compongono.
La potenza reattiva assorbita da un bipolo è uguale alla somma
algebrica delle potenze reattive assorbite dagli elementi che lo
compongono.
La potenza complessa assorbita da un bipolo è uguale alla
somma vettoriale delle potenze complesse assorbite dagli
elementi che lo compongono.
Teorema di Boucherot
In base al principio di conservazione delle potenze, attiva e
reattiva, i bipoli assumono le seguenti proprietà.
1. I bipoli costituiti esclusivamente da induttori e condensatori
sono reattivi:
Pk = 0 ⇒ P = ∑ Pk = 0 ⇒ Re[Z] = R = 0
k
2. I bipoli costituiti esclusivamente da resistori e induttori sono
induttivi:
per i resistori : Qk = 0; per gli induttori : Qk > 0
Q = ∑ Qk > 0 ⇒ Im[Z] = X > 0
k
3. I bipoli costituiti esclusivamente da resistori e condensatori sono
capacitivi:
per i resistori : Qk = 0; per i condensatori : Qk < 0
Q = ∑ Qk < 0 ⇒ Im[Z] = X < 0
k
Reti a scala
È particolarmente conveniente applicare il teorema di Boucherot nelle
reti a scala formate da impedenze in serie, alternate con ammettenze
in parallelo.
Note le impedenze e le condizioni di funzionamento del carico finale
(tensione, potenza attiva, potenza reattiva) si ricavano le condizioni di
funzionamento della sezione iniziale in base a semplici calcoli di
natura algebrica nel campo dei numeri reali).
La rete viene suddivisa in sezioni contenenti ciascuna una sola
impedenza.
Si parte dalla sezione finale (a) e si determinano: i moduli di tensione
e corrente e le potenze attiva e reattiva.
Risalendo a monte si incrementano per ogni sezione i valori della
potenza attiva e di quella reattiva, per rivalutare il modulo della
tensione o della corrente.
Sezione finale
Parametri noti: tensione (V), potenza attiva (P), potenza reattiva (Q).
Si calcola il valore della corrente.
S
I=
V
Tratto a-b
Parametri noti: impedenza Z3S = R3S + j X3S
Si calcolano potenza attiva e reattiva.
P3 S = R3 S I 2
Q3S = X 3 S I 2
Sezione b
Parametri noti: potenza attiva (P), potenza reattiva (Q).
Si compongono le potenze e si calcola la tensione Vb
Pb = P + P3 S
Sb = Pb + Qb
Qb = Q + Q3S
Ib = I
2
2
Vb =
Sb
Ib
Sezione c
Parametri noti: ammettenza Y2P = G2P + j B2P
Si calcolano potenza attiva (P2P) e reattiva (Q2P) e la corrente Ic.
Vc = Vb
P2 P = G2 PVc
2
Q2 P = B2 PVc
2
Pc = Pb + P2 P
Qc = Qb + Q2 P
Sc = Pc + Qc
2
Ic =
Sc
Vc
2
Bipoli passivi
Bipolo passivo è un bipolo caratterizzato da:
P≥0
cos ϕ =
P
≥ 0 ⇒ − 90° ≤ ϕ ≤ +90°
S
bipoli resistivi
bipoli reattivi
bipoli induttivi
bipoli capacitivi
X = 0 ⇒ Q = 0 ⇒ cos ϕ =
R = 0 ⇒ P = 0 ⇒ cos ϕ =
P
= 1 ⇒ ϕ = 0°
S
P
= 0 ⇒ ϕ ± 90°
S
X > 0 ⇒ Q > 0 ⇒ 0° < ϕ ≤ 90°
X < 0 ⇒ Q < 0 ⇒ − 90° ≤ ϕ < 0°
Fattore di potenza
Il fattore di potenza viene utilizzato per caratterizzare il comportamento
energetico di un circuito passivo.
Il cosϕ non dipende dal segno dell’angolo ϕ : cos(ϕ) = cos(-ϕ).
Per distinguere i due casi si deve specificare se il fattore di potenza è
da intendersi in ritardo (-ϕ) oppure in anticipo (ϕ) di fase.
I termini ritardo e anticipo si riferiscono alla fase della corrente rispetto
alla tensione.
Corrente in ritardo:
bipolo induttivo
Corrente in anticipo:
bipolo capacitivo
Rifasamento
La resistenza di una linea di trasmissione in generale non è trascurabile.
Per esempio, un cavo di alluminio di diametro 1cm ha una resistenza di circa
2·10-4 Ω/m. Se il cavo è lungo 10 km presenta una resistenza di circa 2 Ω.
VS = V + 2Rl I l
La differenza tra V e VS cresce all’aumentare dell’ampiezza della corrente di
linea.
Aumentando la corrente di linea aumenta la dissipazione di potenza sulla linea di
trasmissione.
Pd = 2Rl I l2,eff
Rifasamento
È possibile diminuire la potenza dissipata in linea, aumentando la sezione dei
cavi oppure riducendo, a parità di potenza attiva trasmessa, l’ampiezza della
corrente di linea.
Pu = Veff I l ,eff cos ϕ
Condensatore di rifasamento
Il problema consiste nel determinare il valore della capacità C
necessaria per ridurre l’angolo da ϕ1 a ϕ2 .
1
QC = − ωCVm2 = −ωCVeff2 < 0
2
Q2 = Q1 + QC < Q1
Q1 = Pu tan ϕ1
Q2 = Pu tan ϕ2
QC = Q1 − Q2 = Pu (tan ϕ1 − tan ϕ2 )
C=
QC
ωVeff2
C0 =
=
Pu (tan ϕ1 − tan ϕ2 )
ωVeff2
Pu tan ϕ1
ωVeff2
Rifasamento totale
Sistemi trifase
L’energia elettrica viene generalmente prodotta, trasmessa e
distribuita (alle grandi utenze) secondo la disposizione circuitale
trifase.
I sistemi trifase presentano una maggiore efficienza rispetto ai
sistemi monofase di potenza equivalente:
minor peso dei conduttori e degli altri componenti
trasferimento di potenza costante (se il carico elettrico è
costante i generatori richiedono una potenza meccanica
all’asse continua, non di tipo oscillante )
Sistemi trifase
Un generatore di tensione monofase (alternatore) è costituito da due parti
coassiali: una parte fissa, detta statore, e una parte rotante detta rotore.
Il rotore può essere un magnete permanente oppure un avvolgimento percorso
da corrente continua che genera un campo magnetico costante nel tempo.
Lo statore è un cilindro cavo sulla cui superficie interna sono ricavate delle cave
in cui sono alloggiate le spire dell’avvolgimento di statore.
Sistemi trifase
Il rotore è conformato in modo tale che il flusso dell’induzione magnetica
concatenato con l’avvolgimento fisso sia una funzione sinusoidale dell’angolo
di rotazione θ.
Φ = Φ m sin(θ )
Il rotore gira a velocità angolare costante ω, quindi il flusso varia nel tempo
con legge sinusoidale
Φ (t ) = Φ m sin(ωt )
Per la legge di Faraday, ai capi dell’avvolgimento di statore verrà indotta una
tensione pari a
dΦ
vaa' (t ) =
= ωΦ m cos(ωt )
dt
La frequenza è di norma 50 Hz (ω=100π) ad essa corrisponde per una
macchina ad una sola coppia polare una rotazione di 3000 giri al minuto.
Quando viene collegato un carico elettrico al generatore, questo eroga una
potenza variabile nel tempo (in modo oscillatorio).
La natura oscillatoria della potenza produce vibrazioni meccaniche che
rendono problematica la costruzione di generatori monofase di potenza
elevata.
1
1
p (t ) = Vm I m cos(θ v − θ i ) + Vm I m cos(2ωt + θ v + θ i )
2
2
Nel generatore trifase la disposizione spaziale
degli avvolgimenti di ciascuna fase, disposti a
120°, determina flussi concatenati anch’essi
sfasati l’uno rispetto all’altro di 120°
Di conseguenza le tre tensioni indotte sono sfasate di 120°
Le tre tensioni hanno stessa ampiezza e frequenza, ma fasi diverse, da cui il
nome di generatore trifase.
Sistemi trifase
Trascurando l’impedenza propria degli avvolgimenti, il generatore trifase si
può schematizzare con tre generatori sinusoidali collegati a stella.
Sistemi trifase
Naturalmente si può passare alla notazione fasoriale
Sistemi trifase
Circuiti trifase
Lo schema generale di un circuito trifase è costituito da un generatore trifase
collegato tramite una linea trifase ad un carico trifase.
Va
Vc
Vb
Le tensioni tra i conduttori della linea sono dette tensioni di linea o tensioni
concatenate. Applicando la LKT si ha:
Circuiti trifase
Quindi anche le tensioni di linea costituiscono una terna simmetrica di
tensioni:
Circuiti trifase
Si chiamano correnti di linea le correnti assorbite dal carico.
Per la LKC si ha in generale:
Circuiti trifase
Le configurazioni utilizzate per il carico sono prevalentemente due:
il carico a stella
il carico a triangolo
Circuiti trifase
Carico a stella
Nella configurazione a stella le correnti di fase coincidono con le correnti di linea.
Il calcolo delle correnti risulta particolarmente semplice utilizzando l’analisi
nodale scegliendo come nodo di riferimento il centro-stella
Va
Vc
Vb
Carico a stella
Il centro-stella del carico si trova allo stesso potenziale del centro-stella dei
generatori: tra n e n’ esiste un corto circuito virtuale
Va
Vc
Vb
Carico a stella
Le tensioni di fase coincidono con le tensioni dei tre generatori e le correnti di
linea si ricavano facilmente con la legge di Ohm
La terna delle correnti di linea è ruotata di un angolo –ϕ rispetto alla terna delle
tensioni di fase.
Carico a stella
Poiché:
Ia =
Va
ZL
Ib =
Vb
ZL
Ic =
Vc
ZL
Si può affermare che il circuito trifase equivale a tre circuiti monofase
indipendenti
Carico a stella con impedenze di linea
Tenendo conto delle impedenze di linea:
Carico a triangolo
Nella configurazione a triangolo le tensioni di fase coincidono con le tensioni di
linea.
Il calcolo delle correnti di fase risulta particolarmente semplice utilizzando la
legge di Ohm.
Le correnti di linea si ricavano applicando la KLC ai tre vertici del triangolo.
Ia
a
Va
Vc
Vb
Ib
Ic
b
Ica
c
Carico a triangolo
Carico a triangolo
Nel caso di carico equilibrato conviene ricorrere alla trasformazione triangolostella.
Va
Vc
Vb
Potenza assorbita da un carico 3f equilibrato
La potenza istantanea assorbita da un bipolo in regime sinusoidale è:
Carico equilibrato a stella
Un generatore trifase che alimenta carichi equilibrati eroga una potenza
istantanea costante, anziché pulsante come nel caso monofase.
Espressione generale della potenza
Nel caso di carico equilibrato a triangolo vale lo stesso risultato, poiché un
triangolo equilibrato equivale sempre ad una stella equilibrata.
Nel caso del carico a stella:
V fC =
Vl
3
I fC = I l
P = 3 V fC I fC cos ϕC = 3 Vl I l cos ϕC
Nel caso del carico a triangolo:
V fC = Vl
I fC =
Il
3
P = 3 V fC I fC cos ϕC = 3 Vl I l cos ϕC
In entrambi i casi:
Q = 3 V fC I fC sin ϕC = 3 Vl I l sin ϕC
S = 3 Vl I l (cos ϕC + j sin ϕC )
S = 3 Vl I l
cos ϕC =
P
S
Confronto monofase-trifase
Confrontiamo il sistema trifase rispetto al monofase considerando uguali:
Circuiti trifase con neutro
Rifasamento di un carico trifase
Rifasamento di un carico trifase
CT =
CS
3
Massimo trasferimento di potenza
Massimo trasferimento di potenza
Massimo trasferimento di potenza
Sovrapposizione della potenza
starter
V = 230 V
P = 65 W
VL= 110 V
XL= 342 Ω
I = 0,591 A
Tubo fluorescente
cosϕ = 0,478
cosϕR = 0,9
C = 5,3 µF
reattore
Schema di alimentazione di una lampada fluorescente