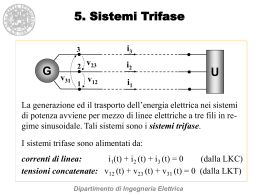
Sistemi trifase
1
Generalità
Si consideri un supporto cilindrico (armatura) (figura 1) alla cui periferia siano collocate, in corrispondenza dei piani
diametrali, tre bobine aventi rispettivamente
, , spire e disposte in maniera che, percorrendole dai terminali
iniziali 1p, 2p, 3p ai terminali finali 1f, 2f, 3f risultino avvolte, rispetto all’armatura, tutte nello stesso senso.
Se l’armatura ruota con velocità angolare costante in un campo magnetico costante nel tempo e con distribuzione
spaziale qualsiasi, si generano nelle bobine tre f.e.m., di tipo mozionale, periodiche che hanno tutte lo stesso periodo,
la stessa forma d’onda e risultano sfasate nel tempo, l’una rispetto all’altra, di un angolo pari all’angolo di sfasamento
spaziale fra gli assi delle bobine cablate sull’armatura.
Figura 1
Se invece l’armatura ruota con velocità angolare costante in un campo costante nel tempo ed avente distribuzione
spaziale uniforme, le f.e.m. indotte sono sinusoidali isofrequenziali e risultano sfasate nel tempo, l’una rispetto
all’altra, di un angolo pari all’angolo di sfasamento spaziale fra gli assi delle bobine cablate sull’armatura
240°
120°
Se poi le bobine disposte alla periferia del cilindro rotante con velocità angolare costante in un campo magnetico
costante nel tempo e con distribuzione spaziale uniforme, hanno tutte lo stesso numero di spire e sono collocate in
corrispondenza dei piani diametrali e formano tra loro angoli uguali, quindi con gli assi sfasati nello spazio a 120° l’uno
dall’altro (figura 2), allora le f.e.m. generate sono sinusoidali isofrequenziali, di uguale ampiezza e si susseguono nel
senso ciclico prestabilito con uguale differenza di fase reciproca.
0°
12
Figura 2
Ciascuna tensione prende il nome di fase. E’ chiaro che le fasi si succedono, nel tempo, come indicato in figura 2,
finché il senso di rotazione del cilindro continua ad essere quello indicato. Se invece il senso di rotazione venisse
invertito, mantenendo costante il valore della velocità, anche i rapporti di fase delle singole f.e.m. indotte risulterebbero
invertiti. Quindi, una volta fissato l’ordine di successione delle fasi e quindi delle rispettive f.e.m., chiameremo senso
ciclico diretto quello per il quale le tensioni si susseguono nell’ordine prestabilito; chiameremo senso ciclico inverso,
quello per il quale l’ordine di successione risulta inverso. Usualmente si adotta come senso ciclico diretto, quello
orario.
Sistemi Trifase
Pagina 1 di 69
1.1
Sistemi simmetrici di tensioni
Un sistema come quello considerato, le cui tensioni sono sinusoidali isofrequenziali di uguale ampiezza, sfasate tra loro
di 120° in senso ciclico diretto (orario), si dice sistema trifase simmetrico di tensioni. L’espressione istantanea delle
tensioni è quindi:
=
sin
=
sin
=
sin
2
3
4
−
3
−
Nella rappresentazione simbolica, in forma esponenziale e in forma canonica, le tensioni sono espresse da:
=
=
=
=
=
=
− −
− +
√
√
"
"
√3
2
√3
2
√3
2
√3
2
Le terne simmetriche di tensioni sono, ovviamente pure, cioè godono della proprietà che la somma dei tre vettori
istantanei è nulla ad ogni istante.
I tipi fondamentali di collegamento interfasico fra le tensioni, usati nella tecnica, sono due: il collegamento a stella ed
il collegamento a triangolo (figura 3).
Esaminando i collegamenti interfasici, si rileva che le tensioni fra i morsetti di un sistema trifase possono coincidere, o
no, con le tensioni ai terminali delle fasi, a seconda del tipo di collegamento.
Chiameremo pertanto tensioni di fase $% le tensioni esistenti fra i terminali di ciascuna fase e tensioni di linea $& o
tensioni concatenate le tensioni fra due morsetti consecutivi del sistema trifase.
Figura 3
Sistemi Trifase
Pagina 2 di 69
La figura 3 mostra che nel collegamento a triangolo le tensioni di linea si identificano con le tensioni di fase; nel
collegamento a stella, invece, le tensioni di linea sono uguali alla differenza fra due consecutive tensioni di fase le
quali, in questo tipo di collegamento, coincidono ovviamente con le tensioni esistenti fra ciascuno dei morsetti delle fasi
ed il centro stella o morsetto del neutro.
Se il sistema delle tensioni è simmetrico, dalla figura 4 si deduce, con banali considerazioni geometriche, che nel
collegamento a stella le tensioni di linea hanno intensità uguale a quella delle tensioni di fase moltiplicata per √3 e sono
in anticipo di rispetto ad esse.
'
90°
30°
30°
60°
=
−
****
1) = ****
)2 =
2
+
√3
2
√3
**** = 2
+ = 2/1)
= √3
2
****
1) =
+
+
cos
= √3
6
=
'
Figura 4
Può concludersi pertanto che nei sistemi simmetrici collegati a triangolo, le tensioni di linea si identificano con le
tensioni di fase; in quelli collegati a stella, la terna delle tensioni di linea si deduce dalla terna delle tensioni di fase
ruotando solidalmente la stella dei vettori in anticipo di e moltiplicandone la lunghezza per √3.
'
E’ quasi superfluo rilevare che la terna delle tensioni di linea è sempre una terna pura (poligonale chiusa).
Sistemi Trifase
Pagina 3 di 69
1.2
Sistemi equilibrati di correnti
Applichiamo le tensioni di un sistema trifase
,
,
a tre circuiti distinti (figura 5),
Figura 5
questi vengono percorsi dalle correnti:
0 =
1̅
0 =
1̅
0 =
1̅
che risultano legate fra loro dalle relazioni costanti che dipendono, ovviamente, dalle relazioni esistenti fra le tensioni e
dai parametri degli stessi circuiti. Un sistema di correnti, come quelle che percorrono i circuiti considerati, legate tra
loro da relazioni costanti di ampiezza e di fase, si dice sistema trifase di correnti. Il complesso delle impedenze che,
alimentato da un sistema trifase di tensioni, è percorso da un sistema trifase di correnti, si dice carico trifase. I singoli
rami contenenti le impedenze si dicono fasi del carico.
Quando il sistema delle tensioni è simmetrico e le impedenze delle fasi sono uguali tra di loro (carico equilibrato), le
correnti generate hanno uguale ampiezza, uguale differenza di fase rispetto alla tensione che le genera e, di
conseguenza, uguale differenza di fase tra loro (figura 6).
1̅ = 3 + 4
0 =
56
7
8 = 0 sin9
8 = 0 sin
8 = 0 sin
− :;
−:−
−:−
Figura 6
<
"
"
0 =0
0 =0
0 =0
9=> ?;
=> ?
=> ?
"
"
Un sistema di correnti come questo, le cui correnti sono sinusoidali isofrequenziali di uguale ampiezza, sfasate tra loro
di 120° in senso ciclico diretto (orario), si dice sistema trifase equilibrato di correnti.
E’ immediato rilevare che anche per i sistemi equilibrati di correnti vale la proprietà fondamentale, già vista per i
sistemi simmetrici di tensione, in virtù della quale la somma dei valori istantanei delle correnti è nulla ad ogni istante
ed è quindi nulla anche la somma geometrica dei vettori rappresentativi di esse.
Sistemi Trifase
Pagina 4 di 69
I due tipi fondamentali di interconnessione che usualmente si adottano nella pratica, per i carichi trifase sono,
analogamente a quanto visto per le tensioni, l’interconnessione a stella e quella a triangolo (figura 7).
Esaminando i collegamenti interfasici, si rileva che le correnti che percorrono i conduttori che collegano i morsetti del
sistema generatore ai morsetti del carico trifase possono coincidere, o no, con le correnti che percorrono le singole fasi
del carico (o del sistema generatore) a seconda del tipo di interconnessione adottato.
Chiameremo pertanto correnti di fase @% le correnti che percorrono le singole fasi e correnti di linea @& quelle che
percorrono i conduttori della linea di collegamento fra il sistema generatore ed il carico (non considerando l’eventuale
conduttore di collegamento fra i neutri).
Figura 7
La figura 7 mostra che nel collegamento a stella le correnti di linea si identificano con le correnti di fase; nel
collegamento a triangolo, invece, le correnti di linea sono uguali alla differenza fra due consecutive correnti di fase.
Se il sistema delle correnti è equilibrato, dalla figura 8 si deduce, con banali considerazioni geometriche, che nel
collegamento a triangolo le correnti di linea hanno intensità uguale a quella delle correnti di fase moltiplicata per √3 e
sono in ritardo di rispetto ad esse.
'
30°
30°
90°
60°
0A = 0 − 0
****
1) = ****
)3 =
+0A +
2
√3
6
2
√3
**** = 20
+0A + = 2/1)
= √30
2
****
1) = 0 cos
0A = √30
=0
'
Figura 8
Sistemi Trifase
Pagina 5 di 69
Può concludersi pertanto che nei sistemi equilibrati, con collegamento a stella (delle fasi del carico, rispettivamente
delle fasi del generatore), le correnti di linea coincidono con le correnti di fase; con il collegamento a triangolo, il
sistema delle correnti di linea si deduce dal sistema delle correnti di fase ruotando solidalmente la stella dei vettori in
ritardo di e moltiplicandone la lunghezza per √3.
'
Anche per i sistemi equilibrati di correnti, le correnti di linea costituiscono un sistema puro ed i vettori rappresentativi
di tali correnti formano una stella regolare.
2
Sistemi simmetrici ed equilibrati
Riassumendo, si rileva che quando la regolarità della stella dei vettori rappresentativi è attribuita alle tensioni
(qualunque sia il loro collegamento interfasico) il sistema trifase si dice simmetrico; quando invece è attribuita alle
correnti, il sistema si dice equilibrato. Si dicono inoltre equilibrati quei carichi trifase che (qualunque sia la loro
interconnessione) hanno uguale impedenza in tutte le fasi.
Pertanto possiamo avere quattro tipi diversi di sistemi trifase:
Sistemi simmetrici ed equilibrati, nei quali si ha la simmetria delle tensioni e l’equilibrio nelle correnti. Essi si
realizzano alimentando un carico trifase equilibrato mediante un sistema simmetrico di tensioni.
Sistemi simmetrici e squilibrati, nei quali si ha la simmetria delle tensioni ma non l’equilibrio nelle correnti.
Essi si realizzano alimentando un carico trifase squilibrato mediante un sistema simmetrico di tensioni.
Sistemi dissimmetrici ed equilibrati, nei quali non si ha la simmetria delle tensioni ma l’equilibrio nelle
correnti. Essi si realizzano in casi molto particolari, infatti le impedenze del carico devono avere proprio quei
particolari valori per i quali le correnti prodotte da quelle determinate tensioni, si dispongono secondo una
stella regolare.
Sistemi dissimmetrici e squilibrati, nei quali non si ha né la simmetria delle tensioni né l’equilibrio nelle
correnti. Essi si realizzano alimentando un carico trifase squilibrato mediante un sistema dissimmetrico di
tensioni.
Quando mediante un sistema trifase di tensioni, si alimenta un carico trifase, il regime elettrico che si stabilisce nel
sistema è diverso a seconda del collegamento interfasico adottato per il sistema generatore e del tipo di interconnessione
adottata per il carico. Le varie combinazioni che possono verificarsi sono quattro:
1)
2)
3)
4)
Collegamento
interfasico delle
tensioni
Interconnessione
del carico
Stella
Stella
Triangolo
Triangolo
Stella
Triangolo
Stella
Triangolo
Conviene comunque, ai fini del calcolo del circuito, ricondurre ognuna delle quattro combinazioni alla prima o
all’ultima di esse.
Per i sistemi simmetrici ed equilibrati, il calcolo è particolarmente agevole per la combinazione stella-stella, che si
assume perciò come sistema tipico di tali sistemi.
Sistemi Trifase
Pagina 6 di 69
Consideriamo tre circuiti monofase indipendenti (figura 9a), aventi uguale impedenza 1̅, alimentati da tre generatori le
cui tensioni , , , costituiscono un sistema trifase simmetrico e che pertanto generano nei circuiti tre correnti
0 , 0 , 0 , costituenti un sistema equilibrato.
Figura 9
Se tutti i conduttori di ritorno sono ora riuniti fra loro in uno stesso conduttore (figura 9b), si ottiene un sistema trifase
stella-stella, nel quale i morsetti delle fasi del generatore risultano collegati, mediante tre conduttori di linea, ai morsetti
delle fasi del carico ed il neutro del generatore risulta collegato al centro stella del carico mediante un quarto conduttore
che chiameremo conduttore neutro. Nel neutro vengono quindi convogliate tutte le correnti del sistema trifase; poiché
esse costituiscono un sistema equilibrato e, di conseguenza, la loro somma è in ogni istante nulla, il conduttore neutro
risulta percorso da una corrente identicamente nulla e può quindi essere soppresso senza che niente muti nel regime
elettrico del sistema. Si rileva quindi che la d.d.p. fra il punto neutro del sistema generatore ed il centro stella del carico
è anch’essa identicamente nulla.
Quest’ultima affermazione può anche essere constatata applicando Millmann tra On ed Os:
BC BD
1
̅ + 1̅ + 1̅
̅F
1
1
=E =
=
1 1 1
+ +
1̅ 1̅ 1̅
+
3
1̅
+
G
Ed essendo la terna delle tensioni una terna simmetrica e quindi pura, si ottiene:
BC BD
1
̅ + 1̅ + 1̅
̅F
1
1
=E =
=
1 1 1
+ +
1̅ 1̅ 1̅
+
3
1̅
+
G
=0
Quando il sistema è simmetrico ed equilibrato, i tre circuiti monofase indipendenti che nel loro complesso sono
equivalenti al sistema trifase, sono tutti uguali tra loro; quindi lo studio del regime del sistema trifase può ricondursi a
quello di uno solo di essi. Pertanto il calcolo di un sistema trifase simmetrico ed equilibrato può essere effettuato
limitandoci ad eseguire il calcolo di un circuito monofase (figura 9c) così costituito:
dalla tensione I di una fase del generatore;
dall’impedenza 1̅ di una fase del carico;
da un conduttore della linea e dal conduttore neutro.
Applicando tale principio, ogni corrente 0I del sistema trifase può dedursi immediatamente dalla rispettiva tensione
dividendola per l’impedenza.
Sistemi Trifase
Pagina 7 di 69
Per esempio abbiamo:
0 =
1̅
=
1
?
=
?
1
=0
?
E poiché il sistema è equilibrato, otteniamo le altre correnti ruotando in ritardo 0 di 120° ed ancora di ulteriori 120°
0 =0
0 =0
0 =0
?
<
"
"
Il calcolo dei sistemi simmetrici ed equilibrati con collegamento interfasico a triangolo del sistema generatore, può
essere ricondotto a quello con collegamento a stella, introducendo il concetto di tensioni stellate.
Dati i tre conduttori di linea di un sistema trifase e le relative tensioni concatenate
,
,
, chiameremo baricentro
elettrico del sistema, il punto Ob ottenuto unendo a stella tre impedenze uguali collegate ai conduttori di linea (figura
10).
Figura 10
La definizione del baricentro elettrico, essendo riferita unicamente ai conduttori di linea, prescinde completamente dal
collegamento interfasico del generatore. E’ evidente inoltre che in ogni sistema simmetrico ed equilibrato il baricentro
Ob corrisponde al punto neutro On del generatore (nel senso che la d.d.p. fra i due è identicamente nulla) quando questo
è connesso a stella e corrisponde altresì al centro stella di ogni carico equilibrato a stella connesso alla linea stessa.
Chiameremo poi tensioni stellate baricentriche J , J , J le tre tensioni esistenti fra ciascun conduttore di linea ed il
baricentro. E’ superfluo notare anche che il baricentro elettrico del sistema coincide con il baricentro geometrico del
triangolo i cui lati sono i vettori concatenati (tensioni di linea) della terna simmetrica di tensioni. Da quanto già detto, è
chiaro che:
J
=
J
=
J
=
1
√3
1
√3
1
√3
'
'
'
La figura 11 riassume sinteticamente il calcolo di un sistema trifase simmetrico ed equilibrato in tutti i casi possibili.
Sistemi Trifase
Pagina 8 di 69
Figura 11
Sistemi Trifase
Pagina 9 di 69
2.1
Potenza nei sistemi simmetrici ed equilibrati
Dato un sistema trifase simmetrico ed equilibrato, con collegamento stella-stella, le espressioni istantanee delle tensioni
di fase e delle correnti di fase sono:
=
=
=
sin
sin
−
sin
−
<
8 = 0 sin9
"
8 = 0 sin
"
8 = 0 sin
− :;
−:−
−:−
Le potenze istantanee erogate da ciascun generatore sono:
K =
8 =
K =
=
K =
QR ST UV
=
N
8
3
sin
<
"
"
0 sin9 − :; = 0Lcos : − cos92 − :;M = 0 cos : − 0 cos92
2
2
8 =
sin
−
0 sin
−:−
=
3
3
4
4
0 Ncos : − cos 2 − : −
O = 0 cos : − 0 cos 2 − : −
3
3
4
4
8 =
sin
−
0 sin
−:−
=
3
3
8
8
0 Ncos : − cos 2 − : −
O = 0 cos : − 0 cos 2 − : −
3
3
= 2 +
2
3
=
− :;
2
O
3
Sommando quindi membro a membro le precedenti equazioni, otteniamo la potenza istantanea per il sistema trifase
simmetrico ed equilibrato:
K=K +K +K =
0 cos : − 0 cos92
0 cos : − 0 cos 2
0 cos : − 0 cos 2
− :; +
4
−:−
3
8
−:−
3
+
Essendo le tre potenze fluttuanti tre sinusoidi di uguale ampiezza e sfasate tra loro di 120°, si ha che la loro somma è
uguale a zero, di conseguenza:
K = 3 0 cos :
Ricordando che V e I sono i valori efficaci delle grandezze di fase (collegamento stella-stella), possiamo scrivere:
K = 3 W 0W cos :
Per questo possiamo affermare che in un sistema trifase simmetrico ed equilibrato la potenza istantanea è costante ed è
uguale al triplo del prodotto dei valori efficaci della tensione di fase W e della corrente di fase 0W , moltiplicato per il
coseno dell’angolo di fase : tra W e 0W (angolo caratteristico delle impedenze del carico).
Questo vuol dire anche che la potenza fluttuante complessiva è nulla (attenzione che la potenza fluttuante in ogni fase
non è nulla), quindi rilevare che in un sistema trifase la potenza fluttuante complessiva è nulla garantisce che il sistema
sia simmetrico ed equilibrato.
Rammentando ora che la potenza attiva è definita come il valor medio della potenza istantanea, possiamo affermare che
la potenza attiva trifase è:
X = 3 W 0W cos :
Che, ovviamente, coincide con la somma delle potenze attive messe in gioco da ciascuna fase.
Analogamente la potenza reattiva trifase è la somma delle potenze reattive messe in gioco da ciascuna fase, per cui:
Y = 3 W 0W sin :
Sistemi Trifase
Pagina 10 di 69
Occorre puntualizzare che nei sistemi trifase, la potenza reattiva perde il significato fisico di ampiezza della potenza
reattiva istantanea ed assume solo un significato puramente matematico.
Usualmente, però, la potenza di un sistema trifase viene espressa in termini di grandezze di linea e quindi, tenendo
presente che:
0Z = 0W
0Z = √30W
nel collegamento a stella
nel collegamento a triangolo
si ottiene:
Z
Z
collegamento a stella
W
collegamento a triangolo
X = 3 W 0W cos : = 3
Y = 3 W 0W sin : =
= √3
= W
5[
0 cos : = √3 Z 0Z cos :
√ Z
5[
3 0Z sin : = √3 Z 0Z sin :
√
X = 3 W 0W cos : = 3
Y = 3 W 0W sin : = 3
In definitiva definiamo potenza attiva trifase
\[
Z √ cos : = √3 Z 0Z cos :
\[
Z √ 0Z sin : = √3 Z 0Z sin :
X = √3 Z 0Z cos :
e potenza reattiva trifase
Y = √3 Z 0Z sin :
E’ importante evidenziare che le due formule precedenti sono formule “ibride” poiché contengono sia grandezza di
linea ( Z , 0Z ), sia grandezze di fase (:); infatti : è lo sfasamento tra il vettore tensione di fase ed il vettore corrente di
fase.
Definiamo poi potenza apparente trifase:
] = ^X + Y = √3 Z 0Z
Inoltre, utilizzando il teorema di Boucherot, definiamo potenza complessa di un sistema trifase simmetrico ed
equilibrato:
]̅ = 3 W /0_W = ]
?
Il fattore di potenza, definito come rapporto tra potenza attiva e potenza apparente, nel sistema trifase simmetrico ed
equilibrato sarà:
`. b. K. =
X √3 Z 0Z cos :
=
= cos :
]
√3 Z 0Z
Possiamo quindi affermare che nei sistemi trifase simmetrici ed equilibrati il fattore di potenza coincide, come per i
sistemi monofase, con il coseno dell’angolo caratteristico delle impedenze del carico.
Comunque è bene fin d’ora definire il fattore di potenza di un sistema trifase come il coseno dell’angolo di cui va
ruotata la stella dei vettori delle correnti, rispetto a quella delle tensioni, affinché l’espressione della potenza attiva del
sistema assuma il massimo valore possibile.
Sistemi Trifase
Pagina 11 di 69
2.2
Misura della potenza nei sistemi simmetrici ed equilibrati
Lo schema di principio per la misura delle potenze in un sistema trifase, discende immediatamente dalle loro
definizioni:
X = X +X +X
Y = Y +Y +Y
per cui le potenze trifase si possono misurare facendo la somma delle potenza misurate in ciascuna delle fasi.
Nel caso di sistemi trifase simmetrici ed equilibrati è sufficiente la misura delle potenze di una sola fase per dedurre,
moltiplicando per tre, le potenze trifase:
X = 3 W 0W cos :
Y = 3 W 0W sin :
Se però la misura deve essere eseguita in base alle sole grandezze di linea prescindendo dal generatore e dal carico, si
costruisce, con tre impedenze uguali, un baricentro Ob del sistema e si inserisce un wattmetro in modo che la bobina
amperometrica sia percorsa dalla corrente di uno dei conduttori della linea e che alla bobina voltmetrica sia applicata la
tensione baricentrica tra lo stesso conduttore ed il baricentro Ob.
E’ facile vedere (figura 12) che, qualunque sia il collegamento interfasico dei generatori, l’indicazione del wattmetro è:
e che, quindi, la potenza attiva trifase è data da:
c=
W 0W
cos :
X = 3c
Per determinare poi la potenza reattiva trifase, basta misurare la tensione e la corrente di linea, con voltmetro e
amperometro, ricavare la potenza apparente:
e dedurre Q come:
Sistemi Trifase
] = √3 Z 0Z
Y = ^] − X
Pagina 12 di 69
W=Vb I l cos (Vb I l)
Il
Il
Vl
Carico a stella
J
=
0Z = 0W
Carico a triangolo
W
J
=
0Z = 0W
c=
d
e
d
e
perciò
W
J
f =
J 0Z cos J 0Z
In definitiva
=
√
W
0Z = √30W
f0 = f0 = :
J Z
W W
quindi
√
W
0Z = √30W
perciò
J
=
f0 = f0 = :
J Z
W W
W 0W
cos : =
quindi
g
X = 3c
c=
] = √3 Z 0Z
f =
J 0Z cos J 0Z
√
W √30W
cos : =
W 0W
cos : =
g
Y = √] − X
Figura 12 - Metodo del wattmetro inserito tra una fase ed il baricentro
(applicabile solo ai sistemi simmetrici ed equilibrati)
Sistemi Trifase
Pagina 13 di 69
Molto più usato è il ricorso a due wattmetri inseriti secondo l’inserzione Aron (questo perché dalle indicazioni dei due
wattmetri è possibile risalire pure alla potenza reattiva). I due wattmetri sono inseriti su due fasi qualsiasi e gli
equipaggi voltmetrici sono collegati tra la fase sulla quale il wattmetro è inserito e la fase rimasta libera (nella figura si
sono utilizzate le fasi 1 e 2, ma si potrebbero usare anche le fasi 1 e 3 oppure 2 e 3). Dei due wattmetri, quello inserito
sulla fase che si trova a essere immediatamente in anticipo (secondo la sequenza ...-1-2-3-1-2-3-1-... ) viene chiamato
primo wattmetro (o wattmetro in ponte maggiore) mentre l'altro viene chiamato secondo wattmetro (o wattmetro in
ponte minore), nel nostro esempio il primo wattmetro è il WA mentre in secondo è il WB.
Figura 13 - Inserzione Aron
L'indicazione dei due wattmetri, per un sistema simmetrico nelle tensioni ed equilibrato nel carico, vale:
ch = V
cm = V
∙ 0Z = VZ 0Z URk l
∙ 0Z = VZ 0Z cos n
essendo l e n gli sfasamenti fra i vettori rappresentativi delle tensioni e delle correnti che interessano le bobine dei due
wattmetri e rispettivamente pari a l = : − , n = : + , come si può dedurre osservando il diagramma vettoriale
'
'
riportato sotto e facente riferimento al caso di un carico ohmico-induttivo (correnti di linea in ritardo dell'angolo :
rispetto alle corrispondenti tensioni stellate).
Dalla figura 13 e dal diagramma vettoriale si deduce che:
ch =
cm =
Sistemi Trifase
1
√3
cos : + VZ 0Z sin :
2
2
1
√3
∙ 0 = Z 0Z cos n = VZ 0Z cos : + " = VZ 0Z cos : cos − sin : sin " = VZ 0Z
cos : − VZ 0Z sin :
6
6
6
2
2
∙ 0 = VZ 0Z cos l = VZ 0Z cos : − " = VZ 0Z cos : cos + sin : sin " = VZ 0Z
6
6
6
Pagina 14 di 69
Sommando e sottraendo membro a membro le precedenti equazioni, si ottiene:
ch + cm = VZ 0Z
1
1
√3
√3
cos : + VZ 0Z sin : + VZ 0Z
cos : − VZ 0Z sin : = √3VZ 0Z cos : = X
2
2
2
2
ch − cm = VZ 0Z
Y
1
1
√3
√3
cos : + VZ 0Z sin : − VZ 0Z
cos : + VZ 0Z sin : = VZ 0Z sin : =
2
2
2
2
√3
Cioè, la somma delle indicazioni dei wattmetri, inseriti in Aron, è uguale alla potenza attiva trifase che fluisce nella
linea, la loro differenza, moltiplicata per √3, è uguale alla potenza reattiva trifase.
X = ch + cm
Y = √39ch − cJ ;
Se invece dei wattmetri inserissimo due varmetri, sempre in Aron, avremmo:
o3h =
o3m =
1
√3
sin : − Z 0Z cos :
2
2
1
√3
⋀0 = Z 0Z cos n = Z 0Z sin : + " = Z 0Z sin : cos + cos : sin " = Z 0Z
sin : + Z 0Z cos :
2
6
6
6
2
⋀0 = Z 0Z k8Q l = Z 0Z sin : − " = Z 0Z sin : cos − cos : sin " = Z 0Z
o3h =
o3m =
⋀0Z = VZ 0Z sin l
⋀0Z = VZ 0Z sin n
6
√3
sin : −
2
√3
o3h − o3m = Z 0Z
sin : −
2
o3h + o3m =
Z 0Z
1
cos : +
2
1
Z 0Z cos : −
2
Z 0Z
6
√3
sin : +
2
√3
sin : −
Z 0Z
2
Z 0Z
6
1
cos : = √3 Z 0Z sin : = Y
2
1
X
Z 0Z cos : = − Z 0Z cos : = −
2
√3
Z 0Z
Cioè, la somma delle indicazioni dei varmetri, inseriti in Aron, è uguale alla potenza reattiva trifase che fluisce nella
linea, la loro differenza, moltiplicata per √3 e cambiata di segno, è uguale alla potenza attiva trifase.
Y = o3h + o3m
X = −√39 o3h − o3J ;
E’ possibile, chiaramente solo ai fini del calcolo, calcolare la potenza complessa trifase immaginando di inserire in
Aron due “vacmetri”, strumenti questi che chiaramente sono inventati, per cui
e, infine:
Sistemi Trifase
]h̅ =
]m̅ =
∙ 0_
∙ 0_
]̅ = ]h̅ + ]m̅
Pagina 15 di 69
2.3
Campo magnetico rotante di Galileo Ferraris
Galileo Ferraris scoprì e dimostrò un’importante proprietà dei sistemi trifase e cioè che questi sistemi possono generare
dei campi magnetici rotanti mediante sistemi trifase di correnti che percorrono avvolgimenti fissi nello spazio.
Immaginiamo di disporre tre bobine identiche, cioè di uguale materiale, uguale lunghezza ed ugual numero di spire N,
in una posizione fissa nello spazio, nella quale i loro assi siano complanari e formino tra di loro angoli di 120° l’uno
rispetto all’altro (figura 14) e supponiamo di alimentarle con una terna simmetrica di tensioni. Essendo quindi le bobine
un carico equilibrato, le stesse saranno percorse da un terna equilibrata di correnti.
H
H
H
Figura 14
Se il mezzo è isotropo e la sua permeabilità magnetica è costante, le bobine generano tre campi magnetici che, nella
zona centrale di esse, hanno una direzione coincidente con quella dell’asse delle rispettive bobine ed una intensità
variabile nel tempo con la medesima legge sinusoidale delle correnti che li producono:
q 9 ; = q sin
2
3
4
−
3
q 9 ; = q sin
−
q 9 ; = q sin
rstuv 9 ; è ovviamente, istante per istante, la somma geometrica dei tre vettori q
rs 9 ;, q
rs 9 ;, q
rs 9 ;:
Il campo risultante q
rstuv 9 ; = q
rs 9 ; + q
rs 9 ; + q
rs 9 ;
q
Riferendoci al piano di Gauss coincidente con il piano degli assi delle bobine (figura 15) abbiamo:
H
H
√
√
H
H
H
H
Figura 15
Sistemi Trifase
Pagina 16 di 69
rstuv 9 ; =
q
Ed essendo:
q 9 ; = q sin
q 9 ; = q sin
q 9 ; = sin
Avremo:
Per cui:
−
−
4
3
2
3
rs 9 ; = − q 9 ; = − q sin
q
1
√3
rs 9 ; = −
q 9 ;+ q 9 ;
q
2
2
1
√3
rs 9 ; = +
q
q 9 ;+ q 9 ;
2
2
q 9 ;+q 9 ;
√3
Lq 9 ; − q 9 ;M + w
− q 9 ;x
2
2
= q Nsin
= q Nsin
1
q 9 ; − q 9 ; = q y− sin
2
1
q 9 ; + q 9 ; = q y− sin
2
cos −
cos −
+
4
3
√3
cos
2
+
2
3
√3
cos
2
− cos
− cos
sin −
sin −
4
3
1
z − q y− sin
2
1
z + q y− sin
2
2
3
1
O = q y− sin
2
1
O = q y− sin
2
−
√3
cos
2
−
√3
cos
2
q 9 ;+q 9 ;
√3
Lq 9 ; − q 9 ;M + w
− q 9 ;x
2
2
1
3
√3
=
+ − q sin
− q sin
= q cos
√3q cos
2
2
2
rstuv 9 ; =
q
−
+
−
√3
cos
2
√3
cos
2
z
z
z = √3q cos
z = −q sin
3
q sin
2
=
3
q
2
=>
rstuv 9 ; ha un’intensità costante nel tempo pari ad una volta e
In definitiva abbiamo ottenuto che il campo risultante q
mezzo il campo massimo q prodotto da ciascuna bobina ed una direzione che ruota nello spazio, rispetto al sistema
che lo genera, a velocità costante , pari alla pulsazione delle correnti; quindi questo campo compie un giro completo
ogni ciclo della corrente. Il senso di rotazione del campo è concorde al senso ciclico delle correnti che lo generano.
Sistemi Trifase
Pagina 17 di 69
Allo stesso Galileo Ferraris è dovuto il principio dell’equivalenza fra un campo alternativo ed un complesso di due
campi rotanti in senso opposto l’uno con l’altro.
Consideriamo un campo alternativo avente direzione fissa nello spazio (figura 16) ed una intensità variabile nel tempo
con legge sinusoidale:
q{Z> 9 ; = q sin
H
H
H
H
H
Figura 16
Consideriamo poi due campi magnetici di intensità costante nel tempo, pari ad q , e direzione rotante nello spazio a
velocità angolare costante, uguale alla pulsazione ; i sensi di rotazione dei due campi siano fra loro opposti e
rs| 9 ; il campo che ruota in senso orario e componente inverso q
rsu 9 ; quello che ruota in
chiamiamo componente diretto q
senso opposto.
rsu 9 ; all’istante zero hanno direzione perpendicolare alla direzione di q{Z> e senso l’uno opposto all’altro,
rs| 9 ; ed q
Se q
è chiaro che ad ogni istante la loro posizione è sempre simmetrica rispetto alla direzione del campo alternativo e, quindi,
la loro risultante ha sempre la stessa direzione di tale campo ed una intensità identicamente uguale all’intensità di esso:
rstuv 9 ; = q
rs| + q
rsu = 2
q
rs
q
sin
2
rs{Z> 9 ;
=q
Possiamo quindi concludere che un campo alternativo è equivalente a due campi rotanti in senso opposto, con velocità
angolare uguale alla pulsazione del campo alternativo ed aventi una intensità costante uguale alla metà del valore
massimo del campo alternativo stesso.
Sistemi Trifase
Pagina 18 di 69
3
Sistemi dissimmetrici e squilibrati
Un sistema trifase dissimmetrico e squilibrato è un sistema che tramite tre tensioni che hanno in comune solo la
frequenza alimenta un carico costituito da tre impedenze diverse tra loro (figura 17).
=
=
=
sin9
sin9
sin9
+} +: ;
+} +: ;
+} +: ;
Figura 17
Molte reti di distribuzione in BT hanno una configurazione formata da un sistema generatore connesso a stella (figura
18a), il quale alimenta i vari carichi mediante una linea di collegamento costituita da quattro conduttori, tre partono dai
morsetti delle fasi ed il quarto dal centro stella (morsetto del neutro). Questa configurazione caratterizza il sistema che
chiameremo sistema trifase a quattro fili.
0Z + 0Z + 0Z + 0~ = 0
a)
0Z + 0Z + 0Z = 0
Sistema a quattro fili
0Z + 0Z + 0Z =
= F0W − 0W G + F0W − 0W G + F0W − 0W G = 0
b) Sistema a tre fili
Figura 18
Sistemi Trifase
Pagina 19 di 69
A differenza delle reti di distribuzione prima citate, le grandi condutture trifase per il trasporto dell’energia sono
usualmente costituite dai soli conduttori che hanno origine dai tre morsetti delle fasi. La loro configurazione, quindi, è
quella di un sistema con generatore connesso a triangolo, oppure a stella, ma il morsetto del neutro non ha collegamento
con le utenze (figura 18b). Il sistema avente tale configurazione è detto sistema trifase a tre fili.
Nei sistemi a tre fili, come si rileva dalla figura, la somma delle correnti di linea è sempre nulla; e poiché abbiamo già
visto che anche la somma delle tre tensioni di linea è in ogni caso identicamente uguale a zero, concludiamo che nei
sistemi trifase dissimmetrici e squilibrati a tre fili, le terne delle grandezze di linea sono sempre pure.
3.1
Tensioni e correnti nei sistemi trifase a tre fili
Nei sistemi trifase dissimmetrici e squilibrati, il tipo di carico per il quale il calcolo delle grandezze si esegue con
maggiore facilità, è quello con le fasi del carico connesse a triangolo (figura 19).
0W =
0Z + 0Z + 0Z = 0
+
+
=0
0W =
0W =
Infatti, note le tensioni concatenate della linea
carico.
,
0W =
0W =
0W =
0Z = 0W − 0W =
5•
7*•
0Z = 0W − 0W =
5
7*
0Z = 0W − 0W =
5•
7*
5•
7*•
5
7*
5•
7*
−
−
−
5•
7*
5•
7*•
5
7*
Figura 19
,
1̅
1̅
1̅
, si calcolano immediatamente le correnti nelle fasi del
=
=
=
1
?•
1
?
?
1
dove : , : , : sono gli angoli caratteristici delle impedenze del carico. Sottraendo poi a due a due queste correnti, si
ottengono le correnti di linea:
0Z = 0W − 0W =
0Z = 0W − 0W =
0Z = 0W − 0W =
Sistemi Trifase
1̅
1̅
1̅
−
−
−
1̅
1̅
1̅
Pagina 20 di 69
Se invece il carico è connesso a stella, il calcolo oltre che con i metodi classici (per esempio Millmann e Kirchhoff) si
può ricondurre al caso precedente sostituendo alla stella del carico, il triangolo equivalente tramite le note formule
(figura 20).
1̅
1̅
1̅
1̅ 1̅
1€̅
1̅ 1̅
=
1€̅
1̅ 1̅
=
1€̅
=
1̅ 1̅
1v̅
1̅ 1̅
1̅ =
1v̅
1̅ 1̅
1̅ =
1v̅
1̅ =
1€̅ =
1
1
1
1
+ ̅ + ̅
̅
1
1
1
1v̅ = 1̅
+ 1̅
91;
+ 1̅
92;
Figura 20
Fatta quindi l’equivalenza stella triangolo, si calcolano le correnti di fase del triangolo:
0
=
0
=
0
=
1̅
1̅
1̅
E facendo la differenza a due a due fra queste correnti, si ricavano le correnti di linea che, poi, altro non sono che le
correnti di fase dell’originario carico a stella:
0Z = 0W = 0
−0
=
0Z = 0W = 0
−0
=
0Z = 0W = 0
Sistemi Trifase
−0
=
1̅
1̅
1̅
−
−
−
1̅
1̅
1̅
Pagina 21 di 69
3.2
I centri stella nei sistemi trifase dissimmetrici e squilibrati
Data una linea trifase ed il relativo sistema di tensioni concatenate
,
,
, chiameremo genericamente centro
stella •‚ , il punto di connessione di una qualunque stella di tre impedenze 1̅ , 1̅ , 1̅ , scelte arbitrariamente e collegate
ai conduttori di linea (figura 21).
Figura 21
E’ chiaro che per un determinato sistema trifase di tensioni concatenate possono costruirsi infiniti centri stella variando
ad arbitrio le impedenze della stella. Quando le tre impedenze 1̅ , 1̅ 1̅ sono uguali fra loro, il relativo centro stella,
come già visto, si dice baricentro elettrico 9•ƒ ; del sistema trifase.
Chiameremo poi terna di tensioni stellate F$„‚ , $…‚ , $†‚ G, rispetto ad un determinato centro stella 9Oˆ ;, le tensioni fra
ciascun conduttore di linea ed ‰v . Quando il centro stella prescelto è il baricentro del sistema, le tensioni stellate, come
già detto, si dicono baricentriche F J , J , J G.
E’ facile rilevare che ogni tensione di linea o concatenata, risulta uguale alla differenza fra due successive tensioni
stellate di ogni terna. Pertanto, qualunque sia il centro stella prescelto, le tensioni stellate sono legate alle tensioni
concatenate dalle relazioni:
=
=
=
−
v−
v−
v
v
v
v
Tutte le terne di tensioni stellate derivate da una stessa linea, se questa è prevalente, hanno in comune fra loro la stessa
terna di tensioni concatenate
,
,
. Perciò le differenze omologhe fra due consecutive tensioni stellate, essendo
uguali alla stessa tensione di linea, sono uguali in tutte le terne:
=
=
=
Sistemi Trifase
−
vŠ −
vŠ
vŠ −
v‹
v‹
v‹
=
=
=
−
v" −
v"
v" −
v"
v"
v"
=⋯
=⋯
=⋯
Pagina 22 di 69
Quindi se nella rappresentazione polare delle tensioni (figura 22) si disegna innanzitutto il triangolo delle tre tensioni di
linea F ,
,
G e si riportano poi nel diagramma i vettori delle varie terne stellate con l’origine in altrettanti diversi
poli, in modo che gli estremi dei vettori v , v
v coincidano in ogni caso con i corrispondenti vertici del triangolo
disegnato, tutte le terne di tensioni stellate derivate dalla linea risultano rappresentate da stelle di vettori a vertici
comuni.
Figura 22
E’ chiaro allora che i poli delle varie terne corrispondono ai relativi centri stella e che la tensione fra due qualsiasi centri
stella del sistema è rappresentata dal vettore congiungente i due poli corrispondenti.
Tra le infinite terne di tensioni stellate relative ad un determinato sistema trifase, si distingue, per alcune importanti
proprietà caratteristiche, la terna delle tensioni baricentriche.
Consideriamo il baricentro OŽ ottenuto derivando dalla linea tre impedenze uguali 1̅ (figura 23). Indicando con
0 J , 0 J , 0 J , le correnti che percorrono tali impedenze (la loro somma per l’equazione al nodo OŽ è nulla), si ha:
J
+
J
+
J
= 1̅F0
J
+0
J
+ 0 JG = 0
Figura 23
Sistemi Trifase
Pagina 23 di 69
Vale a dire che la terna delle tensioni baricentriche è sempre pura. E’ evidente inoltre che il punto OŽ coincide con il
baricentro geometrico del triangolo i cui lati rappresentano le tensioni di linea.
La differenza di potenziale esistente tra il baricentro OŽ del sistema ed un qualunque centro stella Oˆ è rappresentata nel
diagramma polare della figura 23 dal vettore Jv che unisce Oˆ con OŽ . L’espressione simbolica si deduce dalle
relazioni:
+
Jv +
Jv +
Jv
J
J
J
=
=
=
v
v
v
Infatti, sommandole membro a membro e ricordando che la terna baricentrica è pura, si ottiene:
Jv
=
v
+
v
3
+
v
Vale a dire, la tensione Jv fra il baricentro del sistema ed un centro stella generico ‰v è espressa, in termini simbolici,
dalla media aritmetica delle tre tensioni stellate rispetto ad ‰v .
Questa tensione può, evidentemente, essere espressa anche in funzione delle tensioni baricentriche e delle ammettenze
del carico, applicando Millmann si ottiene:
Jv
* + J •* +
•* + •* + •*
*
J•
=−
J•
o può ottenersi anche scrivendo l’equazione al nodo ‰v (figura 23):
0 v+ 0 v+0
Essendo:
0
0
0
Si ha
F
* +
v•
Jv
Sistemi Trifase
* +
J•
Jv
+
=−
* +
v•
* +F
J G•
v
v
v
Jv
+
v•
*
=
v•
*
=
* + J •* +
*
*
J• +
J• +
•* + •* + •*
J•
=0
*
=
v•
* =0
v•
v
* +F
J G•
Jv
+
* =0
J G•
* + •* + •* ; = 0
*
J•
Jv 9•
Pagina 24 di 69
La formula:
Jv
=
v
+
v
3
+
v
consente di stabilire delle semplici relazioni tramite le quali si possono esprimere le tensioni stellate baricentriche in
funzione delle tensioni di linea. Supponiamo, essendo il centro stella Oˆ arbitrario, di far coincidere Oˆ con il vertice 1
del triangolo di figura 23. Le tensioni stellate rispetto a tale centro stella saranno:
9 ;
v
=0
9 ;
v
=
9 ;
v
sostituendo otteniamo
e poiché
9 ;
Jv
9 ;
Jv
=
9 ;
v
+
9 ;
v
3
=−
+
9 ;
v
=
−
non è altro che l’opposto della tensione stellata baricentrica
9 ;
Jv
=
−
+
3
ed infine
J
=
J
=
=−
+
3
J,
si ha:
J
−
3
Banalmente, con analogo procedimento, è cioè facendo coincidere Oˆ con i vertici 2 e 3 del triangolo delle tensioni di
linea, otteniamo:
J
Sistemi Trifase
=
−
3
−
3
Pagina 25 di 69
3.3
Potenza nei sistemi dissimmetrici e squilibrati
Dato un sistema trifase dissimmetrico e squilibrato, a tre o quattro fili, l’andamento degli scambi energetici, può
rilevarsi dall’esame della variazione nel tempo delle potenze istantanee, K , K , K , erogate dai tre generatori (o
assorbite dalle tre fasi del carico). La potenza trifase istantanea che il sistema trasmette alla linea (o che il carico
assorbe dalla linea), è data dalla somma delle tre potenze istantanee.
Date quindi le correnti e le tensioni relative alle singole fasi:
=
=
=
Abbiamo:
sin9
sin9
sin9
8 =0
8 =0
8 =0
+} +: ;
+} +: ;
+} +: ;
K = K +K +K =
=
+
+
8
0
0
0
+ 8
cos :
cos :
cos :
+
−
−
−
8
0
0
0
sin9
sin9
sin9
=
cos92
cos92
cos92
+} ;
+} ;
+} ;
+ 2} + • ; +
+ 2} + • ; +
+ 2} + • ;
La potenza istantanea è quindi, come ben noto, costituita da due addendi, il primo costante (Potenza Costante):
K‘ =
0 cos : +
ed il secondo variabile (Potenza Fluttuante):
KWZ = −L 0 cos92
=
0 sin 2
+ 0 sin 2
+ 0 sin 2
+ 2} + • ; +
+ 2} + • − " +
2
+ 2} + • − " +
2
0 cos : +
0 cos92
0 cos :
+ 2} + • ; +
0 cos92
+ 2} + • ;M =
+ 2} + • − "
2
La potenza fluttuante è quindi costituita dalla somma delle potenze fluttuanti messe in gioco da ciascuna fase.
Diversamente da quanto avviene nei sistemi trifase simmetrici ed equilibrati, dove abbiamo visto che la potenza
fluttuante trifase è nulla, in questi sistemi la stessa è presente e costituisce un peculiare carattere distintivo del regime
dissimmetrico e squilibrato.
Generalizzando ora le definizione già note, diremo Potenza Attiva Trifase P e Potenza Reattiva Trifase Q di un sistema
dissimmetrico e squilibrato la somma delle potenze attive e delle potenze reattive delle tre fasi:
X = X + X + X = 0 cos : + 0 cos : +
Y = Y + Y + Y = 0 sin : + 0 sin : +
0 cos :
0 sin :
La potenza attiva trifase, come noto, è sempre il valor medio della potenza istantanea, mentre in questi sistemi la
potenza reattiva trifase non ha alcun significato fisico.
Definiamo poi, come per gli altri sistemi, Potenza Apparente Trifase S e Potenza Complessa Trifase “
’,
rispettivamente:
] = ^X + Y
]̅ = ]̅ + ]̅ + ]̅ =
Sistemi Trifase
∙ 0_ +
∙ 0_ +
∙ 0_ =
0
?•
+
0
?
+
0
?
=X + Y +X + Y +X + Y
Pagina 26 di 69
Nei sistemi trifase dissimmetrici e squilibrati non è più possibile definire il fattore di potenza in funzione degli angoli
caratteristici del carico. Utilizzando quindi la definizione generale, abbiamo:
`. b. K. =
X
]
Se vogliamo comunque utilizzare, per comodità, un coseno, possiamo affermare che il fattore di potenza coincide con il
coseno dell’angolo di cui va ruotata la stella delle correnti rispetto a quella delle tensioni o viceversa affinché
l’espressione della potenza attiva risulti massima.
3.4
Teorema di Aron
Consideriamo un sistema a tre fili dissimmetrico e squilibrato e costruiamo un qualsiasi centro stella Os (figura 24);
Figura 24 – Teorema di Aron
Sistemi Trifase
Pagina 27 di 69
Si rileva che l’espressione (potenza attiva, rispetto ad Os):
X9‰v ; =
v 0Z
cos : v +
v 0Z
cos :
v
+
v 0Z
cos :
v
=
v
∙ 0Z +
v
∙ 0Z +
v
∙ 0Z
è invariante rispetto al centro stella, non varia cioè di valore qualsiasi sia il centro stella scelto.
Supponiamo di costruire ora un altro centro stella qualsiasi Os’ ed indichiamo con vvŠ la tensione tra i due centri stella,
avremo:
X9‰vŠ ; =
=
∙ 0Z + vŠ ∙ 0Z +
∙
vvŠ F0Z + 0Z + 0Z G +
∙ 0Z = F
v ∙ 0Z +
vŠ
vŠ
+ v G ∙ 0Z + F
∙
v 0Z +
v ∙ 0Z
vvŠ
vvŠ
+
vG
∙ 0Z + F
vvŠ
+
vG
∙ 0Z
Ed essendo la terna delle correnti una terna pura, cioè la somma delle correnti è zero, si ha:
X9‰vŠ ; =
v
∙ 0Z +
v
∙ 0Z +
v
∙ 0Z = X9‰v ;
L’invarianza vale anche, ovviamente, per i centri stella •” od •• dei generatori o del carico (se connessi a stella);
perciò indicando con P la potenza attiva trifase del sistema, si ha:
X9‰vŠ ; =
v
∙ 0Z +
v
∙ 0Z +
v
∙ 0Z = X
Quindi possiamo terminare affermando che la potenza attiva trifase di un sistema trifase a tre fili qualsiasi è uguale
alla somma dei prodotti scalari delle correnti di linea per le corrispondenti tensioni stellate relative ad un qualunque
centro stella scelto ad arbitrio (Teorema di Aron).
Il teorema, dimostrato nel caso di generatori o carichi supposti a stella, è valido anche nel caso in cui siano connessi a
triangolo. La potenza trifase, infatti, erogata dal generatore (o assorbita dal carico) a triangolo è uguale a quella erogata
dal generatore (o assorbita dal carico) a stella ad esso equivalente. Consideriamo un generatore (o un carico) connesso a
triangolo ed immaginiamo di sostituire ad esso il suo equivalente a stella, sapendo che:
–
–
–
avremo:
X– =
=
=
=
=
−
⋋−
⋋−
⋋
0
0
0
⋋
⋋
⋋
∙ 0 + – ∙ 0 + – ∙ 0 = F ⋋ − ⋋G ∙ 0 + F
⋋ ∙ F0 − 0 G +
⋋ ∙ F0 − 0 G +
⋋ ∙ F0 − 0 G =
–
⋌
⋌
⋌
=0 −0
=0 −0
=0 −0
−
⋋∙0
⋋
⋋G
∙0 +F ⋋−
+
⋌
⋋∙0 ⋌+
⋋G
⋋∙0
∙0 =
⋌ = X⋌
Analogamente può dimostrarsi per la potenza reattiva trifase quando, al posto dei prodotti scalari, si sostituiscono i
prodotti vettoriali. Pertanto qualunque sia il centro stella al quale è riferita la terna delle tensioni stellate, si ha:
Y=
v ⋀0Z
X=
v
+
v ⋀0Z
+
v ⋀0Z
Il teorema di Aron indica, quindi, come possono esprimersi le potenze di un sistema trifase dissimmetrico e squilibrato
a tre fili, in funzione delle sole grandezze di linea, indipendentemente dal generatore e dal carico.
Riprendendo, infatti, l’espressione generale della potenza attiva trifase:
∙ 0Z +
v
∙ 0Z +
scrivendo l’equazione al nodo (centro stella) per il sistema a tre fili:
v
∙ 0Z
0Z + 0Z + 0Z = 0
e ricavando da quest’ultima, per esempio, 0Z = −0Z − 0Z e sostituendola, si ha:
X=
=
Sistemi Trifase
v
∙ 0Z +
∙ 0Z +
v
∙ F−0Z − 0Z G +
∙ 0Z
v
∙ 0Z = F
v
−
vG
∙ 0Z − F
v
−
vG
∙ 0Z =
∙ 0Z −
∙ 0Z
Pagina 28 di 69
ed analogamente per la potenza reattiva trifase.
In conclusione:
X=
∙ 0Z +
Y=
⋀0Z +
∙ 0Z
⋀0Z
3.5
Misura della potenza nel sistema dissimmetrico e squilibrato
Lo schema di principio per la misura delle potenze in un sistema trifase qualsiasi discende immediatamente dalle
precedenti considerazioni. Inseriamo, infatti, in un sistema a tre fili, tre wattmetri come in figura 25 e creiamo con le tre
bobine voltmetriche il centro stella Os. In virtù del teorema di Aron, la somma delle indicazioni dei wattmetri è uguale
alla potenza attiva trifase del sistema:
X = X™ + X™ + X™ =
v
∙ 0Z +
v
∙ 0Z +
v
∙ 0Z
Figura 25 – Principio generale di misura
E’ chiaro che questo metodo è valido anche per la misura nei sistemi a quattro fili quando si faccia coincidere Os con il
filo neutro.
In pratica, nei sistemi a tre fili la misura si esegue mediante l’uso di soli due wattmetri; facendo infatti coincidere il
centro stella Os con uno dei due fili, ad esempio il filo 2, si ha (figura 26):
Figura 26 – Sistema Aron
v
v
v
Sistemi Trifase
=
=0
=
=−
Pagina 29 di 69
E quindi la potenza trifase P della linea è espressa da:
X=
v
∙ 0Z +
v
∙ 0Z +
v
∙ 0Z =
∙ 0Z +
∙ 0Z
I due prodotti scalari corrispondono proprio alle indicazioni dei wattmetri, avremo quindi:
X = X™ + X™
Pertanto può concludersi che in un qualsiasi sistema a tre fili, la somma delle indicazioni dei due wattmetri inseriti con
il sistema Aron, è uguale alla potenza attiva trifase della linea.
La misura della potenza mediante Aron si esegue dunque in maniera identica sia per i sistemi simmetrici ed equilibrati,
sia per quelli dissimmetrici e squilibrati a tre fili. Questa identità riguarda solo la potenza attiva, perché nei sistemi
dissimmetrici e squilibrati le indicazioni dei due wattmetri non sono sufficienti per misurare la potenza reattiva.
Sia quest’ultima, sia la potenza complessa, possono però misurarsi in Aron con due varmetri e con due vacmetri.
In generale possiamo affermare che per misurare la potenza attiva, la potenza reattiva e la potenza complessa in sistemi
ad n fili, possiamo utilizzare, grazie ad Aron, n-1 wattmetri, n-1varmetri ed n-1 vacmetri.
Sistemi Trifase
Pagina 30 di 69
4
Rifasamento nei sistemi trifase
Rifasare un carico trifase vuol dire inserire in parallelo al carico una batteria di condensatori in modo che la potenza
reattiva complessiva del carico e dei condensatori soddisfi la condizione:
YœŠ
Y•h − Y•ž~|
=
Xœ
X•h
tan : Š =
Figura 27
Si presentano due casi:
1.
Carico equilibrato, collegato a stella (Ÿ) o a triangolo ( ), e tensioni simmetriche o dissimmetriche
Tensioni dissimmetriche
3¡
3¢
9 J + J + J; =
9
+
1¡
1¢
4¡
4¢
9 J + J + J; =
9
Y•h =
+
1¡
1¢
Y•ž~| = £¡ 9 J + J + J ; = £¢ 9
X•h =
Quindi
tan : Š =
tan : =
Š
4¡
9
1¡
4¢
9
1¢
J
+
+
J
+
3¡
9
1¡
+
3¢
9
1¢
J;
J
− £¡ 9
+
J
+
; − £¢ 9
+
+
J
+
J;
+
;
J
;
+
;
+
+
+
+
+
;
4¡
− £¡
1¡
=
3¡
1¡
4¢
;
− £¢
1
= ¢
3¢
1¢
J;
In definitiva sia che i condensatori siano a stella o a triangolo, il valore della loro capacità è indipendente dalle tensioni.
Sistemi Trifase
Pagina 31 di 69
Tensioni simmetriche
3¢
3¡
9 ; = 3 9 ¢;
1¡ ¡
1¢
4¢
4¡
Y•h = 3 9 ¡ ; = 3 9 ¢ ;
1¡
1¢
Y•ž~| = 3 £¡ ¡ = 3 £¢ ¢
X•h = 3
Quindi
tan : Š =
tan : =
Š
3
3
4¡
9
1¡
3
4¢
9
1¢
¡
3
; − 3 £¡
3¡
F
1¡
¢;
¡
G
− 3 £¢
3¢
9
1¢
¢;
¡
¢
4¡
− £¡
1¡
=
3¡
1¡
4¢
− £¢
1
= ¢
3¢
1¢
Anche in questo caso il valore della capacità dei condensatori di rifasamento è indipendente dalle tensioni.
2.
Carico squilibrato (conviene sempre riportare il carico con collegamento a triangolo, rifasare con condensatori
pure a triangolo) e tensioni simmetriche o dissimmetriche
Tensioni dissimmetriche
X•h = 3 9 ; + 3 9 ; + 3 9 ;
1
1
1
Y•h = 4 9 ; + 4 9 ; + 4 9 ;
1
1
1
;
Y•ž~| = £¢ 9
+
+
Quindi
tan : Š =
4 9 ; + 4 9 ; + 4 9 ; − £¢ 9
1
1
1
3 9 ; +3 9 ; +3 9 ;
1
1
1
+
;
+
In questo caso il valore di £¤ dipende dal valore delle tensioni.
Tensioni simmetriche (
=
=
= )
X•h = 3 9 ; + 3 9 ; + 3 9 ;
1
1
1
Y•h = 4 9 ; + 4 9 ; + 4 9 ;
1
1
1
Y•ž~| = 3 £¢
Quindi
tan : Š =
4 9
1
; + 4 9 ; + 4 9 ; − 3 £¢
1
1
3 9 ; +3 9 ; +3 9 ;
1
1
1
¢
=
4
1
+
3
1
4
1
+
+
3
1
4
1
+
− 3 £¢
3
1
Anche in questo caso il valore della capacità dei condensatori di rifasamento è indipendente dalle tensioni.
Sistemi Trifase
Pagina 32 di 69
5
Convenienza dell’utilizzo dei sistemi trifase
Oltre alla fondamentale ragione della scelta del sistema trifase che consiste nella possibilità di generare un campo
rotante e di rendere più semplici e con migliori caratteristiche di funzionamento motori e generatori, sincroni ed
asincroni, una linea trifase risulta anche economicamente conveniente per quanto riguarda l'impiego di rame
Se occorre, infatti, trasmettere una stessa potenza attiva con la medesima tensione, con lo stesso fattore di potenza e con
la stessa densità di corrente nei conduttori, il volume del conduttore impiegato per la linea trifase è inferiore rispetto a
quello impiegato per la linea monofase. In particolare si ha che il volume di rame necessario per la linea trifase è 0,866
volte il volume necessario della corrispondente linea monofase. Si risparmia pertanto circa il 14% di rame.
Indicando con:
abbiamo
X
X
0
0
la potenza attiva trifase;
la potenza attiva monofase;
il valore efficace della corrente di linea nel sistema trifase;
il valore efficace della corrente di linea nel sistema monofase
affinché le due potenze siano uguali, a parità di
Z
X = √3 Z 0 cos :
X = Z 0 cos :
cos :, deve essere
√3 Z 0 cos : =
Z0
cos : → 0 =
0
√3
dovendo lavorare a parità di densità di corrente e quindi con ¦ = ¦ = ¦, essendo:
0
]
0
¦ =
]
¦ =
si ottiene:
0
0
=
¦
¦
0
0
] = =
¦
¦
] =
da cui
0
]
0 ¦ 0
1
√3
= ¦ = / = =
=
= 0.577
0
]
¦ 0
0
3
√3
¦
Quindi, indicando con L la lunghezza della linea, si ottiene:
= 3/] /©
= 2/] /©
da cui
=
Sistemi Trifase
3]
3 √3 √3
= /
=
= 0.866
2]
2 3
2
Pagina 33 di 69
6
Accoppiamenti mutui nei sistemi trifase
Caso generale
Sia dato il seguente sistema trifase, fig. 28:
Figura 28
costituito da tre induttori di induttanza © , © ed © , accoppiati mutuamente con coefficienti di mutua ª , ª
i coefficienti di mutua, come ben sappiamo, sono affetti dal proprio segno.
Scriviamo le espressioni istantanee delle tensioni stellate:
+
«+
«+
«
A
A
A
+
+
+
+
+
+
ed ª ;
=0
=0
=0
e considerando che con i versi assunti delle correnti, cioè tutte entranti dai morsetti contrassegnati con i pallini, le mutue
sono positive, abbiamo:
b8
b8
b8
−ª
−ª
=0
b
b
b
b8
b8
b8
−ª
−ª
=0
«−©
b
b
b
b8
b8
b8
−ª
−ª
=0
«−©
b
b
b
«
cioè:
−©
«
«
«
Sistemi Trifase
b8
b8
b8
+ª
+ª
b
b
b
b8
b8
b8
=©
+ª
+ª
b
b
b
b8
b8
b8
=©
+ª
+ª
b
b
b
=©
Pagina 34 di 69
Ipotizziamo ora di essere a regime permanente sinusoidale e quindi le nostre equazioni diventano:
«
«
«
=
=
=
© 0 +
© 0 +
© 0 +
ª 0 +
ª 0 +
ª 0 +
ª 0
ª 0
ª 0
e queste equazioni sono identiche a quelle che scriveremmo se avessimo da analizzare il seguente sistema elettrico:
Figura 29
Infatti applicando la legge di Ohm generalizzata, otteniamo:
−
−
«−
ª 0 −
ª 0 −
ª 0 −
«
«
da cui:
«
«
«
e ponendo:
abbiamo:
4
=4
=
=
=
=
4 =
ª
«
«
«
Sistemi Trifase
ª 0 −
ª 0 −
ª 0 −
© 0 =0
© 0 =0
© 0 =0
© 0 + ª 0 + ª 0
ª 0 + © 0 + ª 0
ª 0 + ª 0 + © 0
©
4
4 =
=4
©
=
4 =
ª
4
©
=4
=
ª
= 40 + 4 0 + 4 0
= 4 0 + 4 0 + 4 0
= 4 0 + 4 0 + 4 0
Pagina 35 di 69
Quindi la figura 29 la possiamo ora ridisegnare nel seguente modo:
Figura 30 – Circuito equivalente con generatori controllati
Riferendoci al sistema equivalente di figura 30, calcoliamo le tensioni concatenate
=
=
«
«
−
−
«
«
e
:
= 4 0 + 4 0 + 4 0 −F 4 0 + 4 0 + 4 0 G
= 4 0 + 4 0 + 40 − 4 0 − 4 0 − 4 0
= 4 0 + 4 0 + 4 0 −F 4 0 + 4 0 + 4 0 G
= 4 0 + 4 0 + 4 0 − 4 0 − 4 0 − 4 0
Considerando che il sistema è a tre conduttori, abbiamo:
0 +0 +0 =0
da cui:
e sostituendo otteniamo:
0 = −0 − 0
= 4 0 + 4 0 + 40 − 4 0 − 4 0 − 4 0
= 4 F−0 − 0 G + 4 0 + 4 0 − 4 0 − 4 0 − 4 F−0 − 0 G
= 4 0 + 4 0 −2 4 0 + 4 0 + 4 0 − 4 0 − 4 0
= 94 + 4 − 24 ;0 + 94 + 4 − 4 − 4 ;0
= 4 0 + 4
=
=
=
Sistemi Trifase
0 + 4 0 − 4 0 − 4 0 − 4 0
4 0 + 4 F−0 − 0 G + 4 0 − 4 0 − 4 0 − 4 F−0 − 0 G
4 0 + 4 0 − 4 0 − 4 0 + 4 0 + 4 0 −2 4 0
94 + 4 − 4 − 4 ;0 + 94 + 4 − 24 ;0
Pagina 36 di 69
= 94 + 4 − 24 ;0 + 94 + 4 − 4 − 4 ;0
= 94 + 4 − 4 − 4 ;0 + 94 + 4 − 24 ;0
Cioè:
e ponendo
otteniamo
1̅
1̅
1̅ = 94 + 4 − 4 − 4 ;
1̅ = 94 + 4 − 24 ;
= 94 + 4 − 24 ;
= 94 + 4 − 4 − 4 ;
= 1̅ 0 + 1̅ 0
= 1̅ 0 + 1̅ 0
che in forma matriciale è
¬
oppure
¬=-
1̅
1̅
1̅
0
¬ ¬=1̅
0
Ricordiamo come si inverte una matrice, sia data la matrice
o=®
la sua inversa è
o
dove
det9o;
l’esponente ³
UR`9o, / ;
la matrice UR`9o, / ;
UR`9o, / ;
UR`9o, / ;
=
1̅
0
-¬ ¬
1̅
0
1̅
1̅
S
U
¯
®
b
1
UR`9o, / ;
det9o; UR`9o, / ;
¬
¬
UR`9o, / ; ²
UR`9o, / ;
indica il determinante della matrice o;
indica l’operazione di trasposizione righe/colonne;
è la matrice dei cofattori (o dei complementi algebrici);
il cofattore in posizione i, j è definito come UR`Fo, /u G = 9−1;u´ det9µ8QRT 9o, 8, ;;
dove µ8QRT 9o, 8, ; rappresenta il minore di o che si ottiene cancellando la riga i-esima e la colonna j-esima;
+ − +
il segno 9−1;u´ varia nel seguente modo ¶− + −¶ cioè è + se la somma degli indici è pari, negativo se è dispari
+ − +
Sistemi Trifase
Pagina 37 di 69
1̅
1̅
Quindi
1̅
1̅
=
1̅ 1̅
1
1̅
− 1̅ −1̅
²
1
−1̅
1̅
- =
1̅
1̅ 1̅ − 1̅ −1̅
sappiamo inoltre che l’operatore inverso dell’impedenza è l’operatore ammettenza, per cui
1̅
0
¬ ¬=1̅
0
1̅
1̅
¬
=-
¸*
¸*
¬=
1̅ 1̅
¸*
-¬
¸*
1
1̅
− 1̅ −1̅
¬
−1̅
-¬
1̅
1̅
¬ = ··
1̅
1̅
1̅ − 1̅
−1̅
1̅ − 1̅
−1̅
1̅
1̅
1̅
−1̅
1̅ − 1̅ ·
·¬
1̅
1̅ − 1̅
¬
questa relazione ci ricorda la relazione cui si arriva applicando il metodo dei potenziali ai nodi prendendo come
riferimento il nodo 2 (le tensioni sono infatti riferite entrambi al nodo 2).
Cerchiamo quindi di ricavare ora i valori delle ammettenze, collegate a triangolo, per disegnare il circuito equivalente
seguente, figura 31:
Figura 31 – Circuito equivalente a triangolo
Applichiamo il metodo dei potenziali ai nodi 1 e 3, prendendo come riferimento il nodo 2:
e, in forma matriciale,
dove abbiamo posto
Sistemi Trifase
0 = 9•* + •* ;
− •*
0 = −•*
+ 9•* + •* ;
¸*
0
¬ ¬=¸
*
0
¸* = •* + •*
¸* = −•*
¸*
-¬
¸*
¸*
¬
¸* = −•*
= •* + •*
Pagina 38 di 69
da cui segue immediatamente che
1̅
̅
̅
1 1 − 1̅
−1̅
¸* = ¸* = −•* =
1̅ 1̅ − 1̅
1̅
¸* = •* + •* =
1̅ 1̅ − 1̅
¸*
e quindi
= •* + •* =
1̅
− 1̅
1̅ 1̅ − 1̅
1̅ − 1̅
•* =
1̅ 1̅ − 1̅
1̅
•* =
1̅ 1̅ − 1̅
•* =
da queste si ricavano, ovviamente, le corrispettive impedenze collegate a triangolo
1̅
1̅
1̅
1̅ 1̅ − 1̅
1̅ − 1̅
1̅ 1̅ − 1̅
=
1̅ − 1̅
̅
1 1̅ − 1̅
=
1̅
=
e quindi, utilizzando le note formule stella-triangolo, otteniamo le impedenze equivalenti a stella
1̅ =
1̅ =
1̅ =
Sistemi Trifase
1̅
1̅
1̅
1̅ 1̅
+ 1̅ + 1̅
1̅ 1̅
+ 1̅ + 1̅
1̅ 1̅
+ 1̅ + 1̅
Pagina 39 di 69
ed il circuito equivalente di figura 32
Figura 32 – Circuito equivalente a stella
Riepilogando abbiamo:
1̅ =
1̅
1̅
=
1̅ 1̅
+ 1̅ + 1̅
1̅ 1̅ − 1̅
1̅ − 1̅
1̅ =
1̅
=
1̅ = 94 + 4 − 24 ;
1̅ = 94 + 4 − 4 − 4 ;
4
4 =
=4 =
©
ª
1̅
4
1̅ 1̅
+ 1̅ + 1̅
1̅ 1̅ − 1̅
1̅ − 1̅
4 = ©
=4 =
1̅ =
1̅
1̅
=
1̅ 1̅
+ 1̅ + 1̅
1̅ 1̅
1̅
− 1̅
1̅ = 94 + 4 − 4 − 4 ;
1̅ = 94 + 4 − 24 ;
ª
4 = ©
4 =4 =
ª
Figura 33 – Equivalenza complessiva
Sistemi Trifase
Pagina 40 di 69
Caso particolare
Ipotizzando ora che sia le induttanze, sia le mutue, siano uguali tra loro, cioè:
© =© =© =©
avremo
quindi
1̅
1̅
da cui
inoltre
1̅
=
4 = 4 = 4 = 4A =
©
= 94A + 4A − 24 ; = 2 94A − 4 ;
= 94A + 4 − 4 − 4 ; = 94A − 4 ;
1̅
= 1̅
= 2 94A − 4 ;
b ª
=ª
4
=ª
=4
=ª
=4
=4 =
ª
1̅ = 94A + 4 − 4 − 4 ; = 94A − 4 ;
1̅ = 94A + 4A − 24 ; = 2 94A − 4 ;
1̅
= 1̅
= 94A − 4 ;
1̅ 1̅ − 1̅
2 94A − 4 ;2 94A − 4 ; − L 94A − 4 ;M
−494A − 4 ; + 94A − 4 ;
−394A − 4 ;
=
=
=
̅
̅
94
;
2 A − 4 − 94A − 4 ;
94A − 4 ;
94A − 4 ;
1 −1
= 394A − 4 ;
e, analogamente
ed infine
1̅
1̅ =
Sistemi Trifase
= 1̅
= 1̅
= 1∆̅ = 394A − 4 ;
1∆̅
1∆̅
=
= 94A − 4 ; =
3
31∆̅
9© − ª;
Pagina 41 di 69
Verifica
Verifichiamo, per altra via, che queste relazioni siano valide in modo da avere anche la conferma della validità delle
relazioni generali.
Scriviamo quindi le espressioni istantanee delle tensioni stellate, in questo caso, anche baricentriche e l’equazione al
nodo 0, centro stella o baricentro:
= ©0 +
= ©0 +
©0 +
« =
0 +0 +0 =0
«
«
considerando che
si ha
=
« =
« =
«
C.V.D.
ª0 +
ª0 +
ª0 +
ª0
ª0
ª0
0 + 0 = −0
0 + 0 = −0
0 + 0 = −0
©0 +
©0 +
©0 +
ª0 +
ª0 +
ª0 +
ª0 =
ª0 =
ª0 =
©0 −
©0 −
©0 +
ª0 −
ª0 −
ª0 −
ª0 +
ª0 +
ª0 −
ª0 =
ª0 =
ª0 =
9© − ª;0 = 1̅ 0
9© − ª;0 = 1̅ 0
9© − ª;0 = 1̅ 0
Quindi
Figura 34 – Equivalenza complessiva carico equilibrato
Sistemi Trifase
Pagina 42 di 69
Consideriamo adesso lo stesso circuito ma con l’aggiunta del conduttore neutro, figura 35
Figura 35 – Mutue con neutro
Le equazioni dell’equilibrio elettrico sono analoghe a quelle scritte prima con l’unica differenza che ora risulta
quindi, con analoghe considerazioni abbiamo
=
=
«
« =
«
©0 +
©0 +
©0 +
ª0 +
ª0 +
ª0 +
ª0 =
ª0 =
ª0 =
0 + 0 + 0 + 0~ = 0
©0 −
©0 −
©0 +
ª0 −
ª0 −
ª0 −
ª0 −
ª0 −
ª0 −
da cui segue immediatamente il circuito equivalente di figura 36
ª0~ +
ª0~ +
ª0 −
ª0 =
ª0 =
ª0~ =
9© − ª;0 −
9© − ª;0 −
9© − ª;0 −
ª0~
ª0~
ª0~
Figura 36 – Circuito equivalente con neutro
Sistemi Trifase
Pagina 43 di 69
7
Studio generale dei sistemi trifase
7.1
Rappresentazione matriciale delle grandezze trifase
In simboli matriciali, una terna qualsiasi di vettori Fo , o , o G è normalmente rappresentata mediante la matrice
colonna i cui elementi sono i vettori stessi della terna:
o
‖o ‖ = · o ·
o
Solo per alcuni calcoli, la terna viene anche rappresentata mediante la relativa matrice riga:
‖o‖ = |o
o
o |
Quindi nella rappresentazione matriciale, le terne delle tensioni F ,
trifase (figura 37a) sono normalmente indicate mediante i simboli:
‖ ‖=· ·
,
G e delle correnti F0 , 0 , 0 G di un circuito
0
‖0 ‖ = · 0 ·
0
che rispettivamente sono matrice colonna delle tensioni e matrice colonna delle correnti.
Figura 37
E’ evidente perciò come sia possibile, qualora fosse utile, rappresentare il sistema trifase mediante uno schema
monofase equivalente (figura 37b) dove le grandezze sono rappresentate da matrici di vettori.
Sistemi Trifase
Pagina 44 di 69
Somma di terne di vettori:
in forma matriciale:
Fo , o , o G + F¼ , ¼ , ¼ G = Fo + ¼ , o + ¼ , o + ¼ G
o
¼
o +¼
‖o‖ + ‖¼ ‖ = ·o · + ·¼ · = ·o + ¼ · = ‖o + ¼ ‖
o
¼
o +¼
0h
0m
0h + 0m
Ad esempio, le correnti di una linea trifase che convoglia le correnti di due linee in parallelo (figura 38a), nella
rappresentazione matriciale si esprimono:
½0h ½ + ½0 m ½ = ·0h · + ·0m · = ·0h + 0m · = ‖0h + 0 m ‖
0h
0m
0h + 0m
Figura 38
Che possono dar luogo, ovviamente, allo schema monofase equivalente di figura 38b.
Sistemi Trifase
Pagina 45 di 69
Prodotto di una terna di vettori per un numero:
in forma matriciale:
¾ ∙ Fo , o , o G = F¾o , ¾o , ¾ o G
¾o
¾ ∙ ‖o‖ = ·¾o · = ½¾o½
¾o
Ad esempio le tensioni , , , agli estremi delle fasi di un carico equilibrato, di impedenza per fase 1̅, le cui
correnti sono 0 , 0 e 0 (figura 39a),
Figura 39
possono esprimersi in forma matriciale come:
1̅0
0
‖ ‖ = · · = ¿1̅0 ¿ = 1̅ ¿0 ¿ = 1̅‖0 ‖
1̅0
0
E quindi mediante il relativo schema monofase equivalente.
Prodotto di una terna di vettori per una terna di numeri:
9¾ , ¾ , ¾ ; ∙ Fo , o , o G = F¾ o , ¾ o , ¾ o G
in forma matriciale questo risultato si ottiene moltiplicando la matrice diagonale formata con la terna dei numeri
¾ ,¾ ,¾ :
per la matrice colonna della terna dei vettori
¾
‖¾ ‖ = ¶ 0
0
¾
‖¾ ‖ ∙ ‖o ‖ = ¶ 0
0
Sistemi Trifase
0
¾
0
0
¾
0
0
0¶
¾
o
¾ o
0
0 ¶ ∙ ·o · = ·¾ o ·
¾
o
¾ o
Pagina 46 di 69
Ad esempio le tensioni
e 0 (figura 39b),
,
,
, agli estremi delle fasi di un carico squilibrato 1̅ , 1̅ , 1̅ , percorso dalle correnti 0 , 0
Figura 39
sono rappresentate in forma matriciale:
1̅ 0
1̅
‖ ‖ = · · = ¿1̅ 0 ¿ = ¿ 0
0
1̅ 0
dove ‖1̅‖ è la matrice diagonale delle impedenze del carico.
0
1̅
0
0
0
0 ¿ ∙ ¿0 ¿ = ‖1̅ ‖ ∙ ‖0 ‖
1̅
0
Prodotto di una terna di vettori per una tripla terna di numeri:
¾
À¾
¾
¾
¾
¾
¾
¾ Á ∙ Fo , o , o G =
¾
= ÂF¾ o + ¾ o + ¾ o G
F¾ o + ¾ o + ¾ o G F¾ o + ¾ o + ¾ o GÃ
in forma matriciale:
¾
‖¾‖ ∙ ‖o‖ = ¶¾
¾
¾
¾
¾
o
¾ o +¾ o +¾ o
¾
¾ ¶ ∙ ·o · = ¿ ¾ o + ¾ o + ¾ o ¿
¾
¾ o +¾ o +¾ o
o
Questo calcolo, nei sistemi trifase, è quello che si esegue per calcolare la tensione agli estremi delle fasi di un carico
con accoppiamento induttivo fra fase e fase (figura 40)
Figura 40
Sistemi Trifase
Pagina 47 di 69
̅ il coefficiente di mutua
Infatti, indicando con 1̅ , 1̅ , 1̅ le impedenze proprie delle fasi (auto impedenze) e con 1IÄ
induzione della fase h rispetto alla fase k moltiplicato per
(mutue impedenze), si ha:
= 1̅ 0 + 1̅ 0 + 1̅ 0
= 1̅ 0 + 1̅ 0 + 1̅ 0
= 1̅ 0 + 1̅ 0 + 1̅ 0
per cui, in forma matriciale, la terna delle tensioni è legata alla terna delle correnti dalla relazione:
“ ‖ ∙ ‖0 ‖
‖ ‖ = ‖1
dove
1̅
“‖ = ¿1̅
‖1
1̅
1̅
1̅
1̅
1̅
1̅ ¿
1̅
Si dice matrice quadrata delle auto e mutue impedenze.
Come è facile rilevare dalle equazioni precedenti, i nove valori delle auto e mutue impedenze, che costituiscono gli
elementi della matrice, possono essere determinati sperimentalmente con semplici misure, inviando successivamente
una corrente in ciascuna fase e misurando ogni volta le tensioni.
Indicando con
a)
b)
c)
∗
∗
∗
,
,
,
∗
∗
∗
e
e
e
∗
∗
∗
le tensioni misurate quando la sola fase 1 è percorsa dalla corrente 0 ∗ ;
le tensioni misurate quando la sola fase 2 è percorsa dalla corrente 0 ∗ ;
le tensioni misurate quando la sola fase 3 è percorsa dalla corrente 0 ∗
dal sistema scritto prima:
= 1̅ 0 + 1̅ 0 + 1̅ 0
= 1̅ 0 + 1̅ 0 + 1̅ 0
= 1̅ 0 + 1̅ 0 + 1̅ 0
abbiamo che le auto e mutue impedenze del sistema sono:
a)
b)
c)
Sistemi Trifase
∗
∗
∗
∗
∗
∗
∗
∗
∗
= 1̅ 0
= 1̅ 0 ∗
= 1̅ 0 ∗
∗
= 1̅ 0 ∗
= 1̅ 0 ∗
= 1̅ 0 ∗
= 1̅ 0 ∗
= 1̅ 0 ∗
= 1̅ 0 ∗
da cui
da cui
da cui
1̅
1̅
1̅
1̅
1̅
1̅
1̅
1̅
1̅
=
∗
5••
=
5 ∗•
=
\•∗
5 ∗•
\•∗
\•∗
=
5•∗
=
5∗
=
\∗
5∗
\∗
\∗
=
5•∗
=
5∗
=
\∗
5∗
\∗
\∗
Pagina 48 di 69
Rappresentazione matriciale della legge di Ohm, dei principi di Kirchhoff e della potenza trifase
Riassumendo le precedenti considerazioni, si rileva che la legge di Ohm per i sistemi trifase può essere espressa in
forma matriciale come:
‖ ‖ = ‖1̅‖ ∙ ‖0 ‖
Ed esprime il legame fra le grandezze di fase. La matrice quadrata delle auto e mutue impedenze si riduce alla matrice
diagonale nel caso di carichi privi di accoppiamento induttivo ed al solo valore 1̅ delle impedenze nel caso di carichi
equilibrati
Carichi con accoppiamenti induttivi fra le fasi
Carichi senza accoppiamenti induttivi fra le fasi
‖ ‖ = ‖1̅ ‖ ∙ ‖0 ‖
1̅
“‖ = ¿1̅
‖1
1̅
1̅
1̅
1̅
1̅
1̅ ¿
1̅
Carichi squilibrati
Carichi equilibrati
‖ ‖ = ‖1̅‖ ∙ ‖0 ‖
‖ ‖ = 1̅ ∙ ‖0 ‖
1̅
“‖ = ¿ 0
‖1
0
0
1̅
0
0
0 ¿
1̅
Matrice diagonale delle impedenze
Matrice quadrata delle auto e mutue impedenze
1̅ = 1̅
= 1̅
= 1̅
Valore comune delle impedenze
Estendendo le considerazioni sulla somma di due terne di correnti, illustrate nella figura 29, ad un numero qualsiasi di
9Ä; 9Ä; 9Ä;
terne ed indicando con 0 , 0 , 0 le correnti della terna k-sima (per il segno valgono le convenzioni dei nodi nei
sistemi monofase), il primo principio di Kirchhoff applicato ad un nodo di una rete trifase può essere espresso in forma
matriciale dalla relazione:
Æ ½0 9Ä; ½ = 0
Ä
9Ä;
9Ä;
9Ä;
9Ä;
9Ä;
9Ä;
9Ä;
9Ä;
9Ä;
Considerando poi una maglia di una rete trifase nella quale
,
,
, 0 , 0 , 0 , 1̅ , 1̅ , 1̅
siano
rispettivamente le tensioni, le correnti e le impedenze relative alle tre fasi (con o senza accoppiamento induttivo) del
lato k-simo della maglia (adottando per il segno delle tensioni e delle correnti le stesse convenzioni adottate per le
maglie dei circuiti monofase) il secondo principio di Kirchhoff si esprime in forma matriciale con la relazione:
Æ F½
Ä
9Ä;
½ − ½1̅ 9Ä; ½ ∙ ½0 9Ä; ½G = 0
Infine, sappiamo che il regime energetico di un sistema trifase può essere compiutamente definito mediante la potenza
complessa:
]̅ = ]̅ + ]̅ + ]̅ = X + Y + X + Y + X + Y =
∙ 0_ +
∙ 0_ +
∙ 0_
Rappresentando la potenza mediante matrice ad un solo elemento, si rileva che essa è uguale al prodotto di una matrice
riga per una matrice colonna:
|]̅| = |
∙ 0_ +
∙ 0_ +
∙ 0_ | = |
0_
| ∙ ¿0_ ¿ = ‖ ‖ ∙ ‖0Ç‖
0_
Pertanto, in forma matriciale, la potenza complessa di un qualsiasi sistema trifase è rappresentata dal prodotto della
matrice riga delle tensioni per la matrice colonna dei coniugati delle correnti.
Sistemi Trifase
Pagina 49 di 69
7.2
L’algebra delle sequenze
I moderni metodi di analisi per lo studio generale del comportamento dei sistemi trifase (simmetrici, dissimmetrici,
equilibrati, squilibrati, puri o spuri) sono basati su procedimenti di scomposizione dei sistemi trifase di grandezze in
terne componenti , la cui somma riproduce il sistema considerato.
L’efficacia di tali metodologie consiste dalla possibilità da essi offerta, una volta operata la scomposizione, di
determinare disgiuntamente il comportamento del sistema in presenza di ognuna delle componenti, indipendentemente
dalle altre, e di ricostruire poi il regime globale del sistema applicando il principio di sovrapposizione degli effetti.
Il procedimento di scomposizione dei sistemi trifase più usato è quello di Fortescue. In esso due delle componenti sono
terne simmetriche.
Allo scopo di rendere più agile e rapido il calcolo, faremo uso di un particolare metodo di rappresentazione delle terne
simmetriche di grandezze, indicato comunemente con il nome di algebre delle sequenze.
Fra i vari fattori di rotazione visti, occorre menzionare in particolare il fattore che, applicato ad un vettore, ne ruota la
direzione di 120° in anticipo, lasciandone immutata l’intensità Questo fattore, che indicheremo con l è rappresentato
dal numero complesso costante:
l=
1
√3
=− +
2
2
lÈ =
1
√3
=− −
2
2
Il cui complesso coniugato è ovviamente:
Le successive potenze di l con esponente intero:
l« = 1
l =
l =
<
'
l =
É
l =
<
l =
Ë
«
=1
=l
=l
Riproducono ciclicamente all’infinito sempre la stessa terna di valori:
l« = 1
l=
l =
<
l' =
l =
Ê
l =
É
<
'
=1
=l
=l
1
√3
=− +
2
2
1
√3
=− −
= lÈ
2
2
Che, riportai sul piano di Gauss (figura 41), corrispondono ai vertici di un triangolo equilatero e che rappresentano le tre
radici cubiche dell’unità.
√3
2
√3
2
Figura 41
Sistemi Trifase
Pagina 50 di 69
Ricordando che le radici cubiche dell’unità, dovendo soddisfare la relazione:
Coincidono con le radici dell’equazione.
/ =1
/ − 1 = 9/ − 1;9/ + / + 1; = 0
dalla quale, annullando il primo fattore si ottiene:
ed annullando il secondo:
/ =1
√3
Ñ 1
−1 ± √1 − 4 −1 ± √−3 −1 ± √3 Ï− 2 + 2
Ì=
=
=
=
2
2
2
√3
Ð 1
/
Ï− −
2
Î 2
/
E’ facile rilevare che tale terna di numeri gode della proprietà che la loro somma è nulla:
l« + l + l = 1 + l + l =
=1−
1
1
√3 1
√3
√3 √3
+
− −
= 1− + y − z=0
2
2
2
2
2
2
2
Consideriamo le tre potenze di l 91; l; l ; che, al crescere dell’esponente, si riproducono ciclicamente all’infinito. I
loro punti rappresentativi sul piano di Gauss si susseguono, lungo la circonferenza unitaria, secondo il senso di
rotazione orario (figura 42), quando le potenze si succedono nell’ordine:
1; l ; l
Figura 42
Si susseguono invece secondo il senso di rotazione antiorario quando le potenze si succedono nell’ordine.
1; l; l
Sistemi Trifase
Pagina 51 di 69
Chiameremo allora sequenza diretta 9’Ó ; la terna dei tre fattori di rotazione rappresentati dalle potenze di l prese
nella successione corrispondente al senso orario e sequenza inversa 9’Ô ;, la stessa terna presa nella successione
corrispondente al senso antiorario (figura 33).
In simboli matriciali, esse sono rappresentate da due matrici colonna i cui elementi sono fattori di rotazione:
1
‖]| ‖ = ¶l ¶
l
1
‖]u ‖ = ¶l ¶
l
Chiameremo, infine, sequenza omopolare 9’Õ ; la terna costituita da tre elementi tutti uguali all’unità:
1
‖]ž ‖ = ¶1¶
1
Il prodotto di una sequenza per un vettore è costituito dalla terna di vettori ottenuti applicando al vettore dato ognuno
dei tre fattori di rotazione della sequenza.
Pertanto se la sequenza è diretta, il prodotto è costituito da una terna simmetrica di vettori che si susseguono nell’ordine
ciclico diretto e che ha come primo vettore il vettore dato Ö|
Ö|
Ö|
1
‖]| ‖ ∙ Ö| = ¶l ¶ ∙ Ö| = ¿l Ö| ¿ = ·Ö|
l
lÖ|
Ö
|
<
Ö|
· = ¿Ö| ¿ = ½Ö| ½
Ö|
Se la sequenza è inversa, il prodotto è costituito da una terna simmetrica di vettori che si susseguono nell’ordine ciclico
inverso e che ha come primo vettore il vettore dato Öu
Öu
Öu
1
‖]u ‖ ∙ Öu = ¶l ¶ ∙ Öu = ¿lÖu ¿ = ·Öu
l
l Öu
Ö
u
<
Öu
· = ¿Öu ¿ = ½Öu ½
Öu
Se infine la sequenza è omopolare, il prodotto è costituito da una terna di vettori tutti uguali al vettore dato ož
Öž
1
‖]ž ‖ ∙ Öž = ¶1¶ ∙ Öž = ¿Öž ¿ = ½Öž ½
1
Öž
Le precedenti considerazioni indicano chiaramente la possibilità di rappresentare ogni terna di vettori di sequenza
diretta, o inversa, o omopolare, mediante il prodotto della relativa sequenza per uno qualsiasi dei vettori della terna
scelto ad arbitrio. Il vettore scelto come riferimento, il cui prodotto per la sequenza dà luogo all’intera terna, sarà
chiamato vettore base della terna.
Per gli usi pratici è di fondamentale importanza la considerazione della matrice quadrata delle sequenze o matrice del
Fortescue. Essa si ottiene formando una matrice quadrata con le tre matici colonna rappresentative delle sequenze
]ž , ]| ]u :
1
‖]‖ = ¶1
1
Sistemi Trifase
1
l
l
1
l¶
l
Pagina 52 di 69
La matrice è simmetrica e il suo determinante ha valore:
|]| = 19l ∙ l − l ∙ l; − 191 ∙ l − l ∙ 1; + 191 ∙ l − l ∙ 1; = l < − l − l + l + l − l = l < − 3l + 2l
Ricordando (figura 32) che l < = l otteniamo:
|]| = l < − 3l + 2l = l − 3l + 2l = 3l − 3l = 39l − l ; =
1
1
1 1
√3
√3
√3
√3
= 3 wy− +
z − y− −
zx = 3 y− + +
+
z = 3 √3
2
2
2
2
2
2
2 2
La matrice che si ottiene dalla precedente scambiando di posto la seconda con la terza riga (oppure la seconda con la
terza colonna) e dividendo per 3, è la matrice inversa della precedente e si chiama matrice quadrata inversa delle
sequenze.
‖]‖
=
1 1
¶1
3
1
1
l
l
1
l ¶
l
Si ha, infatti, ricordando che il prodotto di una matrice per la sua inversa è uguale alla matrice identità::
‖]‖ ∙ ‖]‖
1
= ¶1
1
1
l
l
1
= ¶0
0
1 1 1 1
l ¶ ∙ ¶1 l
3
l
1 l
0 0
1 0¶ = ‖×‖
0 1
1
1 1+1+1
l ¶ = ¶1 + l + l
3
l
1+l+l
1+l+l
1+1+1
1+l +l
1+l +l
1 3
1 + l + l ¶ = ¶0
3
0
1+1+1
0
3
0
0
0¶
3
7.3
Scomposizione di un sistema trifase di grandezze
Come già detto, fra i vari metodi di scomposizione dei sistemi trifase di grandezze in terne componenti, utilizzeremo il
metodo del Fortescue, nel quale le tre componenti sono costituite da due terne simmetriche e da una omopolare. Questo
metodo è basato sul teorema del Fortescue, il quale afferma che: ogni terna di vettori qualsiasi è sempre univocamente
scomponibile in tre terne, una di sequenza omopolare, una di sequenza diretta ed una di sequenza inversa.
Vale a dire che data una terna qualsiasi di vettori Fo , o , o G, esiste sempre uno ed uno solo sistema di tre vettori Öž ,
Ö| , Öu , i quali considerati come vettori basi di tre terne rispettivamente di sequenza omopolare, diretta e inversa,
danno luogo a tre terne ‖]ž ‖ ∙ Öž , ‖]| ‖ ∙ Ö| e ‖]u ‖ ∙ Öu , la cui somma riproduce la terna data Fo , o , o G.
o
Öž
Ö|
Öu
Ö ž + Ö | + Öu
1
1
1
1
¿o ¿ = ¶1¶ Öž + ¶l ¶ Ö| + ¶l ¶ Öu = ¿Öž ¿ + ¿l Ö| ¿ + ¿lÖu ¿ = ¿Öž + l Ö| + lÖu ¿ = ¶1
1
l
l
1
Öž
lÖ|
l Öu
Öž + lÖ| + l Öu
o
O anche:
1
l
l
Öž
1
l ¶ ∙ ¿Ö | ¿
l
Öu
½o½ = ‖]‖ ∙ ‖Ö ‖
Dove ‖]‖ è, ovviamente, la matrice quadrata delle sequenze.
Il teorema si dimostra immediatamente uguagliando fra loro gli elementi corrispondenti delle due matrici colonna:
Ñ
Ï
o = Ö ž + Ö | + Öu
o = Öž + l Ö| + lÖu
Ð
Ï
Îo = Öž + lÖ| + l Öu
Sistemi Trifase
Pagina 53 di 69
Questo è un sistema lineare di tre equazioni che stabilisce un legame biunivoco tra la terna dei vettori o , o , o e la
terna dei vettori base delle terne componenti Öž , Ö| , Öu . Di conseguenza il sistema consente, dati Öž , Ö| e Öu di
ricavare o , o o e, viceversa, dati o , o o di dedurre i primi:
dove ‖]‖ è la matrice inversa delle sequenze.
Infatti da
Moltiplicando ambo i membri per ‖]‖
Si ha pertanto:
‖Ö ‖ = ‖]‖
∙ ½o½
½o½ = ‖]‖ ∙ ‖Ö ‖
si ottiene:
‖]‖
∙ ½o½ = ‖]‖
∙ ‖]‖ ∙ ‖Ö ‖ = ‖Ö ‖
1
ÑÖž = Fo + o + o G
3
Ï
1
Ö| = Fo + lo + l o G
3
Ð
1
ÏÖ
Fo + l o + lo G
Î u= 3
Infatti la relazione matriciale:
‖Ö ‖ = ‖]‖
significa ovviamente:
Öž
1
· · 1
= ¶1
Ö
|
· · 3
1
Öu
1
l
l
∙ ½o½
1
Fo + o + o G
3
o
·1
1
l ¶ ∙ ¿o ¿ = Fo + lo + l o
·3
l
o
1
Fo + l o + lo
3
·
G
·
G
Le precedenti relazioni stabiliscono dunque una corrispondenza biunivoca fra terne qualsiasi di vettori e sistemi di tre
terne, rispettivamente di sequenza omopolare, diretta e inversa.
Ogni sistema di tre vettori è perciò compiutamente individuato e determinato dalle corrispondenti terne nelle quali esso
è decomponibile, che vengono chiamate le sue componenti simmetriche. E poiché, come già visto, ciascuna
componente simmetrica è individuata dal suo vettore base, la rappresentazione delle terne di vettori Fo , o , o G
mediante le loro componenti simmetriche, viene effettuata in base alle relazioni di corrispondenza:
‖o‖ = ‖]‖ ∙ ‖Ö ‖
‖Ö ‖ = ‖]‖
Sistemi Trifase
∙ ½o½
Pagina 54 di 69
Proprietà delle componenti simmetriche
Se Öž , Ö| e Öu sono i vettori base delle componenti simmetriche della terna o , o
complesso, si ha ovviamente:
‖]‖
∙ ½¾o½ = ¾‖]‖
o e k è un numero reale o
∙ ½o½ = ¾‖Ö ‖ = ‖¾ Ö ‖
Cioè i vettori base delle componenti simmetriche della terna ottenuta moltiplicando per k una terna di vettori, sono
uguali ai vettori base delle componenti simmetriche di questa, moltiplicati per k.
Se Fo , o , o G e F¼ , ¼ , ¼ G sono due terne qualsiasi e FÖž , Ö| , Öu G e Fℬž , ℬ| , ℬu G sono i vettori base delle
rispettive componenti simmetriche, si ha:
‖]‖
∙ ½o + ¼ ½ = ‖]‖
∙ ½o½ + ‖]‖
∙ ½¼ ½ = ‖Ö ‖ + ‖ℬ ‖ = ‖Ö + ℬ ‖
Vale a dire che i vettori base delle componenti simmetriche della somma di due terne di vettori, sono uguali alla somma
dei corrispondenti vettori base delle componenti simmetriche delle terne addendi.
Altra proprietà che si utilizza nella pratica del calcolo è quella relativa alle terne coniugate.
Consideriamo una terna di vettori Fo , o , o G ed i vettori base FÖž , Ö| , Öu G delle loro componenti simmetriche. E’
facile dimostrare che se con Ö‘ž , Ö‘| , Ö‘u indichiamo i vettori base delle componenti simmetriche della terna dei
vettori Fo_ , o_ , o_ G coniugati dei primi, si ha:
Ñ
Ï
Ö‘| =
Ð
Ï
Î Ö‘u =
Infatti se
o =o
o =o
o =o
si ha
o_ = o
o_ = o
o_ = o
Si deduce che:
Ö‘ž =
e poiché
Sistemi Trifase
Ö_u
Ö_|
Ù•
Ù
Ù
Ù•
Ù
Ù
1
1
Fo_ + o_ + o_ G = Fo
3
3
Öž =
si ottiene:
Ö‘ž = Ö_ž
1
1
Fo + o + o G = Fo
3
3
Ù•
+o
Ù•
+o
Ù
Ù
+o
+o
Ù
Ù
G
G
Ö‘ž = Ö_ž
Pagina 55 di 69
Analogamente:
Ö‘| =
e poiché
Öu =
1
1
Fo_ + lo_ + l o_ G =
o
3
3
1
Ù•
= No
+o
3
1
1
Fo + l o + lo G =
o
3
3
Ù•
+o
+o
Ù
Ù
Ù•
<
"
+o
si conclude che
Ù
<
Ù
+o
+o
"
Ù
O=
Ù
1
No
3
<
=
Ù•
1
No
3
+o
Ù•
Ù ´
+o
"
Ù ´
+o
"
+o
<
Ù ´ "
Ù ´
<
O
"
O
Ö‘| = Ö_u
Con analogo ragionamento si ha:
Ö‘u = Ö_|
Riassumendo, si ha quindi che:
‖]‖
Ö_ž
_
∙ ½o½ = ¿Ö_u ¿
Ö_|
Vale a dire, le componenti simmetriche ella terna coniugata di una terna di vettori sono uguali ai coniugati delle
componenti simmetriche della terna data, però con uguaglianze incrociate fra le componenti dirette e quelle inverse.
Se la terna dei vettori considerata,costituisce un sistema puro Fo + o + o = 0G, la sua componente simmetrica di
sequenza omopolare è necessariamente uguale a zero:
Öž =
1
Fo + o + o G = 0
3
E viceversa; vale a dire, la condizione necessaria e sufficiente affinché una terna di vettori sia pura è che la sua
componente omopolare sia nulla.
In tal caso, chiaramente, il centro stella della terna dei vettori considerati coincide con il baricentro del triangolo che ha
per vertici gli estremi dei vettori stessi (figura 43).
Figura 43
Sistemi Trifase
Pagina 56 di 69
In generale, invece, quando la terna è spuria il vettore base della sua componente omopolare, essendo uguale alla media
aritmetica dei tre vettori (cfr formula pag 24), è rappresentato dal segmento che unisce il centro stella della terna con il
baricentro del triangolo che ha per vertici gli estremi dei vettori stessi.
La presenza della componente omopolare è dunque l’elemento indicativo della impurezza della terna stessa, si assume
di conseguenze, come grado di impurezza 9ÚÔ ; di una terna di vettori il rapporto fra le ampiezze dei vettori base della
componente omopolare e della componente diretta.
Ûu =
Öž
Ö|
Prendiamo ora in esame terne di grandezze sinusoidali rappresentate da stelle di vettori a vertici comuni, le quali hanno
gli estremi dei vettori corrispondenti che coincidono in tre punti 1, 2, e 3 comuni a tutte le terne (figura 44).
Figura 44
Indichiamo con ¼ , ¼ e ¼ i vettori concatenati, rappresentati dai lati del triangolo formato dai vertici comuni a tutte le
terne, attribuendo per indice, ad ognuno di essi, il numero corrispondente al vertice opposto.
¼ = o − o = oŠ − oŠ = ⋯
ܼ = o − o = oŠ − oŠ = ⋯
¼ = o − o = oŠ − oŠ = ⋯
Indichiamo ora con Öž , Ö| , Öu , i vettori base delle componenti simmetriche della terna generica Fo , o , o G
avente i vertici nei punti 1, 2 e 3 e con ℬž , ℬ| , ℬu i vettori base delle componenti simmetriche della terna dei vettori
concatenati ¼ , ¼ e ¼ :
‖Ö ‖ = ‖]‖
‖ℬ ‖ = ‖]‖
Si rileva facilmente che valgono le seguenti relazioni:
∙ ½o½
∙ ½¼ ½
ℬž = 0
Ýℬ| = − √3 Ö|
e, quindi, reciprocamente:
ℬu = √3 Öu
ÑÖ| =
√3
ℬ|
ÐÖ = −
ℬu
Î u
√3
Sistemi Trifase
Pagina 57 di 69
Infatti abbiamo:
ℬ| =
ℬž =
1
F¼ + ¼ + ¼ G = 0
3
1
1
F¼ + l¼ + l ¼ G = ÂFo − o G + lFo − o G + l Fo − o GÃ =
3
3
1
Âo 9l − l; + lo 9l − l; + l o 9l − l;Ã =
3
1
= 9l − l;Âo + lo + l o à = 9l − l;Ö| = − √3Ö|
3
=
e con calcolo analogo:
ℬu = √3Öu
Osserviamo che poiché tali relazioni sono state ottenute per una stella generica, esse sono valide per tutte le stelle dei
vettori aventi i vertici nei punti 1, 2 e 3. E poiché i vettori concatenati sono comuni a tutte, si conclude che in ogni
sistema di terne di vettori a vertici comuni, tutte quante le terne hanno le stesse componenti simmetriche diretta ed
inversa e, perciò, si differenziano solo per la componente omopolare.
Infatti, per quanto detto, la componente omopolare è determinata dalla posizione del centro stella di ciascuna stella.
Pertanto se di una terna di vettori si conosce solo la relativa terna concatenata (si conoscono cioè i vertici 1, 2 e 3 della
stella dei vettori, ma non il centro stella O), risultano determinate le sue componenti simmetriche diretta ed inversa, ma
rimane indeterminata la componente omopolare, salvo che per la terna baricentrica per la quale, chiaramente, la
componente omopolare è nulla.
E’ evidente che una terna di vettori di senso ciclico diretto è simmetrica quando si identifica con la propria
componente simmetrica di sequenza diretta, cioè quando le sue componenti simmetriche omopolare ed inversa sono
nulle (Öž = 0, Öu = 0;. Di conseguenza una terna le cui componenti omopolare ed inversa sono diverse da zero è
ovviamente asimmetrica ed è logico reputare che essa si discosti tanto più dalle condizioni di simmetria, quanto
maggiore è l’ampiezza dei vettori base, Öž Öu , di tali componenti.
Ö
Il grado di impurezza Ûu = Þ , prima definito, rappresenta l’indice quantitativo della dissimmetria di cui risulta affetta
Öß
la terna a causa della presenza di una componente omopolare non nulla. Ed è quindi chiaro che nei sistemi trifase nei
quali è nulla la componente inversa, Ûu indica la asimmetria globale del sistema. La dissimmetria prodotta invece nella
terna dalla presenza di una componente inversa non nulla, si valuta quantitativamente mediante un indice definito dal
rapporto fra l’ampiezza del vettore base della componente inversa e quella del vettore base della componente diretta,
che si dice grado di squilibrio 9Ú‚ ; della terna:
Ûv =
Öu
Ö|
Nei sistemi puri nei quali come visto Öž = 0 e Ûu = 0 (ad esempio sistemi a tre conduttori), Ûv indica ovviamente
l’asimmetria globale del sistema.
Pertanto, nei sistemi puri:
Ûv =
Öu
àÖ
|
0
Öu
0
Ö|
∞
≠0
0
1
= Ö|
= Öu
Sistemi Trifase
≠0
Terna simmetrica
Terna simmetrica senso ciclico inverso
I vettori della terna hanno tutti uguale direzione (ma
non uguale verso) e corrispondono, nel loro
complesso, ad un sistema monofase
Pagina 58 di 69
7.4
Analisi dei sistemi trifase mediante le componenti simmetriche
Ci riferiamo al caso più generale e precisamente ai sistemi trifase dissimmetrici e squilibrati a quattro conduttori;
l’analisi di tutti gli altri casi può dedursi, evidentemente, da questo caso più generale.
Indichiamo con ,
le tensioni dei conduttori rispetto al neutro; con
,
le tensione di linea; con 0 ,
0 0 le correnti di linea ed indichiamo con ½á ½, ½áZ ½ ed ½ℐ ½ le matrici colonna dei vettori base delle rispettiva
componenti simmetriche (figura 45).
Terne delle grandezze
0
½0 ½ = ¿0 ¿
0
Tensioni di linea
½ Z½ = ¿
Correnti di linea
¿
Tensioni di fase o stellate
½ ½=¿ ¿
Componenti simmetriche
½áZ ½ = ‖]‖
áZž
∙ ½ Z ½ = ¿áZ| ¿
áZu
½ℐ ½ = ‖]‖
ℐž
∙ ½0 ½ = ¿ℐ| ¿
ℐã
½á ½ = ‖]‖
áž
∙ ½ ½ = ¿á| ¿
áu
Figura 45
Nel particolare caso di sistemi simmetrici ed equilibrati, è ovvio che le componenti omopolare ed inversa di tutte le
terne di grandezze sono identicamente nulle e che, quindi, ogni terna si identifica con la propria componete simmetrica
di sequenza diretta
Pertanto nei sistemi simmetrici ed equilibrati si ha:
½áZ ½ = ¶
Sistemi Trifase
0
0
¶
0
½ℐ ½ = ¶0 ¶
0
0
½á ½ = ¶ ¶
0
Pagina 59 di 69
Nel caso più generale, dei sistemi dissimmetrici e squilibrati a quattro conduttori, salvo la componente omopolare delle
tensioni di linea (terna sempre pura), che è sempre identicamente nulla FáZž = 0G, tutte le terne di grandezze sono
rappresentate dalle componenti simmetriche di tutte e tre le sequenze:
0
½áZ ½ = ¿áZ| ¿
áZu
áž
½á ½ = ¿á| ¿
áu
ℐž
½ℐ ½ = ¿ℐ| ¿
ℐã
Relazione fra le componenti simmetriche
Per determinare adesso le relazioni fra le componenti simmetriche delle tensioni di un sistema trifase qualsiasi e le
componenti simmetriche delle correnti, riprendiamo in esame il sistema dissimmetrico e squilibrato a quattro conduttori
con accoppiamento induttivo fra le fasi (figura 46)
Figura 46
Nella relazione generale:
“ ‖ ∙ ‖0 ‖
‖ ‖ = ‖1
1̅
“‖ = ¿1̅
‖1
1̅
dove
1̅
1̅
1̅
1̅
1̅ ¿
1̅
che lega i valori delle tensioni ai valori delle correnti, sostituiamo alle matrici delle tensioni e delle correnti, le loro
espressioni in funzione delle rispettive componenti simmetriche:
“‖ ∙ ‖S‖ ∙ ½ℐ ½
‖S‖ ∙ ½á ½ = ‖1
Premoltiplichiamo i due membri dell’uguaglianza ottenuta, per la matrice inversa delle sequenze:
‖S‖
∙ ‖S‖ ∙ ½á ½ = ‖S‖
“‖ ∙ ‖S‖ ∙ ½ℐ ½
∙ ‖1
Ricordando allora che il prodotto di una matrice per la sua inversa è uguale alla matrice unità (il cui prodotto per una
qualunque matrice dà, per risultato, la matrice stessa) e che, però, il prodotto fra matrici non gode della proprietà
commutativa, si ottiene la relazione:
½á ½ = ‖S‖
“‖ ∙ ‖S‖ ∙ ½ℐ ½
∙ ‖1
che rappresenta il legame tra le componenti simmetriche delle tensioni e quelle delle correnti.
Sistemi Trifase
Pagina 60 di 69
Impedenze di sequenza
Effettuiamo ora il prodotto delle tre matrici ‖S‖
‖S‖
“‖ ∙ ‖S‖ =
∙ ‖1
91̅
1
= ¿91̅
3
91̅
L91̅
1
= ¿L91̅
3
L91̅
L91̅
L91̅
L91̅
L91̅
L91̅
L91̅
1 1
¶1
3
1
1
l
l
1̅
1
l ¶ ∙ ¿1̅
l
1̅
91̅
+ 1̅ + 1̅ ;
+ l1̅ + l 1̅ ; 91̅
+ l 1̅ + l1̅ ; 91̅
1̅
1̅
1̅
“‖ ∙ ‖S‖, otteniamo:
∙ ‖1
1̅
1
1̅ ¿ ∙ ¶1
1
1̅
91̅
+ 1̅ + 1̅ ;
+ l1̅ + l 1̅ ; 91̅
+ l 1̅ + l1̅ ; 91̅
1
l
l
1
l¶
l
+ 1̅ + 1̅ ;
1
+ l1̅ + l 1̅ ;¿ ∙ ¶1
+ l 1̅ + l1̅ ; 1
+ 1̅
+ l 1̅
+ l 1̅
+ 1̅ ; + 91̅ + 1̅ + 1̅ ; + 9 1̅ + 1̅ + 1̅ ;M
+ l 1̅ ; + 91̅ + l 1̅ + l 1̅ ; + 9l 1̅ + l 1̅ + 1̅ ;M
+ l 1̅ ; + 91̅ + l 1̅ + l 1̅ ; + 9l 1̅ + l 1̅ + 1̅ ;M
+ l 1̅
+ l 1̅
+ 1̅
+ l 1̅ ; + 9l 1̅ + l 1̅
+ l 1̅ ; + 9l 1̅ + 1̅
+ 1̅ ; + 9l 1̅ + l 1̅
+ l 1̅
+ 1̅
+ l 1̅
+ l 1̅ ; + 9l 1̅ + l 1̅
+ 1̅ ; + 9l 1̅ + l 1̅
+ l 1̅ ; + 9l 1̅ + 1̅
+ 1̅ ; + 9 1̅
+ l 1̅ ; + 9l 1̅
+ l 1̅ ; + 9l 1̅
+ 1̅ ; + 9 1̅
+ l 1̅ ; + 9l 1̅
+ l 1̅ ; + 9l 1̅
+ l 1̅
+ l 1̅
+ 1̅
+ l 1̅
+ 1̅
+ l 1̅
1
l
l
1
l¶=
l
+ l1̅ ;M
+ l1̅ ;M
+ l1̅ ;M
̅
å««
+ l 1̅ ;M
̅
+ l 1̅ ;M¿ = ¿å|«
̅
̅
;M
+l 1
åu«
̅
å«|
̅
å||
̅
åu|
̅
å«u
̅ ¿
å|u
åuu̅
Si ottiene quindi una matrice quadrata in cui i nove elementi si dicono impedenze di sequenza del sistema e la matrice:
̅
å««
̅
‖åv̅ ‖ = ¿å|«
̅
åu«
si chiama matrice delle impedenze di sequenza.
̅
å«|
̅
å||
̅
åu|
̅
å«u
̅
å|u ¿
åuu̅
̅ , å||
̅ , åuu̅ ; sono denominati autoimpedenze di sequenza; gli
Gli elementi della diagonale principale di tale matrice 9å««
̅
̅
̅
̅
̅
̅
altri 9å«| , å|ž , åžu , åuž , å|u , åu| ; sono detti mutue impedenze di sequenza.
Avremo quindi:
1
L91̅
3
1
̅ = L91̅
å|«
3
1
̅
åu« = L91̅
3
1
̅
å«| = L91̅
3
1
̅ = L91̅
å||
3
1
̅ = L91̅
åu|
3
1
̅ = L91̅
åžu
3
1
̅ = L91̅
å|u
3
1
åuu̅ = L91̅
3
̅ =
å««
Sistemi Trifase
+ 1̅
+ 1̅ ; + 91̅
+ l1̅
+ l 1̅
+ l 1̅ ; + 91̅
+ l 1̅
+ 1̅
+ 1̅ ; + 91̅
+ l1̅
+ l1̅ ; + 9l 1̅
+ l 1̅
+ l 1̅ ; + 9l1̅
+ l1̅ ; + 9l1̅
+ 1̅ ; + 9l1̅
+ l1̅
+ 1̅
+ l1̅
+ 1̅ ;M
+ l1̅ ; + 9l 1̅
+ l 1̅
+ l1̅
+ 1̅ ; + 91̅
+ l 1̅
+ l1̅ ; + 9l 1̅
+ 1̅
+ l 1̅ ; + 9l1̅
+ l 1̅
+ 1̅
+ 1̅
+ l 1̅ ; + 9l1̅
+ l 1̅
+ l 1̅ ; + 9l 1̅
+ l 1̅
+ 1̅
+ l1̅ ; + 91̅
+ 1̅ ; + 9l 1̅
+ l1̅
+ l1̅
+ 1̅
+ 1̅ ; + 9 1̅
+ l 1̅ ; + 9l1̅
+ l1̅ ; + 9l 1̅
+ l1̅
+ l1̅
+ 1̅
+ l 1̅
+ 1̅ ;M
+ 1̅ ;M
+ l1̅ ;M
+ l1̅ ;M
+ l1̅ ;M
+ l 1̅ ;M
+ l 1̅ ;M
+ l 1̅ ;M
Pagina 61 di 69
Nel caso particolare dei carichi senza accoppiamento mutuo fra le fasi (1̅ = 1̅ = 1̅ = 1̅ = 1̅ = 1̅ = 0;, le
tre autoimpedenze di sequenza risultano uguali tra di loro e le sei mutue impedenze di sequenza risultano uguali a tre a
tre.
Infatti, dalla matrice prima ricavata, si deduce che nel caso particolare dei carichi con fasi indipendenti la matrice delle
impedenze di sequenza risulta:
da cui
dove si è posto 1̅
91̅
1
‖åv̅ ‖ = ¿91̅
3
91̅
= 1̅ , 1̅
91̅
+ 1̅ + 1̅ ;
+ l1̅ + l 1̅ ; 91̅
+ l 1̅ + l1̅ ; 91̅
+ l 1̅ + l1̅ ; 91̅
91̅
+ 1̅ + 1̅ ;
̅
̅
+ l1 + l 1 ; 91̅
+ l1̅ + l 1̅ ;
+ l 1̅ + l1̅ ;¿
+ 1̅ + 1̅ ;
1
̅ = å||
̅ = åuu̅ = 91̅ + 1̅ + 1̅ ;
Ñå««
3
Ï
1
̅ = å|ž
̅ = åu|
̅ = 91̅ + l1̅ + l 1̅ ;
å«u
3
Ð
1
Ï ̅
̅
̅
91̅ + l 1̅ + l1̅ ;
Îå«| = å|u = åuž = 3
= 1̅ e 1̅
= 1̅ .
Come può rilevarsi osservando le precedenti espressioni, i valori delle auto e mutue impedenze di sequenza
corrispondono, nel caso particolare in esame, al risultato che si otterrebbe applicando le formule di scomposizione in
componenti simmetriche, alla terna di numeri complessi, 1̅ , 1̅ , 1̅ , rappresentativi delle impedenze delle fasi del
carico. Per tale motivo, i tre valori ai quali si riducono le impedenze di sequenza per i carichi con le fasi indipendenti, si
dicono le componenti simmetriche del carico.
1
Ñæ̅ž∗ = 91̅ + 1̅ + 1̅ ;
3
Ï
1
æ̅|∗ = 91̅ + l1̅ + l 1̅ ;
3
Ð
Ï ∗ 1 ̅
91 + l 1̅ + l1̅ ;
Îæ̅u = 3
Nel caso infine dei carichi con fasi indipendenti ed equilibrati 91̅ = 1̅ = 1̅ = 1̅; le precedenti componenti
simmetriche diretta ed inversa sono nulle; quindi le nove impedenze di sequenza si riducono alla sola componente
omopolare
æ̅ž∗ = 1̅
Legge di Ohm mediante le componenti di sequenza
In virtù di quanto detto, la legge di Ohm relativa ad un sistema trifase qualsiasi, può esprimersi, in funzione delle
componenti simmetriche, nella forma:
Che corrisponde al sistema:
Sistemi Trifase
½á ½ = ‖åv̅ ‖ ∙ ½ℐ ½
̅ ℐž + å«|
̅ ℐ| + å«u
̅ ℐã
áž = å««
̅ ℐ| + å|u
̅ ℐã
̅ ℐž + å||
Üá| = å|«
̅ ℐž + åu|
̅ ℐ| + åuu̅ ℐã
áu = åu«
Pagina 62 di 69
Come è facile rilevare dalle equazioni precedenti, i nove valori delle auto e mutue impedenze, che costituiscono gli
elementi della matrice, possono essere determinati sperimentalmente con semplici misure, inviando successivamente
nel sistema una terna diretta di correnti ℐ|∗ , poi una terna inversa ℐu∗ , infine una terna omopolare ℐž∗ e misurando ogni
volta le tensioni.
Indicando con
∗
∗
ážž
, á|ž
e áuž∗ le componenti simmetriche delle tensioni misurate quando il sistema è percorso dalla sola terna
di correnti di sequenza omopolareℐž∗ ;
∗
∗
∗
b) áž|
, á||
e áu|
le componenti simmetriche delle tensioni misurate quando il sistema è percorso dalla sola terna
di correnti di sequenza omopolare ℐ|∗ ;
∗
e áuu∗ le componenti simmetriche delle tensioni misurate quando il sistema è percorso dalla sola terna di
c) ážu∗ , á|u
correnti di sequenza omopolare ℐu∗
a)
dal sistema scritto prima:
̅ ℐž∗ + å«|
̅ ℐ|∗ + å«u
̅ ℐu∗
áž = å««
∗
∗
̅ ℐž + å||
̅ ℐ| + å|u
̅ ℐu∗
á| = å|«
̅ ℐž∗ + åu|
̅ ℐ|∗ + åuu̅ ℐu∗
áu = åu«
abbiamo che le nove impedenze di sequenza del sistema sono:
a)
∗
̅ ℐž∗
ážž
= å««
∗
̅ ℐž∗
á|ž = å|«
̅ ℐž∗
áuž∗ = åu«
∗
̅ ℐ|∗
áž|
= å«|
∗
̅ ℐ|∗
b) á|| = å||
∗
̅ ℐ|∗
áu|
= å|u
c)
Il sistema già scritto in precedenza:
ážu∗
∗
á|u
áuu∗
=
=
=
̅ ℐu∗
åu«
̅ ℐu∗
åu|
åuu̅ ℐu∗
̅ = áÞÞ
å««
∗
∗
da cui
ℐÞ
̅ = áßÞ
å|«
∗
∗
ℐÞ
̅ = áçÞ∗
åu«
∗
ℐÞ
da cui
da cui
̅ = áÞß
å«|
∗
̅ =
å||
̅ =
å|u
∗
ℐß
∗
áßß
∗
ℐß
∗
áçß
∗
ℐß
̅ = áÞç∗
åu«
∗
ℐç
̅ = áßç
åu|
∗
∗
ℐç
á
åuu̅ = çç∗
̅ ℐž + å«|
̅ ℐ| + å«u
̅ ℐã
áž = å««
̅ ℐž + å||
̅ ℐ| + å|u
̅ ℐã
Üá| = å|«
̅
̅
̅
áu = åu« ℐž + åu| ℐ| + åuu ℐã
∗
ℐç
Evidenzia che, ciascuna componente simmetrica delle tensioni è determinata contemporaneamente da tutte e tre le
componenti simmetriche delle correnti.
Sistemi Trifase
Pagina 63 di 69
Nel caso particolare di carichi con fasi indipendenti, ricordando sia:
sia
1
̅ = å||
̅ = åuu̅ = 91̅ + 1̅ + 1̅ ;
Ñå««
3
Ï
1
̅ = å|ž
̅ = åu|
̅ = 91̅ + l1̅ + l 1̅ ;
å«u
3
Ð
1
Ï ̅
̅
̅
91̅ + l 1̅ + l1̅ ;
Îå«| = å|u = åuž = 3
1
91̅ + 1̅ + 1̅ ;
3
1
æ̅|∗ = 91̅ + l1̅ + l 1̅ ;
3
1
∗
æ̅u = 91̅ + l 1̅ + l1̅ ;
3
æ̅ž∗ =
le precedenti equazioni, espresse in funzione delle componenti simmetriche del carico, divengono:
̅ ℐ| + å«u
̅ ℐã = æ̅ž∗ ℐž + æ̅u∗ ℐ| + æ̅|∗ ℐã
̅ ℐž + å«|
áž = å««
̅ ℐ| + å|u
̅ ℐã = æ̅|∗ ℐž + æ̅ž∗ ℐ| + æ̅u∗ ℐã
̅ ℐž + å||
Üá| = å|«
̅ ℐž + åu|
̅ ℐ| + åuu̅ ℐã = æ̅u∗ ℐž + æ̅|∗ ℐ| + æ̅ž∗ ℐã
áu = åu«
Infine, per i carichi con fasi indipendenti ed equilibrati, indicando con 1̅ il valore comune delle impedenze delle fasi, la
legge di Ohm assume la forma:
½á ½ = 1̅ ∙ ½ℐ ½
Perciò se sono alimentati da una terna dissimmetrica di tensioni, si ha:
áž = 1̅ ℐž
Üá| = 1̅ℐ|
áu = 1̅ ℐã
Vale a dire nei carichi equilibrati ogni componente simmetrica della terna delle tensioni è determinata solo dalla
corrispondente componente simmetrica della terna delle correnti.
Principi di Kirchhoff mediante le componenti di sequenza
Anche i principi di Kirchhoff, applicati ai sistemi trifase, possono essere espressi mediante semplici relazioni, in
funzione delle componenti simmetriche delle terne di grandezze.
Riprendiamo le relazioni:
Æ F½
Ä
Æ ½0 9Ä; ½ = 0
9Ä;
Ä
½ − ½1̅9Ä; ½½0 9Ä; ½G = 0
Dalla prima, ricordando che ½0 9Ä; ½ = ‖]‖ ∙ ½ℐ 9Ä; ½, si ha:
Æ ‖]‖ ∙ ½ℐ 9Ä; ½ = 0
Ä
da cui
Æ ½ℐ 9Ä; ½ = 0
Ä
Sistemi Trifase
Pagina 64 di 69
Dalla seconda ricordando che ½
9Ä;
½ = ‖]‖ ∙ ½á 9Ä; ½ e che ‖åv̅ ‖ = ‖]‖
∙ ½1̅ 9Ä; ½ otteniamo:
Æ F‖]‖ ∙ ½á 9Ä; ½ − ½1̅ 9Ä; ½ ∙ ‖]‖ ∙ ½ℐ 9Ä; ½G = 0
Ä
Æ ‖]‖F½á 9Ä; ½ − ‖]‖
Ä
∙ ½1̅9Ä; ½ ∙ ½ℐ 9Ä; ½G = 0
Æ ‖]‖F½á 9Ä; ½ − ‖åv̅ ‖ ∙ ‖]‖ ∙ ½ℐ 9Ä; ½G = 0
Ä
da cui:
Æ F½á 9Ä; ½ − ‖åv̅ ‖ ∙ ‖]‖ ∙ ½ℐ 9Ä; ½G = 0
Ä
In definitiva abbiamo ottenuto:
Æ F½á
Ä
9Ä;
Æ ½ℐ 9Ä; ½ = 0
Ä
½ − ‖åv̅ ‖ ∙ ‖]‖ ∙ ½ℐ 9Ä; ½G = 0
Circuito equivalente di sequenza
Confrontando ora le relazioni che legano le tensioni alle correnti di un sistema trifase qualsiasi con quelle che
intercorrono fra le rispettive componenti simmetriche
Ü
̅ ℐž + å«|
̅ ℐ| + å«u
̅ ℐã
áž = å««
̅ ℐž + å||
̅ ℐ| + å|u
̅ ℐã
Üá| = å|«
̅
̅
̅
áu = åu« ℐž + åu| ℐ| + åuu ℐã
= 1̅ 0 + 1̅ 0 + 1̅ 0
= 1̅ 0 + 1̅ 0 + 1̅ 0
= 1̅ 0 + 1̅ 0 + 1̅ 0
Si rileva che hanno una forma perfettamente analoga e le seconde possono essere dedotte dalle prime, sostituendo alle
terne delle tensioni e delle correnti, le terne dei vettori base delle rispettive componenti simmetriche ed alle auto e
mutue impedenze, rispettivamente, le auto e mutue impedenze di sequenza.
Figura 47
Tale analogia formale consente, ai fini del calcolo, di poter sostituire al circuito reale un circuito ideale equivalente,
come quello di figura 47, che si chiama circuito equivalente di sequenza.
Sistemi Trifase
Pagina 65 di 69
Sistemi fisicamente simmetrici
Si dicono sistemi fisicamente simmetrici, i sistemi trifase nei quali:
le autoimpedenze sono uguali tra loro 1̅ = 1̅ = 1̅ = 1̅ ;
̅ ;
le mutue impedenze ascendenti sono uguali tra loro 1̅ = 1̅ = 1̅ = 1è{
̅
le mutue impedenze discendenti sono uguali tra loro 1̅ = 1̅ = 1̅ = 1è|
Effettuando il calcolo delle impedenze di sequenza (cfr. pag. 51) si rileva che nei sistemi fisicamente simmetrici tutte le
mutue impedenze di sequenza sono nulle e le autoimpedenze di sequenza sono:
̅ = 1̅ + 1è{
̅ + 1è|
̅ = å«̅
å««
̅ = 1̅ + l 1è{
̅ + l1è|
̅ = å|̅
Ýå||
̅
̅
̅
̅
åuu = 1 + l1è{ + l 1è| = åu̅
Di conseguenza la matrice delle impedenze di sequenza diventa una matrice diagonale:
å«̅
‖åv̅ ‖ = ¿ 0
0
0
å|̅
0
0
0¿
åu̅
E le relazioni fra le componenti simmetriche delle tensioni e delle correnti assumono la forma:
áž = å«̅ ℐž
Üá| = å|̅ ℐ|
áu = åu̅ ℐã
Queste relazioni evidenziano che, diversamente da quanto visto per i sistemi dissimmetrici, nei sistemi fisicamente
simmetrici, ciascuna componente simmetrica della terna delle tensioni è determinata solo dalla corrispondente
componente simmetrica della terna delle correnti e viceversa.
E’ chiaro quindi che nel caso di sistemi fisicamente simmetrici, in virtù del principio di sovrapposizione degli effetti, il
circuito equivalente di sequenza può essere suddiviso in tre circuiti monofasi equivalenti, in ciascuno dei quali ogni
componente simmetrica di tensione agisce sulla corrispondente autoimpedenza di sequenza, generando la omonima
componente simmetrica di corrente (figura 48).
Figura 48
Questi circuiti si dicono circuiti monofasi equivalenti di sequenza.
Sistemi Trifase
Pagina 66 di 69
Potenze trifasi mediante le componenti di sequenza
Dall’espressione della potenza complessa:
|]̅| = ‖ ‖ ∙ ‖0Ç‖ = |
Ricordando inoltre che:
‖] ̅ ‖
e che
Ñ
Ï
Abbiamo:
]̅ =
∙ 0_ +
= áž + á| + áu
∙ 0_ +
∙ 0_ |
Ö_ž
∙ ½o_½ = ¿ Ö_u ¿
Ö_|
= áž + l á| + láu
Ð
Ï
Î = áž + lá| + l áu
∙ 0_ +
∙ 0_ +
Ñ
Ï
0_ = ℐ_ž + ℐ_u + ℐ_|
0_ = ℐ_ž + l ℐ_u + lℐ_|
Ð
Ï
Î0_ = ℐ_ž + lℐ_u + l ℐ_|
∙ 0_ =
= Fáž + á| + áu GFℐ_ž + ℐ_u + ℐ_| G + Fáž + l á| + láu GFℐ_ž + l ℐ_u + lℐ_| G + Fáž + lá| + l áu GFℐ_ž + lℐ_u + l ℐ_| G
= áž Fℐ_ž + ℐ_u + ℐ_| + ℐ_ž + l ℐ_u + lℐ_| + ℐ_ž + lℐ_u + l ℐ_| G +
á| Fℐ_ž + ℐ_u + ℐ_| + l ℐ_ž + l < ℐ_u + l ℐ_| + lℐ_ž + l ℐ_u + l ℐ_| G +
áu Fℐ_ž + ℐ_u + ℐ_| + lℐ_ž + l ℐ_u + l ℐ_| + l ℐ_ž + l ℐ_u + l < ℐ_| G
e notando che:
otteniamo:
l = l« = 1
l< = l
]̅ = áž Fℐ_ž + ℐ_u + ℐ_| + ℐ_ž + l ℐ_u + lℐ_| + ℐ_ž + lℐ_u + l ℐ_| G +
á| Fℐ_ž + ℐ_u + ℐ_| + l ℐ_ž + lℐ_u + ℐ_| + lℐ_ž + l ℐ_u + ℐ_| G +
áu Fℐ_ž + ℐ_u + ℐ_| + lℐ_ž + ℐ_u + l ℐ_| + l ℐ_ž + ℐ_u + lℐ_| G =
= áž Â3ℐ_ž + Fℐ_u + lℐ_u + l ℐ_u G + Fℐ_| + lℐ_| + l ℐ_| GÃ +
á| ÂFℐ_ž + lℐ_ž + l ℐ_ž G + Fℐ_u + lℐ_u +l ℐ_u G + 3ℐ_| Ã
áu ÂFℐ_ž + lℐ_ž +l ℐ_ž G + 3ℐ_u + Fℐ_| + lℐ_| + l ℐ_| GÃ
Ricordando inoltre che:
Si ottiene
Sistemi Trifase
Fo_ + lo_ + l o_G = 0
]̅ = 3Fáž ℐ_ž + á| ℐ_| + áu ℐ_u G
Pagina 67 di 69
Separando poi la parte reale da quella immaginaria di ]̅ ed indicando con :ž , :| , :u gli angoli di fase dei vettori base
delle componenti simmetriche delle tensioni rispetto ai vettori base delle corrispondenti componenti simmetriche delle
correnti, si ricavano le espressioni delle potenze attiva e reattiva del sistema:
Cioè:
?
?
?ç ;
=
]̅ = 3Fáž ℐ_ž + á| ℐ_| + áu ℐ_u G = 39áž ℐž Þ + á| ℐ| ß + áu ℐu
= 3L9áž ℐž cos :ž + á| ℐ| cos :| + áu ℐu cos :u ; + 9áž ℐž sin :ž + á| ℐ| sin :| + áu ℐu sin :u ;M = X + Y
X = 39áž ℐž cos :ž + á| ℐ| cos :| + áu ℐu cos :u ; =
= 3Fáž ∙ ℐž + á| ∙ ℐ| + áu ∙ ℐu G =
= 3½á ½ ∙ ½ℐ ½
Y = 39áž ℐž sin :ž + á| ℐ| sin :| + áu ℐu sin :u ; =
= 3Fáž ∧ ℐž + á| ∧ ℐ| + áu ∧ ℐu G =
= 3½á ½ ∧ ½ℐ ½
Da queste espressioni si deduce che la potenza attiva e quella reattiva sono determinate dalle sole combinazioni fra le
componenti simmetriche omonime delle tensioni e delle correnti.
Nel caso di sistemi a tre conduttori essendo ℐž = 0, si ha:
X = 3Fá| ∙ ℐ| + áu ∙ ℐu G
Y = 3Fá| ∧ ℐ| + áu ∧ ℐu G
Quindi le potenze attiva e reattiva sono determinate dalle solo componenti diretta ed inversa delle tensioni e delle
correnti, cioè, come già rilevato, dipendono dalle sole tensioni di linea e sono indipendenti dal centro stella prescelto.
Sistemi Trifase
Pagina 68 di 69
Sommario
Sistemi trifase
1
1
Generalità .............................................................................................................................................................. 1
1.1
Sistemi simmetrici di tensioni
2
1.2
Sistemi equilibrati di correnti
4
2
Sistemi simmetrici ed equilibrati ........................................................................................................................... 6
2.1
Potenza nei sistemi simmetrici ed equilibrati
10
2.2
Misura della potenza nei sistemi simmetrici ed equilibrati
12
2.3
Campo magnetico rotante di Galileo Ferraris
16
3
Sistemi dissimmetrici e squilibrati....................................................................................................................... 19
3.1
Tensioni e correnti nei sistemi trifase a tre fili
20
3.2
I centri stella nei sistemi trifase dissimmetrici e squilibrati
22
3.3
Potenza nei sistemi dissimmetrici e squilibrati
26
3.4
Teorema di Aron
27
3.5
Misura della potenza nel sistema dissimmetrico e squilibrato
29
4
Rifasamento nei sistemi trifase ............................................................................................................................ 31
5
Convenienza dell’utilizzo dei sistemi trifase ....................................................................................................... 33
6
Accoppiamenti mutui nei sistemi trifase ............................................................................................................. 34
7
Studio generale dei sistemi trifase ....................................................................................................................... 44
7.1
Rappresentazione matriciale delle grandezze trifase
44
7.2
L’algebra delle sequenze
50
7.3
Scomposizione di un sistema trifase di grandezze
53
7.4
Analisi dei sistemi trifase mediante le componenti simmetriche
59
Sommario
Sistemi Trifase
69
Pagina 69 di 69