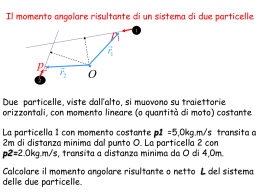
103
Torna all’indice
Interazioni radiazione materia
Introduzione
I termini "radiazione" e "particella" richiedono un chiarimento. Per "radiazione" intendiamo energia
elettromagnetica che si propaga nello spazio, ma con riferimento a quell'intervallo di frequenze più
alte dello spettro visibile; tipicamente dai raggi X in poi. Il campo del visibile, delle microonde,
dell'infrarosso e delle radiofrequenze è escluso. Quindi, per i nostri scopi, la radiazione può essere
descritta da un flusso di quanti, i fotoni, con energia E = hν ed impulso p = hν/c, essendo ν la
frequenza della radiazione. Questi quanti interagiscono con le cariche elettriche con una probabilità
che è dell'ordine dell'interazione tra due cariche.
Il termine "particella" comprende tutte quelle entità composte di materia (energia) alle quali possono
essere assegnate proprietà classiche discrete e quantistiche come la massa a riposo m0, lo spin s, la
carica q, la vita media τ, ecc.. L'uso del termine particella non è sempre chiaro: parliamo di molecola
di idrogeno, mentre quando ci riferiamo al nucleo dell'atomo di idrogeno, il protone, lo chiamiamo
particella. L'elettrone, il neutrone, il neutrino, il mesone π, ecc. sono dette particelle; ugualmente
però usiamo lo stesso termine per i frammenti di fissione, per i nuclei di elio (particelle α), e per gli
ioni pesanti. Possiamo visualizzare allora una particella, in generale, come un punto massivo che
descrive una certa traiettoria sotto l'influenza di forze esterne e di certe condizioni iniziali. Questo è
un "modello" molto utile per i nostri scopi e in molti calcoli.
Le interazioni tra le particelle sono regolate da quattro forze fondamentali: quella elettromagnetica,
l’interazione debole, l’interazione forte e la gravitazionale. Alle diverse interazioni è possibile
associare delle costanti di accoppiamento, adimensionali, che ci danno una misura della "forza" con
cui l'interazione agisce. In base al valore di questa costante abbiamo la seguente tabella:
g0 = 0.1 ÷ 0.15
Interazione forte
Riguarda le forze nucleari tra protoni e neutroni, per esempio.
Interazione elettromagnetica
g0 = α = 1/137 (e2/ h c)
Avviene tra particelle cariche.
g0 = 10-5
Interazione debole
Un esempio è il decadimento β.(n → p + e- +
(G M2p)
f
νe )
Interazione gravitazionale
g0 = 10-39
Questo valore è stato ricavato dalla forza tra due protoni.
Le particelle interagenti con la materia possono, a loro volta essere divise in due classi: particelle
cariche e neutre. Appartengono alle particelle cariche il protone, α, k, π, µ, elettrone e positrone,
ecc; mentre in quelle neutre rientrano il neutrone, γ, ecc.
In realtà ai fini dell'interazione con la materia gli elettroni si comportano in modo assai "simile" ad
un γ piuttosto che alle altre particelle cariche, mentre il neutrone si comporta in modo diverso da
tutte le altre.
104
Interazione di particelle cariche
Cerchiamo di dare una descrizione generale "unificata" di tutti i processi coinvolti. L'approccio, date
le finalità sperimentali del corso è, ovviamente, semi classico. Vedremo come quasi tutto ciò che
interessa l'interazione dei carichi con la materia possa essere derivato dalla Diffusione coulombiana
singola.
L'interazione delle particelle cariche e dei fotoni con la materia è essenzialmente di tipo
elettromagnetico. Essa conduce ad una riduzione dell'energia della particella entrante nel materiale
(con la variazione della sua direzione) o nell'assorbimento del fotone. Le particelle accoppiate con il
campo nucleare ( interazione forte), come i protoni, i neutroni, i mesoni π, i nuclei, sono soggetti a
interazione nucleare che però ha una distanza di interazione (range) molto minore di quella relativa
all'interazione e.m.. Quindi l'interazione nucleare diventa importante solo quando la particella ha
sufficiente energia da superare la barriera coulombiana dovuta alla carica elettrica del nucleo e
quando lo spessore di materiale attraversato è sufficientemente grande da essere confrontabile con il
libero cammino medio nucleare (∼ 60 g/cm2) che per il 208Pb con densità ρ ∼ 12 g/cm3 dà 5 cm. Le
particelle pesanti (p, π, µ) perdono energia essenzialmente attraverso urti (elettromagnetici) con gli
elettroni atomici del materiale, mentre per gli elettroni la perdita avviene sia attraverso collisioni con
gli elettroni del mezzo sia per irraggiamento (bremsstrahlung) dovuto alla variazione della traiettoria
provocata dal campo elettrico del nucleo. I fotoni invece, danno luogo all’effetto fotoelettrico
interagendo con gli elettroni legati degli atomi del mezzo, all’effetto compton quando collidono con
gli elettroni quasi liberi delle shell atomiche più esterne e, a più alta energia ( > 1 MeV ),
interagiscono col campo elettrico del nucleo creando coppie elettrone-positrone.
Alcune definizioni importanti
Sezione d'urto
Consideriamo un flusso di particelle (o radiazione) che investe un singolo centro di diffusione. Allora
definiamo sezione d'urto σ per diffusione (scattering) da una singola particella (centro di
diffusione), il rapporto:
σ=
flusso diffuso
flusso incidente per unità di area
allora σ ha le dimensioni di una superficie e può essere immaginata come l'area del centro di
diffusione proiettata sul piano normale alla direzione del flusso incidente. Se ora indichiamo con n la
densità dei centri diffondenti (particelle/cm3 o nuclei/cm3), in uno spessore dx di materiale vi
saranno ndx centri per unità di area. Quindi la probabilità, dp, che si abbia un'interazione nello
spessore dx sarà:
I
σ
flusso diffuso
dp = s =
quindi: dp =
I 0 flusso incidente
I0 S
⋅ Sndx = σndx
I0
dalla quale si deduce che la probabilità di avere una collisione è proporzionale a ndx cioè al numero
di centri diffusori per unità di superficie.
Allora la sezione d'urto σ è quel fattore che trasforma la proporzionalità in uguaglianza.
Le sezioni d'urto atomiche e nucleari σAt.Nuc. sono dell'ordine di 10-24 cm2 (barn), valore non
sorprendente se si considera che la sezione geometrica di un nucleo di raggio r pari a circa 1 fm è:
σ Geo = π r 2 = 3.14 10 -26 A 2/3 cm 2
105
Sezione d'urto differenziale
Per un singolo centro diffusore definiamo:
dσ (θ , ϕ ) flusso diffuso nell' elemento dΩ a θ e ϕ
=
dΩ
flusso incidente per unità di superficie
Ne segue che:
2π
π dσ
σ = ∫ dϕ ∫
d (cos θ )
0
0 dΩ
se dopo la diffusione le particelle hanno energie diverse ossia possono avere una varietà di energie
possibili, allora definiamo:
2
d σ (θ , ϕ ) flusso con energia tra E ed E + dE diffuso nell' elemento dΩ a θ e ϕ
=
dΩdE
flusso incidente per unità di superficie
ne segue che:
dσ (θ , ϕ ) ∞ d 2σ (θ , ϕ , E )
= ∫
dE
dΩ
dΩdE
0
in cui l'integrazione è estesa a tutte le energie del flusso diffuso.
Coefficiente di assorbimento
Consideriamo un flusso di particelle per unità di area
I0, incidente su un materiale di spessore t. Se
indichiamo con I(x) il flusso presente alla distanza x
dalla superficie di impatto nel materiale allora la
"variazione" del flusso alla quota x, -dI(x), per aver
attraversato lo spessore infinitesimo dx a causa del
processo di diffusione, sarà data dal prodotto del flusso
stesso per la probabilità dp di avere avuto una diffusione
nel tratto infinitesimo dx. Porremo quindi: -dI(x) = dp I(x) ma essendo dp = σndx si ha : -dI(x) =
−σnx
I(x)σndx, per cui si avrà, integrando: I ( x) = I 0e
(Si è posto la costante d'integrazione uguale
al valore iniziale dell'intensità, cioè I(0) = I0.)
L'equazione ottenuta rappresenta il flusso che sopravvive dopo lo spessore x, o semplicemente il
flusso alla quota x di materiale attraversato. Si può facilmente ricavare il seguente rapporto:
I ( x)
= e −σnx che rappresenta la probabilità di sopravvivenza dei componenti del flusso incidente
I0
alla generica quota x e quindi, la probabilità di diffusione in tutto lo spessore t, sarà:
p(t) = 1- probabilità di sopravvivenza in t
cioè: p(t ) = 1 − e
−nσt
che è la probabilità di diffusione in t.
La grandezza fisica: n⋅σ = k [L-3 L2 =L-1] è detta coefficiente di assorbimento, mentre il suo
inverso:
1
=λ
nσ
[ L] è detto cammino libero medio o lunghezza di assorbimento.
La densità dei centri diffusori, n, si può scrivere nel seguente modo:
n=ρ
N0
A
se i centri di diffusione sono i nuclei
106
ne = ρ
N0
Z se i centri di diffusione sono gli elettroni
A
essendo: N0 il numero di Avogadro; ρ la densità ; A il numero di massa; Z il numero atomico del
materiale.
Si vede quindi che le due grandezze fisiche introdotte, k e λ, dipendono sia dal tipo di processo,
attraverso la σ, sia dal materiale, tramite n. E' spesso utile esprimere lo spessore di materiale,
anziché in centimetri, come " massa equivalente attraversata " ossia in g/cm2, così avremo lo
spessore:
dξ[ g/cm2 ] = ρ[g/cm3]dx[cm]
Il coefficiente di assorbimento, k, è spesso espresso anch'esso in termini " massivi " e si introduce
allora il " coefficiente di assorbimento di massa ":
k
µ=
ρ
e quindi la probabilità di " sopravvivenza " o la frazione di
 cm -1
cm 2 
I
=


= e −µξ
flusso non assorbita si può riscrivere:
3
g

I0
 g cm
Diffusione Coulombiana Singola da Nuclei
Limiti per un approccio classico
Assumiamo che il nucleo non si muova apprezzabilmente in seguito al passaggio della particella di
carica ze, rmassa m e velocità v, allora l'impulso trasferito dalla particella al nucleo dovuto al campo
elettrico E della particella passante è:
+∞
+∞
+∞
dt
Ze +∞
∆p = ∫ F⊥ (t )dt = Ze ∫ E⊥dt = Ze ∫ E⊥ ( )dt =
∫ E⊥dx
dx
v −∞
−∞
−∞
−∞
D'altronde, applicando il teorema di Gauss al cilindro che ha per asse la traiettoria della particella si
ha:
+∞
r
4πze = ∫ E ⋅ dS = ∫ E ⊥ 2πbdx
−∞
da cui:
+∞
2 ze
∫ E ⊥ dx =
b
−∞
e, l'impulso trasferito:
Ze +∞
2Zze 2
∆p =
∫ E ⊥ dx =
v −∞
bv
Si è considerato solo E⊥ in quanto la componente parallela alla traiettoria si annulla, per simmetria,
da -∞ a +∞.
Questa descrizione è significativa dal punto di vista del principio di indeterminazione, se l'incertezza
con cui conosciamo la posizione della particella, ∆b, è minore di b. Cioè:
se ∆b < b → ∆b/b < 1 approccio classico
D'altronde dal principio di indeterminazione sappiamo che: ∆b⋅∆p ∼ h per cui ∆b ≅
h
<b
∆p
107
Sostituendo il ∆p trovato abbiamo:
hbv
2Zze 2
<b
ovvero
hβc
2Zze 2
<1
Zze 2
>≈ 1
quindi la condizione per un approccio classico del processo è:
hβc
Vediamo con i numeri. La costante di struttura fine α è:
2
−38
α=
2.6 ⋅10
1
e
≈
≅
4πε 0 hc (12.56) 2 ⋅10 −12 ⋅ 10 −34 ⋅ 3 ⋅ 10 8 137
allora la condizione per un approccio classico sarà:
Zz  e 2  Zz
Zz
= α >1 ⇒
> 137


β  hc  β
β
per una particella con z = 1 ( non così rare visto che stiamo parlando di µ, e, p,..) sarà:
Ricordando che ET = mγ con γ =
1
1− β
2
Z
> 137 .
β
risulta che per nuclei leggeri e medi (Z =1 ÷ 40), β
deve essere compreso tra 0.1 e 0.01.
Diffusione Coulombiana Singola
Questo processo può essere schematizzato come un urto elastico di una particella di carica ze e
massa M con un nucleo di carica Ze e massa m. Abbiamo già visto
r i limiti di validità dell'approccio
classico e abbiamo calcolato l'impulso ∆p che il campo E , dovuto alla particella incidente,
trasferisce alla particella bersaglio.
Consideriamo il caso in cui il bersaglio è costituito da un nucleo e calcoliamo la sezione d'urto
differenziale del processo di diffusione.
Osserviamo che la traiettoria della particella è
un'iperbole e che il nucleo è nel fuoco interno se
la forza è attrattiva (ze < 0), è invece esterno se
la forza è repulsiva (ze > 0)
Caso di forza repulsiva
Volendo calcolare la sezione d'urto differenziale
di questo processo possiamo procedere nel
seguente modo.
La dσ, vista come elemento di superficie è:
2πbdb. All'angolo θ, nell'angolo
solido elementare dΩ = 2πsinθdθ
si ha:
dσ
2πbdb
bdb
=
=
. Bisogna perciò cercare
dΩ 2πsinθdθ sinθdθ
db
b
con b parametro d'urto.
dθ
108
L'impulso trasferito al nucleo era: ∆p = 2
zZe 2
bv
Ma, a causa dell'urto, la particella incidente con impulso p, subisce una variazione nel suo impulso.
Dall'analisi
della
figura
ricaviamo,
nell'ipotesi
che
pi
≈
pf
≈
p
∆p 2 = p i2 + p 2f − 2 p i p f cos θ
(impulso trasferito al nucleo trascurabile)
∆p 2 = 4 p 2 sin 2 θ2
Con facili sostituzioni otteniamo:
θ
zZe 2
1
db zZe 2 cos 2
b=
⋅
⇒
=
pcβ sin θ
dθ 2 pβc sin 2 θ
2
2
2
dσ  zZe 2 
1
=
e quindi
⋅
dΩ  pβc  4 sin 4 θ
2
dalla quale si vede la maggiore probabilità per le piccole deviazioni. La particella nell'attraversare il
mezzo subisce molte deviazioni di piccola entità.
Questo ci costringerà a trattare il caso di diffusione coulombiana multipla. Mettendo le opportune
unità di misura la sezione d'urto si può anche scrivere nel seguente modo:
2 2
dσ
dΩ µ = 0
= 5.19
[
z Z
]
⋅
1
(mb ster )
p ( Mev ) ⋅ β sin 4 θ
s =0
c
2
i deponenti s,µ stanno ad indicare che questa formula è valida per particelle con spin e momento
magnetico nulli. Per valori diversi di s, µ esistono dei fattori correttivi applicati soprattutto a energie
relativistiche
dσó
dσ ó
=
⋅F
dΩÙ ì µ ≠ 0
dΩÙ s = 0
µ =0
s ≠0
Vediamo alcuni valori di F.*
SPIN
0
1
2
0
1
1
2
≥1
1
1
1
* vedi
µ
W. Pauli Rev. Mod. Phys. 13,203
≥1
F
1
1 − β SIN 2
2
θ
2
(µ − 1)2 SIN 2 θ2
1+
β 4 SIN 2 θ 2
6(1 − β 2 )
4( N − 1) 2 SIN 2 θ 2
3(1 − β 2 )
109
Abbiamo già visto che una particella carica che attraversa un assorbitore subisce numerose diffusioni
angolo di uscita della particella dal materiale ma di
che sarà dato dalla radice quadrata
dell'angolo quadratico medio che si può esprimere attraverso la distribuzione di probabilità derivata
diffusione coulombiana.
P(θ θ è il numero di urti con deviazione compresa tra e θ θ.
∞
2
2
θ
= ∫ θ ⋅ P(θ )dθ
0
Il primo a trattare il problema quantitativamente fu E.J.Williams**
Costruiamo questa funzione partendo dalla diffusione singola, poiché è connessa con la causa della
deviazione.
2 2
dσ  zZe
=
dΩ  pβc

1
 ⋅
 4 sin 4 θ

2
Questa rappresenta la frazione di particelle del fascio incidente, diffusa nell'angolo solido elementare
dΩ all'angolo θ; o, in altri termini, la probabilità che una particella di carica ze ed impulso p venga
diffusa, in un singolo urto, nell'angolo solido elementare dΩ da un nucleo di carica Ze. Se il
materiale attraversato è costituito da No/A centri diffusori e se la particella attraversa lo spessore dx,
allora possiamo scrivere :
P(θ )dΩdx =
No
A
 dσ 
⋅
 ⋅ dΩdx
 dΩ  c
 n °at. cm 2
g 
⋅
⋅ ster. ⋅

2 
g
ster.
cm


che rappresenta la probabilità che la particella venga diffusa nell'angolo solido dΩ nell'attraversare
lo spessore dx e in cui No è il numero di Avogadro e A è il peso atomico del mezzo attraversato.
Poiché la maggior parte degli urti avviene con piccole deviazioni allora calcoliamo il < θ 2 > per
angoli piccoli. Quindi sinθ∼θ (approssimazione di molti urti con piccole deviazioni) ed otteniamo:
z 2 Z 2 e 4 N o dθ
P(θ )dθ = 8π
⋅
⋅
2
3
A
( pβc )
[
]
θ
per cui il < θ 2 > nell'attraversare lo spessore x g cm 2 diventa:
2
2

zZe
2

 No
θ
= 8π
 pβ c 


⋅
+∞
⋅ x ⋅ ln θ 0
A
Ci sarebbe una divergenza logaritmica per θ = 0 che può essere rimossa ponendo dei limiti fisici
ragionevoli su θ con il seguente ragionamento.
•
La
dσ
è stata calcolata per un nucleo puntiforme. Invece il nucleo atomico ha una
dΩ c
dimensione finita che, approssimativamente, si può esprimere come:
1
r
Rn = o ⋅ A 3 ∼ 1.4 10 13 A1/3 cm
2
** vedi
Proc. Roy. Soc. A169,531,(1939) ; Phys. Rev. 58,292 (1940)
110
in cui ro =
e2
4πε 0 mc
2
≈ 2.8 ⋅10 −13 cm è il raggio classico dell'elettrone e A1/3 deriva dal fatto
sperimentale che il volume di un nucleo atomico cresce proporzionalmente al numero di nucleoni A.
•
Quando la particella carica passa ad una distanza dal nucleo maggiore del raggio atomico
Ra ,"vede " la carica del nucleo schermata dagli elettroni orbitali, cioè ridotta. Dal modello statistico
di Thomas-Fermi dell'atomo si ottiene il seguente raggio atomico:
−1
r0
Ra ≈ 2 ⋅ Z 3
α
•
La meccanica ondulatoria ci insegna che ad ogni particella con impulso p è associata
un'onda la cui lunghezza è data dalla relazione di De Broglie: λ =
•
h
p
Nell'ipotesi che l'onda associata alla particella proiettile non sia apprezzabilmente perturbata
nell'avvicinarsi al nucleo, è possibile esprimere l'angolo θ di diffusione, corrispondente ad un
determinato parametro d'impatto r, come: θ = λ / r che, classicamente, rappresenta anche l'angolo
di diffrazione di un'onda di lunghezza λ che investe un oggetto di dimensioni lineari r.
E' chiaro quindi che i limiti entro cui ci dovremo aspettare sensibili variazioni di θ sono tra il raggio
nucleare Rn e il raggio atomico Ra confrontati con la lunghezza d'onda di De Broglie λ della
particella.
λ
= θ m e una massima deviazione per :
Ra
R
θ
λ
θ≈
= θ M . Da cui, è facile vedere che : M = a e si può allora scrivere :
Rn
θm
Rn
Avremo quindi una minima deviazione per : θ ≈
θ
avendo tenuto conto che
2




2
z 2 Z 2e 4 N o
= 8π
⋅
⋅ x ln 

2
1
A
( pβ c )

 2
α ( ZA) 3 
2
Ra
=
Rn α 2 ( zA) 13
L'argomento del logaritmo può essere trasformato nel seguente modo:
2
2
1
2 
1



6
1
1


6
−
−
1
2
2
(ZA)− 6  =  2 Z 1 Z 3  ≅ 193 Z  Z 3 
=
1

  A
α
α

A 6


α 2 ( ZA) 3


Abbiamo così :
< θ 2 >= 16π
  Z  16 − 1 
z 2 Z 2e4 N o
x
ln
193  Z 3 
⋅
⋅
( pβc ) 2 A
  A 

Tenendo conto che il rapporto Z/A varia, dai nuclei leggeri a quelli pesanti, nell'intervallo (1/2)
1
Z 6
≤Z/A≤1/(2.5), si può scrivere: 193 
≈ 183 e quindi:
 A
θ 2 = 16π

−1 
z 2Z 2e4 N o
⋅
⋅ x ln 183 ⋅ Z 3 
A
( pβ c ) 2


111
Spesso, per comodità, si è soliti introdurre la grandezza fisica lunghezza di radiazione Xo
(caratteristica del materiale):
[ ]

−1 
N
1
≅ 4α Z 2 ro2 ln 183 ⋅ Z 3  cm-1
Xo
A


per esprimere più semplicemente il < θ 2 > [1] :
θ 2 ≅ z2
E s2
x
⋅
 MeV  2 2 X o
⋅β c
p2 
 c 
[1]
1
 4π  2
E s =   ⋅ mc 2 ≅ 21.2 MeV .
α 
dove Es è una quantità costante che vale:
Si arriva infine ad una formula pratica per l'angolo medio di diffusione:
1
21.2
x
2 2
θ
≅z
 MeV 
⋅ βc
p
 c 
⋅
Xo
L'assunzione che la deviazione media è composta da un gran numero di diffusioni piccole, se
comparate con la media, conduce alla conclusione che, su un cammino di lunghezza finita, la
somma delle deflessioni ha una distribuzione gaussiana.
Per piccoli angoli di deflessione la
θ 2 , ora calcolata rappresenta una buona stima della reale
deflessione.
Per angoli grandi la deflessione è quella data dalla diffusione singola.
Assumiamo la seguente distribuzione Gaussiana (non proiettata):
2
− θ
2 θ2
2θ
W (θ )dθ =
θ
e
dθ
in cui < θ 2 > , dedotta in modo più accurato:
θ 
θ 2 = 2θ12 ln  1 
θm 
N Z ( Z + 1) 2 4
con θm ≅ λ/Ra (quello da noi calcolato) e θ 1 = 4π
z e x
A ( pβc ) 2
Il < θ 2 > è molto simile al precedente calcolato ed ha un preciso significato fisico.
Esso rappresenta l'angolo per il quale vi è, in media, una sola collisione con angolo θ > θ1. Risulta
quindi :
4


3


0
.
157
(
Z
+
1
)
Z
Z
x
θ2 =
⋅ z2
z 2 x ln 1.13 ⋅ 10 4 ⋅
2
2
A
A( pβc)
in cui il fattore 0.157 = 4π
1
Ne 4 [esu ]
2.56 ⋅10
−12
β 



[
e pβc [MeV] e x g cm 2
vedi B. Rossi-K. Greisen: Revs. Mod. Phy. 13,240 (1941)
]
112
L'espressione approssimata [1] funziona bene per spessori relativamente grandi e maggiori di
2 1
 137  3
2
2
x o = 6.7
 A g cm . Per piccoli spessori la [1] sovrastima < θ >
 Z 
[
]
Alcuni valori di xo:
110 g/cm2
Pb
xo =
C
xo = 8000 g/cm2
E' spesso utile considerare gli angoli θx, θy, cioè le proiezioni dell'angolo θ sul piano xy
perpendicolare alla direzione di volo della particella. La distribuzione di θx è ancora Gaussiana :
−
Px (θ x )dθ x =
1
1
2π θ 2  2
x 

e
θ x2
2 θ x2
dθ x
La distribuzione per θy ha la stessa forma di θx.
2
F (α ) F2 (α )


W (θ )2πdθ = 2e −α + 1
+
+ ....αdα
2
B
B


Ancora per piccoli spessori, ma in un intervallo di velocità della particella incidente intermedio tra
bassa (approccio classico) e relativistico, una trattazione più sofisticata è stata fatta da Moliere[2] che
dà una distribuzione del tipo :
in cui:
α=
θ
χ B
;
χ=
σ
 E + mc 2
mc 2  A

−
 mc 2
E + mc 2 

44.8Z
ed E rappresenta l'energia cinetica, σ = g/cm2 e B è una misura del numero medio di collisioni; le
funzioni F1 e F2 .. sono tabulate e per i valori esatti si rimanda alla referenza
Con questo calcolo si arriva ad un valore di < θ 2 > sotto radice pari a[3] :
1
 0.982 0.117

2 2 2
= χ B ⋅ 1 +
+
+ ...
θ
 
2
π 

B
B

Per una dettagliata esposizione sul singolo e multiplo scattering si può vedere: W.T.Scott. Rev. Mod.
Phy. 35,231 (1963).
Si veda Y. Goldschiidt -Clermond Nuovo Cimento 1,220 (1950)
2
3
Z.Naturforsch 3,78 (1948)
Siegbann "alfa,beta and gamma ray spectroscopy" North-Holland Publ.comp. (1965)
113
Perdita di Energia per Ionizzazione
Consideriamo ora lo stesso tipo di processo e.m. di diffusione coulombiana in cui il centro di
diffusione non è più il nucleo, ma gli elettroni degli orbitali atomici.
Sono naturali le seguenti considerazioni:
1. Essendo il processo formalmente identico possiamo usare la formula della sezione d'urto già
ricavata.
2. Occorre però apportare le seguenti modifiche dettate da considerazioni di carattere fisico:
•
La massa del centro di diffusione, Mbers, ossia l'elettrone, ora non è molto più grande della
massa della particella proiettile. Anzi ora Me è molto minore, a meno che il proiettile non sia un
elettrone. Quindi:
bers.
M
pro.
<< M
Allora l'energia cinetica trasferita nell'urto: E =
(∆p )2
2 M bers.
non è più trascurabile, l'urto è anelastico, e la particella proiettile, pur subendo una piccola
deviazione, perde notevole energia in ogni urto.
• Il numero di centri diffusori per unità di massa è diverso: ora non sono più No/A
[at./g] bensì NoZ/A [elettroni/g]. Sembrerebbe quindi esserci un fattore moltiplicativo Z nella
sezione d'urto, ma la carica del bersaglio è Z = 1 per cui la sezione d'urto è minore giusto di un
fattore Z. Questo significa che, dal punto di vista della diffusione multipla, la presenza degli elettroni
non giuoca, in genere, un ruolo importante tranne che nei materiali molto leggeri come quelli
idrogenati in cui Z del nucleo è uguale a 1.
Quindi una particella carica attraversando la materia, oltre a subire numerose piccole deflessioni
da parte del campo del nucleo, lascia parte della sua energia per urti con gli elettroni atomici.
Vogliamo ora calcolare l'energia media (si tratta ancora di un processo statistico) che una particella
di massa m, carica ze, impulso p, rilascia attraversando un mezzo di spessore dx. Questa energia
ceduta agli elettroni atomici provoca l'eccitazione e la ionizzazione degli atomi del mezzo lungo il
percorso della particella. La successiva diseccitazione degli atomi, nei tempi e nei modi che verranno
analizzati quando parleremo dei rivelatori a scintillazione, restituisce, in parte, sotto forma di fotoni
l'energia assorbita.
Dalla teoria della diffusione multipla avevamo dedotto, nel caso di piccole deflessioni (sinθ ∼ θ) la
funzione di distribuzione P(θ). Considerando ora Z = 1 ed il numero di centri per unità di massa
NoZ/A si ha:
P(θ )dθdx = 8π
z 2e4
( pβc )2
Z
N o dθ
dx
A θ3
La perdita di energia media dovuta agli urti anelastici per unità di percorso è, per definizione:
−
d E
= ∫θθM Eθ ⋅ P(θ )dθ
m
dx
essendo Eθ l'energia persa per singolo urto. Come abbiamo già detto la funzione di distribuzione
P(θ)dθ è facilmente ricavabile dall'osservazione che il processo coinvolto, responsabile della perdita
di energia, è simile alla diffusione coulombiana con la differenza che ora la particella passando
vicino all'elettrone oltre a subire una deflessione (in questo caso trascurabile in seguito alla piccola
114
massa dell'elettrone rispetto a quella del nucleo) trasferisce all'elettrone un impulso ∆p ≅ pθ[4] e
p 2θ 2
quindi una energia Eθ ≅
. La funzione di distribuzione assume la forma :
2m
P(θ )dθdx = 8π
z 2e4
( pβc )2
Z
N o dθ
dx
A θ3
e tenendo presente la Eθ si può allora scrivere ( dopo aver integrato):
d E
N
θ
4πz 2 e 4
Z o ln M
−
=
dx
A
θm
me β 2 c 2
ion
I limiti angolari di integrazione θm e θM si ricavano nel seguente modo.
•
In una descrizione classica del processo, la massima energia trasferita dalla particella di
′ =
massa M all'elettrone di massa me vale : E M
4m e M
(1 + me
M)
2
E con E energia cinetica della
p 2θ 2
particella incidente. Poiché, come abbiamo già visto, l'energia trasferita nell'urto è Eθ ≅
,
2m
2me
con facili passaggi[5] e sotto l'ipotesi M >> me si ricava: θ M =
M
•
Per θm occorre fare altre considerazioni. Se consideriamo un elettrone legato con frequenza
vibrazionale ν (essendo hν il potenziale di ionizzazione I) una collisione, per impartire energia
hν, cioè ionizzare gli atomi, deve avvenire in un tempo ∆t corto rispetto a T=1/ν. D'altronde il
tempo di collisione è τ ≅ r/vγ se r è il parametro d'urto, v la velocità della particella e γ il fattore
di Lorentz per tener conto della dilatazione del tempo della particella. Quindi il parametro
d'urto massimo rM, o classicamente, l'estensione dell'oggetto che diffrange l'onda di lunghezza
λ, si avrà nel caso limite quando τ ≈ T :
rM 1
=
vγ ν
e quindi θm : θ m =
;
rM =
vγ
ν
θ
λ
hν
mv 2 γ
. Quindi il rapporto tra gli angoli diventa: M = 2
=
rM
pvγ
θm
hν e l'energia
d E
media persa per unità di percorso è: −
dx
=
ion
4πz 2 e 4
me β 2 c 2
Z
in cui hν è il potenziale di ionizzazione dell'atomo del materiale.
realtà ∆p = 2psin(θ/2) ma poiché sinθ ∼θ allora ∆p ∼2pθ/2 ∼pθ
2
2
5 E ′ ≅ 4 m e E ≅ 4 me p = 2 p m e che va eguagliato a E
M
θ
M
M 2M
M2
4In
N o  2m e v 2γ
ln
A  hv





115
Alcune osservazioni:
1.
Il termine hν al denominatore del logaritmo rappresenta il potenziale di ionizzazione
dell'atomo del materiale. Ovviamente esso va sostituito con un valore medio I = <hν> calcolato su
tutti i livelli atomici. Alcuni valori sono:
Elemento
<hν>
[eV]
4
63.4±0.5
Be
13
Al
Cu
166.5±1
375.6±20
48
Ag
585.0±40
79
Au
1037±100
29
2.
Questa formula è stata dedotta nel caso di piccole deflessioni della particella incidente
(M >> me) quindi è valida solo per particelle pesanti (heavy particles). Per gli elettroni il termine
logaritmico deve essere sensibilmente modificato. Infatti gli elettroni perdono energia essenzialmente
attraverso collisioni con il campo elettrico del nucleo emettendo radiazione e.m. Questo processo è
detto " Bremmsstrahlung ".
3. Per energie basse (zona B-C nella figura) l'andamento delle perdite varia molto rapidamente con
la velocità della particella v a causa della diminuzione del tempo di collisione e quindi
dell'energia trasferita. La sua espressione può essere scritta come:
d E
z2
m
∝
= z2
2
dx
2E
v
essendo m la massa della particella ed E la sua energia cinetica.
Questa relazione è molto utile in quanto permette (quando è applicabile) di identificare la particella
dalla misurazione della dE/dx e della E.
d E
E
4.
dx
∝ z 2m
Per energie cinetiche ancora minori ( E ~ 400 KeV), cioè:
E = ET − m
; γ =
ET
E
= +1
m
m
;
E
= γ − 1 ≤ 0.1
m
le perdite variano come 1/v.
5.
Per energie cinetiche bassissime ( E < 25 KeV), (tratto A-B della figura) quando il tempo
d'urto τ > T = 1/ν, l'energia trasferita diminuisce quasi linearmente con v.
−
d E
dx
∝v
116
6.
Nella regione relativistica (v ~ c) zona C-E della curva, il fattore 1/v2 diventa costante e il
comportamento dipende dall'argomento del logaritmo. Risulta quindi un aumento di dE/dx con
l'energia. Si viene cosi a determinare un punto di minimo nella curva ( punto C) per valori di β ~
0.96. Si parla di particelle al minimo di ionizzazione ( MIP).
7.
Quando invece l'energia della particella è molto alta, oltre la zona relativistica [γ >> 1]
interviene il cosiddetto effetto densità o screening.
Quando il parametro d'urto è maggiore di un raggio atomico, la particella esperimenta anche i campi
dovuti agli altri atomi vicini. Ne risulta un indebolimento del campo effettivo " visto " dalla
particella e quindi una minore perdita di energia. Poiché, come si può ricavare, la probabilità di
avere grandi parametri d'urto è maggiore alle alte energie, lo screening interviene in tale regione.
8.
Se espressa in termini di E/m = γ-1 la funzione d<E>/dx è una curva universale (per carica
unitaria). Diversamente se messa in funzione dell'energia cinetica, occorre scalare per il rapporto
delle masse ( vedi figura rapporto π/p)
−
d E
dx
∝ z2
m
1
≡ z2
2E
2(γ − 1)
9.
Per quanto riguarda la dipendenza dal materiale, se si esprime lo spessore, come abbiamo
fatto, in g/cm2, la dipendenza è:
N
d<E>

−
= f (β , I ) ⋅ z 2  o Z 
dx
A


cioè dipende da Z/A che è maggiore nei nuclei leggeri piuttosto che in quelli pesanti
anche se la variazione è piccola.
Se invece la esprimiamo in centimetri abbiamo:
−
e varia molto più rapidamente.
N

= f ( β , I ) ⋅ z 2  o Zρ 
dx[cm]
 A

d E
1
Z 1
≤ ≤
2.5 A 2
117
Una funzione di distribuzione molto utile è P(E)dE poiché ci dà la probabilità che avvenga un urto
con perdita di energia compresa tra E ed E+dE. La si può facilmente ricavare dalla P(θ)dθ
ricordando l'energia trasferita in un urto dalla particella all'elettrone ed esprimendo la θ = θ(E)
2 2
E=
p θ
2m
con semplici sostituzioni si ricava
P( E )dE = W
dE
E2
in cui
W=
2πz 2 Ze 4 N o
0.15 Z 2
x≅
z x in [MeV]; con x [g/cm2]
2 2 A
2 A
mβ c
β
L'energia media persa si ricava allora :
E = ∫ EE M EP( E )dE = W ln ( E M Em )
m
2
E
θ
e tenendo conto che M = M si vede la congruenza di <E> con -d<E>/dx.
2
Em θ m
Fluttuazioni nelle Perdite di Energia Ionizzante
Le perdite di energia per ionizzazione sono soggette ad apprezzabili fluttuazioni a causa della natura
statistica del processo di ionizzazione. Quindi nel progettare un esperimento occorre conoscere
l'ammontare di tali fluttuazioni per sapere la massima precisione ottenibile dall'apparato. Vi sono
due possibili casi:
1.
Durante l'attraversamento la particella subisce un gran numero di collisioni con il massimo
trasferimento di energia E nel singolo urto e l'energia totale persa è composta da tante piccole perdite
di energia. In questo caso le fluttuazioni sono regolate dalla statistica Gaussiana.
2.
La particella ha una bassa probabilità di trasferire la massima energia e, l'energia totale E
persa, è minore di Emax quindi ci sono non molte collisioni e, di conseguenza, le fluttuazioni sono
grandi. Questo caso è applicabile a particelle relativistiche per quasi tutti gli spessori e a particelle
non relativistiche per piccoli spessori. In questo caso le fluttuazioni sono regolate dalla distribuzione
di Landau.
Determiniamo le condizioni per le due statistiche.
Dalla P(E)dE si ricava
P(E > Emax ) = ∫E∞ W
max
dE
E2
=
W
Emax
che rappresenta la probabilità di avere una collisione con trasferimento di energia Emax o il numero
di urti con E > Emax.
Quindi le condizioni sono :
W/Emax >>1
Gauss
W/Emax <<1
Landau
considerando che :
E max = 2
che diventa :
(E + Mc
)
+ mc 2 ⋅ mc 2
− 2 mc 2
M 2 c 4 + m 2 c 4 + 2mc 2 E + Mc 2
2
(
)
118
E max ≈
2β 2
⋅ mc 2
1− β 2
β4
e ponendo
(1 − β 2 ) << 0.074t
Z 1
≅
si ricava :
A 2
Gauss
β4
(1 − β 2 ) >> 0.074t
Landau
che stabiliscono in quale modo fluttua il processo di ionizzazione in base al β della particella e allo
spessore t [in g/cm2] di materiale attraversato
Esempi.
Gauss
Un protone non relativistico β ≅ 1/3 (Ep ≅ 50 MeV) che attraversa x = 1 g/cm2 ha
β4
≅ 0.013 e quindi segue la statistica di Gauss.
1− β 2
Landau
Un mesone µ con En = 1 GeV che attraversa x = 10 g/cm2 ha
β4
≅ 100 e quindi segue la
1− β 2
statistica di Landau.
Fluttuazioni gaussiane
La deviazione standard percentuale è:
1
 Eeff .  2
σ

= 

E
E


dove Eeff . =
Emax
E

ln  max 
 Em 
e rappresenta l'energia effettiva persa per ogni urto. Quindi : N=<E>/Eeff
numero di collisioni e poiché si sa che per una statistica gaussiana
rappresenta l'effettivo
1
σ
=
si vede che,
N
N
effettivamente, le fluttuazioni vanno come l'inverso della radice quadrata del numero di collisioni.
Ricordando che :
E
m2v 4
ln max = ln
2
2
Em
hv
(1 − β )
si ha che per Z = 26 e β = 1/3 ) ln(Emax/Em) = 15 (Nel modello di Fermi-Thomas, in un sistema
con i atomi , si può scrivere , per cui al denominatore del secondo membro al posto di <hv> va ZI
con I costante quindi l'energia effettiva persa per urto è Eeff . ≈
EM
.
15
Per
g/cm2
un
protone
da
Ep
=
50
MeV
,
x
=
1
di
scintillatore
4m
E
E p ≅ 110 KeV per
cui: E eff ≅ M ≅ 7 KeV .
M
15
0.15 Z 2
E
W=
⋅ z x ≅ 675 KeV si avrà: E (per grammo) = Wln M ≅ 10 MeV
Em
β2 A
Emax =
si
ha:
Poiché:
119
E
Essendo il numero di collisioni pari a: N =
Eeff
≅
10
7 ⋅ 10 − 3
≅ 1400
si ottiene una deviazione standard percentuale
1
σ
=
≅ 3%
N (1400) 12
Fluttuazioni di Landau
In questo caso gli urti con grosso rilascio di energia sono poco probabili quindi <E> va calcolato
integrando
solo
fino
a
circa
4
 4W 
dE
4W

W E ≅ ∫ E WE
= W ln 
m
E2
 E min 
si può ricavare che la deviazione standard percentuale
è:
σ
2W
≈
che è indipendente dal materiale e dallo
E
E
spessore.
Questa è una tipica distribuzione di Landau per un
protone di Ep = 3 GeV. Si può calcolare una
σ
≈ 20%
E
Relazione Range-Energia
Con questo termine (range) si intende il cammino che è necessario, ad una particella di energia Eo,
entrando in un materiale, per perdere tutta la sua energia per ionizzazione. Abbiamo quindi:
R  dE 
E0 = ∫ 
dx
0  dx 
Si definisce R range della particella in quel materiale. Poiché:
−
N

= f (β , I ) ⋅ z 2  o Z 
dx
 A 
d E
allora:
dE
dx = −
N

z 2  0 Z  f (β )
 A 
e quindi:
0
R
R = ∫ dx = − ∫
0
dE
E0 z 2  N 0 Z  f (β )
 A

=
E0 dE
1
∫
f (β )
N 
z2 0 Z  0
 A 
e poiché :
E=
allora: dE = m⋅ g(β)dβ e, quindi:
1
mβ 2 c 2
2
; dE = mc 2 βdβ
120
R=
β0 ( )
g β
m
dβ
∫
2  N0  0 f ( β )
Z
z 
 A 
dalla quale si deduce che il range, a parità di β, è:
• inversamente proporzionale alla carica al quadrato della particella.
• proporzionale alla massa della particella
• inversamente proporzionale alla densità elettronica: NoZ/A
dE
.
dx ion
Possiamo dedurre il valore del range dalla
Infatti detta: f(E) = dE/dx allora dx = dE/[f(E)].
Integrando quindi si ha:
dE
R( E ) = − ∫E0
0 (− dE dx )
Allora definiamo R(E) range della particella in quel materiale.
Poiché a basse energie si ha:
−
dE
1
∝
dx ion E
risulta: R ( E ) ∝ E 02 con Eo= energia della particella incidente.
• Questo è valido fino ad energie cinetiche E ∼ mo. Oltre questo valore, in zona relativistica,
poiché le perdite diventano pressoché costanti, allora f(E) = cost. e quindi:
E0
R = ∫ dE ∝ E0
0
cioè cresce quasi in modo lineare con l'energia iniziale.
• Per valori di energia più alti la relazione è del tipo E = kRn
ma a causa delle grandi
dE
non è possibile dare una formulazione esatta teoricamente e
fluttuazioni già viste nella
dx ion
ci si affida così a formule pratiche del tipo:
( )
(
)
R p E p = 1.0072 Rα 3.971E p − 0.20 [cm ]
valida per protoni con 4 ≤ Ep ≤ 15 MeV oppure a:
3
R ≈ (0.005E + 0.285) ⋅ E 2
•
Inoltre si può far uso della seguente considerazione: Poiché'
4 2
dE
4πθ z
∝
dx ion
mV 2
NZ si ha che dr=
M
m
1
V 3 dV
(
Z 2 4ðe 4 N o Z ln 2mV 2 I
)
dove I e' il potenziale medio di ionizzazione; quindi, per uno stesso mezzo assorbitore, noto il range
per una particella, si può' dedurre quello di qualsiasi altra (pesante).
• Per energie maggiori di 15 MeV, il range per protoni può essere calcolato dalla formula
empirica:
1.8
 Ep 

R p = 100

 9.3 
•
Bragg-Kleeman hanno proposto la seguente relazione per il range di una particella in mezzi
diversi:
121
r1 ρ 0
=
r0 ρ1
A1
A0
in cui ρ,A sono rispettivamente la densità e il numero atomico.
In un composto si ha:
A=
n1 A1 + n 2 A2 + n3 A3 + .....
n1 A1 + n 2 A2 + n3 A3 + ...
in cui n1,n2,n3,....sono le frazioni atomiche dei costituenti di peso atomico A1, A2,
Per l'aria si ha :
A0 = 3.82 ; ρ 0 = 1.226 ⋅10−3 gr/cm 3
r = 3.2 ⋅10 −4
@ 15 °C e 760 mmHg per cui si ha
A
r (aria) = K ⋅ r (aria)
ρ
Ecco alcuni valori tipici per scintillatori più usati
ρ [g/cm3]
K [10-4]
3.04
1.25
7.79
C14 H 12
2.98
1.16
8.21
NaI
CsI
ZnS
9.34
11.4
7.07
3.67
4.51
4.10
8.14
8.09
5.52
Scintillatore
formula
A
Antracene
C14 H 10
trans-Stibilene
NaI
CsI
ZnS
122
Range per elettroni
L'elettrone, nell'attraversare la materia, perde energia oltre che per eccitazione e ionizzazione,
anche per radiazione. Quest'ultimo termine interviene ad energie piuttosto alte (relativamente). Per
esempio un elettrone nel Pb ha una energia critica Ec pari a:
m
≈ 9.7 MeV [Pb ]
Z
E c ≈ 100 MeV [aria ]
E c = 1600
A causa della sua piccola massa l'elettrone, nell'attraversare un mezzo, subisce numerose deflessioni
che lo costringono a fare un percorso molto tortuoso. Il cammino totale è circa 1.2 ÷ 4 volte la
spessore attraversato. Quindi il concetto di range è diverso per particelle altamente ionizzanti e per
elettroni. Per le prime esso coincide con lo spessore attraversato, per gli elettroni invece, esso
corrisponde al cammino necessario per fermarlo.
Per estrapolare il grafico si può usare la formula : r mg cm 2 = 530E [MeV ] − 106
[
]
Katz-Penfold,1952
•
Per gli elettroni il range espresso in g/cm2 è praticamente indipendente dal mezzo
attraversato.
Katz-Penfold hanno dato la seguente espressione per il range pratico R p
•
se 0.01 ≤ E0 ≤ 2.5 MeV
R p = 412 E 0n
[mg cm ]
2
n = 1.265 − 0.954 ln E 0
•
se 2.5 ≤ E0 ≤ 20 Me
R p = 530E 0 − 106
[mg cm ]
2
Fluttuazione nel range
A causa delle fluttuazioni di
è di tipo gaussiano:
dE
anche il R ha delle fluttuazioni considerevoli. La distribuzione
dx ion
123
−
1
P( R)dR =
α π
e
(R − R0 )2
α2
dR
che rappresenta la probabilità di una particella di definita energia iniziale, di avere un R compreso
tra R e R+dR con :
α 2= 2(R − R0 )2Av = 2∫ P( R)(R − R0 )2dR
e con
R0 = ∫E0
0
dE
dE dx
Range medio
2
Una espressione per (R − R0 )Av è stata ottenuta da Bohr per particelle con velocità iniziale molto
alta. L'espressione è la seguente:
−3
N E0  dE 
Z∫ 
 dE
A 0  dx 
2
In pratica è difficile ottenere il valore (R − R0 )Av e quindi si preferisce ottenere la curva che
esprime il numero di particelle sopravvissute in funzione dello spessore di materiale attraversato:
N
Si trova che la curva vale N = 0 per R=R0 .
2
Inoltre, in questo punto, la curva ha la sua
massima pendenza pari a −α π . Conducendo la
tangente a questo punto si ottiene il cosiddetto
Range estrapolato Rext.
(R − R0 )2Av
= 4πe 4
con Rext . = R0 +
1
2α π
La differenza Rext - Ro
è il cosiddetto parametro di Straggling, S, definito
nel seguente modo:
S2 =
π
(R − R0 )2Av
2
Con questo parametro si avrà quindi una distribuzione della seguente forma:
π
−
(R − R0 )2
1
2
4S
P( R)dR =
2S
e
dR
Esempio:
protoni in aria: 100 S/Ro è Ro= 5 cm ; 2.13 per Ro= 10 cm ; 1.78 per Ro=100 cm Il rapporto S/Ro
varia poco con Z.
124
Interazione dei γ con la materia
I fotoni perdono energia o sono assorbiti nella materia fondamentalmente a causa di tre processi:
1. Effetto fotoelettrico, predominante a basse energie 0 < hν < 150 KeV
2. Effetto Compton, dominante ad energie intermedie hν < qualche MeV
3. Produzione di coppie e+e-, prevalente ad alte energie: hν> 2 me ( soglia)
Poiché, come vedremo, tutti questi processi possono essere espressi in funzione della sezione d'urto
di diffusione Thomson, determineremo questa in modo classico ma completo per poi derivare
tutte le altre.
Sezione d'urto Thomson
Si tratta dell'interazione tra un'onda elettromagnetica (fotone) e un elettrone. Il processo Thomson
riguarda l'intervallo di energie dell'onda e.m. corrispondenti a lunghezze d'onda λ molto maggiori
del raggio classico dell'elettrone ro [ λ >> ro]. Ad esempio, prendiamo un fotone di energia E = hν
= 100 KeV, che rappresenta un'energia tipica della shell K per materiali con grande numero di
massa A. Ciò corrisponde ad avere:
c = λυëí
per cui: hc ≈ 200 MeV ⋅ fm ossia:
λ=
; E=
hc
λë
; ë λ=
hc
E
1200
[fm ] = 12000 fm ; ro ≈ 2.8 ⋅10 −13 cm ≈ 2.8 fm
0.1
quindi fotoni da 100 KeV hanno λ >> ro. Fino ad energie dell'ordine del MeV o, se vogliamo avere
un limite di carattere fisico, fino a E = hν ∼ mec2, la trattazione classica della diffusione Thomson
non mostra rilevanti deviazioni dall'osservazione. Inoltre occorrerà tener conto, nell'interazione con
l'elettrone, della natura ondulatoria dell'onda e.m. e si tratterà il processo come effetto Compton:
Lo schema che dobbiamo tener presente quindi nel descrivere la diffusione Thomson è quello di
un'onda e.m. piana polarizzata (è meglio supporla polarizzata per poi ricavare la sezione d'urto
differenziale non polarizzata) linearmente che investe un elettrone, inizialmente fermo nell'origine
di un sistema di coordinate. L'onda e.m. incidente lungo la direzione z con pulsazione ω è:
r
E = E 0 e i ( kz −ωt )
mette in oscillazione la carica elettrica( elettrone) secondo la direzione di polarizzazione del campo
r
E , sul piano z = 0.
La sezione d'urto si può esprimere come rapporto tra:
potenza irradiata per unità di dΩ
dσ
=
dΩ potenza incidente per unità di superficie
La potenza irradiata da una carica in moto, nel caso non relativistico, per unità di angolo solido dΩ,
con accelerazione v& è
dW
1 e2 2 2
=
⋅ v& sin Θ
dΩ 4π c 3
125
o
an
Pi
ne
io
s
ffu
di
di
z
P
punto di osservazione
k
θ
n
Θ
n1
y
φ
piano di polarizzazione
ε
x
r
dove Θ è l'angolo tra la direzione di osservazione (versore n$ ) e il vettore campo elettrico E .
L'equazione del moto della carica è:
2
2
r
2 e E
&
&
v =
mv = - E e
⇒
2
m
L'accelerazione impartita alla carica, mediata sul periodo T, è classicamente uguale a quello di
oscillazione della carica, e quindi:
2
e 2 E 02 1 T
e 2 E0
2
< v& 2 >=
ω
t
dt
=
cos
∫
m2 2
m2 T 0
perciò la potenza media irradiata per unità di angolo solido è:
dW
1 e4
=
E02 sin 2 Θ
dΩ
8π 2 3
m c
La potenza incidente per unità di superficie è quella trasportata da un campo e.m. ed è espressa dal
r
vettore di Pointing S
r
r
r r
r r
c r r
c r
c
c 2
S=
E^ B =
E ^ (nˆ1 ^ E ) =
nˆ1 ⋅ ( E ⋅ E ) − E ( E ⋅ nˆ1 ) =
E nˆ1
4π
4π
4π
4π
Il cui modulo è:
r
c 2
S =
E
4π
ed il valore medio:
S =
c 2
E0
8π
Quindi la sezione d'urto differenziale sarà:
dσ
dW
=
dÙ
dΩ
1
1 e4
8π
e4
2
2
E0 sin Θ
=
sin 2 Θ
r =
2
3
2
2
4
S 8π m c
cE0 m c
ossia:
dσ
= r02 sin 2 Θ
dΩ pol.
126
ove il suffisso pol. sta per polarizzata e r0 è il raggio classico dell'elettrone r0 ∼ 2.8 10-13 cm. Per
ricavare la sezione d'urto differenziale non polarizzata è conveniente esprimere l'angolo Θ in
funzione degli angoli θ, ϕ rispetto al piano di diffusione e di vibrazione della carica, si ha:
r
nˆ ⋅ v&
cos Θ = r = (sinθ ,0, cos θ ) ⋅ (cos ϕ , sinϕ ,0) = sinθ cos ϕ
v&
e quindi
(
dσ
= r02 1 − sin 2θ cos 2 ϕ
dΩ pol.
)
poiché: sin2Θ = 1-cos2Θ = 1-sin2θcos2ϕ.
Se l'onda elettromagnetica incidente non è polarizzata occorre mediare in ϕ (angolo sul piano di
polarizzazione). Si ottiene quindi:
r2
r2
dσ
= 0 ∫02π 1 − sin 2θ cos 2 ϕ dϕ = 0 1 + cos 2 θ
(Video-Clip)
dΩ n. pol 2π
2
Integrando[6] sull'angolo solido, otteniamo la sezione d'urto totale :
(
)
(
)
8
σ T = πr02 ≅ 66 ⋅ 10 −26 cm 2 ≅ 0.665 barn
3
che è la ben nota sezione d'urto totale Thomson.(Video-Clip)
Diffusione Compton
Come abbiamo già accennato, l'effetto Compton ha la stessa natura di quello Thomson,
rappresentando una sua estensione per energie più alte là dove non è più possibile considerare
l'interazione tra campo e.m. ed elettrone soltanto come un'interazione onda-corpuscolo, bensì come
una vera e propria interazione puntuale tra due particelle: il fotone e l'elettrone. In questo senso la
frequenza e quindi l'energia del fotone diffuso non sarà più la stessa del fotone incidente come
avveniva per l'urto Thomson. E' quindi naturale aspettarsi che:
1. La sezione d'urto compton sia una correzione
"relativistica" di quella Thomson
2. Il limite classico della sezione d'urto compton
e
γ
coincida con quella Thomson
Il processo di diffusione Thomson e anche la sua
versione per alte energie, Compton, può essere
schematizzato come in figura:
γ
Studiamo ora la cinematica del processo.
Per semplicità utilizzeremo i quadrivettori in modo
da scrivere una sola equazione per la conservazione
dell'energia e dell'impulso. Si ha: kµ+pµ = k'µ+p'µ
con µ = 1, .., 4
6σ
(
)
r02
dσ
2
dΩ =
∫ 1 + cos θ dΩ =
τ =∫
dΩ
2
2π −1
r02 

2
∫ dΩ − ∫ dϕ ∫ cos θd (cos θ )
2 
0
1

127
Le prime tre componenti sono spaziali e la quarta, temporale, è l'energia. Consideriamo l'urto
unidimensionale allora il quadrimpulso dell'elettrone, preso fermo nell'origine, è: pµ ≡ ( 0, 0, 0,
imc)
Analogamente si avrà per il fotone:
kµ ≡ ( 0, k, 0, ik)
quadrimpulso del fotone iniziale
k'µ ≡ ( 0, k'cosθ1, k'sinθ1, ik')
quadrimpulso del fotone finale
Ricaviamo p'µ , quadrimpulso dell'elettrone finale: p'µ = kµ+pµ -k'µ
Quadrando si ha:
pµ′ p′µ = pµ pµ + kµk µ + kµ′ k′µ + 2 pµk µ − 2 pµk′µ − 2kµk′µ
− m2c2 = −m2c2 + 0 + 0 + 2 pµk µ − 2 pµk′µ − 2kµk′µ
ossia:
p µ (k µ − k µ′ ) − k µ k µ′ = 0
− kmc + k ′mc − kk ′ cosθ1 + kk ′ = 0
Risolvendo per k' si ha l'impulso del fotone uscente:
k
k′ =
1+
k
(1 − cos θ1 )
mc
Per θ1 = π/2 si ha l'impulso trasverso trasferito all'elettrone:
′ =
k⊥
k
1 + k mc
Abbiamo ora due casi, dal punto di vista energetico:
1. k << mc
(bassa energia)
In tale situazione risulta k′ ≅ k quindi l'impulso trasferito ∆k dal fotone all'elettrone è piccolo ed il
fotone incidente e l'elettrone di rinculo, poiché il loro impulso è dello stesso ordine di grandezza,
sono localizzati essenzialmente nello stessa regione di spazio. Infatti il principio di indeterminazione
ci dice che:
∆x ≈
h
k
∆x ′ ≈
(fotone)
h
k′
(elettrone) ⇒ se k= k' ne segue ∆x ∼ ∆x'
Siamo in condizioni classiche e quindi vale ancora la sezione d'urto di Thomson.
2. k >> mc
(alta energia)
Ora risulta k′ ≅ mc quindi l'impulso trasferito è dell'ordine di mc per cui l'elettrone di rinculo è
h
h
h
ed essendo k >> mc risulta
<<
cioè il fotone incidente
mc
k
mc
risulta localizzato in un raggio molto minore di quello dell'elettrone. Questo determina un
abbassamento della sezione d'urto nel passaggio dal caso classico, Thomson, al caso relativistico, di
mc 2
un fattore proporzionale al rapporto tra gli impulsi. Quindi σ c ≈ σ T
.
localizzato in un raggio r ≈
hν
Quella esatta calcolata da Klein-Nishima, con considerazioni quantistiche e relativistiche, è:
σ kN
mc 2
= πr
hν
2
0
  2hν  1 
ln 2  + 2 
  mc 

128
Effetto Fotoelettrico
Parliamo di effetto fotoelettrico quando un fotone è completamente assorbito e tutta la sua energia è
trasferita ad un elettrone atomico. Quindi il fotone deve avere sufficiente energia da eccitare
l'elettrone legato dal suo stato quantico ad uno di energia maggiore o nel continuo (ionizzazione).
L'energia di legame delle shell più interne è:
K
E k ≈ Ry(Z − 1) 2 dove Ry= 13.5 eV.
Le altre shell vanno come:
L
M
EL
Z − 5) 2
(
≈
4
(Z − 13)
EM ≈
19
L'andamento medio della σ in funzione di hν va come (hν)-3. Per energie lontane dal K-shell e in un
range non relativistico (hν<<mc2) si ha7:
7
2 2

mc 
σ ph. = σ T 4 2 Z 5α 4 


 hν 
Creazione di Coppie elettroni-positroni
La creazione di coppie e+e- in seguito ad un fotone che interagisce con la materia avviene nel campo
del nucleo, immaginato circondato da una "nube" di elettroni e
epositroni "virtuali". D'altronde è evidente dai principi di
E1 p1
conservazione dell'energia e dell'impulso che non si tratta di
γ
creazione in quanto il processo non avviene nel vuoto. Infatti se
hν
così fosse avremo:
hν = E1 + E2
E2 p
hν ≤ c(p1+p2)
2
Il segno uguale vale solo nel caso in cui e+e- vanno nella stessa
direzione. Analizziamo questo caso. Quadrando le due si ha:
hν 2 = 2m 2 + 2 E1 E 2 + p12 + p 22
e+
hν 2 = p12 + p 22 + 2 p1 p 2
Se facciamo ora la differenza abbiamo: 0 = 2m2+2E1E2-2p1p2 ossia E1E2-p1p2 = -m2 che e' un
assurdo!!!
Infatti: E1 E 2 =
(m 2 + p12 )(m 2 + p22 ) =
(
che è sicuramente maggiore di p1p2 e quindi non può dare -m2.
7Heitler,
)
m 2 m 2 + p12 + p 22 + p12 p 22
Quantum Theory of Radiation, Oxford, 1954
129
Nel campo del nucleo, composto da coppie virtuali di e+e-, la "creazione" di coppie può essere
schematizzata come in figura
Il fotone diffonde le coppie virtuali che circondano il
nucleo. Dei due almeno uno si accoppia con la carica
elettrica del nucleo. Se si contraggono i vertici 1 e 2 si
ottiene un nuovo grafico che rappresenta la sezione
d'urto di Thomson.
Allora comprendiamo che la produzione di coppie è
anch'essa legata al processo Thomson con in più
l'accoppiamento 3 del fotone finale al nucleo di carica Z.
Quindi possiamo dire che la sezione d'urto per produzione
di coppie, σpair, sarà data da quella Thomson σ T
moltiplicata per un fattore che tiene conto del vertice 3.
Quest'ultimo sarà legato alla costante di struttura fine α o
meglio alla carica al quadrato (nel Thomson compare e4). Poiché la carica in gioco nel vertice 3 è Z
allora la sezione d'urto risulterà: σ pair = σ T Z 2α ≈ Z 2αr02 .
Quella esatta asintotica è:
 28 
−1  2 
σ pair = Z 2αr02  ln 183Z 3  − 
 27 
 9 


nel limite di energia del fotone Eγ molto maggiore dell'energia di soglia Et = 2me. Per energie
intermedie si ha:
 7  2 E  109 
σ pair = Z 2αr02  ln 
−

2
 9  mc  54 
Quella asintotica può essere messa in una forma estremamente semplice esprimendola in funzione di
Xo, definita come la lunghezza necessaria affinché un elettrone degradi la sua energia di un fattore
1/e di quella iniziale. Si ottiene:
σ pair ≈
[
]
7 1
in cui X 0 = gr cm 2
9 NX 0
N = numero di atomi per grammo
130
131
Bremsstrahlung
In questo paragrafo tratteremo la radiazione emessa da una particella carica quindi la sua locazione
sembrerebbe impropria però, dato il particolare tipo di trattazione unificata si vedrà che non è del
tutto inappropriato.
Energia critica
Gli elettroni che attraversano la materia perdono energia per ionizzazione e per bremsstrahlung. Le
due perdite sono profondamente diverse in energia. In genere, sopra una certa energia, detta critica,
predominano le perdite per bremsstrahlung, al di sotto, quelle per ionizzazione. Questa energia è
data in modo approssimato da:
(dE dx )irr.
(dE dx )ion.
≈
Z
Ec
800
[MeV ]
da cui l'energia critica Ec :
Ec ≈
[MeV]
800
Z
Alcuni valori tipici sono riportati nella seguente tabella.
Ec [MeV]
elemento
C
Al
Pb
103
47
6.9
Questi valori stanno a significare, approssimativamente, che un elettrone da 110, 50 e 7 MeV
rispettivamente in C, Al e Pb perde energia quasi esclusivamente per bremsstrahlung.
Irraggiamento degli elettroni
In seguito all'accelerazione che una particella carica subisce da parte del campo elettrico del nucleo
nell'attraversare la materia, la stessa emette energia e.m. secondo la formula di Larmor (già vista
nell'effetto Thomson). Poiché l'energia è proporzionale al quadrato dell'accelerazione, essa dipenderà
dall'inverso della massa al quadrato:
dW ∝ v& 2 ∝
1
m2
Perciò questo processo è prevalente nelle particelle leggere: me ∼ 0.5 MeV, µ ∼ 200 me, quindi un µ
perderà molto meno energia per irraggiamento [ (1/200)2] rispetto ad un elettrone. Il processo, che
non può avvenire nel vuoto come anche per la
γ
produzione di coppie in quanto è necessario un
campo che assorba l'impulso di rinculo del fotone
e
emesso, può essere schematizzato come segue:
L'elettrone emette un fotone e poi diffonde
scambiando un fotone col nucleo. I vertici 2 e 3
e
sono identici a quelli del processo di coppia. Il
vertice 1, se si considera che qui c'è un elettrone
e nella produzione di coppie c'è un positrone,
3
risulta praticamente simile.
Occorrerà però
Nucleo di carica Ze
pesare la σ con la probabilità di emettere un
fotone di una data energia , ossia, a parità di
132
energia totale irraggiata, saranno più numerosi quelli di bassa energia. Quindi, dato un elettrone di
energia E0, la probabilità, la σ, che sia un fotone di energia hν, nell'intervallo dν, sarà:
σ Br (ν )dν ≈ σ pair ⋅
dν
dν
≈ σ T Z 2α
ν
ν
La formula esatta per energie relativistiche [γ >> 1] è:
2


−1
2
dE ′  
E′ 
E ′    
 ⋅ ln 183Z 3
 − 1 −
1 + 1 −
σ (E 0 , E ′)dE ′ = 4 Z 2αr02
3  E 0   
E ′   E0 
  

dove

 1
 + 1 − E ′  
 9  E 0  


E 0 è l' energia iniziale dell' elettrone
E ′ è l' energia del quanto irradiato
Integrando, moltiplicando per il numero di atomi e per l'energia di ciascun fotone si ottiene l'energia
media persa per irraggiamento:
d E
−1
1

−
= 4αNZ 2 r02 ln183Z 3  +  ⋅ E 0
dx
 8
 
irr .
che può essere espressa più semplicemente tramite Xo. Si ottiene infatti:
−
d E
dx
≈
[
E0
con X 0 g cm 2
X0
]
irr .
dalla quale si deduce la definizione di X0 : per x = X0 → E(X0) = E0/e.
Con l'aumentare dell'energia la radiazione viene sempre emessa nella direzione di volo della
particella.
dσ
≈
dΩ
B
(m 2 c 4 + E 02θ 2 )2
e l'angolo medio di emissione risulta dell'ordine di: < θ >≈
mc 2
E0
Annichilazione Positroni Elettroni
Un positrone può annichilire incontrando un elettrone atomico e mettendo uno o più fotoni.
L'emissione di un solo fotone è cinematicamente possibile solo nel campo del nucleo, in quanto
quest'ultimo assorbe l'impulso di rinculo. Nel regime non relativistico il processo è simile al
Thomson con la variante che al diminuire della velocità del positrone il processo diventa più
probabile in quanto questa confrontabile con la velocità degli elettroni atomici. La sezione d'urto del
processo sarà allora:
σ
r2
c
σ + − ≈ T ≈ π 0 ≈ πro2
e e
v
β
β
in generale avremo:
1 − v2
σ + − = πr02
e e
4v
La distribuzione per E >>mc2 sarà:
(
)
 3 − v4 1 + v

ln
− 2 − v2 

1− v

 v
133
dσ
=
dΩ e+ e−
r02m 2

m 2 
2 E 2 θ 2 +

E 2 

Produzione di Sciami Elettromagnetici
Quando un elettrone o un γ attraversano la materia, in seguito al concatenamento di vari processi
(Compton, coppie, Br., annichilazione,...) si possono produrre degli sciami e.m.. La trattazione
analitica del processo è praticamente impossibile se si
vogliono ottenere risultati vicini alla realtà.
Vediamo come ha luogo il processo. Supponiamo che un
fotone incida su un nucleo; se l'energia è sufficiente si può
+ −
produrre una coppia e e ; ognuna di queste particelle
perderà energia per bremsstrahlung emettendo fotoni. I
fotoni emessi continueranno il percorso nel la materia
producendo altre coppie. Si ha così uno sciame di
particelle. Wilson [8] per primo trattò il problema con uno
studio di MonteCarlo ed ha ottenuto:
• Il range medio di un elettrone di energia iniziale Eo:
 E0

r = ln 2 ln 
+ 1
 Ec ln 2 
•
La distribuzione del range intorno a <r> è di tipo Gaussiano e la radice quadrata dello
Straggling quadratico medio è[9]:
 rE
S = r ln 2 1 − c
E0

•



Rozzamente si può prevedere il numero di particelle, nel punto di massimo sviluppo, cioè di
massima crescita:
E
E
n( x = xmax ) ≈ 0.15 0 ln 0
Ec Ec
con E0 = energia iniziale ed Ec = energia critica.
•
La penetrazione dello sciame al massimo dello sviluppo è: x(I max ) ≈ ln
•
1
E
2
2
≈ 0.8 s
L'allargamento (spread) laterale al massimo dello sviluppo è:  x 


Ec
8
9
vedi R. R. Wilson Phys. Rev. 84,100 (1951)
vedi B. Rossi-K. Greisen Revs. Mod. Phy. 13,240 (1941)
E0
in unità di X0.
Ec
134
•
L'allargamento angolare invece è : θ
2
1
2
E
≈ 0.75 s espresso in radianti e con Es ≈ 21
Ec
MeV
Quadro riassuntivo
Facciamo ora un quadro riassuntivo delle interazioni e.m. nella materia:
Processo
vs. Z (numero atomico) vs. Energia
Fotoelettrico
Z4- Z5
∼ E-3.5 - E-1
Compton
Coppie
Irraggiamento
vs. Massa
-
2
∼E-1 lnE
lnE
2
E
M-2
-
Z
Z
Z
Z
-
β-2
Qui di seguito è riportato un grafico in cui è possibile vedere i vari contributi portati alla sezione
d'urto dai processi sopra descritti.
Ionizzazione