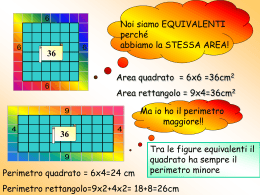
Da un problema assegnato
all’Esame di Stato 2006
Un filo metallico di lunghezza L viene
utilizzato per delimitare il perimetro di
un’aiuola rettangolare.
Qual è l’aiuola di area massima che è
possibile delimitare?
Reazioni nelle scuole
Commento di alcuni studenti:
“Non provo neanche a risolvere questo
problema: è proprio molto difficile!”
Commento di altri studenti:
Che fortuna! È facilissimo!
È il problema dello spago!
Perché il problema dello spago?
Ecco un esperimento per vedere il filo
metallico che può delimitare tante
aiuole rettangolari
Il problema dello spago
Si intuisce che si ha l’area massima nel
caso del quadrato.
Come si può dimostrare questa congettura?
Attività 1: problema dello spago
Dividetevi in gruppi di 2 – 4 persone.
Ad ogni gruppo viene data una scheda di
lavoro da completare.
Avete 40 minuti di tempo
Che cosa abbiamo trovato?
Due procedimenti per dimostrare la
congettura
1. Solo con prodotti notevoli
0 ≤ x ≤ 10
L’area S dei rettangoli è data da:
S = (10 + x)(10 – x) = 100 – x2
S è massima è 100, raggiunta solo se x = 0.
Così tolgo 0 a 100 e rimane il quadrato,
che ha area massima.
2. Con la geometria analitica
0 ≤ x ≤ 20
L’area S del rettangolo è data da:
S = xy
Con semiperimetro 20 e perciò
x + y = 20 da cui y = 20 − x
Esprimo l’area S in funzione della sola x
S = x(20 – x)
Il grafico
Eseguo la moltiplicazione indicata e scrivo
la funzione ‘area S variabile al variare di x’
S = – x2 + 20x con 0 ≤ x ≤ 20
Arco di parabola con vertice V(10, 100)
S massima è 100, raggiunta per x = 10, cioè
nel quadrato con i lati tutti lunghi 10.
Il perimetro deve essere 40 cm?
In tutti e due i procedimenti i rettangoli
avevano il perimetro lungo 40cm.
Se il perimetro è lungo 16 o 30 o 80cm , …
cambia la dimostrazione? NO!
Infatti, nel problema d’Esame trovo:
‘Un filo metallico di lunghezza L …’
Il perimetro è indicato con una lettera (L) per
ricordare che può essere scelto a piacere, senza però
cambiarlo mentre risolvo il problema.
In conclusione
I due procedimenti dimostrano che:
L’aiuola quadrata ha area massima fra
tutte le aiuole rettangolari delimitate con
un filo lungo L.
Esprimo la conclusione con il
linguaggio della geometria.
Il quadrato ha area massima fra tutti i
rettangoli che hanno un dato perimetro.