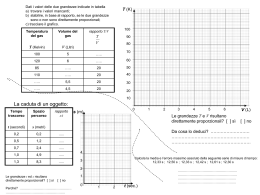
1 - GRANDEZZE E MISURE
INDICE
Grandezze fisiche e loro misure: 2
Notazione: 3
Prefissi: 4
Grandezze fondamentali e unità di misura: 5
Grandezze derivate: 9
Valori ed errori, incertezza di misura: 12
Come si risolve un esercizio di fisica: 14
2 - GRANDEZZE E MISURE
Una grandezza fisica si
misura
Quindi la misura di una
grandezza fisica non è,
in genere, un numero
puro.
Si deve sempre
precisare l'unità di
misura.
Il tavolo è lungo 2,2 m
Misurare significa
confrontare con un
campione
Il campione va definito
in modo operativo e se
ne utilizzano MULTIPLI
e SOTTOMULTIPLI
3 - NOTAZIONI
Il valore numerico di una
grandezza richiede
attenzione. Si può
scrivere:
1,2 m
1,2354 m
1 234 000 000 km
63 000 m
63 km
0,00012 cm
Conviene utilizzare la
notazione
ESPONENZIALE (o
scientifica):
1 234 000 000 km =
1,234 1012 m
0,00012 cm = 1,2 10-6
m
63 000 m e 63 km
sono espressioni
equivalenti;
1,2354 m non è
equivalente a 1,2
m;
1.2 in notazione
anglosassone
significa 1,2;
1 234 000 000 km
e 0,00012 cm
sono da evitare.
... oppure multipli e
sottomultipli
opportuni. Molti
sono noti:
km, m, dm, cm, mm,
ossia
kilo-, deci-, centi-,
milliMa ce ne sono
altri ...
4 -NOTAZIONE SCIENTIFICA
PREFISSI
Prefisso (si
legge)
valore
T (tera)
G (giga)
M (mega) h2
k (chilo)
1012
109
106
103
m (milli)
µ (micro)
n (nano)
p (pico)
f (femto)
10-3
10-6
10-9
10-12
10-15
Esempi:
2 µm = 2 10-6 m
1,25 ns = 1,25 10-9 s
103,3 MHz = 103,3 106 Hz = 1,033
108 cicli/s
...
4 -NOTAZIONE SCIENTIFICA
PREFISSI
Prefisso (si
legge)
valore
T (tera)
G (giga)
M (mega) h2
k (chilo)
1012
109
106
103
m (milli)
µ (micro)
n (nano)
p (pico)
f (femto)
10-3
10-6
10-9
10-12
10-15
5 - GRANDEZZE FISICHE FONDAMENTALI E DERIVATE
Ci sono alcune misure
fondamentali che siamo
in grado di compiere, ad
esempio quelle di
lunghezza
e comunque ci sono
grandezze derivate
Altre si riducono
operativamente a
misure di lunghezza
40,2 C equivale a 7,2
cm sulla scala
graduata
Altro esempio: la
misura della velocità
implica una misura di
distanza ed una di
tempo
nel senso che la loro
definizione si basa su
più misure
fondamentali:
Volume=axbxc=0.2 m3
v = L/T =10 m/s
6 - GRANDEZZE FISICHE FONDAMENTALI
Occorre quindi innanzitutto un sistema di campioni e di
strumenti di misura per le grandezze fondamentali
Sistema Internazionale ( S.I. )
http://physics.nist.gov/Units
Grandezza
Unità di misura
Lunghezza
Tempo
Massa
m (metro)
s (secondo)
kg (chilogrammo)
7 - GRANDEZZE FONDAMENTALI:
IL TEMPO
La definizione pratica di tempo è basata
sull'osservazione di fenomeni periodici.
Due fenomeni periodici consentono un confronto (una
verifica della loro periodicità).
Galileo utilizzò il battito del suo polso
per confermare l'isocronia del pendolo
Quindi il pendolo si può sfruttare per
costruire orologi.
Una misura accurata di sottomultipli piccoli del
secondo richiede pendoli con periodi sempre più brevi
(pendoli sempre più piccoli), ad es.:
le oscillazioni di un cristallo piezoelettrico (quarzo)
le oscillazioni della carica attorno ad un atomo di
Cesio
7 - GRANDEZZE FONDAMENTALI:
IL TEMPO:
Orologio al Cesio
Sfrutta l'oscillazione
tra due livelli
energetici
dell'atomo di Cesio.
9 192 631 770
periodi di tale
oscillazione
corrispondono ad
1s
7 - GRANDEZZE FONDAMENTALI:
LA LUNGHEZZA
La definizione pratica di lunghezza è basata sul
confronto con campioni.
Esempi storici sono:
il piede di Luigi XIV
il metro campione di Sevres.
Si deve poter replicare il campione per uso pratico.
Il campione attuale è il metro, definito come
lo spazio percorso dalla luce in 1/299 792 458 s
(quindi presuppone che la velocià della luce sia
costante,
c=299 792 458 m/s
e richiede che sia già stato definito il secondo)
8 - GRANDEZZE FONDAMENTALI:
LA MASSA
La massa misura la quantità di materia.
Si distingue la massa inerziale da quella gravitazionale
(la forza peso):
Le forze determinano i cambiamenti dello stato di
moto: F= m a
Anche la particolare forza peso: F peso= mg è
proporzionale alla massa.
In pratica la massa è misurata con bilance che saggiano
la forza peso:
confrontando con
campioni
oppure con altre forze note
(la forza elastica della
molla)
9 - GRANDEZZE DERIVATE:
LA DENSITÀ
Pesa di più un chilo di piombo o un chilo di piume?
Quel che distingue piume e
piombo è la DENSITÀ.
Principio di Archimede:
galleggiano in acqua gli oggetti
di densità media minore di
quella dell'acqua
La densità è definita come:
e nel Sistema Internazionale si misura in kg/m3
(l'acqua a 20 °C ha densità di 1000 kg/m3 = 1 g/cm3 = 1
kg/l)
10 - UN ESEMPIO DI CALCOLO:
Supponiamo di voler determinare la densità di un
materiale misurandone il volume e la massa.
Il nostro campione di questo materiale è un cubo di lato
l = 3.4 cm e ha massa M = 0,12 kg. Quanto vale la sua
densità?
Con la calcolatrice
M/l3 = 3.0531243639 103 kg/m3
In mancanza di una stima dell'incertezza si conservano
le cifre significative dei termini (0.12 e 3.4 ne hanno due
entrambi):
M/l3 = 3.1 103 kg/m3
11 - ANALISI DIMENSIONALE
Il fatto che le grandezze fisiche abbiano associata una
dimensione ha due importanti conseguenze pratiche
1.In ogni relazione tra diverse grandezze le dimensioni
delle due espressioni uguagliate devono essere le
stesse.
2.Se una legge è espressa da funzioni
trigonometriche, esponenziali, logaritmiche,
l'argomento di queste deve essere adimensionale
Ad esempio:
Nella legge di Ohm il prodotto
di Ampere per Ohm deve
V=IR
coincidere con l'unità di
misura Volt
La tensione di rete oscilla
sinusoidalmente nel tempo e
la sua pulsazione, , va
misurata in s-1, in modo che
sia adimensionale
14 - UN ESERCIZIO DI FISICA MOLTO SEMPLICE:
Si misura il diametro di una sfera con un calibro senza
nonio (precisione 1mm) e risulta D=4.0 cm; si pesa la
sfera e se ne determina la massa M=0.440(1) kg.
Calcolare la densità
del materiale.
15 - Altri esercizi
1.La distanza media Sole-Terra è 390 volte la distanza
Terra-Luna
N=dST/dTL=390
Durante l'eclissi totale di Sole la Luna si trova tra la
Terra ed il Sole ed oscura completamente l'immagine
di quest'ultimo in un punto della Terra. Calcolare:
il rapporto tra il raggio della Luna e quello del
Sole, RL/RS
il rapporto tra il volume della Luna e quello del
Sole, VL/VS
il raggio del Sole, RS, sapendo che la distanza
dTL=3,82 105 km e l'angolo sotto cui si vede la
Luna è di 0,52 gradi
2.Sapendo che in una unità di massa atomica vale
u=1,661 10-27 kg e che un atomo di idrogeno pesa
mH=1,00782504 u , quanti atomi ci sono in un kg di
idrogeno?