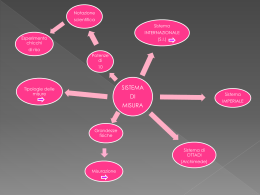
Prof. A. Di Muro
Grandezze fisiche
Una grandezza fisica è una caratteristica di un fenomeno che può essere misurata da uno strumento di
misura. L’intelligenza, la bontà, la bellezza ecc, non sono grandezze fisiche.
Grandezze fondamentali e derivate
Le grandezze fisiche si possono dividere in due grandi categorie:


Grandezze fondamentali. Sono quelle grandezze a partire dalle quali si possono costruire e
derivare tutte le altre. Le loro unità di misura possono essere scelte tutte in maniera indipendente
l'una dall'altra.
Grandezze derivate. Sono quelle grandezze che si possono derivare, tramite opportune formule
matematiche, dalle grandezze fisiche fondamentali.
La scelta di quali siano le grandezze fondamentali e quali siano le grandezze derivate è convenzionale.
Nel 1960 con la Conferenza Generale dei Pesi e delle Misure che introdusse il Sistema Internazionale.
In tale occasione si scelsero le sette grandezze fisiche fondamentali e le sette relative unità di misura:
Il Sistema Internazionale (SI) delle unità di misura
Grandezza fondamentale Unità di misura Simbolo della unità di misura
Simbolo dimensionale
lunghezza
metro
m
L
massa
kilogrammo
kg
M
tempo
secondo
s
T
intensità di corrente
ampere
A
i, A
temperatura
kelvin
K
K
intensità luminosa
candela
cd
l, cd
quantità di sostanza
mole
mol
m, mol
Analisi dimensionale
Per ogni grandezza fondamentale si introduce il simbolo dimensionale o dimensione, che deve essere
racchiuso fra parentesi quadre.
Se due grandezze fisiche hanno le stesse dimensioni si dicono omogenee.
Le dimensioni di una grandezza derivata si ricavano dalla relazione che lega questa alle grandezze
fondamentali.
Per esempio, la velocità è una grandezza derivata perché si costruisce a partire dalle grandezze lunghezza
e tempo, analogamente l’accelerazione:
v
 L
x
con equazione dimensionale  v  
t
T 
Le grandezze fisiche adimensionali sono prive di dimensioni e definite come rapporto fra due grandezze
omogenee, esempio gli angoli.
Prof. A. Di Muro
Le equazioni dimensionali sono utili per determinare se una formula fisica è sbagliata o per
determinare la dimensione di una grandezza fisica.
esempio:
mx
dove F è una forza, m la massa, x una lunghezza e v la velocità, si ha
v
 L  M  L
 L
 M  2  L da cui si capisce che è sbagliata  M  2   M T 
 
T 
T 
T 
mm
Oppure dalla formula F  G 1 2 2 dove F è una forza, m la massa, d una lunghezza, determinare la
d
dimensione di G
data la formula F 
 L
M 
 M  2  G  2
T 
 L
 L 
si ricava G  
2
 M T 
2
3
Multipli e sottomultipli nel Sistema Internazionale
fattore di
moltiplicazione
prefisso
simbolo
10 24
yotta
Y
10
21
zetta
Z
10
18
exa
E
10
15
peta
P
10
12
tera
T
10
9
giga
G
10
6
mega
M
10
3
chilo
k
10
2
etto
h
10
1
deca
da
10
-1
deci
d
10
-2
centi
c
10
-3
milli
m
10
-6
micro
µ
10
-9
nano
n
10
-12
pico
p
10
-15
femto
f
10
-18
atto
a
10
-21
zepto
z
10
-24
yocto
y
Prof. A. Di Muro
È utile saper convertire le unità di misura tra grandezze omogenee.
Esempi:
convertire 2.8 m in km:
2.8 m  2.8 106 m  2.8 106 100 m  2.8 106 103 103 m  2.8 106 103 km  2.8 109 km
convertire 2.8 mm2 in hm2:
2.8 mm2  2.8 ( 103 m )2  2.8 ( 103 100 m )2  2.8 ( 103 102102 m )2  2.8 ( 103 102 hm )2  2.8 1010 hm2
convertire 2.8 pm3 in cm3:
2.8 pm3  2.8 ( 1012 m )3  2.8 ( 1012 100 m )3  2.8 ( 1012 102102 m )3  2.8 (1012 102 cm )3  2.8 10 30 cm3
convertire 1
1
mm
km
in
:
h
ns
mm 103 m 103100 m 103103103 m 103103 3.6 103 km
km
 9 


 3.6106
9
ns 10 s 109 3600 s 109 h
10 h
h
3600
3.6 103
Cifre significative ( C.S.)
Dal punto di vista matematico i numeri 3.58 e 3.580 rappresentano lo stesso numero, in fisica
rappresentano due numeri diversi e la diversità sta nel grado di precisione che questi due numeri
esprimono. Il primo indica un numero tra 3.57 e 3.59, invece il secondo indica un numero compreso tra
3.579 e 3.581. Diciamo che il secondo numero ha più cifre significative del primo.
Cifra più significativa
Cifra meno significativa
0.0258



La cifra più significativa è sempre la prima da sinistra che sia diversa da zero;
La cifra meno significativa
o in un valore intero, è la prima da destra che sia diversa da zero,
o in un valore con una parte frazionaria, è l'ultima cifra a destra, anche se si tratta di uno
zero;
Le cifre significative sono tutte quelle comprese tra la più significativa e la meno significativa,
queste incluse.
p.es. 0.0810 ha tre C.S.
Prof. A. Di Muro
Regole di calcolo:
Somme e sottrazioni
Nel risultato compaiono solo le cifre nelle posizioni decimali dell’operando con meno cifre; ad esempio:
2.3  3.24  5.5 ,
6.25  2.471  3.78 ,
4 102  3  4 102 ,
4.00 102  3  3.97 102
Prodotti e divisioni
Un criterio utile, ma approssimato, è quello che il risultato deve avere lo stesso numero di cifre
significative dell’operando che ne ha di meno
2.587  4.6 = 12 ,
42.36 : 28.3 = 1.50
Notazione scientifica
Per scrivere un numero nella notazione scientifica occorre trasformare il numero in un prodotto di due
fattori, un coefficiente compreso tra 1 e 10 ed una potenza in base 10.
p. es. 152.8 = 1.528 10 2.
Ordine di grandezza
Quando si scrive un numero nella notazione scientifica, la potenza in base 10 fornisce l’ordine di
grandezza del numero.
Occorre fare attenzione perché l'ordine di grandezza di 6.1 10 6 è 10 7 e non 10 6, perché 6.1 è più vicino a
10 che a 1.
L'uso dell'ordine di grandezza è indispensabile in fisica, per esempio le lunghezze variano da un
10 – 15 m per le dimensioni nucleari fino a 10 28 m per le galassie più lontane.
Approssimazione
I numeri vanno approssimati alla cifra meno significativa, a tal fine occorre osservare la prima cifra non
significativa, se questa è minore di cinque l’approssimazione è per difetto, se è maggiore o uguale a
cinque l’approssimazione è per eccesso.
Esempio:
approssimare 2.5608 alla terza C.S. 2.56
approssimare 0.4859 alla seconda C.S. 0.49