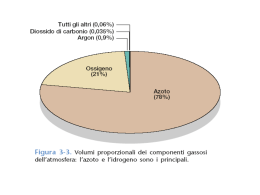
Lo Stato Gassoso: Alcune Caratteristiche
Sebbene possano avere proprietà chimiche distinte, le sostanze in fase gas
hanno caratteristiche fisiche molto simili, in quanto le particelle (atomi o
molecole) sono molto distanti le une dalle altre:
ELEVATA COMPRIMIBILITÀ:
Al contrario di solidi e liquidi, se sottoposti a pressione i gas si comprimono in
modo significativo.
ASSENZA DI VOLUME PROPRIO:
All’elevata comprimibilità corrisponde una elevata capacità di espansione. Un
gas si espande spontaneamente ad occupare tutto il volume a disposizione. Il
volume di un gas coincide con quello del suo contenitore.
ASSENZA DI FORMA CARATTERISTICA:
Un gas assume non solo il volume, ma anche la forma del suo contenitore.
FORMAZIONE DI MISCELE OMOGENEE:
Nonostante abbiano proprietà chimiche diverse, i gas formano sempre miscele
omogenee, in qualunque proporzione vengano mescolati. Ne è un esempio
l’atmosfera.
Ripassiamo: il Concetto di Pressione e la Pressione Atmosferica
Si definisce PRESSIONE P la forza F esercitata su una data superficie di area A:
P = F/A = (m a)/A
L’unità della pressione nel Sistema Internazionale è il Pascal (Pa)
1 Pa = 1 N/m2 = (kg m/s2)/m2
Gli atomi e le molecole che compongono i gas dell’atmosfera sono soggetti ad
attrazione gravitazionale. L’energia cinetica delle particelle di gas contrasta solo
in parte la forza gravitazionale e i gas atmosferici esercitano sulla superficie
terrestre
una
pressione,
detta
PRESSIONE
ATMOSFERICA.
Si consideri una colonna di aria base 1 m2 e di
massa 104 kg. La pressione esercitata da tale
colonna sulla superficie terrestre è pari a
P = F/A = (104 kg)(9,8 m s2)/1 m2 = 1,01325×105 Pa
Evangelista Torricelli (1608-1647), studente di Galileo, inventò il barometro per
dimostrare che l’atmosfera avesse peso.
Un tubo in vetro, chiuso a un’estremità, lungo più di 760
mm e riempito completamente di mercurio è inserito,
capovolto, in un contenitore in cui è presente mercurio.
Dopo il capovolgimento, non tutto il mercurio presente
nel tubo fuoriesce, a evidenza del fatto che il mercurio del
contenitore trasmette a quello nel tubo la pressione
esercitata sulla sua superficie dall’atmosfera. L’altezza del tubo è una misura di
tale pressione e cambia in funzione di quest’ultima.
La PRESSIONE ATMOSFERICA STANDARD è la pressione adeguata a sostenere
una colonna di mercurio alta 760 mm. Tale pressione è pari a 1,01325×105 Pa.
Oltre al Pascal esistono altre unità di misura, piuttosto comuni anche se non
adottate del Sistema Internazionale:
1 atm = 760 mm Hg = 760 torr = 1,01325×105 Pa = 1,01325 bar
Lo Stato Gassoso e la Tavola Periodica
11 elementi (O), a temperatura e pressione ambiente, si trovano in fase gas:
H, N, O, F, Cl, He, Ne, Ar, Kr, Xe, Rn
(H, N, O, F, Cl come molecole biatomiche X2)
Rapporto tra Volume e Pressione: la Legge di Boyle
È esperienza comune che, prendendo quota allontanandosi
dalla superficie terrestre, i palloni atmosferici si espandano.
Ovvero, il volume di un gas aumenta al diminuire della
pressione esercitata su di esso.
Il chimico inglese Robert Boyle (1627-1691) fu il primo a
studiare il rapporto tra pressione e volume di un gas,
mediante l’apparato di cui sotto.
A una data temperatura, una quantità
nota di gas è bloccata in un tubo “a J” da
una colonna di mercurio. Aumentando la
quantità di mercurio, i.e. aumentando la
pressione a cui il gas è sottoposto, questo
si contrae e occupa un volume minore.
Boyle razionalizzò le sue osservazioni mediante una relazione empirica nota
come LEGGE DI BOYLE:
P × V = costante (a temperatura T e numero di moli n costante)
V = costante/P
(a temperatura T e numero di moli n costante)
Il volume di una data quantità di gas mantenuto a temperatura costante è
inversamente proporzionale alla pressione. Graficamente:
La respirazione è un esempio di applicazione della
legge di Boyle. Durante l’inspirazione il torace si
dilata, i polmoni aumentano il proprio volume, il
gas contenuto diminuisce la propria pressione e
consente
l’ingresso
l’espirazione,
il
all’aria
torace
si
esterna.
contrae,
Durante
i
polmoni
diminuiscono il proprio volume, il gas contenuto
aumenta la propria pressione e riesce a fuoriuscire.
Rapporto tra Volume e Temperatura: la Legge di Charles
Si può facilmente verificare che, a pressione costante,
il volume di una data quantità di gas aumenta
all’aumentare
della
temperatura,
diminuisce
al
diminuire della temperatura.
Fu lo scienziato francese Jacques Charles (1746-1823) a evidenziare il rapporto
tra temperatura e volume di un gas, con osservazioni come quella del grafico:
Nel
1848,
William
Thompson
(1824-1907), più noto come Lord
Kelvin, introdusse una scala di
temperatura assoluta, la SCALA
KELVIN (0 K = -273,15 °C).
Charles razionalizzò le sue osservazioni mediante una relazione empirica nota
come LEGGE DI CHARLES:
V/T = costante
(a pressione P e numero di moli n costante)
V = costante × T (a pressione P e numero di moli n costante)
Il volume di una data quantità di gas mantenuto a pressione costante è
direttamente proporzionale alla temperatura assoluta.
Rapporto tra Volume e Moli: L’Ipotesi di Avogadro
Nel 1808, sulla base delle sue osservazioni, Joseph Louis Gay-Lussac (17781823) enunciò la LEGGE DELLA COMBINAZIONE DEI VOLUMI: a pressione e
temperatura date, i rapporti dei volumi di gas che reagiscono tra loro sono
numeri piccoli interi (e.g. 2 volumi di idrogeno molecolare reagiscono con un
volume di ossigeno molecolare a dare due volumi di vapore acqueo).
Nel 1811 Amedeo Avogadro (1776-1856) interpretò le osservazioni di Gay-Lussac
con l’IPOTESI DI AVOGADRO: volumi uguali di gas diversi alle stesse T e P
contengono lo stesso numero di ‘enti’ (i.e.. atomi o molecole):
In particolare, a T = 273,15 K e 1 atm, 22,4 L di
gas contengono 1 mole di particelle.
Dalla sua ipotesi Avogadro derivò quella che
prese il nome di LEGGE DI AVOGADRO:
V = costante × n
(a temperatura T e pressione P costanti)
La legge di Boyle può essere utilizzata per valutare come varia il volume di un
gas al variare della pressione (o viceversa) quando temperatura e numero di moli
sono costanti.
Stato iniziale:
PiVi = costante
Stato finale:
PfVf = costante
Ovvero:
PfVf = PiVi
Da cui
Vf = PiVi/Pf
oppure
Pf = PiVi/Vf
La legge di Charles può essere utilizzata per valutare come varia il volume di un
gas al variare della temperatura (o viceversa) quando pressione e numero di moli
sono costanti.
Stato iniziale:
Vi/Ti = costante
Stato finale:
Vf/Tf = costante
Ovvero:
Vf/Tf = Vi/Ti
Da cui
Vf = TfVi/Ti
oppure
Tf = VfTi/Vi
Analogamente per la legge di Avogadro. Verificarlo in autonomia…
L’Equazione di Stato dei Gas Ideali
Le leggi di Boyle, Charles e Avogadro esprimono relazioni di proporzionalità tra
due delle quattro grandezze T, P, V, n, qualora le altre due siano costanti:
Legge di Boyle
V ∝ 1/P
(n, T costanti)
Legge di Charles V ∝ T
(n, P costanti)
Legge di Avogadro V ∝ n
(P, T costanti)
Combinando le quattro relazioni si ottiene la relazione più generale V ∝ nT/P.
Identificata con R (COSTANTE DEI GAS) la costante di proporzionalità, si ha
l’EQUAZIONE DI STATO DEI GAS IDEALI:
V = nRT/P
L’equazione è valida per i GAS IDEALI, ovvero per gas tali che
le particelle (atomi o molecole) non interagiscono tra loro;
la somma dei volumi delle singole particelle è molto inferiore al volume
occupato dal gas.
R, COSTANTE DEI GAS, assume valori dipendenti dalle unità di misura con cui
si esprimono pressione e volume, fatto salvo che temperatura e quantità di
materia si esprimono in Kelvin e moli, rispettivamente:
Unità di Misura
Valore
(L atm)/(mol K)
0,08206
J/(mol K)
8,314
cal/(mol K)
1,987
(m3 Pa)/(mol K)
8,314
(L torr)/(mol K)
62,36
Si supponga di avere 1 mole di gas ideale a 1 atm e 273,15 K. Il volume
occupato dal gas, secondo l’equazione di stato dei gas ideali è pari a
V = nRT/P = [(1 mol) (0,08206 L atm/K mol) (273,15 K)] / 1 atm = 22,41 L
Le condizioni 0 °C e 1 atm vengono definite CONDIZIONI NORMALI DI
TEMPERATURA E PRESSIONE (NTP). La proprietà dei gas sono tipicamente
tabulate in condizioni NTP. 22,41 L è il VOLUME MOLARE di un gas a NTP.
Relazione tra Equazione di Stato dei Gas Ideali e Leggi dei Gas
Le leggi dei gas (Boyle, Charles, Avogadro) sono casi speciali dell’equazione di
stato dei gas ideali. A temperatura e numero di moli constanti, e.g., si ha
P V = nRT = costante
che è la legge di Boyle.
A pressione e numero di moli costanti si ha
V/T = nR/P = costante
che è la legge di Charles.
A pressione e temperatura costanti si ha
V/n = RT/P = costante
che è la legge di Avogadro.
Equazione di Stato, Massa Molare e Densità dei Gas Ideali
Dall’equazione di stato dei gas ideali è possibile ricavare informazioni sulla
densità (ρ) di un gas, nota la sua massa molare (PM):
n/V = P/RT
(n/V) × PM = (P/RT) × PM
ovvero
m/V = (P/RT) × PM
ρ = (P/RT) PM
Ovvero la densità di un gas dipende dalle sue pressione e temperatura.
Naturalmente, nota la densità del gas, è possibile calcolarne la massa molare.
In presenza di una miscela equimolare di gas a una data pressione, sebbene la
miscela sia omogenea, i gas si stratificano in ragione della loro temperatura
(ovvero in ragione della loro densità): i gas più caldi, i.e. meno densi, si trovano
più in alto di quelli più freddi. Per esempio:
La CO2 emessa da un estintore, più densa di N2 e O2, si stratifica in basso
impedendo all’O2 di raggiungere il materiale combustibile.
La differenza di densità tra aria calda e fredda è responsabile dell’ascensione
dei palloni aerostatici, nonché di molti fenomeni atmosferici.
Es.
Es. 1: Una bombola di 37,0 L contiene ossigeno (O2) alla pressione di 6,0 atm e
alla temperatura di 25 °C. Calcolare la massa di gas contenuta nella bombola.
m(O2) = n(O2)×PM(O2)
Ricordando PV = nRT si ha n = PV/RT
n(O2) = PV/RT
T = 25 + 273,15 = 298,15 K
R = 0,082 (L atm)/(mol K)
n(O2) = (6,0×37,0)/(0,082×298,15) = 8,4 mol
m(O2) = 8,4×32 = 269 g
Es.
Es. 2: 3,60 g di una sostanza gassosa occupano un volume di 1,98 L a 25 °C e
765 torr. Calcolare la massa molare del gas.
PM = m/n
Ricordando PV = nRT sia ha n = PV/RT
PM = m×RT/PV = (3,60×0,082×298,15)/(765/760×1,98) = 44,1 g/mol
Es.
Es. 3: Calcolare la densità del cloro (Cl2) a 56 °C e 730 torr.
d(Cl2) = m(Cl2)/V(Cl2)
m(Cl2) = n(Cl2)/(PM(Cl2)
n(Cl2) = PV(Cl2)/RT
d(Cl2) = PV(Cl2)/(RT/(PM(Cl2)/ V(Cl2) = P×PM(Cl2)/RT
d(Cl2) = (730/760×70,90)/(0,082×(56+273,15)) = 2,53 g/L
Es.
Es. 4: 500 mL di ossigeno (O2) a -70 °C e 730 torr vengono portati in condizioni
normali. Calcolare il volume finale e la massa del gas.
Vf = nfRTf/Pf oppure Vf = nf × 22,414
nf = ni = PiVi/RTi
Vf = PiVi/RTi × 22,414 = (730/760×0,500)/(0,082×(-70+273,15)) × 22,414 = 0,65 L
m = n×PM
m = PiVi × PM/RTi = (730/760×0,500×32,00)/(0,082×270,15) = 0,92 g
Es.
Es. 5: 5,6 L di un gas vengono compressi da 762 torr a 2,3 atm. Calcolare il volume del
gas dopo la compressione, avvenuta a temperatura costante.
Legge di Boyle: PV = costante
P iV i = P f V f
Vf = PiVi/Pf = (762/760×5,6)/2,3 = 2,3 L
Es.
Es. 6: Un tubo chiuso contenente aria alla pressione di 1 atm viene riscaldato da 10 °C
a 400 °C. Calcolare la pressione finale del gas.
P/T = costante
Pi/Ti = Pf/Tf
Pf = PiTf/Ti = [1×(400 + 273,15)]/(10 + 273,15) = 2,38 atm
Es.
Es. 7: Una bombola viene riempita con gas alla pressione di 20 atm e alla temperatura
di 25 °C. La bombola sopporta al massimo 35 atm. Fino a quale temperatura regge?
P/T = costante
Pi/Ti = Pf/Tf
Tf = TiPf/Pi = [(25 + 273,15) × 35]/20 = 521 K = 248 °C
Es.
Es. 8: Quanti litri di diossido di carbonio (CO2) si formano in condizioni normali per
combustione di 500 g di acido benzoico (C7H6O2)?
C7H6O2 + O2 → CO2 + H2O
C7H6O2 + n O2 → 7 CO2 + n’ H2O
Ricordando PV = nRT si ha V(CO2) = n(CO2)RT/P
n(CO2)?
Per ogni mole di acido benzoico consumata, si formano 7 moli di CO2.
n(CO2) = 7 × n(C7H6O2)
n(C7H6O2) = m(C7H6O2)/PM(C7H6O2)
V(CO2) = 7 × m(C7H6O2)/PM(C7H6O2) × RT/P
V(CO2) = (7 × 500 × 0,082 × 273,15)/(122 × 1) = 642,6 L
Es.
Es. 9: Un’autovettura consuma circa 8 L di ottano (C8H18) ogni 100 km. Quanti litri di
diossido di carbonio (CO2) si formano in condizioni normali per un percorso di 100 km
sapendo che d(C8H18) = 0,82 g/cm3?
C8H18 + O2 → CO2 + H2O
C8H18 + n O2 → 8 CO2 + n’ H2O
Ricordando PV = nRT si ha V(CO2) = n(CO2)RT/P
n(CO2)?
Per ogni mole di ottano consumata si formano 8 moli di CO2.
n(CO2) = 8 × n(C8H18)
n(C8H18) = m(C8H18) / PM(C8H18) = d(C8H18) × V(C8H18) / PM(C8H18)
V(CO2) = 8 × d(C8H18) × V(C8H18) / PM(C8H18) × RT/P
V(CO2) = 8 × 0,82×103 × 8 × 0,082 × 273,15/(114,26 × 1) = 10303 L
Es.
Es. 10:
10 Per combustione di 1,64 g di una miscela contenete zolfo e un materiale inerte,
si formano 952 mL di diossido di zolfo (SO2) a 25 °C e 0,850 atm. Determinare la
percentuale di zolfo nella miscela.
S + O2 → SO2
%(S) = m(S)/m(miscela) × 100
m(S)?
m(S) = n(S)/PM(S)
Per ogni mole di SO2 formatasi, si consuma una mole di zolfo.
n(S) = n(SO2)
n(SO2) = PV(SO2)/RT
m(S) = (PV(SO2)/RT)/PM(S) = PV(SO2) × PM(S)/RT
m(S) = 0,850 × 0,952 × 32,06 /(0,082 × 298,15) = 1,06 g
%(S) = 1,06/1,64 × 100 = 64,6%
Es.
Es. 11:
11 1,32 g di un idrocarburo gassoso alla pressione di 1 atm e alla temperatura di
25 °C occupano un volume di 1,15 L. Determinare la formula minima, la massa molare
e la formula molecolare dell’idrocarburo sapendo che C = 85,63% e H = 14,37%.
Elemento
%
PA, g/mol
Moli
Moli Normalizzate
NIntero
C
85,63
12,01
7,13
1
1
H
14,37
1,01
14,23
1,9958
2
Formula minima: CH2
PM(CH2) = 14,03 g/mol
PM(idrocarburo/PM(CH2) = 28,1/14,03 = 1,97 ≈ 2
Formula molecolare C2H4, etilene
1. PM = m/n
2. PV = nRT
PM = m/(PV/RT) = mRT/PV = (1,32 × 0,082 × 298,15)/(1 × 1,15) = 28,1 g/mol
Es.
Es. 12:
12 L’ossidazione metabolica del glucosio (C6H12O6) produce nel nostro corpo CO2:
C6H12O6(aq) + 6 O2(g) → 6 CO2(g) + 6 H2O(l)
La CO2 prodotta viene espulsa dai polmoni sotto forma di gas. Calcolare a) il volume di
CO2 secca prodotta alla temperatura corporea (37 °C) e a 0,970 atm quando si
consumano 24,5 g di glucosio; b) il volume di ossigeno necessario, a 1,00 atm e 298 K,
per ossidare completamente 50,0 g di glucosio.
a)
V(CO2) = n(CO2)RT/P
n(CO2) = 6 × n(C6H12O6) = 6 × m(C6H12O6)/PM(C6H12O6)
V(CO2) = [6×m(C6H12O6)/PM(C6H12O6)]×RT/P = [6×m(C6H12O6)×RT]/[PM(C6H12O6)×P]
V(O2) = (6 × 24,5 × 0,082 × 310,15)/(180,12 × 0,970) = 21,4 L
b)
V(O2) = n(O2)RT/P
n(O2) = 6 × n(C6H12O6) = 6 × m(C6H12O6)/PM(C6H12O6)
V(O2) = [6×m(C6H12O6)/PM(C6H12O6)] × RT/P = [6 × m(C6H12O6) × RT]/[PM(C6H12O6)× P]
V(O2) = (6 × 50,0 × 0,082 × 298)/(180,12 × 1) = 47,5 L
Es.
Es. 13:
13 4,15 g di carbonato di sodio (Na2CO3) vengono fatti reagire con acido solforico
(H2SO4) secondo la reazione
Na2CO3(aq) + H2SO4(aq) → Na2SO4(aq) + CO2(g) + H2O(l)
Il diossido di carbonio che si libera viene raccolto, dopo essicazione, in un recipiente di
5 L a 25 °C. Trovare a) la pressione del gas nel recipiente; b) quanto Na2CO3 si deve far
reagire per ottenere una pressione di CO2 di 1,40 atm alla stessa temperatura e nello
stesso contenitore.
a)
PV = n(CO2)RT ovvero P = n(CO2)RT/V
Per ogni mole di Na2CO3 consumata, si forma una mole di CO2.
n(CO2) = n(Na2CO3) = m(Na2CO3)/PM(Na2CO3)
P = m(Na2CO3)/PM(Na2CO3) × RT/V = [m(Na2CO3) × RT]/[PM(Na2CO3) × V]
P = (4,15 × 0,082 × 298,15)/(106,0 × 5) = 0,19 atm
b)
m(Na2CO3) = n(Na2CO3) × PM(Na2CO3)
n(Na2CO3) = n(CO2)
n(CO2) = PV/RT
m(Na2CO3) = (PV/RT) × PM(Na2CO3) = [PV × PM(Na2CO3)]/RT
m(Na2CO3) = (1,40 × 5 × 106,0)/(0,082 × 298,5) = 30,3 g
Miscele Di Gas e Pressioni Parziali: La Legge di Dalton
John Dalton (1766-1844) osservò che la pressione totale di una miscela di gas
(PTOT) eguaglia la somma delle pressioni (Pi, PRESSIONE PARZIALE DEL GAS i)
che ogni gas i eserciterebbe se fosse da solo nelle stesse condizioni di V e T:
PTOT =
Σi Pi = Σi ni (RT/V) = nTOT (RT/V)
Ovvero:
Ogni gas della miscela è indipendente dagli altri, obbedisce all’equazione di
stato dei gas ideali e vi posso associare la pressione parziale:
Pi = ni (RT/V)
A temperatura e volume costanti, la pressione totale è direttamente
proporzionale al numero di moli totali di gas presente, indipendentemente dalla
natura del gas e dal fatto che si tratti di un solo gas o di una miscela:
PTOT = nTOT (RT/V)
Poiché ogni gas si comporta in modo indipendente, posso correlare la sua
pressione parziale con la sua frazione molare χi in una data miscela:
χi = ni/nTOT = Pi (RT/V)/PTOT (RT/V) = Pi/PTOT
Miscele di Gas e Pressioni Volumi: la Legge di Amagat
Émile-Hilaire Amagat (1841-1915) osservò che il volume totale di una miscela di
gas (VTOT) eguaglia la somma dei volumi parziali (Vi) che ogni gas i possiederebbe
se fosse da solo nelle stesse condizioni di T e P:
VTOT =
Σi Vi = Σi ni (RT/P) = nTOT (RT/P)
Ovvero:
Ogni gas della miscela è indipendente dagli altri, obbedisce all’equazione di
stato dei gas ideali e vi posso associare il volume parziale:
Vi = ni (RT/P)
A temperatura e pressione costanti, il volume totale è direttamente
proporzionale al numero di moli totali di gas presente, indipendentemente dalla
natura del gas e dal fatto che si tratti di un solo gas o di una miscela:
VTOT = nTOT (RT/P)
Poiché ogni gas si comporta in modo indipendente, posso correlare il suo
volume parziale con la sua frazione molare χi in una data miscela:
χi = ni/nTOT = Vi (RT/P)/VTOT (RT/P) = Vi/VTOT
Es.
Es. 1: La concentrazione del diossido di carbonio (CO2) nell’atmosfera è di 390 L ogni
106 L di aria. Qual è la frazione molare del diossido di carbonio nell’atmosfera?
χi = Vi/VTOT
χ(CO2) = V(CO2)/VTOT = 390/ 106 = 39/ 105 = 39 × 10-5
Es.
Es. 2: Una miscela gassosa contenente 0,765 moli di He, 0,330 moli di Ne e 0,110 moli
di Ar è chiusa in un recipiente di 10,00 L a 25 °C. Calcolare a) la pressione parziale di
ogni gas e b) la pressione totale della miscela.
a)
Pi = niRT/V
P(He) = n(He) × RT/V = (0,765 × 0,082 × 298,15)/10,00 = 1,87 atm
P(Ne) = n(Ne) × RT/V = (0,330 × 0,082 × 298,15)/10,00 = 0,81 atm
P(Ar) = n(Ar) × RT/V = (0,110 × 0,082 × 298,15)/10,00 = 0,27 atm
b)
PTOT = Σi Pi
PTOT = + P(He) + P(Ne) + P(Ar) = 1,87 + 0,81 + 0,27 = 2,95 atm
Es.
Es. 3: Un palombaro utilizza bombola di 10,0 L di volume contenente 51,2 g di O2 e
32,6 g di He. Calcolare a) la pressione parziale di ogni gas e b) la pressione totale della
miscela se la temperatura è 19 °C.
a)
Pi = niRT/V
P(O2) = n(O2) × RT/V = [m(O2)/PM(O2)] × RT/V = [m(O2) × RT] / [PM(O2) × V]
P(O2) = (51,2 × 0,082 × 292,15)/(32,00 × 10,00) = 3,8 atm
P(He) = n(He) × RT/V = [m(He)/PA(He)] × RT/V = [m(He) × RT] / [PA(He) × V]
P(He) = (32,6 × 0,082 × 292,15)/(4,00 × 10,00) = 19,5 atm
b)
PTOT = Σi Pi
PTOT = P(O2) + P(He) = 3,8 + 19,5 = 23,3 atm
Es.
Es. 4: Un pezzo di CO2 solida di massa 5,50 g viene introdotto in un recipiente di 10,0
L che contiene aria a 705 torr e 24 °C. In queste condizioni il diossido di carbonio
sublima, ovvero passa dallo stato solido a quello gassoso. Qual è a) la pressione
parziale del diossido di carbonio e b) la pressione totale all’interno del contenitore nelle
condizioni di temperatura menzionate.
a)
Pi = niRT/V
P(CO2) = n(CO2) × RT/V = [m(CO2)/PM(CO2)] × RT/V = [m(CO2) × RT] / [PM(CO2) × V]
P(CO2) = (5,50 × 0,082 × 297,15)/(44,01 × 10,0) = 3,3 atm
b)
PTOT = Σi Pi
PTOT = P(CO2) + P(aria) = 3,3 + 705/760 = 4,2 atm
Es.
Es. 5: 5,00 mL di etere dietilico (C4H10O, densità 0,7134 g/mL) vengono introdotti in un
recipiente di 6,00 L che contiene già una miscela di ossigeno (O2) e azoto (N2) alle
rispettive pressioni parziali 0,208 atm e 0,751 atm. La temperatura è pari a 35 °C e
l’etere dietilico evapora totalmente. Calcolare a) la pressione parziale dell’etere dietilico
e b) la pressione totale nel contenitore.
a)
Pi = niRT/V
P(etere) = n(etere)×RT/V = [m(etere)/PM(etere)]×RT/V = [m(etere)×RT] / [PM(etere)×V]
m(etere) = d(etere) × V(etere)
P(etere) = [d(etere)×V(etere)×RT] / [PM(etere)×V]
P(etere) = (0,7134×103 × 5 ×10-3 × 0,082 × 308,15)/(74,50 × 6,00) = 0,20 atm
b)
PTOT = Σi Pi
PTOT = P(etere) + P(O2) + P(N2) = 0,20 + 0,208 + 0,751 = 1,16 atm
Es.
Es. 6: La pressione di una miscela contenente i gas CO2, C2H6, C2H4 è di 1,27 atm.
Dopo eliminazione di CO2 per reazione con Ba(OH)2, si sono ottenuti 1,46 g di BaCO3.
La pressione, misurata nelle stesse condizioni di volume e temperatura, è ridotta a 0,88
atm. Trovare a) la frazione molare di CO2 nella miscela iniziale di gas e b) il numero
totale di moli presenti nella miscela gassosa iniziale.
CO2(g) + Ba(OH)2(aq) → Ba(CO)3(s) + H2O(l)
a)
χ(CO2) = P(CO2)/PTOT(inizio)
P(CO2) = PTOT(inizio) – PTOT(fine) = 1,27 – 0,88 = 0,39 atm
χ(CO2) = 0,39/1,27 = 0,31
b)
χ(CO2) = n(CO2)/nTOT(inizio)
nTOT(inizio) = n(CO2) / χ(CO2)
n(CO2) = n(BaCO3) = m(BaCO3) / PM(BaCO3)
nTOT(inizio) = m(BaCO3) / [PM(BaCO3) × χ(CO2)] = 1,46 / (197,34 × 0,31) = 0,024 mol
Es.
Es. 7: Il pentafluoruro di iodio (IF5) gassoso può essere preparato secondo la reazione
I2(s) + 5 F2(g) → 2 IF5(g)
Un pallone da 5,00 L contenente 10,0 g di iodio è caricato con 10,0 g di fluoro. Al
termine della reazione, la temperatura nel pallone è pari a 125 °C. calcolare a) la
pressione parziale, b) la frazione molare del pentafluoruro nel pallone e c) la pressione
totale nel pallone.
I2
F2
IF5
Massa (g)
10,0
10,0
PM (g mol-1)
253,8
38,00
Moli iniziali (mol)
0,04
0,26
Moli reagite (mol)
-0,04
-0,20
+0,08
Moli finali (mol)
-
0,06
0,08
a)
Pi = niRT/V
P(IF5) = n(IF5)×RT/V
P(IF5) = (0,08 × 0,082 × 398,15)/5 = 0,52 atm
b)
χ(IF5) = n(IF5)/nTOT = n(IF5)/[n(IF5) + n(F2)]
χ(IF5) = 0,08/(0,08 + 0,06) = 0,57
c)
PTOT = nTOTRT/V
PTOT = [(0,08 + 0,06) × 0,082 × 398,15]/5 = 0,91 atm
Oppure
PTOT = Σi Pi
PTOT = P(IF5) + P(F2) = P(IF5) + n(F2)×RT/V
Es.
Es. 8: L’aria contiene il 20,95% in volume di ossigeno (O2). Calcolare il volume di aria
necessario a 25 °C a 1 atm per la combustione totale di 1,00 L di etere dietilico
(C4H10O, densità 0,7134 g/mL) secondo la reazione:
C4H10O + 6 O2 → 4 CO2 + 5 H2O
V(aria) = V(O2) × 100/20,95
V(O2) = n(O2) × RT/P
n(O2) = 6 × n(etere) = 6 × m(etere)/PM(etere) = 6 × d(etere) × V(etere) / PM(etere)
V(O2) = [6×d(etere)×V(etere)/PM(etere)]×RT/P = [6×d(etere)×V(etere)×RT]/[PM(etere)×P]
V(O2) = (6× 0,7134×103 × 1 × 0,082 × 298,15)/(74,50 × 1) = 1405 L = 1,405 m3
V(aria) = (1,405 × 100)/20,95 = 6,706 m3
La Teoria Cinetica Dei Gas
Modello del comportamento dei gas a livello molecolare, sviluppato in ca. 100
anni, arrivato a compimento nel 1857 ad opera di Rudolf Clausius (1822-1888).
Si basa sulle seguenti assunzioni:
I gas sono costituiti da ‘particelle’ (atomi o molecole) che si muovono in modo
continuo e casuale.
Il volume totale delle ‘particelle’ è trascurabile rispetto al volume occupato
complessivamente dal gas.
Le ‘particelle’ sono indipendenti le une rispetto alle altre: le forze attrattive e
repulsive reciproche sono trascurabili.
Le ‘particelle’ collidono. Le collisioni possono comportare trasferimento di una
certa quantità di energia da una ‘particella’ ad un’altra. Tuttavia, l’energia
cinetica media dell’intero gas non cambia.
L’energia cinetica media delle ‘particelle’ è proporzionale alla temperatura
assoluta. A una data temperatura, le ‘particelle’ di qualunque gas hanno la
stessa energia cinetica media.
La teoria cinetica lega pressione e temperatura al comportamento delle ‘particelle’.
La pressione di un gas è il risultato delle collisioni delle sue
‘particelle’ contro le pareti del contenitore, e dipende sia dalla
forza, sia dalla frequenza con cui si verificano le collisioni.
La temperatura assoluta di un gas è la misura dell’energia cinetica media
(Ecin(av)) delle sue ‘particelle’.
Le ‘particelle’ di un gas hanno la stessa Ecin(av) e la stessa velocità media, MA
ognuna ha uno specifico valore di energia e di velocità, distribuite secondo una
distribuzione Maxwelliana (come già le ‘particelle’ di un liquido):
ump = velocità più probabile = velocità della maggior parte
delle ‘particelle’
uav = velocità media
urms = velocità quadratica media = velocità di una ‘particella’
con energia cinetica pari a Ecin(av): Ecin(av) = ½ m (urms)2
Quanto maggiore è la temperatura del gas, tanto più la
distribuzione si sposta verso destra. La velocità più
probabile, la velocità media e la velocità quadratica
media aumentano. A 0 °C (curva blu), meno della metà
delle particelle si muove con velocità maggiore di 500
m/s. A 100 °C, più della metà delle particelle si muove
con velocità superiore a tale valore.
EFFETTO DELL’AUMENTO DI VOLUME A TEMPERATURA COSTANTE (legge di
Boyle): In termini di teoria cinetica dei gas, temperatura costante implica energia
cinetica media costante, ovvero velocità quadratica media costante. Se il volume
aumenta, le particelle devono percorrere una lunghezza maggiore tra due
collisioni. Le collisioni sono meno frequenti e la pressione del gas è minore.
EFFETTO DELL’AUMENTO DI TEMPERATURA A VOLUME COSTANTE: In
termini di teoria cinetica dei gas, aumento di temperatura implica aumento di
energia cinetica media e di velocità quadratica media. Cresce la frequenza delle
collisioni, i.e. la pressione del gas.
EFFETTO DELL’AUMENTO DI TEMPERATURA A PRESSIONE COSTANTE
(legge di Charles): In termini di teoria cinetica dei gas, aumento di temperatura
implica aumento di energia cinetica media e di velocità quadratica media. Cresce
la mobilità delle particelle, le distanze percorse, il volume da esse occupato.
T = 25 °C
EFFETTO DELLA
MASSA MOLARE A
TEMPERATURA COSTANTE: L’energia cinetica
media di gas diversi alla stessa temperatura è
la stessa, Ecin(av) = ½ m (urms)2. Quanto
maggiore è la massa molare (PM) di
un gas, tanto minore è la sua velocità quadratica media, ovvero tanto più è
spostata a sinistra la distribuzione delle velocità. Quantitativamente:
urms = (3RT/PM)½
La velocità più probabile è invece pari a:
ump = (2RT/PM)½
I Gas Reali
L’equazione di stato dei gas ideali è un modello molto utile, ma non sempre
rispettato dai gas reali. Riprendiamo l’equazione PV/RT = n. Per n = 1, PV/RT =
1. Per gas reali, si verifica sperimentalmente che, quanto più elevata è la
pressione, tanto più il rapporto PV/RT si discosta da 1:
La deviazione da PV/RT = 1 è
grande e specifica per ogni gas.
I gas reali non si comportano idealmente ad alte pressioni. Al di sotto delle 10
atm, la deviazione dall’idealità è contenuta ed è possibile utilizzare l’equazione
di stato dei gas ideali.
Ovviamente, la deviazione dall’idealità dipende anche dalla temperatura:
Comportamento di N2
La deviazione da PV/RT = 1 è tanto
maggiore
quanto
più
bassa
è
la
temperatura, e diventa molto significativa in
prossimità
condensazione.
della
temperatura
di
I Gas Reali: l’Equazione di van der Waals
Lo scienziato olandese Johannes van der Waals (1837-1923) propose una
equazione per predire il comportamento dei gas reali. Partì dall’equazione di
stato dei gas ideali e introdusse 2 fattori correttivi (a, b – detti COSTANTI DI
VAN DER WAALS) che tenessero in considerazione le attrazioni tra le ‘particelle’
e il loro volume finito. Ne scaturì l’EQUAZIONE DI VAN DER WAALS:
(P + an2/V2)(V - nb) = nRT.
a è una misura dell’attrazione reciproca tra le ‘particelle’: il fattore an2/V2
aumenta la pressione reale del gas (diminuita in ragione delle attrazioni
reciproche) per portarla al valore ideale. Le forze attrattive tra ‘particelle’ sono
direttamente proporzionali al quadrato del numero di ‘particelle’ per unità di
volume (i.e. n2/V2)
b è una misura del volume finito occupato dalle ‘particelle’:
viene sottratto per portare il volume al valore ideale.
il fattore nb
Costanti di van der Waals di alcuni gas
Le costanti di van der Waals sono valori determinati sperimentalmente che
differiscono da gas a gas. Dalla tabella si evince che le costanti aumentano
all’aumentare della massa molare: le molecole a massa molare maggiore
occupano un volume effettivo maggiore e danno luogo a interazioni più
energetiche.