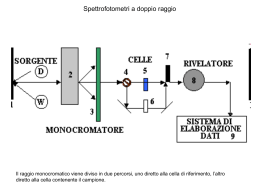
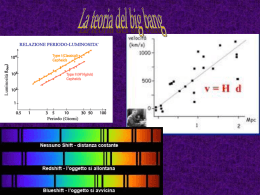
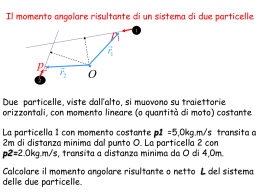
Fisica moderna
A. Palano
Testi di riferimento:
P.J. Nolan, Complementi di Fisica, fisica moderna
Halliday, Resnick, Krane, Fisica 2
La radiazione di corpo nero
•
•
Primo indizio che la teoria classica e' inadeguata a descrivere alcuni fenomeni.
Riscaldando un oggetto questo emette radiazione. Spettro continuo.
Sole
•
: emettenza energetica spettrale: flusso di energia emesso nell'unita' di tempo per unita' di superficie per intervallo di
lunghezza d'onda. Si esprime in
.
•
•
Caratteristiche di emissione e di assorbimento simili.
Un corpo che assorba tutte le radiazioni e' detto corpo nero. Si puo' simulare con una scatola con un foro.
•
•
Analogamente un corpo nero riscaldato emette piu' radiazione di qualunque altro corpo.
Tentativo di spiegare la radiazione di corpo nero da parte di Rayleigh. Cavita' come sede di onde stazionarie.
Radiazione di corpo nero
•
Utilizzo dell'equipartizione dell'energia. Ciascuna delle onde doveva avere un valore
•
•
Spettro ottenuto in disaccordo per piccoli valori di
: energia infinita.
Idea di Planck. Quantizzazione dell'energia. Energia degli oscillatori quantizzata secondo la sequenza:
•
Per n=1 otteniamo il valore piu' piccolo, pari a:
•
•
Inibizione degli oscillatori ad alta frequenza.
Legge di Wien, valore massimo della distribuzione:
•
La legge di distribuzione ottenuta e':
Radiazione di corpo nero
•
Integrando si ottiene:
•
Legge di Stefan-Boltzmann.
L’effetto fotoelettrico
•
Quando la luce colpisce una superficie metallica questa emette elettroni. L'emissione e' immediata.
•
Diminuendo la tensione diminuisce la corrente. Quando V=0,
si invertono le polarita' e la corrente continua a decrescere. Se
aumenta l'intensita' luminosa si ha una seconda curva.
•
Si ottiene quindi una proporzionalita' fra corrente e intensita'
luminosa:
•
potenziale di arresto. Indipendente dall'intensita' luminosa.
•
Quando il potenziale e' invertito, gli elettroni possono giungere
sull'anodo solo se possiedono un'energia cinetica superiore a:
•
dove e e' la carica dell'elettrone.
•
Se si cambia la frequenza della luce, cambia anche
una proporzionalita' del tipo:
•
Esiste una frequenza di soglia
, attraverso
, sotto la quale non vi e' effetto fotoelettrico.
Effetto fotoelettrico
•
•
•
La teoria classica non riesce a predire questi risultati. In particolare non ci si aspetterebbe una frequenza di
soglia ne' una dipendenza di
dalla frequenza.
Teoria di Einstein.
Energia non distribuita uniformemente sul fronte d'onda ma quantizzata in particelle: fotoni. Energia:
•
Il fotone viene assorbito dall'elettrone che utilizza una parte dell'energia
per vincere il lavoro di estrazione dal solido,
. Quindi:
•
Se il flusso di corrente si annulla,
soglia. Quindi:
e
•
Infine:
•
Cio' spiega l'esistenza di una frequenza di soglia.
, la frequenza di
La massa del fotone
•
Secondo la relativita', la massa di una particella e' data da:
•
•
•
Se la sua velocita' e' quella della luce allora,
.
L'unico modo di ovviare a questo problema e' quello di porre
.
Tuttavia si puo' determinare la massa associata ad un fotone dalla relazione:
•
Poiche':
•
e quindi:
•
Dall'equazione:
•
elevando al quadrato:
•
Moltiplicando per
•
Che si puo' scrivere come:
•
La quantita' di moto di una particella e' quindi:
La massa del fotone
•
Dove
•
Per la luce
•
Abbiamo anche
•
Poiche':
•
La luce si propaga attraverso fotoni. A queste particelle e' associata una lunghezza d'onda :
•
Principio di corrispondenza. Per descrivere il comportamento di questi oggetti occorre tener conto degli
effetti corpuscolari e ondulatori.
e quindi la quantita' di moto del fotone e':
, quindi:
Effetto Compton
•
Effetto Compton: Interazione di un fotone con un elettrone. Il fotone cambia la sua
frequenza. Trattato come un urto elastico fra particelle in cui si conservano
l'energia e la quantita' di moto.
Onde di materia
•
•
Natura ondulatoria delle particelle.
De Broglie e l'ipotesi che alle particelle sia associata un'onda.
•
Dualismo onda-corpuscolo esteso dal fotone a tutte le particelle.
• Onde associate alla materia come onde di probabilita'.
• Il principio di indeterminazione di Heisenberg.
• Per un'onda di estensione infinita,
e' univocamente
determinato.
•
•
La particella si puo' trovare in qualunque posizione.
Pacchetto d'onde largo
. Diversi numeri d'onda. Possiamo scrivere:
•
dove:
Principio di indeterminazione
•
Se associamo questa distribuzione ad una particella, possiamo utilizzare l'equazione di de Broglie:
•
Differenziando:
•
Quindi
•
Ovvero:
•
Dove
•
Non e’ possibile avere simultaneamente
misure precise della posizione della quantita’ di moto.
•
Onde e particelle.
Verifiche sperimentali
•
Diffrazione degli elettroni (particelle) simile a qualle dei raggi X (onde)
Particelle virtuali
•
Un'altra forma del principio di indeterminazione e:
•
•
Particelle virtuali.
E' possibile una violazione della conservazione dell'energia per un tempo:
•
Tenendo presente che:
•
La particella virtuale si puo' al massimo allontanare fino ad una distanza pari a:
•
•
Nell'ipotesi che la particella sia un protone e che venga emesso un pione (
Allora:
•
La distanza e' quindi:
•
•
Raggio del nucleo di idrogeno:
, uranio :
: mesone di Yukawa, scoperto effettivamente nel 1947.
).
Interazioni come scambio di particelle virtuali
•
Scambio di pioni fra protoni.
L’atomo di Idrogeno
•
•
Una particella carica accelerata emette radiazione elettromagnetica. Un elettrone che ruota attorno al
nucleo si muove di moto accelerato per cui dovrebbe perdere energia e cadere nel nucleo.
Teoria dell'atomo di Bohr. L'elettrone puo' ruotare solo su orbite in cui il momento angolare e' quantizzato:
dove n e' il numero quantico principale, n=1,2,3,...
•
Si puo' giungere allo stesso risultato utilizzando le onde di de Broglie, assumendo che queste formino delle
onde stazionarie.
•
Otteniamo:
•
Da cui:
•
•
Calcoliamo ora il raggio delle orbite.
Dalla seconda legge di Newton:
•
dove F e' la forza elettrica e a l'accelerazione centripeta:
•
Dalla (1):
L’atomo di idrogeno
•
Quindi:
•
•
Quindi le orbite sono quantizzate.
Sostituendo
possiamo scrivere per la velocita':
•
Energia associata ad ogni orbita:
•
Quindi:
L’atomo di idrogeno
•
Se definiamo lo stato fondamentale come:
•
Allora:
•
•
Spettri atomici.
Se un elettrone passa da un'orbita all'altra, viene emesso un fotone:
•
La frequenza e' quindi:
•
Atomo di Bohr solo approssimato. Presenza di righe spettrali non
previste dal modello.
Meccanica quantistica
•
Equazione d'onda di Schrodinger per una singola particella di massa m lungo una sola dimensione:
•
In presenza di un potenziale V(r):
•
Significato fisico di
•
Calcolo dello stato fondamentale dell’atomo di idrogeno
, densita' di probabilita':
L’atomo di idrogeno
•
•
L'atomo di idrogeno in meccanica quantistica. Occorrono 3 numeri quantici.
a) Numero quantico principale n, che e' lo stesso dell'atomo di Bohr:
•
b) La quantizzazione di L segue la legge:
•
Il numero quantico orbitale l che puo' assumere soltanto i valori:
•
c) Numero quantico magnetico. E' quantizzata la proiezione di L lungo l'asse di rotazione.
•
dove
puo' assumere solo i valori:
L’atomo di idrogeno
•
•
Spin dell'elettrone.
All'elettrone e' associato un momento angolare di spin:
•
Analogamente al momento angolare, lo spin e' quantizzato:
•
La componente z dello spin e' quantizzata e puo' solo assumere valori:
•
•
L'elettrone non e' una sfera rotante.
Se lo fosse avremmo:
•
Segue che, poiche‘
•
maggiore di quella della luce.
•
Principio di esclusione di Pauli. Due elettroni non possono avere lo stesso set di numeri quantici.
la velocita' con cui ruota la superficie e'
L’atomo di idrogeno
•
Orbitali atomici. Stato 2S.
•
Stato 2P.
Il sistema periodico
•
La tavola periodica degli elementi
Sezione d’urto
•
Le collisioni sono lo strumento fondamentale con cui la Fisica ha esplorato la struttura interna della materia. La
quantita' che fornisce le informazioni necessarie sulle dimensioni dei bersagli che vogliamo studiare e' la sezione
d'urto.
•
Nella figura e' schematizzato uno strato di materiale contenente atomi, rappresentati da sfere. Su questi atomi
vengono lanciati dei proiettili, in modo uniforme, su tutta la superficie del materiale che chiameremo A.
Supponiamo che lo spessore del materiale che stiamo esaminando sia s e che questo contenga un numero M di
bersagli.
•
Supponiamo che sia
il numero di proiettili lanciati in un certo intervallo di tempo e sia N il numero di
proiettili che colpisca un bersaglio.
•
Possiamo allora scrivere che la frazione di proiettili che colpisce il bersaglio deve essere uguale alla frazione di area
occupata dai bersagli:
•
dove abbiamo indicato con
d'urto.
Dalla (1) otteniamo:
•
la quantita' che ci interessa misurare, l'area di ciascun bersaglio ovvero la sezione
•
Trasformiamo ora queste variabili in quantita' meglio misurabili come il numero di atomi/bersagli per unita' di
volume:
•
quindi:
•
e quindi la (2) diviene:
L’esperimento di Rutherford
•
Per esemplificare, consideriamo qui il metodo con cui si e' giunti a comprendere la struttura dell'atomo e a
misurarne le dimensioni: l'esperimento di Rutherford.
•
In questo esperimento su utilizzo' una lamina di oro di spessore s=4
atomi per
n=5.9
.
•
Vi erano due teorie sull'atomo. Nella prima (modello di Thomson) si sosteneva che la materia atomica
fosse distribuita uniformemente all'interno di una sfera, nella seconda (Rutherford) si supponeva che essa
fosse concentrata in un nucleo di piccole dimensioni.
•
•
m contenente un numero di
Per studiare questo problema si utilizzarono come proiettili particelle provenienti dal decadimento
radioattivo del Polonio.
•
Se l'atomo avesse tutta la materia distribuita uniformemente le particelle avrebbero interagito con gli
atomi e sarebbero state deviate di angoli piccoli. Se invece la materia fosse stata concentrata in un nucleo
piccolo, la probabilita' di interazione sarebbe stata piu' piccola ma alcune particelle avrebbero colpito
questi nuclei e sarebbero state spinte all'indietro.
•
Le cose andarono proprio in questi termini e Rutherford misuro' un numero di particelle che andavano
all'indietro di:
•
Con queste informazioni possiamo calcolare la sezione d'urto e quindi le dimensioni dei nuclei.
•
Supponendo che il nucleo abbia una forma sferica (
), possiamo ottenere il raggio nucleare:
Il nucleo dell’atomo
•
La radiattivita'. Particelle
,
e
.
•
•
•
Nucleo: protoni e neutroni.
Numero atomico: Z. Numero di massa A.
Numero di neutroni: N.
•
Simboli:
•
Ad esempio:
•
•
Isotopi: nuclei aventi lo stesso Z ma diverso A (e quindi N).
Ad esempio:
•
Diverse abbondanze degli isotopi.
Difetto di massa
•
Forza di interazione forte e elettromagnetica. L'interazione forte a corto range, quella elettromagnetica a
range infinito. La forza nucleare non distingue fra protoni e
neutroni
•
Difetto di massa:
•
Energia di legame:
•
Energia di legame per nucleone:
•
I nuclei della regione centrale sono impacchettati con piu' alta energia. Quindi si puo' liberare energia agli
estremi della curva.
Decadimento radioattivo
•
•
Legge del decadimento radiattivo. Il numero di nuclei che disintegrano in un tempo
al numero di nuclei presenti
costante di disintegrazione.
•
Tempo di dimezzamento: il tempo in cui il numero di nucleoni si dimezza.
•
Vita media:
e' proporzionale
Decadimento
•
Particella
•
Esempio:
:2 protoni + 2 neutroni.
•
Tempo di dimezzamento di 4.51
a.
•
Effetto tunnel.
•
Decadimento in due corpi. Legge di conservazione della quantita’
di moto.
•
Energia di disintegrazione:
•
La velocita’ v1 vale:
•
•
Per una specie chimica la velocita’ e’ sempre la stessa.
Figura.
Decadimento
•
•
Decadimento
. Emissione di un elettrone negativo.
A livello del nucleone (permessa anche fuori dal nucleo poiche' il n ha una massa maggiore del p):
•
Esempio:
•
•
Tempo di dimezzamento: 24 d.
Decadimento in tre corpi, presenza del neutrino. Energia cinetica dell’elettrone continua.
•
•
Decadimento
. Emissione di un elettrone positivo.
A livello del nucleone (non possibile al di fuori del nucleo):
•
Ad esempio:
•
Tempo di dimezzamento: 7.4
a.
Decadimento
•
Esempio:
•
Catene di decadimento.
Reazioni nucleari
•
Reazioni endotermiche e esotermiche.
•
La fissione nucleare.
•
•
I frammenti y e Y hanno Z compreso fra 36 e 60.
Esempio:
•
Reazioni esotermiche.
•
Modello a goccia.
•
Reazioni a catena. Il numero di n prodotti
e' maggiore di quelli incidenti.
Reazioni nucleari
•
•
•
•
•
Uranio naturale contiene il 99.3 % di
catena.
Uranio per ordigni nucleari: 50 %
.
Uranio per reattori nucleari: 3.6 %
.
Bomba atomica: massa critica.
Uso del Plutonio, piu' facile da produrre.
e solo lo 0.7 % di
che puo' dare una reazione a
•
Reattore nucleare.
•
Uranio in acqua. L'acqua rallenta i neutroni veloci perche’
inneschino la reazione nucleare, moderatore.
•
La reazione e' controllata da barre di cadmio che e' in grado di assorbire neutroni senza diventare
instabile.
•
Energia liberata pari a circa 2.5 milioni di volte
di quella di un equivalente reazione chimica.
La fusione nucleare
•
Catena di reazioni nel Sole.
•
Totale:
•
•
Il Q totale e' di 26 MeV. Temperatura:
La bomba all'idrogeno.
•
•
•
Il trizio e' prodotto nelle reazioni nucleari.
Una bomba al Plutonio innesca la reazione.
Reattori nucleari a fusione.
.
Le forze fondamentali della natura
•
•
•
La forza forte: energia nucleare. Il sole.
Intensita’: 1
Range:
m
•
•
•
La forza elettromagnetica: atomi, molecole
Intensita’: 1/137.
Range:
•
•
•
La forza debole: radiattivita’
Intensita’:
Range:
•
•
•
La forza di gravita’: galassie
Intensita’:
Range:
Particelle e antiparticelle
•
•
1928, P. Dirac. Teoria relativistica dell'elettrone. Simmetria materia-antimateria.
Conversione energia massa:
•
•
•
•
Antiparticelle. Stessa massa, carica opposta.
Identiche dal punto di vista delle leggi della fisica.
Anti-atomi con antiprotoni e positroni.
Nel Big-Bang si produsse tanta materia che antimateria.
•
•
•
Sacharov: tenue differenza fra materia e antimateria.
Osservata nei decadimenti dei K0
Osservata nei decadimenti dei B0
http://www.particleadventure.org/
Materia e antimateria
•
•
For every type of matter particle we've found, there also exists a corresponding antimatter
particle, or antiparticle.
When a matter particle and antimatter particle meet, they annihilate into pure energy!
We are lucky because…
Immediately after the Big Bang, the matter and antimatter… were not exactly equal
10,000,000,001
10,000,000,000
Antimatter
The Great Annihilation followed
Matter
us
1
Matter
Antimatter
All the antimatter, and all but a tiny part of the matter were gone… and that tiny part is
us.
37
L’espansione dell’universo
•
Spostamento verso il rosso per una galassia.
•
Righe di assorbimento del Calcio. Righe di emissione nel
laboratorio. Velocita’: 21 000 Km/sec.
•
Legge di Hubble:
v=Hd
1Mpc = 3.26 M anni luce = 3.084 1019 Km
•
Se l’universo si sta espandendo sempre con lo stesso rate,
eta’ dell’universo:
Fra 12 e 16 miliardi di anni.
La radiazione fossile di microonde.
•
3) Microonde. Onde radio molto corte, fra 1 mm e 1 m. Oscillatori elettromagnetici in circuiti elettrici. Utilizzate in
trasmissioni telefoniche. L'universo e' completamente riempito da microonde residuo del big bang.
•
Molte delle grandi scoperte scientifiche sono avvenute per caso: così è stato anche per la cosiddetta radiazione di fondo a 3
K (o radiazione fossile a microonde), individuata nel 1965 da due fisici americani della Bell Telephone Company (la società
privata dei telefoni).
•
La società dei telefoni americana agli inizi degli anni sessanta aveva ingaggiato due giovani fisici, Arno Allan Penzias e
Robert Woodrow Wilson, con il compito di rendere operativa una grande antenna “a corno” per la ricezione di onde radio
provenienti dal primo satellite per telecomunicazioni messo in orbita intorno alla Terra, l’Echo. Si trattava, in particolare, di
studiare la sensibilità dello specchio e del ricevitore di questa antenna, la quale stranamente produceva un fastidioso ronzio
che i due ricercatori, in un primo momento, pensarono fosse dovuto alla presenza in zona di qualche radio trasmittente. Il
ronzio era causato da onde elettromagnetiche della lunghezza di 7,35 cm, ma le ricerche accertarono che nei dintorni non vi
era alcuna trasmittente che operasse su quella lunghezza d’onda. Inoltre, poiché la radiazione era del tutto analoga a quella
emessa da un corpo freddo, si pensò anche di rimuovere i rifiuti organici che alcuni piccioni avevano depositato all’interno
dell’antenna in cui avevano trovato dimora, perché potevano essere proprio quegli escrementi a produrre il fruscio
indesiderato.
•
Il ronzio di fondo, nonostante tutte le ricerche delle cause e i tentativi di eliminarlo, rimaneva ed era del tutto
indipendente dall’orientazione dell’antenna: proveniva cioè da tutte le direzioni e con la stessa intensità. I due giovani
radioastronomi, incuriositi e interessati al fenomeno, ne parlarono con alcuni colleghi che li consigliarono di rivolgersi alla
vicina Università di Princeton dove si trovavano due fisici, Robert Dicke e James Peebles i quali stavano progettando una
strumentazione adeguata per tentare di captare una radiazione che, secondo le previsioni dell’astronomo George Gamow,
avrebbe dovuto permeare di sé tutto l’Universo.
•
Gamow è lo scienziato che nel 1948 aveva avanzato l’idea che l’Universo fosse il risultato di una tremenda esplosione (il
notissimo Big Bang) la quale, come tutte le esplosioni, oltre a lanciare materia tutto intorno, avrebbe anche generato grandi
quantità di energia. Secondo questo modello la palla di fuoco primordiale, costituita da una miscela di radiazione e materia
ad altissima temperatura, iniziò ad espandersi e, insieme con l’espansione, si dilatò anche la radiazione elettromagnetica, la
quale è contraddistinta da onde di diversa lunghezza a seconda dell’energia che trasporta. Le onde elettromagnetiche che
caratterizzavano la radiazione dell’Universo nei suoi primi istanti di vita dovevano essere cortissime, ma l’espansione le rese
più lunghe.
39
Lo spettro elettromagnetico
•
•
•
Le moderne teorie sulla composizione della materia suggeriscono quindi che l’Universo all’inizio dei tempi fosse molto
diverso da quello a noi familiare. Finché la temperatura rimase su valori molto elevati, i nuclei e gli elettroni non erano in
grado di unirsi per formare atomi stabili: la materia per un certo tempo si presentò quindi sotto forma di plasma, cioè di
particelle cariche di elettricità libere di muoversi e in continua interazione con la radiazione la quale, rimbalzando fra una
particella e l’altra, si trovava intrappolata all’interno dei costituenti sciolti degli atomi. Però quando finalmente dopo circa
500.000 anni dal “bang” iniziale la temperatura, scesa al di sotto di alcune migliaia di gradi, consentì la formazione dei primi
atomi stabili, la radiazione si svincolò dalla materia e cominciò a viaggiare liberamente nello spazio.
Frattanto la materia che costituiva l'Universo primordiale, in seguito all'espansione, si diradò molto velocemente e la
radiazione da essa emessa aumentò progressivamente la sua lunghezza d'onda, fino a raggiungere quella attuale di alcuni
centimetri. Una radiazione elettromagnetica con l'onda di alcuni centimetri è un'onda radio e corrisponde a quella che
emergerebbe da un corpo che si trovasse alla temperatura di 3 K, cioè a 270 °C sotto zero.
Per analogia con i fossili animali e vegetali che sono il residuo di ciò che erano questi organismi originariamente, la
radiazione proveniente dal fondo dell'Universo viene anche chiamata «radiazione fossile».
40
Le particelle elementari
•
Prima classificazione delle particelle.
•
•
Leptoni. Interazione debole ed elettromagnetica. Diametro minore di
Spin:
•
Masse:
•
Vita media:
m.
Gli adroni
•
•
•
Interagiscono mediante la forza forte.
Gell-Mann e Zweig: i quarks. Particelle di spin
degli adroni.
Confinamento.
con carica elettrica frazionaria confinate all'interno
Adroni
Spettri mesoni leggeri con quarks u,d,s. spin 0 e 1
La carica di colore e la forza forte.
•
•
•
•
I quarks hanno una carica di colore.
Interazione mediante gluoni.
L’interno di un protone.
Forza nucleare come forza residua.
La forza debole
•
•
•
•
Responsabile dei decadimenti radioattivi.
Particelle W e Z mediatori della forza debole.
Masse: 80 e 91 GeV.
Forza debole a range cortissimo.
Acceleratori di particelle.
Piu’ alta l’energia degli acceleratori, piu’ si
va indietro nel tempo nella vita dell’universo, quando
si formarono protoni, nuclei e atomi.
Gli acceleratori come Large Hadron Collider
(LHC) e il futuro Linear Collider (ILC) sono
come telescopi che guardano i primi istanti di vita
dell’universo
LHC
L’ unificazione delle forze
Alla scala delle energie che noi vediamo le 4 forze fondamentali
sono distinte.
Alla scala di LHC e ILC le forze Elettromagnetiche e Deboli si
unificano.
Potremo quindi avere informazioni sulla grande unificazione
delle forze.
go here
sense whats happening here
Le grandi domande sull’Universo.
I. Il sogno di Einstein
1.
Nuove Leggi della Fisica?
2. Energia scura?
3. Altre dimensioni spaziali?
II. Il mondo delle
particelle
4. Unificazione delle forze?
5. Nuove particelle?
6. Materia scura?
III. La nascita
dell’universo
7. Cosa sono I
neutrini?
8. Come nacque
l’Universo?
9. Dove si trova
l’antimateria?
Both Matter and Antimatter have Mass
But what was the origin of that mass?
What gives masses to fundamental particles such as
quarks and electrons
and why are they so different?
49
Higgs Boson
To understand how the Higgs
works,
imagine that a room full of
physicists chattering quietly is
like space filled with the Higgs
field ...
50
Higgs Boson
... a well-known scientist walks in, creating a
disturbance as he moves across the room
and attracting a cluster of admirers with
each step ...
... this increases his resistance to
movement, in other words, he
acquires mass, just like a particle
moving through the Higgs field...
-- Prof. David Miller
51
Cosa sono materia ed energia scure?
Much Evidence for its Existence
In galaxies and galaxy clusters
There is not
enough visible
mass in rotating
spiral galaxies to
hold them
together
Separation of
dark matter and
ordinary matter
in the collision
of two clusters
of galaxies
Photos courtesy of NASA
53
Is Matter also in Other Dimensions?
Are there extra dimensions of space that we cannot see?
(Dali, The Disintegration of the Persistence of Memory, 1954)
54
How can there be extra dimensions?
Think about an acrobat and a flea on a tight rope.
The acrobat can move forward and backward along the rope.
But the flea can also move sideways around the rope.
If the flea keeps walking to one side, it goes around the rope
and winds up where it started.
55
How can there be extra dimensions?
So the acrobat has one dimension, and the flea has two dimensions, but one
of these dimensions is a small closed loop.
The acrobat can only detect the one dimension of the rope,
just as we can only see the world in three dimensions,
even though it might well have more.
This is impossible to visualize, precisely because we can only visualize things in
three dimensions!
56
Il mistero dei neutrini.
• A che servono 3 neutrini?
• Esperimenti con neutrini. Si creano neutrini di un tipo
in un acceleratore e si rivelano a grandi distanze dove
si trasformano in un’altro tipo.
MINOS
Opera