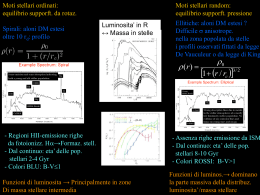

 = pitch angle
 = pitch angle
Sa
Sc
• Bulge molto prominente
• Bulge poco prominente
• Bracci molto avvolti
Flocculent
Spiral
• Bracci
poco avvolti
• Bracci poco risolti
• Bracci molto risolti
La dispersione di velocita’ s misura
il moto random
Ellittiche:
Sostenute
Indica la larghezza
della distribuzione
dal moto
di velocita’
random,
Non dal
moto
rotazionale
ordinato
Distribuzione delle velocita’ stellari al
Centro di una galassia ellittica
Il “twist” delle isofote è una prova della triassialità delle galassie ellittiche.

2
tot
     
2
r
2
 r2   2   z2
2
z
Rotazione
Anisotropie di velocita’
Sovrapposizione di
orbite molto complesse
Le ellittiche hanno
spesso anche una
rotazione, in particolare
nelle regioni esterne
GM (r )

v 
r
r
r
2
c
Zona interna: vc cresce circa
linearmente (rotazione rigida,
densita’ costante)
2
M (r ) 
1
r 
 vbr  rdr
G  rbr 
dM 4 2
3  vbr 
    0

r dr (r )   
dr
3
4G  rbr 
Zone esterne: vc rimane piatta
1 2
dM (r )  v flatdr  4  (r ) r 2 dr
G
v 2flat 1
 (r ) 
4 G r 2
Profilo isotermo
(a grandi distanze dal centro)
3  vbr 
 
0 
4G  rbr 
Per r e vc solari, 1 massa del protone per cm3
- Cosa causa l'appiattimento in ellittiche da E0 a E7? (moti rotaz. o anisotropia dei moti random)
- Stime dinamiche di massa delle galassie ellittiche: massa oscura in galassie ellittiche
- Profilo di massa per galassie ellittiche
Orbite:
1)
Tempo di rilassamento e campo medio
2)
Orbite in potenziali pre-assegnati
3)
Orbite in simm assiale, epicicli
4)
freq. di Lindblad, struttura a spirale
5)
Orbite in potenziali non-simm. e 3D
Equilibrio
1)
Teorema di Boltzmann
2)
Equazione di Jeans
3)
Teorema di Jeans e teorema del viriale
4)
Equilibrio Idrostatico
5)
Applicazioni: - misura profili di massa
in galassie ellittiche e ammassi
- misura di masse con il teorema del viriale
dark matter in ammassi di galassie
- profili di densita’ di sistemi non collisionali
- Cosa orgina i bracci a spirale e le loro proprieta’
Profili di brilanza superficiale
Leggi empiriche
Ellittiche e Bulges centrali delle spirali
I (r )  I e e
 7.67[ ( r re )
1
4 -1]
de Vaucouleur s
Dischi delle spirali
(mediati in cerchi per eliminare la struttura a spirale)
I (r )  I 0 e ( r
I(0) = brillanza superficiale centrale
r0 = lunghezza di scala
r0 )
Schweizer
r0 varia da galassia a galassia
I0 piccola variazione
21.65 +/- 0.3 mag/arcsec2 in the B band (Freeman 1970).
I e’ definita come la densita’ di flusso per unita’ di angolo solido
Per distanze non cosmologiche e’ indipendente dalla distanza della sorgente:
L
r
F  2 ma  
d
d
L 2 1
L
I 2 2  2
r 
r
Profili apparenti e profili deproiettati
In generale per’ il sistema non é ‘’a priori’’ a simmetria sferica
King
De Vaucouleurs
Confronto tra la legge di King e la legge r1/4
Spettri Tipici
righe in emissione caratteristiche di regioni HII
Il gas ionizzato produce forti righe di emissione
Gli elettroni liberi si ricombinano temporaneamente
ed emettono un fotone prima che l’atomo sia
nuovamentre ionizzato
Se la formazione stellare si ferma
le stelle O scompaiono in pochi Myr
Le altre stelle non ionizzano
efficientemente il gas
Ha scompare
Ellittiche: B-V>1; -22<MV<-18
Spirali: B-V≈1 (Bulge B-V>1); -21<MV<-17
Irregolari: B-V< 0.8; -18<MV<-10
Luminosita’ della componente di stelle
giovani (in verticale) ed evolute
(orizzontale) per i vari tipi morfologici
delle galassie.
Morfologia
La classificazione morfologica delle
galassie
25 % Ellittica
75 % Spirale (con o senza barre)
1 % Irregolare
a
0  L 
  exp(  L / L* )
 ( L) 
L*  L* 
0 ≈ 10-2 Mpc-2
normalizzazione
L* ≈ 4 1010 Lʘ
Lum. caratterstica
E
S0/a/b
a≈ -1.1
Pendenza a basse lumin.
Sc/d
Irr
AAT 2dF fibre positioner
Misura simultaneamente fino a 400 redshifts
Funzioni di Luminosita’ in banda R