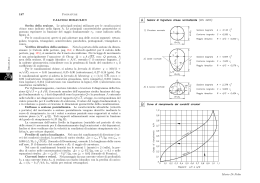
appendice A
Esempio di progetto geometrico
Pagina 29 del testo
A.1 Progetto di un tratto stradale
In questa sezione sono descritti i passi successivi del processo di progettazione di un tracciato stradale, seguendo l’approccio semplificato di stampo
tradizionale. Tale metodologia, ancorché attualmente superata, o↵re una rappresentazione di base delle varie fasi progettuali, analizzando la struttura e la
tipologia degli elaborati da produrre.
Si suppone di dover progettare una strada extraurbana secondaria di Categoria C, a unica carreggiata e doppio senso di marcia, avente intervallo di
velocità di progetto 60-100 km/h.
Andamento planimetrico
Step 1. Costruzione del tracciolino
L’andamento planimetrico della strada viene progettato facendo riferimento a
una planimetria in scala 1 : 2000; su tale planimetria sono tracciate le isoipse,
o curve di livello, caratterizzate da una quota costante e riferita al livello
del mare. Il primo passo prevede l’individuazione del cosiddetto tracciolino,
costituito da una poligonale a pendenza costante, che collega le due estremità
del tracciato.
Noto il dislivello che separa i punti estremi da collegare, si può calcolare una
pendenza media di riferimento. Per la costruzione del tracciolino è conveniente assumere una pendenza (p) leggermente inferiore sia alla pendenza media
calcolata sia al limite previsto dalle norme per il tipo di strada in progetto.
Considerando due curve di livello con equidistanza (e), per passare da
una curva di livello a una successiva con la pendenza (p) stabilita è necessario tracciare un segmento, tra due isoipse successive, di lunghezza (d) pari
a (Fig. A.1):
e
(A.1)
d=
p
Ai fini della rappresentazione grafica, puntando il compasso in A (curva di
livello Q), con apertura pari a d (nella scala di rappresentazione della cartografia), si individuano i punti B o B 0 (curva di livello Q + e) come intersezione
dell’arco di raggio d con la curva di livello adiacente (Fig. A.1). Procedendo
allo stesso modo si passa da una curva di livello a quella successiva sino a
raggiungere il punto di destinazione fissato (Fig. A.2).
2
Appendice A
Figura A.1
Passaggio
da una curva di livello
alla successiva.
Q+e
B
d
B'
d
Q+e
tg a
p= a
d
Q
Q
A
e
d
Il processo è iterativo in quanto occorre procedere per tentativi, modificando la
pendenza dei segmenti, sino a ottenere il percorso più soddisfacente in termini
di sviluppo e configurazione planimetrica, tenendo conto anche delle eventuali
interferenze con fabbricati, corsi d’acqua ecc.
Nel caso in cui i punti B e B 0 non siano determinabili, in quanto d è minore
della distanza tra le isoipse, è possibile scegliere liberamente il punto B, senza
vincoli dettati dalla pendenza massima.
Tra gli aspetti progettuali da considerare, nell’ottica di contenere i costi e
assicurare il minore impatto ambientale e paesaggistico possibile, vi sono anche
quelli relativi all’opportunità di minimizzare i volumi di scavo e di riporto
nonché il numero e le dimensioni delle opere d’arte.
Figura A.2
Tracciolino.
142
141
B
140
139
138
13376
1
135
134
133
132
d
12
7
12
8
12
9
13
0
131
A
6
4
2
12
12
3
12
12
5
12
1
12
0
12
Se, lungo il percorso prescelto, è necessario superare un modesto corso d’acqua,
il tracciolino, adottando un criterio semplificato, deve essere mantenuto a una
quota superiore di almeno 3-5 m rispetto al pelo libero di magra. Per corsi
d’acqua importanti, la quota minima del tracciato potrà essere individuata solo
Esempio di progetto geometrico
3
dopo aver determinato, mediante specifici studi idrologici e idraulici, il livello
di piena corrispondente a un determinato periodo di ritorno (100-500 anni).
Nel caso in cui l’interferenza sia costituita da una strada o da una linea
ferroviaria esistenti, il tracciolino, qualora non sia possibile l’intersezione a
raso, deve essere mantenuto a una quota superiore di almeno 8-10 m rispetto
a tali elementi.
Le normative (CdS e Norme ferroviarie) specificano, caso per caso, le luci
minime necessarie per il superamento degli elementi descritti.
Il tracciolino, visto il numero elevato di tratti rettilinei e curve non conformi
alla normativa, deve essere rettificato con una poligonale formata da tratti
rettilinei più lunghi, raccordati da curve opportunamente dimensionate.
Step 2. Definizione della poligonale d’asse con l’inserimento di elementi geometrici a norma
Successivamente all’individuazione del tracciolino si procede con la definizione
della cosiddetta poligonale d’asse, altrimenti detta rettifica. Gli elementi di
base da impiegare sono archi di circonferenza (curve), rettifili (segmenti) e,
secondo la normativa vigente, i raccordi a raggio variabile.
Questi elementi vengono combinati, nel rispetto dei requisiti normativi,
sovrapponendosi per quanto possibile al tracciolino al fine di minimizzare i
movimenti di materia.
V
g
angolo di
deflessione
Figura A.3
Tracciamento
di una curva circolare.
"t"
saetta "s"
svilup
po
"S
"
corda "c"
T2
"t"
N
"R
gio
g /2
"
lo
g
rag
tifi
"
R"
ret
ret
tif
ilo
nte
g /2 g /4
T1
ge
M
tan
a /2
bisettrice "b"
a
O
Il tracciamento in planimetria di una curva circolare consta dei passi seguenti
(Fig. A.3):
• si misura col goniometro l’angolo al vertice ↵ (con la maggiore precisione
possibile);
• si assegna un valore a R tale per cui R > Rmin ;
• si calcola la tangente t con la seguente espressione:
↵
(A.2)
t = R · cotan
2
• si individua il centro O come punto di intersezione delle perpendicolari ai
rettifili condotte rispettivamente da T1 e T2 , distanti dal vertice V della
tangente t;
4
Appendice A
• si punta il compasso in O con apertura corrispondente a R e si traccia l’arco
di circonferenza T1 M T2 ;
• lo sviluppo S della curva circolare si determina infine mediante la seguente
relazione:
(A.3)
S = γ rad · R
dove con γ si intende l’angolo di deflessione, uguale all’angolo al centro
della curva, espresso in radianti.
Una curva circolare, per essere correttamente percepita, deve avere uno sviluppo corrispondente a un tempo di percorrenza, valutato con la velocità di
progetto della curva, di almeno 2,5 secondi (D.M. 5/11/2001).
I rapporti tra i raggi R1 e R2 di due curve circolari che, con l’inserimento
di un elemento a curvatura variabile, si succedono lungo il tracciato di strade
extraurbane di tipo A, B, C, D e F, sono regolati dall’abaco riportato nella
Figura A.4. In particolare, per le strade di tipo A e B detto rapporto deve
collocarsi nella “zona buona”; per le strade degli altri tipi è utilizzabile anche
la “zona accettabile”.
80 100
200
300 400
600 800 1000
1500
1000
ZONA DA EVITARE
1500
1500
1000
800
TT
AB
IL
E
800
CE
600
500
AC
N
300
600
500
A
O
NA
400
ZO
R 2 [m]
Figura A.4
Rapporto tra i raggi R1
ed R2 di due curve
circolari consecutive.
N
A
BU
LE
I
AB
TT
ZO
E
NA
C
AC
ZO
200
400
300
200
ZONA DA EVITARE
100
100
80
80 100
200
300 400
R 1 [m]
600 800 1000
80
1500
Tra un rettifilo di lunghezza Lr e il raggio più piccolo fra quelli delle due curve
collegate al rettifilo stesso, anche con l’interposizione di una curva a raggio
variabile, deve essere rispettata la relazione:
R > Lr
R > 400
per Lr < 300 m
per Lr > 300 m
Per evitare il superamento delle velocità consentite, la monotonia, la difficile
valutazione delle distanze e per ridurre l’abbagliamento nella guida notturna è
5
Esempio di progetto geometrico
opportuno che i rettifili abbiano una lunghezza Lr contenuta entro il seguente
limite:
(A.4)
Lr = 22 · Vp,max [m]
dove Vp,max è il limite superiore dell’intervallo di velocità di progetto della
strada, in km/h. Un rettifilo, per poter esser percepito come tale dall’utente,
deve avere una lunghezza non inferiore ai valori riportati nella Tabella A.1;
per velocità si intende la massima desunta dal diagramma di velocità per il
rettifilo considerato.
Tabella A.1
Lunghezza minima di
un rettifilo in funzione
della velocità.
Velocità [km/h]
40 50 60 70 80 90 100 110 120 130 140
Lunghezza minima [m] 30 40 50 65 90 115 150 190 250 300 360
Curve circolari di raggio costante e rettifili devono essere raccordati mediante
curve di transizione il cui raggio varia da valori elevati in prossimità del rettifilo
fino a un valore costante nella parte centrale della curva. Il D.M. del 5/11/01
ammette l’uso di un solo tipo di curva a raggio variabile detta clotoide. Essa
è progettata in modo da garantire:
• una variazione di accelerazione centrifuga non compensata (contraccolpo)
contenuta entro valori accettabili;
• una limitazione della pendenza (o sovrapendenza) longitudinale delle linee
di estremità della piattaforma;
• una corretta percezione ottica del tracciato.
La clotoide appartiene alla famiglia delle spirali generalizzate e ha la seguente
equazione (Fig. A.5):
r · s = A2
(A.5)
Figura A.5
Schema generico
inserimento clotoide.
Posizione finale
del cerchio
D
Posizione iniziale
del cerchio
M'
M
O P = Posizione clotoide iniziale
O'P' = Posizione clotoide finale
N
R
Y
R
R · cos tf
tf
D
g + a = 180°
P'
D
P
D
O'
E
tf
Yf
DR 90 – a /2
a /2
α/2
g
a
V
O
X
XM
XF
6
Appendice A
dove:
• r: raggio di curvatura nel punto P generico [m];
• s: ascissa curvilinea nel punto P generico [m];
• A: parametro di scala.
Dopo aver determinato il raggio di curva circolare più appropriato si procede
alla scelta del parametro A da utilizzare nel tracciamento della curva seguendo
i criteri stabiliti dalla normativa:
Criterio 1. Limitazione del contraccolpo
Affinché lungo un arco di clotoide si abbia una graduale variazione dell’accelerazione trasversale non compensata nel tempo, fra il parametro A e la massima
velocità V [km/h], desunta dal diagramma delle velocità, deve essere verificata
la relazione:
r
V 3 g · V · R · (qf − qi )
−
(A.6)
A > Amin =
c
c
dove:
•
•
•
•
•
•
qi : ici /100 con ici pendenza trasversale nel punto iniziale della clotoide;
qf : icf /100 con icf pendenza trasversale nel punto finale della clotoide;
R: raggio dell’arco di cerchio da raccordare [m];
V : velocità massima [km/h];
g: accelerazione di gravità [m/s2 ];
c: contraccolpo [m/s3 ].
Trascurando il secondo termine dell’espressione del radicando e assumendo per
il contraccolpo il valore limite:
cmax =
si ottiene:
50,4
V
[m/s3 ],
2
.
Amin,1 > 0.021 · Vp,max
(A.7)
Criterio 2. Sovrapendenza longitudinale delle linee di estremità della carreggiata
Nelle sezioni di estremità di un arco di clotoide la carreggiata stradale presenta
di↵erenti assetti trasversali, che vanno raccordati longitudinalmente introducendo una sovrapendenza nelle linee di estremità della carreggiata rispetto alla
pendenza dell’asse di rotazione. Nel caso in cui il raggio iniziale sia di valore
infinito, il parametro A deve verificare la seguente disuguaglianza:
s
R
· 100 · Bi · (qi + qf )
(A.8)
A > Amin,2 =
∆imax
dove:
•
•
•
•
qi : ici /100 con ici pendenza trasversale iniziale in valore assoluto;
qf : icf /100 con icf pendenza trasversale finale in valore assoluto;
R: raggio dell’arco di cerchio da raccordare [m];
Bi : distanza fra l’asse di rotazione e il ciglio della carreggiata nella sezione
iniziale della curva a raggio variabile [m];
Esempio di progetto geometrico
7
• ∆imax : sovrapendenza longitudinale massima della linea costituita dai punti
che distano Bi dall’asse di rotazione (in assenza di allargamento tale linea
coincide con l’estremità della carreggiata) che si può considerare pari a:
∆imax = 18 ·
Bi
.
V
(A.9)
Nel caso in cui anche il raggio iniziale sia di valore finito, il parametro deve
verificare la seguente disuguaglianza:
v
u
Bi · (qf − qi )
u
◆
(A.10)
A > Amin,2 = u ✓
t 1
1
∆imax
−
·
Ri Rf
100
dove:
• qi : ici /100 con ici pendenza trasversale iniziale in valore assoluto;
• qf : icf /100 con icf pendenza trasversale finale in valore assoluto;
• ∆imax : sovra pendenza longitudinale massima della linea costituita dai punti che distano Bi dall’asse di rotazione (in assenza di allargamento tale linea
coincide con l’estremità della carreggiata);
• Ri : raggio nel punto iniziale della curva a raggio variabile [m];
• Rf : raggio nel punto terminale della curva a raggio variabile [m].
Criterio 3. Corretta percezione ottica del tracciato
Per garantire la percezione ottica del tracciato deve essere verificata la seguente
relazione:
R
(A.11)
A> .
3
Inoltre, per garantire la percezione dell’arco di cerchio alla fine della clotoide,
deve risultare:
(A.12)
A 6 R.
ce
rc
hi
o
Si stabilisce il valore di A in modo che A > Amin = max (Amin,1 , Amin,2 )
verificando che R3 6 A 6 R (Fig. A.6).
di
Figura A.6
Campo di ammissibilità
parametro A.
Amin = f (Vp,c)
ne
io
er
ce
z
ap
pe
rl
ite
lim
R
=
A
Rmin = f (Vp,qmax )
ot
tic
ad
el
l'
ar
co
A
R/3 < A < R
/3
A=R
ion
ercez
r la p
pe
limite
ordo
l racc
ca de
e otti
R
L’inserimento di una clotoide tra un rettifilo e una curva circolare viene generalmente eseguito seguendo il criterio a raggio conservato, secondo cui rimane
8
Appendice A
costante il raggio R0 della curva circolare e la posizione del centro trasla lungo
la bisettrice.
Nel tracciare la poligonale d’asse è opportuno rispettare i seguenti criteri
di carattere generale (Fig. A.7):
• non discostarsi eccessivamente dal tracciolino, al fine di limitare i movimenti
di materie: riporti e sterri;
• gli angoli sottesi da lati consecutivi della poligonale d’asse devono permettere l’iscrizione di curve con raggio maggiore di quello minimo;
• qualora sia necessaria la presenza di tornanti è bene che vengano realizzati
dove la pendenza trasversale risulta minore;
• eventuali intersezioni con altre strade dovranno essere progettate in modo
da risultare ortogonali o poco discoste da tale configurazione;
• in corrispondenza di corsi d’acqua è bene che la strada sia in rettifilo e
perpendicolare al corso d’acqua in modo da ridurre le dimensioni dell’opera
d’arte.
Figura A.7
Rettifica.
142
141
140
139
B
138
13376
1
135
134
133
132
90
131
g
R
γ
13
0
a
12
7
12
8
12
9
90
A
6
2
12
12
3
12
4
12
5
12
1
12
0
12
Completata la poligonale, che costituisce la rettifica del tracciolino, è necessario inserire i “picchetti” ubicandoli secondo vari criteri di massima, integrabili
tra di loro (Fig. A.8):
• in corrispondenza dei punti notevoli (tangenti, bisettrici ecc.) delle curve e
delle clotoidi;
• in corrispondenza delle intersezioni dell’asse con le isoipse;
9
Esempio di progetto geometrico
• secondo interassi stabiliti e convenienti per la definizione del tracciato (per
esempio ogni 30 m) e a seconda dello sviluppo degli elementi costituenti il
tracciato;
• in corrispondenza delle strutture di approccio delle eventuali opere d’arte
(ponti, viadotti, muri di sostegno ecc.)
Una volta definito l’asse longitudinale medio del tracciato, si deve considerare
la larghezza di ingombro e↵ettiva della piattaforma, che dipende direttamente
dalla tipologia di strada scelta (Fig. A.9).
Per curve circolari aventi raggi ridotti, ancorché superiori a Rmin , occorre verificare la necessità di prevedere allargamenti in curva, per consentire la
sicura iscrizione dei veicoli, soprattutto pesanti, garantendo i necessari franchi tra la sagoma limite dei veicoli e i margini di corsia. Il calcolo secondo
normativa si esegue applicando la relazione:
E=
K
R
(m)
(A.13)
142
141
140
139
Figura A.8
Inserimento
dei picchetti.
17
B
16
138
13376
1
15
14
13
135
134
133
132
12 t
11
131
10
13
0
9b
12
9
8
12
8
7
6t
12
7
5
4
6
12
A
3
2
12
2
12
3
12
4
12
5
1
1
12
0
12
dove:
• K: costante a valore 45;
• R: raggio esterno della corsia in metri.
L’allargamento E cosı̀ ottenuto va applicato solo se il valore è superiore a
0,20 m.
Appendice A
Figura A.9
Ingombro
della piattaforma
stradale.
142
141
17
140
139
138
137
136
B
16
15
14
13
135
134
133
132
12 t
11
131
10
13
0
9b
12
9
8
12
8
7
6t
12
7
5
4
6
12
A
3
2
12
2
3
12
4
12
5
1
12
10
1
12
0
12
Andamento altimetrico
Terminato il progetto planimetrico, è necessario esaminare il tracciato, dal
punto di vista altimetrico, mediante il profilo longitudinale che rappresenta
graficamente l’andamento altimetrico del terreno in corrispondenza dell’asse
del tracciato.
Per disegnare il profilo longitudinale si assume una quota (intera) di riferimento inferiore alla quota di progetto minima; sul segmento che, nel disegno,
rappresenta tale quota vengono riportate le distanze parziali e progressive dei
picchetti.
In corrispondenza di ogni picchetto si traccia, a partire dalla quota di riferimento, un segmento verticale di lunghezza pari al dislivello, in quel punto,
fra la quota di riferimento e quella del terreno.
Unendo le estremità superiori di tutti i segmenti, si ottiene una spezzata,
che rappresenta il profilo longitudinale del terreno lungo l’asse della strada (la
cosiddetta linea nera). Per rendere il profilo longitudinale chiaro e leggibile le
quote vengono generalmente rappresentate in una scala 10 volte maggiore di
quella caratterizzante le distanze.
L’andamento del profilo del terreno, cosı̀ ottenuto, è irregolare per cui, per
poter definire l’andamento altimetrico dell’asse stradale, è necessario regolarizzarlo sostituendo alla linea nera una poligonale d’asse formata da livellette
a pendenza costante raccordate da archi di parabola quadratica.
22.752
26.623
17.522
0
-2,50%
ANDAMENTO CIGLI
PENDENZE TRASVERSALISinistro -2,50%
Destro
ANDAMENTO PLANIMETRICO
ETTOMETRICHE
L=112.00
-2,50%
-2,50%
1
6
5
4
9.667
7
-7,00%
7.00%
QUOTE PROGETTO
19.824
3
1500.000
32.443
32.490
0.351
64.880
4.32536%
QUOTE TERRENO
25.276
2
R
T1
T2
BS
SV
DP
50.001
122.731
2
122.131
122.131
DISTANZE PARZIALI
1
Lunghezze 1: 1000
DISTANZE PROGRESSIVE
No. SEZIONI
Q.RIF. 120.00
Altezze 1: 100
0.00
125,00
130,00
135,00
IR 17.560 (122,342)
-0,55
123.000
122.454
0.001
-1,07
124.000
122.925
25.277
-1,21
125.000
123.788
45.101
-0,81
67.853
PROG
Q
FR 82,441 (124,523)
94.476
0.001
122.131
23.535
8
12.939
9
11.369
20.385
11
10
R=50.00
L=92.28
2
14.387
12
7.855
30.615
-7,00%
7.00%
-2,50%
-2,50%
L=112.68
3
17
16
Z
-2,50%
-2,50%
316.960
135.000
4
15
25.140
PROG
Q
14
24.563
2000.000
46.060
45.992
0.529
91.980
-4.59902%
263.000
134.500
3
13
24.507
R
T1
T2
BS
SV
DP
PROG
Q
128.000
127.991
1
128.550
128.706
PROG
Q
128.996
129.334
-0,47
126.000
D=0,500 L=53,960
P=0,926%
130.000
130.461
-0,31
125.188
D=11,769 L=212,999
P=5,525%
130.682
131.256
D=0,600 L=50,000
P=1,200%
131.002
131.690
111.998
126.631
126.157
-0,01
132.000
132.947
145.200
0,16
133.000
133.913
158.139
0,34
169.508
0,6
189.894
134.000
134.588
121.665
127.000
126.691
212.135
0,95
236.642
0,91
261.205
0,59
286.345
0,57
0,69
IR 217,010 (131,959)
204.281
FR308.990 (134.926)
0,00
316.960
135.000
135.000
LIVELLETTE
Esempio di progetto geometrico
11
Figura A.10
Profilo longitudinale.
12
Appendice A
Nella definizione del profilo di progetto (linea grigio scuro) è opportuno cercare
di compensare le aree di sterro e quelle di riporto in prospettiva del possibile
riutilizzo del terreno (tenendo conto delle restrizioni definite dalla normativa
sul riutilizzo delle terre e rocce da scavo, D.M. 10/08/2012, n. 161) (Fig. A.10).
Al di sotto della quota di riferimento, nella fincatura di base, vengono
riportati, secondo un ordine che può variare (Fig. A.11):
•
•
•
•
•
•
•
•
•
il numero dei picchetti in ordine progressivo;
le distanze progressive a partire dall’origine;
le distanze parziali fra un picchetto e il successivo;
la quota del terreno in corrispondenza di ogni picchetto d’asse;
la quota di progetto in corrispondenza di ogni picchetto d’asse;
le distanze ettometriche;
i rettifili e le curve;
l’andamento delle pendenza trasversali della piattaforma;
la lunghezza e la pendenza delle livellette.
Figura A.11
Fincature del profilo.
D=0,600 L=50,000
P=1,200%
LIVELLETTE
2
1
PROG 50,001
Q
122.731
PROG 0,001
Q
122.131
DISTANZE PARZIALI
19.824
122.454 123.000
QUOTE PROGETTO
122.131 122.131
QUOTE TERRENO
25.276
45.101
DISTANZE PROGRESSIVE
3
2
122.925 124.000
1
25.277
No. SEZIONI
0,001
R 1500.000
T1
32.443
T2
32.490
BS
0.351
SV 64.880
DP 4.32536%
0
ETTOMETRICHE
ANDAMENTO PLANIMETRICO
Destro
ANDAMENTO CIGLI
PENDENZA TRASVERSALI Sinistro
-2,50%
-2,50%
Come accennato in precedenza due livellette consecutive che presentano bruschi cambiamenti di pendenza devono essere raccordate secondo normativa da
un arco di parabola quadratica. I raccordi verticali possono essere di due tipi:
convessi (dossi) o concavi (sacche) (Fig. A.12).
Esempio di progetto geometrico
13
DOSSO
Figura A.12
Raccordi verticali.
visibilità
h1
h2
p
p1
2
T1
T2
SACCA
visibilit
à
p
1
h
D
p2
q
T1
T2
Il tracciamento del generico raccordo altimetrico avviene secondo i passi
seguenti:
• Si determina la lunghezza orizzontale l del raccordo (Fig. A.13):
l = K · |p2 − p1 |
dove:
(A.14)
• p1 = pendenza prima livelletta [valore decimale];
• p2 = pendenza seconda livelletta [valore decimale];
Velocità [km/h]
48
64
80
96
112
K Raccordi concavi 1000 1500 2500 3500 4500
Raccordi convessi 800 1500 2800 5000 8000
O = T1
Figura A.13
Inserimento raccordi
verticali.
T2
YT 2
2
p
A
X
M
p
1
l/2
V
l/2
Per raccordi convessi (dossi):
• se la distanza di visibilità da realizzare è inferiore allo sviluppo l:
Rv =
D2
p
2 · (h1 + h2 + 2 · h1 · h2 )
Tabella A.2
Valori di K per raccordi
concavi e convessi.
B
l
Y
asse parabola
• K = coefficiente dipendente dalla velocità di progetto
(Tab. A.2).
• in riferimento alla Figura
A.13 si individuano graficamente i punti di tangenza
T 1 e T2 ;
• si determina il raggio Rv del
cerchio osculatore tangente
alla parabola nel vertice M
con gli abachi o le formule
fornite dal D.M. 5/11/01.
[m];
(A.15)
14
Appendice A
• se la distanza di visibilità da realizzare è maggiore allo sviluppo l:
"
#
p
2 · 100
h1 + h2 + 2 · h1 · h2
Rv =
· D − 100 ·
[m]
(A.16)
∆i
∆i
dove:
– D: distanza di visibilità da realizzare [m];
– ∆i: variazione di pendenza tra le due livellette [%];
– h1 : altezza sul piano stradale dell’occhio del conducente [m], di norma
si pone pari a 1,1 m;
– h2 : altezza dell’ostacolo [m], in caso di visibilità per l’arresto è pari a
0,10 m, in caso di visibilità per il sorpasso è pari a 1,10 m.
Rv può essere determinato anche mediante l’utilizzo di abachi: la Figura A.14
fornisce, per diversi valori di D, le lunghezze di Rv quando h1 = 1,10 m e
h2 = 0,10 m. La Figura A.15 si riferisce invece al caso in cui h1 = h2 = 1,10 m.
Figura A.14
Abaco
per la determinazione
di Rv per h1 = 1,10 m e
h2 = 0,10 m.
35000
D>L
D<L
D = 340 m
30000
D = 320 m
Raggio Verticale R v [m]
25000
D = 300 m
D = 280 m
20000
D = 260 m
D = 240 m
15000
D = 220 m
D = 200 m
10000
D = 175 m
D = 150 m
5000
0
0,6
0,8 1
2
3
4
5
D = 125 m
D = 100 m
D = 75 m
D = 50 m
6 7 8 9 10
Variazione di pendenza ∆i[%]
Per i raccordi concavi (sacche):
• se la distanza di visibilità da realizzare è inferiore allo sviluppo l:
Rv =
D2
2 · (h + D · sen #)
[m]
(A.17)
Esempio di progetto geometrico
15
• se la distanza di visibilità da realizzare è maggiore allo sviluppo l:
�

2 · 100
100
Rv =
· (h + D · sen #)
D−
[m]
(A.18)
∆i
∆i
40000
D>L
35000
D<L
D = 550 m
30000
Raggio Verticale R v [m]
D = 500 m
25000
D = 450 m
20000
D = 400 m
15000
D = 350 m
D = 300 m
D = 275 m
D = 250 m
D = 225 m
D = 200 m
D = 175 m
D = 150 m
10000
5000
0
0.6
0.8
1
2
3
4
5
6 7 8 910
Variazione di pendenza ∆ i[%]
dove:
– D: distanza di visibilità da realizzare [m];
– ∆i: variazione di pendenza tra le due livellette [%];
– h: altezza del centro dei fari del veicolo sul piano stradale [m];
– ✓: massima divergenza verso l’alto del fascio luminoso rispetto all’asse
del veicolo.
Ponendo h = 0,5 m e ✓ = 1◦ si hanno i valori di Rv riportati in Figura A.16.
Si verificano le limitazioni imposte dalla normativa al raggio Rv , deve
risultare:
• Rv > 40 m per raccordi concavi;
• Rv > 20 m per raccordi convessi;
• av = (vp )2 /Rv 6 0,6 m/s2 , dove vp è la velocità di progetto della curva
[m/s].
Figura A.15
Abaco
per la determinazione
di Rv per
h1 = h2 = 1,10 m.
16
Appendice A
Si calcolano le coordinate XM e YM avvalendosi delle seguenti formule:
i1 (%)
100
[m]
(A.19)
1
i (%)
2
· (XM ) +
⌥ XM
2 · Rv
100
[m].
(A.20)
XM = Rv ·
YM = −
10000
Figura A.16
Abaco
per la determinazione
di Rv per h = 0,5 m e
✓ = 1◦ .
D>L
9000
D<L
D = 340 m
D = 320 m
8000
D = 300 m
D = 280 m
7000
Raggio Verticale R v [m]
D = 260 m
D = 240 m
6000
D = 220 m
D = 200 m
5000
D = 175 m
4000
D = 150 m
3000
D = 125 m
D = 100 m
2000
D = 75 m
1000
D = 50 m
0
1
2
3
4
5
6
7 8 9 10
Variazione di pendenza ∆ i[%]
La costruzione del raccordo altimetrico avviene per punti tenendo conto delle
diverse scale di riduzione rispettivamente delle distanze e delle altezze.
Sezioni tipo e sezioni stradali
Dopo aver progettato l’andamento plano-altimetrico del tracciato devono essere definite le sezioni stradali. Esse evidenziano l’andamento trasversale del
corpo stradale e del terreno rappresentandone le intersezioni, in corrispondenza dei picchetti, con un piano verticale normale all’asse stradale. Occorre però
prima definire nel particolare le caratteristiche costruttive della piattaforma,
la pendenza delle scarpate laterali, la tipologia di sistemazione degli elementi
marginali, i particolari degli elementi accessori. Tali informazioni di dettaglio
sono descritte dalle sezioni tipo, mentre le sezioni stradali riportano solo le
informazioni generali descrittive del solido stradale. Dal punto di vista delle
quote del terreno e di progetto, le tipologie possibili di sezione, nel caso in
esame, sono tre: rilevato, trincea e mezzacosta.
17
Esempio di progetto geometrico
Nelle sezioni in rilevato la linea del terreno si trova a un livello inferiore rispetto
a quella di progetto (Fig. A.17).
CIGLIO
(arginello)
PIATTAFORMA
BANCHINA
CORSIA
CORSIA
Q.P.
2,50%
Figura A.17
Sezione tipo in rilevato.
CIGLIO
(arginello)
BANCHINA
2,50%
3
FOSSO DI VAR.
GUARDIA
2
VAR. FOSSO DI
GUARDIA
1
1
Nelle sezioni realizzate in trincea accade il contrario: la linea del terreno si
trova infatti a una quota più elevata rispetto a quella di progetto (Fig. A.18).
Figura A.18
Sezione tipo in trincea.
FOSSO DI
GUARDIA
CIGLIO
(cunetta)
VAR.
BANCHINA
CORSIA
PIATTAFORMA
CORSIA
CIGLIO
(cunetta)
BACHINA
VAR.
1
2,50%
Q.P.
1
2
3
FOSSO DI
GUARDIA
1
1
2,50%
Le sezioni a mezzacosta sono caratterizzate da una parte in trincea e da una
in rilevato (Fig. A.19).
FOSSO DI
GUARDIA
CIGLIO
(cunetta)
BACHINA
VAR.
3
PIATTAFORMA
CORSIA
CORSIA
CIGLIO
(arginello)
Figura A.19
Sezione tipo
a mezzacosta con
gradonatura.
BACHINA
1
2 1
2,50%
Q.P.
2,50%
3
2
VAR. FOSSO DI
GUARDIA
1
1
18
Appendice A
Le sezioni vengono generalmente rappresentate come appaiono a un osservatore che percorre, dall’inizio alla fine, l’intero tracciato, volgendo le spalle
all’origine della strada.
Per ricavare le sezioni si procede nel modo seguente:
1. si riportano le quote di progetto e del terreno in corrispondenza dell’asse
stradale su di un sistema cartesiano, assegnando una quota di riferimento
opportuna all’asse delle ascisse (Fig. A.20).
QUOTE TERRENO
15
134
QUOTE PROGETTO
316.960
286.345
30.615
ASSE
STRADALE
133
25.140
135.000
DISTANZE PARZIALI
135.000
16
17
134.000
DISTANZE PROGRESSIVE
16
15
134.588
B
133.000
137
136
135
No. SEZIONI
17
261.205
139
138
133.913
Figura A.20
Identificazione
delle quote della linea
di progetto
e del terreno.
QUOTA DI
RIFERIMENTO
2. si riporta la traccia del piano di sezione, misurando a destra e a sinistra le
quote e le distanze del terreno esistente rispetto all’asse (Fig. A.21).
D
133
135.000
134
QUOTE TERRENO
QUOTE PROGETTO
135.000
lD
lS
134.000
QUOTA DI
RIFERIMENTO
30.615
134.000
15
25.140
134.588
135
DISTANZE PARZIALI
S
136
133.000
16
DISTANZE PROGRESSIVE
17
133.913
137
16
15
316.960
B
286.345
No. SEZIONI
17
138
261.205
139
ASSE
STRADALE
Figura A.21
Piano di sezione.
134.588
Esempio di progetto geometrico
19
3. si riporta l’andamento trasversale del terreno (Fig. A.22).
LS
LD
ASSE
STRADALE
Figura A.22
Sezione trasversale
del terreno.
135.000
S
134.000
134.588
133.000
D
QUOTA DI
RIFERIMENTO
ASSE
STRADALE
4. si riporta la sezione della piattaforma stradale relativa alla tipologia di
strada scelta, applicando le pendenze trasversali della piattaforma calcolate
in precedenza (Fig. A.23).
S
134.588
Figura A.23
Sezione trasversale
della piattaforma.
p%
banchina+corsiacorsia+banchina
Cunetta
PIATTAFORMA
D
Arginello
QUOTA DI
RIFERIMENTO
5. si completa la sezione con l’andamento delle scarpate, applicando alle scarpate in rilevato la pendenza 2/3 (66.67%), mentre la pendenza delle scarpate in trincea, a seconda delle caratteristiche del terreno in posto, può
variare da 1/1 (100%) a 2/3, oppure anche a pendenze inferiori in terreni
particolarmente sfavorevoli (Fig. A.24).
6. una volta disegnata la sezione, a seconda del livello di definizione del progetto (preliminare, definitivo, esecutivo) si potrà completare l’elaborato
aggiungendo ulteriori informazioni descrittive, quali per esempio: gli spessori della pavimentazione, gli strati di rivestimento e di bonifica dei piani
di posa, i fossi di guardia ecc. Al termine delle operazioni di costruzione
della sezione si procede alla quotatura degli elementi principali (Fig. A.25).
20
Appendice A
ASSE
STRADALE
Figura A.24
Completamento
sezione.
STERRO
1
1
3
2
S
RILEVATO
134.588
p%
3
2
D
banchina+corsiacorsia+banchina
Cunetta
Arginello
PIATTAFORMA
ASSE
STRADALE
QUOTA DI
RIFERIMENTO
Figura A.25
Sezione trasversale
definitiva.
134.588
2.50%
3
2
14,54
133.66
1,25 1,19
134.46
134.74
5,25
134.59
QUOTE
PROGETTO
5,25
134.46
1,03 1,25
134.46
DISTANZE
PROGETTO
133.00
134.00
14.20
135.00
QUOTE
TERRENO
134.46
Q.R. 128
DISTANZE
TERRENO
Calcolo dei volumi
Una volta definite le sezioni si e↵ettua il calcolo dei volumi di sterro e riporto.
Per calcolare il volume del solido stradale compreso tra due sezioni trasversali
consecutive si approssima tale corpo con un prismoide delimitato dal piano
di campagna, dalla piattaforma, dalle scarpate del rilevato e/o della trincea e
dalle sezioni trasversali terminali del tronco considerato (Fig. A.26).
Il volume del prismoide viene calcolato utilizzando la formula di Torricelli,
nota anche con il nome di formula delle sezioni ragguagliate. In riferimento
alla Figura A.26 si ha:
V =
A1 + A2
·D
2
[m3 ].
(A.21)
Esempio di progetto geometrico
A1
21
Figura A.26
Prismoide tra due
sezioni in rilevato.
D
A2
A seconda della tipologia di sezioni consecutive si possono avere quattro diversi
casi:
1) Solido stradale tra due sezioni omogenee di riporto o sterro (Fig. A.27).
Il volume si calcola, analogamente a quanto visto in precedenza, come:
V =
R 1 + R2
·D
2
[m3 ]
(A.22)
dove:
• R1 : area della prima sezione [m2 ];
• R2 : area della seconda sezione [m2 ];
• D: distanza tra le due sezioni [m].
1
R1
Figura A.27
Sezioni omogenee.
R1
D
R2
D
2
R2
2) Solido stradale tra due sezioni eterogenee, una in trincea e una in rilevato
(Fig. A.28).
22
Appendice A
Figura A.28
Sezioni eterogenee.
S
S
dS
dS
D
Linea di passaggio teorica
D
dR
dR
R
R
In questo caso vengono calcolati separatamente il volume di sterro e quello di
riporto, mediante le seguenti formule:
S
· dS [m3 ]
2
D
con dS =
· S [m]
S+R
R
VR = · dR [m3 ]
2
D
con dR =
· R [m]
S+R
VS =
(A.23)
(A.24)
(A.25)
(A.26)
dove:
•
•
•
•
•
•
•
dS : distanza della linea di passaggio dalla sezione di sterro [m];
dR : distanza della linea di passaggio dalla sezione di riporto [m];
VS : volume del cuneo di sterro [m3 ];
VR : volume del cuneo di riporto [m3 ];
R: area di riporto [m2 ];
S: area di sterro [m2 ];
D: distanza tra le due sezioni [m].
3) Solido stradale tra una sezione in rilevato o trincea e una sezione mista
(Fig. A.29).
In questo caso per determinare il volume bisogna scomporre il corpo stradale mediante un piano verticale passante per il punto M 0 e diretto secondo
l’asse della strada. Il corpo stradale viene quindi diviso in due parti: a sinistra
della linea M 0 M si ha un prismoide, mentre a destra due cunei. Il volume del
prismoide di riporto viene calcolato come:
VR0 =
R10 + R2
·D
2
[m3 ]
(A.27)
Esempio di progetto geometrico
M
1
R'1
Figura A.29
Sezione mista
e sezione in rilevato.
R"1
dR
Linea di passaggio
D
dS
S2
2
R2
M'
dove:
• R10 : area in rilevato a sinistra della linea di passaggio M 0 M nella prima
sezione [m2 ];
• R2 : area in rilevato della seconda sezione [m2 ];
• D: distanza tra le due sezioni [m].
Il volume dei cunei di sterro e riporto situati a destra della linea M 0 M vengono
calcolati mediante le seguenti espressioni:
R100
· dR
2
D
con dR =
S2 + R100
S2
VS00 =
· dS
2
D
con dS =
S2 + R100
VR00 =
[m3 ]
· R100
(A.28)
[m]
[m3 ]
· S2
(A.29)
(A.30)
[m]
(A.31)
dove:
•
•
•
•
•
R100 : area in rilevato a destra della linea M 0 M nella prima sezione [m2 ];
dR : distanza della linea di passaggio dalla sezione di riporto [m];
S2 : area in trincea a destra della linea M’M nella seconda sezione [m2 ];
dS : distanza della linea di passaggio dalla sezione di sterro [m];
D: distanza tra le due sezioni [m].
Sommando i contributi dati dai volumi calcolati a destra e a sinistra della linea
di passaggio si ottiene:
• volume sterro: VS = VS00 ;
• volume riporto: VR = VR0 + VR00 .
23
24
Appendice A
4) Solido stradale tra due sezioni miste con punti di passaggio sfalsati (Fig. A.30).
Figura A.30
Sezioni miste.
S1
R"1
1
R'1
Linea di
passaggio
D
S'2
R2
S"2
2
P2
Per determinare il volume, il solido viene diviso in tre parti con due piani
verticali paralleli all’asse della strada e passanti rispettivamente per i punti
P1 e P2 . Il corpo stradale viene quindi diviso in tre parti: a sinistra della linea
passante per P2 si ha un prismoide di riporto, nella parte centrale si hanno
due cunei e a destra della linea passante per P1 si ha un prismoide di sterro.
Il volume del prismoide di riporto viene calcolato come:
VR0 =
R10 + R2
·D
2
[m3 ]
(A.32)
dove:
• R10 : area in rilevato a sinistra della linea passante per P2 nella prima sezione
[m2 ];
• R2 : area in rilevato della seconda sezione [m2 ];
• D: distanza tra le due sezioni [m].
Il volume dei cunei di sterro e riporto situati tra le linee passanti per P1 e P2
vengono calcolati mediante le seguenti espressioni:
R100
· dR
2
D
con dR = 0
S2 + R100
S0
VS00 = 2 · dS
2
D
con dS = 0
S2 + R100
VR00 =
[m3 ]
· R100
(A.33)
[m]
[m3 ]
· S20
(A.34)
(A.35)
[m]
(A.36)
Esempio di progetto geometrico
dove:
• R100 : area in rilevato compresa tra le linee passanti per P1 e P2 nella prima
sezione [m2 ];
• dR : distanza della linea di passaggio dalla sezione di riporto [m];
• S20 : area in trincea compresa tra le linee passanti per P1 e P2 nella seconda
sezione [m2 ];
• dS : distanza della linea di passaggio dalla sezione di sterro [m];
• D: distanza tra le due sezioni [m].
Il volume del prismoide di sterro viene calcolato come:
VS0 =
S200 + S1
·D
2
[m3 ]
(A.37)
dove:
• S20 : area in trincea a destra della linea passante per P1 nella seconda sezione
[m2 ];
• S1 : area in trincea a destra della linea passante per P1 nella prima sezione
[m2 ];
• D: distanza tra le due sezioni [m].
Sommando i contributi dati dai volumi calcolati per le tre parti in cui è stato
diviso il solido stradale si ottiene:
• volume sterro: VS = VS0 + VS00 ;
• volume riporto: VR = VR0 + VR00 .
Computo metrico estimativo
La fase finale del progetto stradale consiste nella redazione di un computo metrico estimativo in cui vengono riportate le indicazioni relative alle lavorazioni
e alle opere d’arte necessarie per la realizzazione della strada.
Generalmente il computo viene suddiviso in due capitoli principali: opere
da conteggiare “a corpo” e opere da conteggiare “a misura”.
Nella parte a corpo vengono computate tutte le opere o parti di opera che
risultano ben definite e per le quali, in fase costruttiva, non si prevedono variazioni geometriche sostanziali. Esempi di opere da computare a corpo possono
essere: le elevazioni e gli impalcati di ponti e viadotti, le opere fuori terra in
genere, le finiture, i movimenti di materie (quindi scavi e rilevati) a eccezione
degli strati di bonifica dei piani di posa.
Nelle parte a misura, invece, si computano quelle lavorazioni che, seppur
progettate in base a campagne dettagliate di indagini dei terreni, dell’idrologia
esistente, ecc., possono presentare rischi di imprevisto geologico o altro; in tal
caso vi può essere la possibilità di avere sottodimensionato o sovrastimato la
geometria o le caratteristiche costruttive delle opere. Esempi classici di lavorazioni da computare a misura sono: le fondazioni sia dirette sia su pali, gli
scavi in sezione per la loro esecuzione, le bonifiche e le preparazioni dei piani
di posa da eseguire al di sotto dei rilevati. Recentemente le Amministrazioni
committenti tendono sempre più spesso, anche alla luce delle normative in
materia di contratti pubblici, a imporre la realizzazione di appalti completamente a corpo, in ragione di una razionalizzazione dei costi e di una maggiore
25
26
Appendice A
responsabilizzazione di tutti gli operatori coinvolti nei processi decisionali e
realizzativi delle opere pubbliche.
La struttura del computo sia per la parte a corpo sia per quella a misura,
dovrebbe essere realizzata per sottocapitoli omogenei e per singola opera; per
esempio una struttura tipo potrebbe essere la seguente:
• movimenti di materie, dove si computano gli scavi, i rilevati, le demolizioni;
• opere d’arte maggiori, quali ponti e viadotti, suddivisi individualmente e
con i relativi sottocapitoli (elevazioni, impalcati, finiture ecc.);
• opere d’arte minori, quali muri di sostegno, tombini scatolari e circolari;
• sovrastrutture stradali, quindi le fondazioni stradali e le pavimentazioni;
• barriere di sicurezza;
• segnaletica orizzontale e verticale.
All’interno del computo metrico estimativo le voci, a seconda della tipologia
della lavorazione, possono essere computate per unità di volume, di peso, di
area o di lunghezza.
Per esempio si computano per volume:
•
•
•
•
•
•
•
gli scavi di sbancamento;
gli scavi a sezione obbligata di fondazione;
le operazioni di realizzazione dei rilevati stradali;
la fornitura dei materiali da rilevato;
la realizzazione delle fondazioni stradali;
il conglomerato cementizio per le opere d’arte;
i materiali per i drenaggi.
Le voci che si computano per peso possono essere:
• l’acciaio in barre ad aderenza migliorata per le armature delle opere d’arte;
• l’acciaio di carpenteria per gli impalcati metallici.
Possono essere computate per superficie, invece:
•
•
•
•
•
la preparazione e compattazione del piano di posa dei rilevati;
la fornitura e la posa dei teli geotessili anticontaminanti;
i conglomerati bituminosi per strati di usura, binder e base;
le casseforme per le strutture in conglomerato cementizio;
i rivestimenti delle scarpate con terreno vegetale.
Alcune voci computate per lunghezza posso essere:
•
•
•
•
la
la
la
la
fornitura
fornitura
fornitura
fornitura
e
e
e
e
posa
posa
posa
posa
in
in
in
in
opera
opera
opera
opera
di
di
di
di
pali in calcestruzzo;
tubi drenanti e di aerazione;
cunette;
barriere di sicurezza.
Il computo metrico estimativo viene realizzato sulla base di un elenco prezzi
che fornisce il costo unitario di ciascuna categoria di lavorazione necessaria
per la realizzazione dell’infrastruttura viaria. In genere ogni amministrazione
ha il proprio listino prezzi, ma come riferimento generale è consigliabile, almeno per la vastità delle varie lavorazioni previste, fare riferimento ai prezziari
più comunemente utilizzati quali gli elenchi prezzi Anas, emessi periodicamente dai vari compartimenti regionali, oppure gli analoghi documenti delle
concessionarie autostradali.
Esempio di progetto geometrico
Per ottenere il costo dell’intervento specifico il prezzo unitario deve essere
moltiplicato per il quantitativo di lavorazione. La somma di tutti i costi d’intervento determinano la stima economica dei lavori costituenti l’opera progettata. Vanno però computati anche i costi relativi alla sicurezza, e gli importi
delle somme a disposizione dell’amministrazione, quali le somme per gli espropri, per la risoluzione delle interferenze, gli oneri fiscali, e ogni altro onere
necessario al completamento dell’opera. La somma degli importi relativi ai lavori, alla sicurezza, alle somme a disposizione, rappresenta il costo complessivo
dell’opera per l’ente committente.
27