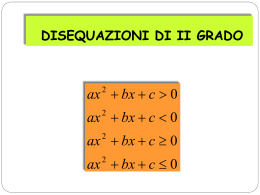
Disequazioni
di 2° grado
Metodo grafico
Anna Ippolito - Elisa Sansoni
1
Disequazione di 2° grado

Una disequazione di secondo grado in una incognita è
riconducibile ad una delle seguenti forme
ax  bx  c  0
ax  bx  c  0
ax 2  bx  c  0
ax 2  bx  c  0
2
2
Anna Ippolito - Elisa Sansoni
2
Disequazione di 2° grado

Risolvere una disequazione di 2° grado significa
determinare i valori dell’incognita x che rendono la
funzione y  ax 2  bx  c positiva oppure negativa

Graficamente significa determinare i valori di x in
corrispondenza dei quali i punti della parabola hanno
ordinata (cioè y) positiva (la parabola sta sopra l’asse
delle x) o negativa (la parabola sta sotto l’asse delle x)
Anna Ippolito - Elisa Sansoni
3
Esploriamo il problema
0
Risolvere la disequazio ne x 2  2x  3  0
 bisogna determinare i valori di x in
corrispond enza dei quali la parabola
y  x 2  2x  3 sta sopra l' asse delle x (y  0)
 ALGORITMO
si risolve l' equazione x 2  2x  3  0
x1,2  1  1  3  1  2
Δ  0  x1  1
x2  3
 i valori di x per i quali
la parabola è positiva (sta sopra l' asse x)
sono : - ;-1  3;
Anna Ippolito - Elisa Sansoni
4
Esploriamo il problema
0
Risolvere la disequazio ne x 2  8x  16  0
 bisogna determinare i valori di x in
corrispond enza dei quali la parabola
y  x 2  8x  16 sta sotto l' asse delle x (y  0)
ALGORITMO
 si risolve l' equazione x 2  8x  16  0
x1,2  4  16  16  4
Δ  0  x1  x 2  4
 non ci sono valori di x per i quali
la parabola è negativa (sta sotto l' asse x)
quindi l' insieme delle soluzioni è vuoto :
Anna Ippolito - Elisa Sansoni
S 
5
Esploriamo il problema
0
Risolvere la disequazio ne x 2  4x  10  0
 bisogna determinare i valori di x in
corrispond enza dei quali la parabola
y  x 2  4x  10 sta sopra l' asse delle x (y  0)
ALGORITMO
 si risolve l' equazione x 2  4x  10  0
x1,2  2  4  10
Δ  0   soluzioni reali
 in corrispond enza di ogni valore di x
la parabola è positiva (sta sopra l' asse x)
quindi l' insieme delle soluzioni è : S  R
Anna Ippolito - Elisa Sansoni
6
E se a è negativo????
Risolvere la disequazio ne - 4x 2  3x  1  0
Cambio i segni e il verso della disuguagli anza :
4x 2  3x  1  0  questa è la disequazio ne da risolvere
 bisogna determinare i valori di x in
corrispond enza dei quali la parabola
y  4x 2  3x  1 sta sotto l' asse delle x (y  0)
ALGORITMO
 si risolve l' equazione 4x 2  3x  1  0
3  9  16 3  5

8
8
1
Δ  0  x1  1
x2  
4
x1,2 
 i valori di x per i quali
la parabola è negativa (sta sotto l' asse x)
 1 
sono : - ;1
Anna Ippolito - Elisa Sansoni
 4 
7
ALGORITMO
1.
2.
Se a <0 si cambiano i segni e il verso
della disequazione in modo che la
parabola abbia la concavità rivolta
verso l’alto
Si risolve l’equazione associata
Anna Ippolito - Elisa Sansoni
8
ALGORITMO Δ>0
l’equazione ha due soluzioni reali x1 e x2
La parabola sta un po’ sopra e un po’ sotto l’asse x

ax2+bx+c>0 per valori esterni all’intervallo delle soluzioni:
x  x1  x  x2

ax2+bx+c≥0 per valori esterni all’intervallo delle soluzioni:
x  x1  x  x2

S   ; x1   x2 ;
ax2+bx+c<0 per valori interni all’intervallo delle soluzioni:
x1  x  x2

S   ; x1   x2 ;
S  x1 ; x2 
ax2+bx+c≤0 per valori interni all’intervallo delle soluzioni:
x1  x  x2
Anna Ippolito - Elisa Sansoni
S  x1 ; x2 
9
ALGORITMO Δ=0
l’equazione ha due soluzioni coincidenti x1≡x2
La parabola sta sempre sopra l’asse x ed è tangente ad esso nel punto x1≡ x2

ax2+bx+c>0
per ogni valore di x | x≠x1:
x  x1, 2

ax2+bx+c≥0 per ogni valore di x:
x  R

SR
ax2+bx+c<0 per nessun valore di x:
x  R

S  R \ x1 
ax2+bx+c≤0 per x=x1:
x  x1
Anna Ippolito - Elisa Sansoni
S 
Sx1 
10
ALGORITMO : Δ<0
l’equazione non ha soluzioni reali
La parabola sta sempre sopra l’asse x

ax2+bx+c>0 o ax2+bx+c≥0
x  R

SR
ax2+bx+c<0 o ax2+bx+c≤0
x  R
per ogni valore di x:
per nessun valore di x:
S 
Anna Ippolito - Elisa Sansoni
11