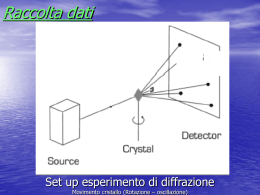
Diffrazione di raggi X su polveri
Cenni di cristallochimica
•Generazione dei raggi X
•Diffrazione dei raggi X da parte dei cristalli
•Equazioni di Laue e Legge di Bragg
•Metodi diffrattometrici
•Motodo delle Polveri (Solidi policristallini)
•Applicazioni e descrizione esercitazioni
Testi Consigliati:
ƒA. R. West, Solid State Chemistry and its Application, John Wiley & Sons
Il cristallo è un corpo anisotropo omogeneo costituito da un ordine
periodico tridimensionale di atomi o ioni o molecole
La distribuzione di ioni atomi o molecole è periodicamente
omogenea in tre dimensioni
I solidi possono presentarsi in forma di:
ƒmonocristalli (periodicità perfetta su tutto il solido),
ƒpolicristalli (grani di dimensione variabile separati da bordi di grano
I solidi possono anche essere
ƒAmorfi o non-cristallini
Reticolo cristallino
La disposizione periodica tridimensionale tipica dei cristalli può essere
rappresentata attraverso un reticolo (ovvero una griglia di punti).
A ciascun punto del reticolo può corrispondere un atomo, una molecola, una
serie di molecole etc. a seconda della complessità del sistema.
c b
a
Nel caso del Polonio a ciascun punto corrisponde un atomo
Cella Unitaria (la più piccola unità di ripetizione che
mostra la simmetria completa della struttura cristallina)
c b
a
Prendiamo un sistema di assi cristallografici a, b, c diretti come i vettori
r r r
a, b , c
Tali vettori definiscono la cella unitaria
La cella unitaria è descritta da 6 parametri reticolari
ƒlunghezze dei vettori
r di traslazione:
r
r
a = a ;b = b ;c = c
r r
r r
r r
angoli tra gli assi: α (angolo tra b e c ); β (angolo tra a e c ); γ (angolo tra a e b )
Sette forme differenti di cella unitaria - Sette Sistemi cristallini
Sistema
Lunghezze e angoli
degli assi
Cubico
a = b = c; α = β = γ = 90°
Tetragonale
a = b ≠ c; α = β = γ = 90°
Ortorombico
a ≠ b ≠ c; α = β = γ = 90°
Romboedrico
a = b = c; α = β = γ ≠ 90°
Esagonale
a = b ≠ c; α = β = 90°; γ = 120°
Monoclino
a ≠ b ≠ c; α = γ = 90°; β > 90°
Triclino
a ≠ b ≠ c; α ≠ β ≠ γ ≠ 90°
I reticoli di Bravais
14 reticoli di Bravais
(7 primitivi e 7 centrati)
rappresentano gli unici
14 modi in cui è possibile
riempire lo spazio con un
reticolo tridimensionale
di punti
Struttura cristallina
Per passare dal reticolo alla struttura i punti del reticolo devono essere
occupati da atomi, ioni o molecole
Molecola ABC (motivo che si
ripete) con A coincidente con
l’origine, B e C all’interno della cella
unitaria
A: 0,0,0
B: x1,y1,z1
C: x2,y2,z2
Gli esperimenti di diffrazione forniscono segnali che
corrispondono a piani reticolari
Piani reticolari
Piano interseca gli assi a, b,c nei punti m00, 0n0, 00p
Le coordinate delle intercette sui tre assi (m,n,p) definiscono completamente la
posizione del piano reticolare. Però una delle intercette può essere ∞
Per definire univocamente il piano e evitare indici pari a ∞
si usano i cosiddetti indici di Miller (hkl)
Il piano è in realtà uno dei tanti piani di una “Famiglia” tra loro paralleli e
equidistanti
Il primo piano della famiglia a partire dall’origine intercetta gli assi nei punti
a/h; b/k; c/l dove h,k e l sono gli indici di Miller
Gli indici di Miller (h,k,l) sono dati quindi dal rapporto tra la lunghezza di un
asse e l’intercetta del piano sull’asse stesso
Distanze interplanari
Le distanze interplanari dhkl possono essere espresse in funzione dei
paramentri di cella e degli indici di Miller
La distanza tra l'origine e il piano hkl è dhkl
Applicando la trigonometria possiamo vedere
che valgono le seguenti relazioni:
(a/h) cos α = dhkl
e quindi:
cos α = (h/a) dhkl
analogamente valgono:
cos ß = (k/b) dhkl
cos γ = (l/c) dhkl
Per il reticolo ortorombico
(tutti angoli pari a 90 °):
(cos α) 2+(cos ß )2+(cos γ)2 = 1
quindi:
(h/a)2 d2hkl + (k/b)2 d2hkl + (l/c)2 d2hkl = 1
Per un cristallo cubico:
1/d2hkl = 1/a2 * (h2+k2+l2)
Ortorombico
Tetragonale
Cubico
1
h2 k 2 l 2
= 2+ 2 + 2
2
d hkl a
b
c
1
h2 + k 2 l 2
=
+ 2
2
2
d hkl
a
c
1
h2 + k 2 + l 2
=
2
d hkl
a2
Esagonale
1
4 h 2 + hk + l 2 l 2
=
+ 2
2
2
d hkl 3
a
c
Monoclino
1
h2
k2
l2
cos β
=
+
+
+
2
hl
2
d hkl
a 2 sin 2 β b 2 c 2 sin 2 β
a 2 c 2 sin 4 β
Raggi X
Scoperti da Roengten nel 1895
La lunghezza d’onda dei raggi X è dello stesso ordine di grandezza delle
spaziature tra gli atomi in un cristallo
Si tratta di radiazione ionizzante
I raggi X possono essere prodotti utilizzando
due modi principali :
• Eccitazione di elettroni di core negli atomi
– Questo è il metodo usato nei tubi a raggi X, nei
dispositivi di laboratorio
• Accelerazione di elettroni liberi
– Metodo usato nei sincrotroni
Tubo a raggi X
W
target
X-rays
Vacuum
Come funziona:
Elettroni prodotti da un filamento di
tungsteno riscaldato (catodo)
accelerati da una elevata ddp
Colpiscono il bersaglio (anodo)
costituito da un elemento metallico
Vengono emessi raggi X
Caratteristiche:
Usato in laboratorio
Costo ~ migliaia di Euro
Richiede acqua e alta tensione
• Spettro di
emissione di un tubo
a raggi X
Radiazione bianca (Brehmsstralung)
dovuta al frenamento e perdita di
energia degli elettroni a seguito degli
urti con gli atomi del bersaglio
E max = eV = hv max =
λ min =
hc
λ min
hc 12400
=
eV
V
λ misurato in Å
V misurato in Volts
L’energia massima dei fotoni (e quindi
la minima lunghezza d’onda) dipende
SOLO dall’energia degli elettroni
incidenti ed è indipendente dalla
natura del materiale.
Radiazione caratteristica monocromatica
prodotta quando gli elettroni hanno
energia sufficiente a scalzare un
elettrone da livelli di core
N.B. Radiazione caratteristica compare
solo se si supera una certa tensione di
accelerazione
• Simbologia usata per
indicare la radiazione X
prodotta in un tubo
Kα
2p→1s
Kβ
3p→1s
Kα ha energia minore e intensità maggiore della Kβ
La lunghezza d’onda della radiazione prodotta dipende dal Numero Atomico del
metallo usato come bersaglio
Legge di Moseley
v = k (Z − σ )
ν aumenta e λ diminuisce
All’aumentare di Z
Elementi utilizzati come bersaglio e lunghezza d’onda della radiazione X (Å)
Anodo
Kα1
Kα2
Kα
Cr
2.2896
2.2935
2.2909
Fe
1.9360
1.9399
1.9373
Cu
1.5405
1.5443
1.5418
Mo
0.7093
0.7135
0.7107
Ag
0.5594
0.5638
0.5608
Interazione dei raggi X con la materia
Emissione di fotoelettroni
Fluorescenza
Fascio incidente (I0)
di raggi X
Scattering coerente e incoerente
Assorbimento (I)
calore
Lo scattering coerente dei raggi X è responsabile degli effetti di diffrazione
Gli elettroni diventano sorgenti secondarie di radiazione X
avente la stessa λ della radiazione incidente
La radiazione Kα è quella normalmente utilizzata per gli esperimenti di diffrazione
di raggi X (è la più intensa)
Come eliminare la Kβ e la radiazione bianca?
Il modo più semplice è utilizzare un filtro
I filtri sfruttano la variazione netta del
coefficiente di assorbimento dei raggi X
in corrispondenza di ben precisi valori di
lunghezza d’onda
Anodo
Kα(Å)
Filtro
Cr
2.2909
V
Fe
1.9373
Mn
Cu
1.5418
Ni
Mo
0.7107
Zr
Ag
0.5608
Pd
Il filtro non elimina completamente la radiazione Kβ, che può essere
completamente eliminata usando un cristallo monocromatore (sfrutta la legge
di Bragg
Il fenomeno della diffrazione
La diffrazione è un complesso fenomeno di diffusione (o scattering) e
interferenza originato dall’interazione dei raggi X con un reticolo cristallino.
Il processo di diffusione (o scattering)
L’interazione di un’onda elettromagnetica con la materia avviene essenzialmente
attraverso due processi di scattering:
a) scattering elastico: i fotoni della radiazione incidente vengono deviati
in ogni direzione dello spazio senza perdita di energia.
b) scattering non-elastico: il fotone cede parte della sua energia.
Questo fenomeno non dà luogo a processi di interferenza.
Interazione raggi X con:
Una singola particella
La particella diffonde il
fascio incidente
uniformemente in tutte le
direzioni
Un materiale cristallino
I fasci diffusi si combinano
construttivamente in certe
direzioni
λ/2
Interferenza Costruttiva
Interferenza distruttiva
Diffrazione Raggi X
Il fenomeno della diffrazione è analogo all’interferenza
della luce con un reticolo ottico.
Lungo alcune direzioni (direzione 3) i fasci diffratti A e B
si trovano esattamente sfasati di mezza lunghezza d’onda:
si ha interferenza distruttiva e lungo la direzione 3 si avrà
intensità nulla.
Lungo le direzioni 1 e 2 i due fasci sono in fase e avremo
un massimo di intensità lungo quelle direzioni.
Condizioni di Laue
Max von Laue interpretò la diffrazione di raggi X da parte dei cristalli in analogia con la
diffrazione della luce da parte di un reticolo ottico: la disposizione periodica
tridimensionale degli atomi corrisponde a un reticolo tridimensionale di diffrazione
Partiamo da un reticolo monodimensionale costituito da centri di scattering nei nodi
reticolari
Radiazione S0 incide con angolo di incidenza φ
su un filare monodimensionale.
Radiazione diffratta S forma un angolo θ con
il fascio incidente
Interferenza è costruttiva solo se la differenza di cammino ottico dei raggi
scatterati da due contigui è pari a un multiplo della lunghezza d’onda
Differenza di cammino sul raggio incidente (r), e sul raggio
diffratto (r').
r' - r = a cos(θ) - a cos (φ) = h λ
h numero intero.
In termini vettoriali:
r' - r = a · (S-S0) = h λ
I raggi diffratti giacciono su coni, detti di Laue,
associati ai diversi valori di h.
Il reticolo è tridimensionale per cui
dobbiamo scrivere relazioni analoghe per le altre due direzioni
Condizioni di Laue per la diffrazione:
a . (S-S0) = h λ
b . (S-S0) = k λ
c . (S-S0) = l λ
Le tre equazioni di Laue devono essere contemporaneamente soddisfatte,
la diffrazione avviene solo lungo le direzioni comuni a tre superfici coniche.
L’approccio di Laue seppure corretto è poco pratico (tre equazioni devono
essere soddisfatte contemporaneamente).
Bragg (padre e figlio) immaginarono il fenomeno in termini di riflessione dei
raggi X da parte di piani reticolare infinitamente estesi.
Approccio dei Bragg non è corretto dal punto di vista fisico (il vero fenomeno
che avviene è la diffusione e l’interferenza tra onde diffuse) ma fornisce una
espressione semplice (una unica equazione) e del tutto equivalente alle tre
condizioni di Laue (la direzione del fascio riflesso della legge di Bragg concide
con la direzione che soddisfa contemporaneamente le 3 equazioni di Laue)
Nell’approccio di Bragg i piani reticolari sono immaginati essere semiriflettenti
I raggi X incidono su un pianoe vengono in parte riflessi, in parte trasmessi
La riflessione avviene anche sui piani sottostanti
Interferenza è costruttiva solo se la differenza di cammino tra i raggi riflessi
da piani contigui è pari a un multiplo della lunghezza d’onda
r + r = dhkl sin(θ) + dhkl sin(θ) = n λ
2dhkl sin(θ) = n λ
Legge di Bragg
2dnh nk nl sin(θ) = λ
N.B. La direzione dei fascio diffratto prevista dalle tre condizioni di Laue coincide
con quella prevista dalla legge di Bragg
2d sinθ = λ
d = distanza interplanare
La direzione dei raggi diffratti dipende UNICAMENTE dal reticolo di
traslazione, cioè dai parametri della cella elementare,
indipendentemente dagli atomi che essa contiene
PROPORZIONALITÀ INVERSA TRA sinθ e d
strutture con d grandi mostreranno pattern di diffrazione compressi,
e viceversa per strutture con d piccoli
1/d = (2/λ) sinθ
1/d ∝ sinθ
Esercizio
Un cristallo di Fe (bcc a=2.866 Å) viene sottoposto a un esperimento di
diffrazione di Raggi X utilizzando la radiazione Cr Kα (λ=2.291 Å)
•Calcolare i valori delle distanze interplanari dhkl
•Calcolare gli angoli di Bragg
•Calcolare gli angoli di Bragg usando la radiazione Mo Kα (λ=0.7107 Å)
N.B. in effetti si osservano solo riflessi con h+k+l=2n
A seconda della simmetria del cristallo l’intensità dei segnali è
sistematicamente uguale a zero per certi valori di hkl
Assenze sistematiche nei reticoli centrati
l set di piani P nel caso A produce onde diffratte in fase. Nel caso B dobbiamo
considerare anche la famiglia di piani Q (linee tratteggiate) in posizione
intermedia tra i piani P.
Le onde diffratte dai piani Q saranno fuori fase con quelle riflesse dai piani P,
dando interferenza completamente distruttiva poichè i piani P e Q contengono gli
stessi atomi ed hanno uguale densità
Tecniche sperimentali
L’esperimento di diffrazione di raggi X richiede:
ƒSorgente (tubo o sincrotrone)
ƒStrumenti di laboratorio usano tubo a raggi X
ƒCampione (monocristallo o polvere)
ƒMonocristallo (o cristallo singolo) più adatto per l’analisi strutturale
ƒCampione policristallino più semplice usato soprattutto per analisi
qualitativa e quantitativa
ƒRivelatore (lastra fotografica o metodi a contatore)
ƒMetodi a lastra fotografica hanno solo interesse storico, ma oggi si
usano anche contatori bidimensionali che forniscono pattern di
diffrazione molto simili a quelli delle lastre fotografiche
Rivelatori per Raggi X usati in diffrazione
Film fotografico: elevata accuratezza risolutiva, ma scarsa accuratezza nella
misura dell'intensità.
Scintillatore: Materiale che emette luce quando irradiato con raggi X. Un
fotomoltiplicatore rivela la luce e emette un pulso. Accurata misura delle
intensità ed delle posizioni, difetto di poter misurare una sola intensità
diffratta alla volta
Rivelatori CCD (Charged Couple Device)
Rivelatore bidimensionale a stato solido e di tipo quantico La stessa
"simultaneità" di una lastra, con migliore misura delle intensità diffratte.
Peccano in potere risolutivo, a causa delle dimensioni dei chip.
Diffrazione di raggi X su campioni policristallini
Se idealmente il numero di particelle cristalline in diffrazione è molto elevato e
tutte le possibili orientazioni sono ugualmente rappresentate, allora ciascun piano
cristallografico origina un insieme di linee contigue che formano la superficie di un
cono di diffrazione
Camera di Debye
Si originano contemporaneamente i
fasci diffratti per diverse famiglie di
piani. Per ciascuna famiglia di piani i
fasci diffratti si trovano su un cono che
tagliano la lastra fotografica su una
coppia di archi
Diffrattometri per polveri (campioni policristallini)
Si varia con continuità e sincronicamente l’angolo tra fascio incidente e campione
e quello tra campione e rivelatore
Geometria di Bragg-Brentano
Con questa geometria, il campione è sempre in una precisa posizione "focalizzata",
che viene preservata cambiando simultaneamente l'angolo incidente e quello di
rivelazione (θ-θ, con sorgente mobile e campione fisso), oppure variando
opportunamente l'orientazione del campione e l'angolo di rivelazione (ω-2θ).
Geometria Bragg-Brentano con monocromatore su fascio diffratto
Intensità (conteggi/sec)
200
150
100
50
0
10
20
30
40
50
2θ
60
70
80
90
Quantità osservabili
ƒPosizione dei picchi
ƒIntensità dei picchi
ƒForma dei picchi
ƒFondo sottostante i picchi
Posizione dei picchi: Dipende esclusivamente dalla cella elementare del
materiale in esame. E possibile dai dati di polveri determinare e affinare le
costanti di cella con elevata precisione. Su questo dato viene in gran parte
basata il riconoscimento di fasi incognite
Intensità dei picchi: L'intensità diffratta si ottiene integrando l'area di
ciascun picco, dopo aver sottratto il contributo di fondo. Una misura
approssimata si ottiene dal massimo valore dei conteggi di ciascun picco.
Le intensità diffratte da ciascuna fase presente in una miscela di un campione
polifasico sono proporzionali alla frazione di quella fase.
La forma del picco e fattori che la influenzano
I fattori che influenzano la forma del picco sono:
STRUMENTALI: divergenza del raggio incidente e/o del raggio diffratto;
risoluzione del rivelatore e modalità di scansione del picco; dimensioni del campione.
DEL CAMPIONE: mosaicità delle particelle cristalline e loro dimensione, oppure
possibili deformazioni (stress ecc.).
Per quanto riguarda la dimensione delle particelle, vale la relazione di DebyeScherrer:
dove K è una semplice costante di proporzionalità e D è la dimensione media
delle particelle.
Procedura sperimentale
•selezione del campione (microcristallinità)
•macinazione per migliorare l’omogeneità riducendo le dimensioni delle
particelle (ma non troppo per evitare l’allargamento dei picchi)
•deposizione del campione su supporto
•centratura del supporto nel goniometro
•scansione (selezionando il tipo di scansione, la velocità ecc.)
Analisi qualitativa
L’analisi qualitativa si riferisce alla identificazione di fasi presenti in miscele
oppure al riconoscimento di fasi a componente singolo.
co-presenza di più fasi
Se in un campione policristallino
esistono più fasi, la diffrazione da
polveri conterrà picchi corrispondenti a
distanze interplanari di tutte le fasi
La struttura cristallina di molte fasi solide è nota, perché identificata con
metodi diffrattometrici a partire dalla introduzione di queste tecniche, cioè a
partire dalla prima metà del XX secolo.
La principale "risorsa" di informazioni per l’identificazione di fasi ignote è il
Powder Diffraction File, ossia un archivio elettronico (o cartaceo) dove sono
contenute informazioni cristallografiche per più di 300000 fasi inorganiche
ed organiche.
La diffrazione è una informazione primaria, che combinata con l’analisi
elementare identifica senza ambiguità una certa fase cristallina.
Dai valori angolari a cui si osservano i riflessi di Bragg è possibile ottenere le
informazioni sulla forma e dimensione della cella unitaria
Occorre attribuire gli indici di Miller ai segnali di diffrazione osservati, e
utilizzare le formule che legano le distanze interplanari alle alle costanti
reticolari e agli indici di Miller
Il caso più semplice è quello del reticolo cubico
2d hkl sin(θ hkl ) = λ
d hkl =
a
h +k +l
2
2
2
sin (θ 2 ) h2 + k 2 + l2
=
2
2
2
2
sin (θ1 ) h1 + k1 + l1
2
2
2
2
2d hkl sin(θ hkl ) = λ
d hkl =
a
h2 + k 2 + l 2
sin 2 (θ 2 ) h2 + k 2 + l2
= 2
2
sin (θ1 ) h1 + k12 + l12
2
2Θ
dhkl
sen2
28,45
3,13
0,06
47,31
1,92
0,16
56,12
1,64
69,13
sen2/
sen2
h2+k2+l2
2
h2+k2+l2
2
hkl
2,00
3,00
111
2,66
5,33
7,99
220
0,22
3,66
7,33
10,99
311
1,36
0,32
5,33
10,66
15,99
400
76,37
1,25
0,38
6,33
12,65
18,98
331
88,03
1,11
0,48
7,99
15,99
23,98
422
94,94
1,04
0,54
8,99
17,98
26,97
333
Esercitazioni di Laboratorio – Diffrazione di Raggi X
1. Raccolta pattern di diffrazione di polveri di varie sostanze
•
Fasi singole con struttura cubica (NaCl, KCl, Fe, Al, …):
indicizzazione del pattern e determinazione delle costanti di cella e
della densità
•
Fasi singole a struttura non cubica: determinazione delle costanti di
cella
•
Miscele di più fasi: analisi qualitativa
2. Uso software cristallografico
•
Analisi pattern diffrazione: software ANALYZE. Determinazione
delle posizioni dei picchi, del fondo e delle intensità. Analisi
qualitativa con e senza informazione chimiche
•
Banca dati PDF-2: software PCPDFWIN per recuperare le Card
delle fasi desiderate.
Raccolta pattern di diffrazione
•macinazione polveri (l’omogeneità)
•deposizione delle polveri sul portacampione (la superficie della polvere deve
essere liscia e a filo con la superficie del portacampione)
•centratura del portacampione nel diffrattometro
•scansione (selezionando il tipo di scansione, l’angolo iniziale e finale, la velocità
ecc.)
Indicizzazione pattern fasi cubiche
2d hkl sin(θ hkl ) = λ
d hkl =
a
h2 + k 2 + l 2
sin (θ 2 ) h2 + k 2 + l2
= 2
2
sin (θ1 ) h1 + k12 + l12
2
2
2Θ
dhkl
sen2
28,45
3,13
0,06
47,31
1,92
0,16
56,12
1,64
69,13
sen2/
sen2
h2+k2+l2
h2+k2+l2
hkl
2,00
3,00
111
2,66
5,33
7,99
220
0,22
3,66
7,33
10,99
311
1,36
0,32
5,33
10,66
15,99
400
76,37
1,25
0,38
6,33
12,65
18,98
331
88,03
1,11
0,48
7,99
15,99
23,98
422
94,94
1,04
0,54
8,99
17,98
26,97
333
2
2
Determinazione costante di cella
a (Å) = d hkl (Å) h + k + l
2
2
2
Per ciascun riflesso otteniamo la costante di
cella. Δd/d diminuisce con l’angolo θ
Determinazione densità
n × PF ( g / mole) × 10 (Å / cm )
D ( g / cm ) =
3
23
−1
a (Å) × 6.022 × 10 (mol )
3
24
3
3