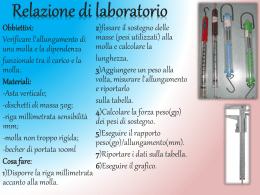
VERIFICA DELLA LEGGE
DI HOOK
E MISURA DELLA
COSTANTE ELASTICA
DI UNA MOLLA
In figura sono rappresentate delle
molle disposte verticalmente e con l’
estremo superiore collegato ad un
supporto fisso. Se all’ altra estremità
viene sospesa una massa m si
osserva che la molla si allunga. L’
allungamento è proporzionale al peso
della massa m.
L’ esperimento consiste nel verificare
la legge di Hook e in condizioni
statiche e dinamiche misurare la
costante elastica della molla.
Nella condizione statica la massa è in
equilibrio sotto l’ azione della forza
peso e della forza elastica esercitata
dalla molla deformata.
Nella condizione dinamica, che si
osserva quando la molla gravata dalla
massa m è di poco allungata e poi
lasciata libera, il sistema massa-molla
oscilla. Dimostreremo che il moto è
armonico semplice e che il periodo
delle oscillazioni dipende da m e dalla
costante elastica della molla
♦
.
BOZZA
prof. M. Calicchio
1
CONDIZIONE STATICA
All’ estremo libero della molla viene agganciato un cestello
contenente dei piombini. La massa m è in equilibrio sotto l’
azione di due forze aventi la stessa direzione e verso
opposto ossia il suo peso e la forza esercitata dalla molla.
l0
x
P + Fk = 0
Per verificare la legge di Hook, ossia che la forza di
richiamo elastica è proporzionale alla deformazione della
molla, è sufficiente caricare la molla con diversi pesi p e per
ognuno di essi misurare il relativo allungamento x. La
legge Hook sarà sperimentalmente verificata se di i punti di
coordinate (xi,pi) si dispongono secondo linea retta la cui
pendenza è la costante elastica della molla, normalmente
indicata con K.
Le misure fatte saranno tanto più precise quanto più i punti
di coordinate (xi,pi) stanno su una retta.
L’equazione che otterremo F = −Kx è valida per carichi
non eccessivi superati i quali l’ andamento non è più lineare
e la molla tenderà prima a snervarsi e poi a spezzarsi.
La costante elastica della molla dipende dal tipo di materiale
usato, dal diametro del filo, dal diametro delle spire oltre che
dal processo di lavorazione meccanica. ♦
y = 11,59x + 0,009
graf1
R2 = 0,9997
3,00
2,50
2,00
P (N)
Nel grafico la rappresentazione
di 6 punti (xi,pi) relativi ad un set
di misure. Sul grafico in rosso l’
equazione della retta di fit
lineare, la cui pendenza è K.
1,50
1,00
0,50
0,00
0,00
0,05
0,10
0,15
0,20
0,25
x (m )
Bozza
Prof. M. Calicchio
2
CONDIZIONE DINAMICA
Supponiamo di abbassare ulteriormente la
molla di xA e quindi di lasciarla libera.Il
sistema massa+molla inizia ad oscillare, il
centro delle oscillazioni che dimostreremo di
ampiezza xA è indicato dalla freccia in blu e
corrisponde al punto di equilibrio delle forze.
Dalla seconda legge di Newton:
lo
R = p + Fk = m a
o
x
xA
x
C entro di
oscillazione
posto
otteniamo
m
k
2
k
d x*
− x* = 2
m
dt
x* = x − g
x *' = Asen(Ωt + ϕ)
poiché
(1)
Nel sistema di riferimento della figura,
ponendo Fk = - K x possiamo scrivere
d2 x
mg - kx = m 2
dt
dove con m indichiamo la massa con cui è
gravata la molla. L’ equazione è quindi valida
solo nel caso ideale in cui si considera
trascurabile la massa della molla.
Questa è una equazione differenziale del
secondo ordine, lineare, non omogenea, con
il termine noto costante che può essere
ricondotta, con una sostituzione di variabili, a
una dello stesso tipo ma omogenea già vista
per esempio nel caso del pendolo semplice.
Infatti dividiamo per m e mettiamo in
evidenza – k/m
k
m
d2 x
− (x − g ) = 2
m
k
dt
dx * dx
=
dt
dt
e
d2 x * d2 x
= 2
d2 t
dt
equazione questa che ha una soluzione del tipo:
(2)
dove A è l’ ampiezza del moto, ϕ la fase iniziale ed entrambe sono delle costanti non note a
priori ma da determinare in base alle condizioni iniziali del moto; (Ωt + ϕ) è la fase, Ω
pulsazione che dipende dai valori di m e k♦.
Bozza
prof. M. Calicchio
3
Calcoliamo della equazione(2) la derivata prima e seconda
d 2 x *'
dx *'
= − Ω 2 Asen ( Ω t + ϕ ) e sostituiamole nella (1)
= ΩA cos(Ωt + ϕ )
2
dt
d t
k
− Asen ( Ω t + ϕ ) = − Ω 2 Asen ( Ω t + ϕ ) che risulterà soddisfatta se
m
k
m
= Ω2
e quindi
T = 2π
m
k
la soluzione è:
m
x = Asen(Ωt + ϕ) + g
che rappresenta un moto armonico, con il centro di oscillazione
k
m
x = g che è la posizione di equilibrio del sistema ossia la posizione in cui forza peso e forza
k
elastica hanno risultante nulla.
Determiniamo A e ϕ.
Nel nostro caso allungata ulteriormente la molla la rilasciamo con velocità iniziale nulla. A
m
t=0
sarà v 0 = 0
x0 = x A + g
e quindi
k
π
0 = ΩA cos ϕ
in questa equazione non sono nulli né Ω né A per cui ϕ =
2
m
m
π
= Asen + g
da cui risulta che l’ ampiezza della oscillazione A è proprio xA.
k
2
k
Possiamo riscrivere l ‘ equazione in forma più compatta
m
m
π
π
π
x = x A sen(Ωt + ) + g = x A senΩt cos + x A cos Ωtsen + g
2
k
2
2
k
m
x = x A cos Ωt + g
k
xA + g
Da osservare che l’ equazione da noi ricavata è rigorosamente valida nel caso ideale in cui la
molla abbia massa nulla, sia perfettamente elastica e siano trascurabili gli attriti. Si può
dimostrare che tenendo conto della massa della molla il periodo diventa
T = 2π
m + mk / 3
K
per cui se la massa della molla mk non è trascurabile rispetto a quella di carico il periodo
misurato è maggiore di quello atteso per il caso in esame e di ciò bisogna tener conto nella
interpretazione dei dati sperimentali♦.
Bozza
prof. M. Calicchio
4
La misura dinamica della costante elastica della molla va quindi fatta misurando il periodo di
oscillazione, dalla relazione
T2
riscritta come m = K 2
nella formula T è il valore medio per il
4π
set di 30 misure corrispondenti al valore di massa usata
m
T = 2π
k
possiamo ottenere delle coppie di valori ( (
linea retta la cui pendenza è K.
Ti2
, m) che graficati dovrebbero disporsi su una
4π 2
graf3
Il grafico 3 mostra l ‘
andamento
dei
dati
sperimentali e riporta l’
equazione della retta di fit
lineare la cui pendenza è K.
Può essere interessante
valutare se il valore ottenuto
per la costante elastica da
misure di periodo dipenda o
no dalla massa della molla.
y = 11,656x - 0,0064 R2 = 0,9998
0,30
0,25
m (Kg)
0,20
0,15
0,10
0,05
0,00
0,00
0,01
0,01
0,02
0,02
0,03
T*T*0,101 (sec*sec)
Graf 2
andamento di k in funzione di p
12,5
12,0
k
11,5
11,0
10,5
k vs p
k corretta vs p
10,0
0,5
1,0
1,5
2,0
p
2,5
3,0
Nel grafico 2 sono plottati i
valori medi di K in funzione
del
peso
di
carico
utilizzando per il calcolo di k
solo la massa del carico
(puntini e linea blu) e
rifacendo
i
calcoli
correggendo per la massa
della molla (puntini e linea
rossa).
Si nota che la correzione
usata mk/3, che forse è
eccessiva, fa aumentare il
valore di K in misura
maggiore per piccoli carichi.
I dati mostrano una evidente
convergenza per valori di m
>>
mk/3
ovvero
in
condizione ideale di massa
della molla trascurabile♦
Bozza
prof. M. Calicchio
5
COME FARE LE MISURE
La figura mostra la molla ed il cestello inseriti nello
strumento MITE che misura i tempi e ha 11
Trasmettitori e 11 Ricevitori di cui in questa misura va
attivata una sola coppia.
La coppia T-R che bisogna attivare deve essere a ≅1
cm al di sotto del cestino in modo che quando esso
oscilla sia alternativamente completamente oscurata e
non. Al crescere della massa nel cestino la molla si
allunga e l’ oscillazione interesserà la coppia T-R
sottostante. Lo studente deve quindi disattivare la
coppia precedente ed attivare la successiva
spostando un piccolo “jumper” ( ponticello ) situato
sulla sinistra dello strumento in corrispondenza del
ricevitore, nella figura le coppie attivate sono in
arancione e quelle disattivate in blu. La manovra va
fatta con delicatezza per evitare di spezzare i contatti.
Poiché le fotocellule sono distanziate di 4 cm la coppia
attivata potrebbe non essere nella posizione corretta;
la vite di registrazione in alto sullo strumento ha una
corsa di 4 cm e permette di avere una regolazione fine
di posizione. Se si usa questa regolazione accertarsi
che i bulloni di bloccaggio siano ben stretti.
Lo studente ha a disposizione dei piombini di varie
misure e con essi deve caricare il cestello. Mescolare
piombini medi, piccoli e piccolissimi in modo che la
massa sia stabile durante le oscillazioni. Iniziare le
misure con una massa di piombini di almeno 100 gr
perché per masse inferiori facilmente il sistema
ballonzola in quanto prossimo a condizioni di
risonanza.
La massa dei piombini e del cestello va misurata
utilizzando la bilancia ad un piattello della figura. La
bilancia ha due scale 0-100gr e 0-500gr. La scala si
seleziona portando in alto o in basso un dischetto
fissato ad un’ asta ruotante. La sensibilità della
bilancia è di 1gr, che però non è apprezzabile sulla
scala 0-500gr. La vite di regolazione in basso a
sinistra va usata per mettere in piano la bilancia e
regolare la posizione di zero. Fare accuratamente le
misure evitando nei limiti del possibile errori di
parallasse♦.
Bozza
prof. M. Calicchio
6
Per misurare la lunghezza della molla utilizzare la riga a disposizione che va messa in
verticale e a squadro.
I valori letti min e max della figura vanno annotati ed inseriti nel foglio di excel nelle apposite
celle insieme al corrispondente valore misurato per la massa. Le misura della lunghezza a
riposo della molla e quella del gancio e cestello vanno fatte una sola volta ed i valori vanno
inseriti nel foglio di lavoro.
Dopo aver misurato massa e lunghezza mettere in oscillazione il sistema tirando
delicatamente il cestello verso il basso lungo la verticale.
Attivare quindi il programma di acquisizione dei tempi e aquisire i periodi di almeno 30
oscillazioni. Se i periodi misurati sono in misura superiore selezionarne 30 e inserirli nel foglio
di lavoro; nel programma di acquisizione usare lo ‘scroll’ per vedere misure superiori a 16.
Ripetere la procedura 6 volte aumentando la massa ogni volta di ≅ 30 gr e registrare con un
nome a scelta il file dei dati che conviene poi inserire simultaneamente nel foglio di lavoro.
Il foglio excel è organizzato per riquadri, uno per ogni misura. Per una comprensione più
immediata i calcoli, prevalentemente delle medie, sono illustrati da commenti e formule inserite
in modo non attivo.
Qui di seguito come acquisire i dati ed importarli in excel
7
come acquisire i dati
Accendere il computer, l’ apparato di misura.
Sulla scrivania del p.c. appaiono varie icone tra cui quella di “PT-Bat” su cui
bisogna puntare il mouse e “cliccare” 2 volte con il tasto sinistro. Sullo schermo
appare un menù con diverse opzioni, che vengono selezionate con le frecce in
su e in giù della tastiera ed attivate premendo “ enter”.
1a schermata:
selezionare M- motion timer
Precision Timer (MS-DOS Version)
Copyright 1988-1992 Vernier Software
SELECT MODE:
M - Motion Timer
G - Gate Timing Modes
P - Pulse Timing Modes
K - Keyboard Timing Modes
C - Collision Timer
T - Miscellaneous Timing Modes
D - Data Analysis Options
O - Other Options
S - Photogate Status Check
Q - Quit
---------------------------------------Type letter or use the arrow keys,
then press <Enter>.
8
2a schermata:
un leggero sibilo e i due puntini dicono che il sistema è pronto ad acquisire. Lasciare
libero il contenitore e quindi exit
Motion Timer
Timing will begin when photogate #1 is first blocked
.:
press <Enter> to exit
3a schermata:
appaiono i tempi misurati ( ∆t1, ∆t2,.. in unità di sec )
PRECISION TIMER
Motion Timer
11
1
11 , 0 , 0 , 0 , 0 , 0 , 0
TIME
s
ROW #
ROW "TIME 1"
1 , .08746629
2 , .037699268
3 , .028224584
4 , .02413551
5 , .021542439
6 , .019248568
7 , .017752565
8 , .016555763
9 , .015658161
10 , .014561093
11 , .013862958
EOF
_________________________________________________
9
4a schermata:
selezionare
D - Data Analysis Options
Precision Timer (MS-DOS Version)
Copyright 1988-1992 Vernier Software
SELECT MODE:
M - Motion Timer
G - Gate Timing Modes
P - Pulse Timing Modes
K - Keyboard Timing Modes
C - Collision Timer
T - Miscellaneous Timing Modes
D - Data Analysis Options
O - Other Options
S - Photogate Status Check
Q - Quit
---------------------------------------Type letter or use the arrow keys,
then press <Enter>.
5a schermata:
selezionare
F - File Options
DATA ANALYSIS OPTIONS - "Motion Timer" Mode
SELECT OPTION:
T - Display Table of Data
P - Print Table of Data
L - Large Digit Data Table
D - Delete Data
F - File Options
G - Graph Data
X - Return to Main Menu
---------------------------------------Type letter or use the arrow keys,
then press <Enter>.
10
6a schermata:
selezionare
S - Save Data to a File e assegnare il nome al file;
oppure far precedere da C - Change the Current Directory se si vuole cambiare la dir che di default è CURRENT
DIRECTORY: C:\…………….. \ACQ-SAVE\DIDATTIC\TIMER
SELECT OPTION:
D - Contents of Current Directory
L - Load Data from a F ile
S - Save Data to a File
C - Change the Current Directory
M - Make a New Directory
E - Erase a Data File
X - Return to Data Analysis
---------------------------------------Type letter or use the arrow keys,
then press <Enter>
N.B.
i
dati
di
misura
automaticamente
salvati
nella
cartella
…./didattic/timer/dummy con il nome dummy. E’ possibile cambiare la cartella di
destinazione del file dummy attivando l’ opzione C.
In appendice B: come importare i dati in excel ed elaborarli
11
Aprire sul desktop il file di excel predisposto
Dal menù file scegliere ‘ apri ‘ e quindi selezionare
la cartella ed il nome del file.
Appaiono le seguenti icone
selezionare larghezza fissa e quindi avanti
12
delimitare con le frecce il campo e quindi avanti
selezionare avanzate e quindi avanti
13
selezionare separatore decimale punto e
separatore delle migliaia nessuno
e quindi OK. E’ evidenziata la porzione di dati da copiare. Chiudere il
file dei dati e incollare gli appunti nel programma di analisi.
I dati copiati negli appunti vanno trasferiti nelle relative colonne di excel
14