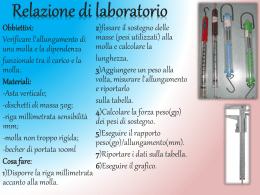
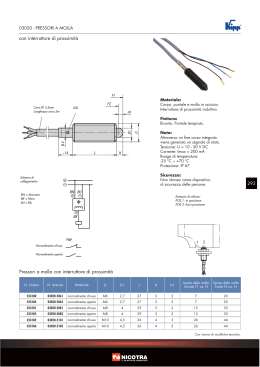
Figura 1:
h
A
R
Figura 2:
1
h
2
Energia e Lavoro
Es. 1
Calcolare la velocità di fuga dal pianeta Giove. sapendo che ha una massa m = 1.89 · 1027 kg, un volume
V = 1.43 · 1024 m3 e ricordando che G = 6.67 · 10−11 m3 kg −1 s−2 .
Es. 2
Quando una massa m1 = 4 kg è appesa ad una molla di massa trascurabile, che obbedisce alla legge di Hooke,
la molla si allunga di 2.5 cm. Se si toglie la massa m1 , di quanto si allungherà la molla se si appende una massa
m2 = 1.5 kg? Quanto lavoro deve compiere un agente esterno per allungare la stessa molla di 4 cm dalla sua
posizione di equilibrio?
Es. 3
Un blocco di 12 kg, partendo da fermo, scivola giù lungo un piano liscio, inclinato di 35◦ , percorre 3 m e viene
fermato da una molla di costante elastica k = 3 · 104 N/m. Di quanto la comprime?
Es. 4
Vedere Fig. 1. Una sferetta scivola senza attrito lungo la guida in figura. Se la sferetta viene lasciata andare
da un’altezza h = 3.5 R, qual è la velocità v in A in funzione di R? E quanto vale la forza normale N agente
sulla sferetta se la sua massa è di 5 g?
Es. 5
Vedere Fig. 2. Due masse sono collegate da una fune ideale che scorre su una carrucola ideale. Sappiamo
che m1 = 5 kg e m2 = 3 kg; m1 viene lasciata andare da ferma da un’altezza hi = 4 m. Usando le leggi
di conservazione dell’energia, si determini la velocità v della massa m2 nell’istante in cui m1 tocca il suolo e
l’altezza hmax a cui salirà m2 .
Es. 6
Vedere Fig. 3. Un blocco di massa m = 0.25 kg è posto su una molla verticale con k = 5000 N/m ed è
premuto verso il basso in modo da comprimere la molla di δx = 0.1 m. Dopo essere stato lasciato libero, da fermo, esso si sposta verso l’alto e poi abbandona la molla. A quale altezza h giunge al di sopra del punto di rilascio?
Es. 7
Vedere Fig. 4. Il coefficiente di attrito tra un oggetto di 3 kg (m1 ) e la superficie è µ = 0.4. Entrambe le masse
partono da ferme. Qual è la velocità v della massa da 5 kg (m2 ) quando è scesa di un tratto lungo L = 1.50 m?
1
Figura 3:
h
Figura 4:
1
2
L
2