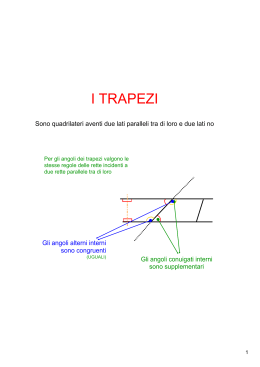
le proprietà dei
quadrilateri
l’equivalenza
Occhio a errori
o
imprecisioni…
il calcolo dell’area
iprof
I QUADRILATERI
Un quadrilatero è una figura geometrica
piana che ha quattro lati e quattro angoli
D
A
C
B
D
C
A
B
In un quadrilatero la somma degli angoli
interni è uguale a due angoli piatti, cioè a 180°
Il perimetro si calcola addizionando tutti i lati
P = AB + BC + CD + AD
I QUADRILATERI
TRAPEZIO
PARALLELOGRAMMA
RETTANGOLO
ROMBO
QUADRATO
IL TRAPEZIO
 Il trapezio è un quadrilatero che ha due lati
opposti paralleli
base minore
D
lato obliquo
A
C
altezza
base maggiore
lato obliquo
B
C
D
B
A
Gli angoli adiacenti ad uno stesso lato sono
supplementari
ˆ ˆ
ˆ ˆ
A + D = 180° B + C = 180°
Il trapezio può essere:
ISOSCELE
C
D
A
B
H
 i lati obliqui sono uguali
K
AD = BC
 gli angoli adiacenti a ciascuna base sono uguali
ˆ ˆˆ ˆ
A=B D=C
 Le proiezioni dei lati obliqui sulla base maggiore sono
uguali
AH = KB
Il trapezio può essere:
D
RETTANGOLO
C
A
B
 ha un lato perpendicolare alle basi
AD
AD
AB
DC
quindi ha due angoli retti
Il trapezio può essere:
D
SCALENO
C
A
 i lati obliqui sono disuguali
B
IL PARALLELOGRAMMO
D
C
altezza
A
B
H
Il parallelogrammo è un quadrilatero che ha i lati
opposti paralleli e uguali
• gli angoli opposti sono uguali
ˆ ˆˆ ˆ
A=C B=D
• gli angoli consecutivi sono supplementari
• le diagonali si dimezzano scambievolmente
IL RETTANGOLO
D
C
altezza
A
B
base
Il rettangolo è un parallelogrammo che ha
quattro angoli retti
 le diagonali sono uguali e ciascuna di esse divide il
rettangolo in due triangoli rettangoli
P=(b+h)x2
b=P:2–h
h=P:2-b
IL ROMBO
D
Il rombo è un parallelogrammo
con i quattro lati uguali
• le diagonali sono perpendicolari
C e si tagliano scambievolmente a
metà
A
• gli angoli opposti sono uguali
ˆA = Cˆ ˆB = ˆD
B
P = l x4
l =P:4
IL QUADRATO
Il quadrato è un
parallelogrammo che ha
i lati uguali e tutti gli
angoli retti
D
C
A
B
 le diagonali sono uguali, perpendicolari e si
tagliano scambievolmente a metà
 il quadrato è l’unico quadrilatero regolare
P = l x4
l =P:4
L’equivalenza
Le figure precedenti si possono scomporre
nelle stesse figure più piccole, quindi sono
equiscomponibili.
Figure equiscomponibili occupano la stessa
superficie, quindi sono equivalenti, cioè hanno
la stessa area
Impariamo a calcolare le aree dei
quadrilateri
 rettangolo
quadrato
 parallelogrammo
 rombo
 trapezio
altezza
=u2
base
L’area del rettangolo si calcola:
A=bxh
IL RETTANGOLO
IL QUADRATO
= u2
Il quadrato è un rettangolo
particolare in cui
base = altezza = lato
lato
quindi
A = l x l = l2
IL PARALLELOGRAMMO
altezza
base
Il parallelogrammo è equivalente ad un
rettangolo che ha la stessa base e la stessa
altezza, perciò la sua area si calcola:
A=bxh
IL ROMBO
diagonale
diagonale minore
maggiore
Il rombo è equivalente
ad un rettangolo che
ha per base la
diagonale minore e per
altezza la metà della
diagonale maggiore,
quindi:
A=Dxd
2
IL TRAPEZIO
base minore
+ base maggiore
altezza
+ base minore
Il trapezio è equivalente alla metà di un parallelogrammo
che ha la stessa altezza e per base la somma delle basi
del trapezio, quindi
base maggiore
A=B+b
2