Apparato per la misura dell’effetto Hall
in un semiconduttore drogato P a varie temperature
Introduzione
L'effetto Hall è importante nello studio delle caratteristche dei materiali perchè permette
di misurare direttamente la concentrazione dei portatori di carica liberi ed il segno della
loro carica sia nei metalli che nei semiconduttori.
E’ altresì tecnologicamente importante perchè sta alla base del funzionamento dei
moderni sensori per misure di campo magnetico.
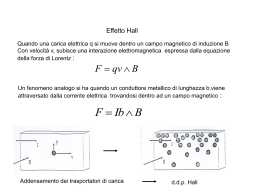
L’effetto Hall è essenzialmente una manifestazione della forza di Lorentz F che agisce
su ogni carica elettrica q che si muova con
v in un campo magnetico B.
! velocità
! !
F = qv ! B
1
Consideriamo un tratto di conduttore di forma parallelepipeda (figura 1) immerso in un
campo magnetico B uniforme diretto secondo l’asse z, percorso da una corrente elettrica
di intensità Ix secondo x.
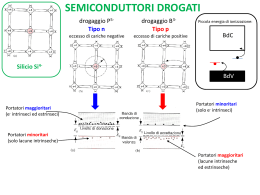
Nei metalli la corrente elettrica è trasportata solo da elettroni. Nei semiconduttori invece
i portatori di carica elettrica possono essere sia elettroni che lacune. In un
semiconduttore puro la densità di elettroni n e di lacune p è la stessa, nei semiconduttori
drogati invece si ha n>>p (in materiale di tipo N) oppure p>>n (in materiale di tipo P).
Nel caso di metalli o semiconduttori drogati quindi è importante solo un tipo di portatori
di carica (per elettroni q=-e , e per lacune q=+e).
Figura 1: Geometria dell’effetto Hall: la forza di Lorentz FL sulle cariche in moto (sia di segno positivo
che negativo) si sviluppa nella direzione indicata
Gli elettroni acquistano una velocità di deriva vd = µ Ex sotto l’effetto del campo
elettrico Ex (e nel verso contrario ad esso). La forza di Lorentz FL = q vd B, agisce sugli
elettroni nel verso delle y negative e quindi essi tendono ad accumularsi sulla faccia del
campione perpendicolare all’asse y e posta verso chi guarda la figura 1.
Questo accumulo di cariche porta alla formazione di una differenza di potenziale VH fra
le due facce del campione perpendicolari all’asse y, e quindi di un campo elettrico EH
(campo di Hall) tale che la forza elettrica qEH sia uguale ed opposta alla forza di
Lorentz:
EH = vd B.
Conviene perciò definire il coefficiente di Hall come
RH = EH/(JxB).
Ricordando che Jx = -envd (oppure Jx = +epvd)si ha :
RH = vdB/(Jx B) = -1/(en) [oppure = +1/(ep)]
[1]
a seconda che si tratti di lacune o di elettroni.
2
In conclusione la misura di RH ci dà direttamente la concentrazione n dei portatori liberi
! ! !
ed il loro segno (se si è in grado di stabilire la direzione dei vettori B, J, E H .
Nel ricavare la formula (1) si è assunto che le velocità di tutti i portatori siano identiche.
Se si tiene conto che in realtà c’è una distribuzione statistica delle velocità e dei tempi
medi di collisione si arriva ad una espressione che differisce dalla (1) per un fattore
numerico r che può assumere valori da 3π/8 ≈ 1.18 a ≈ 2 :
RH = r /(n q)
Il coefficiente di Hall dei semiconduttori è di molti ordini di grandezza maggiore di
quello dei metalli, dato il numero molto minore dei portatori di carica liberi.
Per questo motivo l'esperimento con i semiconduttori è più facile: richiede correnti di
polarizzazione dei campioni solo dell'ordine dei mA e dà tensioni di Hall già dell'ordine
dei mV misurabili direttamente senza la necessità di grande amplificazione.
Per ottenere RH occorre misurare VH, Ix , B e lo spessore t del campione dato che :
RH = EH/(BJx) = (VH/s)/(BIx/ts) = VH t/(B Ix)
[2]
E’ importante notare che il verso della forza di Lorentz Lorentz non dipende dal segno
del portatore e agisce quindi nello stesso verso sia per portatori negativi che per
portatori positivi.
L'espressione generale di RH, valida nel caso generale (cfr. Appendice) in cui si abbiano
sia elettroni che lacune con concentrazioni rispettivamente n e p e mobilità µe e µh è:
pµ 2h ! nµ 2e
[3]
RH = r
e( pµ h + nµ e )2
che si riduce alla [1] non appena p>>n o n>>p.
Per un semiconduttore abbastanza drogato µH coincide, a meno del fattore numerico r,
con la mobilità di deriva dei portatori maggioritari µ H = R H σ ≈
r
(e p µh) = r µh
pe
Poiché aumentando la temperatura si creano molti portatori intrinseci, cioè coppie
elettrone-lacuna, un campione drogato P, che a temperatura ambiente dà un RH
positivo, a temperature più alte dà un RH decrescente che può diventare zero e cambiare
di segno, dal momento che il rapporto tra le mobilità b=µe /µh è maggiore di 1 (vale
circa 1.5). Ciò non avviene con un campione drogato N.
Dalle misure di RH e della resistenza in funzione di T si possono ottenere stime di molti
parametri.
Dai valori di R si passa facilmente alla conducibilità elettrica:
σ = l/(RS),
dove l è la lunghezza ed S la sezione del campione, ed al coefficiente di Hall
Il prodotto RHσ, noto come mobilità di Hall, coincide col valore µh = 0.19 m2V-1s-1
della mobilità di deriva delle lacune a temperatura ambiente moltiplicato per r ≈ 1.2.
3
Dalla relazione [3] si vede che quando RH =0 (“punto di inversione”, che avviene in
zona intrinseca) si ha nb2=p, ove p=Na+N e n=N, indicando con N la densità di coppie
in zona intrinseca.
La conducibilità al punto di inversione vale σo = e(nµe+pµh ) = e(Nµe+[Na+N]µh)=
e[N(µe+µh)+ Naµh] = eµh [N(b+1)+ Na].
Se invece si estrapola la conducibilità dalla regione estrinseca (ove la densità di
portatori è costante N= Na) si ottiene il valore σe = e pµh = eNa µh.
Per estrapolare la conducibilità (o il suo reciproco, resistività ρ) si può assumere una
legge di potenza per la mobilità del tipo µ(T)= cost Tα, con esponente α negativo, da
determinarsi sperimentalmente.
Il valore della conducibilità σe estrapolato dalla zona estrinseca, una volta stimata µh,
fornisce una stima di Na = σe/eµh .
Inoltre si ha Na/N= b2-1.
Con qualche rielaborazione si ottiene per il rapporto σo/σe=ρe/ρo = b/(b-1) , relazione
che consente di ricavare dai dati sperimentali il valore di b=Re/(Re-Ro).
Dal valore di b si ottiene poi una stima della densità N di portatori intrinseci al punto di
inversione (zona intrinseca) N = Na /(b2-1).
Campioni e disposizione dei contatti
Conviene operare con campioni di Ge (in forma di lamina parallelepipeda) perchè sul
Ge si possono saldare a stagno i contatti necessari.
Il campione di semiconduttore è posto entro una scatola di rame (cella di misura =
ambiente isotermo) che può essere inserita fra le espansioni polari di un magnete.
Sul campione sono saldati 7 fili nella configurazione mostrata in figura 2.
I contatti 1 e 2 (le cui tensioni sono misurabili alle boccole indicate con TP1 e TP2)
servono per misurare la d.d.p. V=RI ai capi del campione (tecnica di misura a quattro
fili) in modo da poter ottenere la resistenza elettrica R. (è necessario usare un
amplificatore con ingresso differenziale la cui uscita è riferita a massa e può quindi
essere letta da qualsiasi interfaccia).
4
Figura 2: Schema a blocchi
I contatti 3 e 4 (TP3 e TP4) servono a far passare la corrente prodotta dal circuito
generatore di corrente costante descritto in figura 3.
Figura 3: Schema del generatore di corrente costante e degli amplificatori differenziali
Il contatto 7 (TP5) è il punto di riferimento per la misura della d.d.p. di Hall ed i punti 5
e 6 sul lato opposto vanno ad un potenziometro P il cui cursore centrale (TP6) viene
usato per ottenere il bilanciamento della d.d.p. di Hall in assenza di campo magnetico.
Per minimizzare gli offset degli amplificatori OP07 si cortocircuitano gli ingressi e si
minimizzano le tensioni in uscita (VR VH) mediante i trimmer R28 e R38. Quindi, posto
5
il campione lontano dal campo magnetico, si minimizza l’uscita del canale VH
aggiustando il potenziometro “Balance” (Figura 3).
Inserendo il campione nel campo magnetico si può valutare (ed eventualmente
cambiare) il valore del guadagno di entrambi i canali di amplificazione, confrontando la
tensione VH con la d.d.p. tra TP5 e TP6.
Figura 4: Frontale della scatola di controllo
Il guadagno dei due canali (VR e VH) può essere variato agendo sia sulla resistenza che
controlla il guadagno del differenziale (INA114: G=1+50k/RG) e che può essere
dimezzata mediante i commutatori (jumpers) J1 e J3, sia agendo sui potenziometri R22
e R32, che controllano il guadagno del secondo stadio non invertente (OP07). Il
guadagno complessivo di ciascun canale può variare tra 4 e 135.
L’accesso ai vari potenziometri è consentito da fori nella lastra in plexiglass sul
coperchio della scatola di controllo (figura 5).
Figura 5: La scheda del circuito di controllo: l’accesso ai potenziometri è consentito da fori nella
protezione in plexiglass
La corrente è misurabile come caduta di tensione ai capi della resistenza Ri da 100 ohm:
Vi = I Ri. Questa è la tensione ad una estremità del campione, misurabile al test point
TP3. L’altra estremità si porta alla tensione Vo = -I Rx= -(Rx/Ri)Vi (misurabile al test
point TP4): essa deve restare (in modulo) minore della tensione di alimentazione (15V),
altrimenti l’operazionale AD841 satura e smette di regolare la corrente.
6
Il valore ottimale della corrente di polarizzazione è un compromesso tra la necessità di
generare segnali (VR e VH sono proporzionali a I) non troppo piccoli, e quella di non
eccedere nella dissipazione sul campione per effetto Joule (proporzionale a I2).
La necessità di usare una configurazione a 4 contatti per una corretta misura della
resistenza del campione può essere evidenziata misurando la caduta di potenziale tra i
contatti 3 e 4 (TP3 e TP4) (come si farebbe con un normale ohmetro che opera con soli
due contatti) e tra i contatti 1 e 2 (TP1 e TP2) (come si fa in questo apparato): si noterà
che il secondo valore è notevolmente inferiore al primo (nel quale la caduta di tensione
attraverso i contatti non è trascurabile, dato che i contatti 3 e 4 sono percorsi dalla
corrente di polarizzazione).Dato che la differenza di potenziale tra i contatti 1 e 2 è
misurata da un voltmetro ad alta impedenza (INA114) , la corrente attraverso i contatti è
trascurabile e di conseguenza anche la caduta di tensione attraverso di essi).
Misure di VH e di resistenza
In presenza di campo, ruotando il campione di 180 gradi (che equivale a invertire la
direzione di B) si deve trovare per VH un valore uguale in modulo ma di segno opposto.
Il valore del campo magnetico prodotto da due magneti permanenti montati su supporto
a “C” può essere variato cambiando la lunghezza del traferro (uno dei dischi
magnetizzati è su supporto scorrevole), e misurato mediante gaussmetro in funzione
della lunghezza del traferro (figura 6).
Figura 6: Il dispositivo a vite per variare la lunghezza del traferro
In mancanza di un gaussmetro si può usare la curva di calibrazione data in figura 6,
insieme al polinomio interpolante.
Si può verificare che la tensione di Hall VH è proporzionale a I e a B (figura 4), e
calcolare il coefficiente di Hall RH = VH t/ (I B) (t è lo spessore del campione) e da
questo la concentrazione dei portatori liberi.
7
Utilizzando l’interfaccia LabPro con software LoggerPro, si possono registrare coppie
di valori in modalità semi-automatica (“Events with entry Mode”): fissata la corrente I
nel campione, si può variare la distanza tra i magneti agendo sulla vite (e si legge il
valore di B con il gaussmetro) l’interfaccia acquisisce il valore di VH e chiede di
digitare il valore letto di B. Invece a valore fisso di B si può acquisire normalmente in
funzione del tempo la coppia di valori I e VH, mentre si agisce sul potenziometro R29
(prelevando con una sonda la tensione Vi alla boccola TP3 e registrandone il valore
diviso per 100 su una colonna calcolata e con una seconda sonda la tensione VH e
registrandone il valore diviso per il guadagno in una seconda colonna calcolata) .
Piccole deviazioni dalla linearità che si possono osservare per i valori più elevati della
corrente di polarizzazione possono essere dovute all'autoriscaldamento del campione ed
al fatto che RH diminuisce rapidamente al crescere della temperatura. Deviazioni dalla
linearità a valori di campo magnetico elevato sono invece spiegabili derivando una
approssimazione al secondo ordine di RH (Appendice 1) .
Figura 7: Tensione di Hall in funzione di I (B=4.5 kGauss), e di B (I=3 mA).
L'acquisizione dati, a corrente e campo magnetico costanti, al variare della temperatura
può essere fatta usando un canale per leggere la d.d.p. ai capi del campione, un secondo
per leggere la d.d.p. di Hall ed il terzo per leggere la tensione della termocoppia,
La temperatura della cella di misura deve essere variata lentamente nel tempo in modo
da poter registrare i valori di VH e di V=RI in condizioni di quasi equilibrio.
Inizialmente la si raffredda immergendo in un dewar di azoto liquido il gambo di
alluminio avvitato sotto la cella di misura. Raggiunta la temperatura di circa -120 oC si
toglie l'azoto liquido residuo e si eseguono misure campionate mentre la temperatura
cresce.
Quando la temperatura del campione si avvicina alla temperatura ambiente si comincia
a scaldare facendo passare corrente nella resistenza elettrica avvolta attorno alla base in
alluminio della cella di misura.
8
La corrente di riscaldamento va fatta crescere lentamente, fino ad un massimo di circa
200 gradi centigradi, mediante il circuito di controllo (figura 8). Tutta l’escursione
termica richiede un tempo dell'ordine di un’ora.
E’ opportuno iniziare a scaldare ad erogando una piccola corrente al riscaldatore
(potenziometro di controllo ruotato tutto in senso antiorario), per evitare che
l’accensione del riscaldatore possa disturbare l’amplificatore contenuto nel sensore a
termocoppia: un LED rosso, posto sulla scatola fissata al giogo che porta i magneti, in
tal caso si accende, e si deve spegnere il riscaldatore e riaccenderlo con piccola
corrente. Il LED si accende anche in caso si interrompa la giunzione di termocoppia.
Figura 8: Regolatore di corrente del riscaldatore
La temperatura si misura mediante una termocoppia Fe-Costantana (tipo J, standard
americano) amplificata mediante l'integrato AD594. Questo è un amplificatore dotato
anche di circuito di compensazione delle variazioni di temperatura ambiente (in
sostituzione della giunzione fredda in ghiaccio fondente) che dà in uscita una tensione
all'incirca proporzionale alla temperatura centigrada con costante di proporzionalità di
≈10 mV/oC
La curva di risposta di AD594 è presentata in figura 9 insieme al polinomio di 5 grado
che meglio la interpola.
Figura 9: taratura AD594 con polinomio del V ordine
9
Risultati tipici
Il campione utilizzato ha uno spessore t= 0.5 mm , larghezza w= 10mm e lunghezza l=
15mm.
Un esempio dell'andamento della d.d.p. di Hall e della resistenza, in un campione
polarizzato con corrente di 3 mA ed immerso in un campo di 0.42T, è riportato in figura
10. (La resistenza è calcolata tenendo conto che il guadagno del canale VR è stato
settato al valore Gr=20).
Figura 10: VH e R in funzione della temperatura
In figura 11 è riportato l’andamento del parametro RH in funzione di T, ricavato dai dati
di figura 10.
Figura 11: RH in funzione della temperatura
Il logaritmo della resistenza in funzione di 1/2kT (ove k=8.617x10-5 eV/K è la costante
di Boltzmann) è riportato in figura 12.
Dalla pendenza di questo grafico nella zona intrinseca si ricava il valore dell'ampiezza
della banda proibita (energy gap) estrapolato linearmente a T=0 K, da confrontare con il
valore noto per il Ge (Ego = 0.78 eV, cfr. Appendice 2).
10
Figura 12: log(R) vs. 1/2kT
Appendice 1: RH nel caso di cristalli poco drogati e campi magnetici elevati
L’equazione del moto dei portatori di carica (F=ma) si può scrivere:
" dv v %
! !
m$ + ' = qE + qv ( B
# dt ! &
ove la carica q vale ±e per lacune o elettroni e si tiene conto del tempo medio tra due
collisioni (τ) e della forza di Lorentz.
In condizioni stazionarie l’accelerazione è nulla e di conseguenza per le componenti di
velocità lungo l’asse x (direzione della corrente Ix e campo di spazzolamento Ex) si ha
rispettivamente per elettroni e lacune (B è diretto lungo l’asse z):
e"
e" ! !
v e x = ! Ex ! v # B = !µ e Ex ! µ ev e yB
m
m
v hx = µ h Ex + µ hv h x B
(A1)
dove µ=eτ/m è la mobilità (con indice e per elettroni e h per lacune), e per le
componenti lungo l’asse y si hanno analoghe relazioni:
ve y = !µ e Ey ! µ eve x B
(A2)
vh y = µ h E y + µ h vh x B
La densità di corrente lungo x (Jx = e vhxp –evexn ) può quindi essere scritta:
(
)
J x ! e( pµ h + nµ e ) Ex + e pµ hv hy " nµ e vey B !
(
)
! e( pµ h + nµ e )E x + e pµ 2h " nµ 2e BE y
(A3)
dove abbiamo approssimato le velocità nella direzione y solo come vy≈ µyEy ,
trascurando qui cioè la componente dovuta alla forza di Lorentz.
Tenendo conto che Ey<<Ex, per piccoli valori del campo magnetico B la (A3) è
approssimabile come:
J x ! e( pµ h + nµ e ) E x
(A4)
11
In condizioni di densità di corrente trascurabile lungo y (impedenza elevata dello
strumento che legge la tensione di Hall Vy) vale la relazione :
J y = epvh y ! enve y = 0
che, introducendo le definizioni delle velocità vhx e vex , diventa:
J y = ep µ h E y + µ h vh x B ! en(!µ e Ey ! µ ev e x B) = 0
(
(
)
)
e( pµh + nµe )E y + e pµ h vh x + nµ ev ex B = 0
Qui, esplicitando Ey si ottiene:
Ey = B
( pµ v
h hx
+ nµ ev e x
( pµ h + nµ e )
)
(A5)
Questa relazione si semplifica, nell’ipotesi che si possano ancora approssimare le
velocità solo come vx≈ µxEx (cioè trascurando la correzione di Lorentz per piccoli valori
del campo magnetico B) in:
Ey
( pµ
!B
2
h
" nµ 2e )
( pµ h + nµ e )
(A6)
Ex
e il coefficiente di Hall RH risulta allora essere:
Ey
pµ 2h ! nµ 2e
RH = !
"
J x Bz e ( pµ h + nµ e ) 2
(A7)
L’espressione (A7) vale solo per piccoli valori di B.
Altrimenti si deve tener conto di termini del secondo ordine, ad esempio introducendo
la dipendenza da B della densità di corrente lungo x, utilizzando nella (A7) la
definizione (A3) per Jx invece che la (A4).
In tal caso il coefficiente di Hall, diventa dipendente dal valore di B , e tende a saturare
a valori elevati :
2&
#
#
2
2
&
2
2
pµ
"
nµ
E y % pµh " nµe
%
(
h
e
(
RH (B) =
! %B
E x ( / Be %( pµ h + nµe ) + B 2
( Ex =
BJ x %$ ( pµ h + nµ e ) ('
pµh + nµe ) (
(
%
$
'
(
=
( pµ
e ( pµ h + nµ e )
2
2
h
)
" nµ2e
)
(
2&
#
pµ 2h " nµ2e (
%
2
%1+ B
2(
%
(
pµ
+
nµ
(
)
h
e
$
'
(
)
=
)
RH (B = 0)
1 + kB 2
12
Appendice 2: Andamento di Eg con la temperatura
L’ampiezza della banda proibita dipende dalla temperatura, e per il germanio i dati
sperimentali in letteratura sono bene interpolati dalla seguente funzione:
Eg (T)= 0.742- 4.8·10-4·T2/(T+235) (eV)
Questa funzione può essere approssimata, nella regione di alte temperature, da una
relazione lineare del tipo Eg (T)= A+BT, ove la costante A è il valore di Eg estrapolato
linearmente a T=0: Eg0 = A = 0.78 eV
Dato che nella zona intrinseca (alte temperature) in un semiconduttore drogato la
resistenza dipende dalla temperatura come exp{+Eg/(2kT)}, il grafico di ln(R) vs. 1/2kT
è una retta di pendenza Eg0
Cenni storici
Edwin Herbert Hall scoprì quello che poi venne chiamato “effetto Hall” nel 1879 mentre
lavorava alla sua tesi di dottorato in fisica. Il dottor Hall cercava di capire se la resistenza
elettrica di una bobina fosse influenzata dalla presenza di un magnete. Dopo mille
tentativi e fallimenti alla fine scoprì che il campo magnetico modifica le linee
equipotenziali in un conduttore che trasporta corrente. Questo effetto corrisponde alla
tensione (VH) perpendicolare alla direzione della corrente elettrica nel conduttore.
I sensori di campo magnetico ad effetto Hall
L’effetto Hall rimase una curiosità di laboratorio fino a metà del secolo scorso, dato il
piccolo valore di RH per i materiali fino ad allora conosciuti. Con l’avvento della
13
tecnologia dei semiconduttori (in particolare dei composti III-V) divenne facile misurare
tensioni di Hall con valori molti ordini di grandezza superiori rispetto ai valori ottenibili
con i metalli, e comparvero così i primi sensori magnetici ad effetto Hall.
I materiali più usati a questo scopo sono stati antimoniuro di indio (InSb), arseniuro di
indio (InAs) e arseniuro di gallio (GaAs). I sensori GaAs hanno grande sensibilità ma
anche elevato rumore. I sensori InSb hanno grande sensibilità, basso rumore ma
coefficiente termico dell’ordine 1%/°C. I sensori InAs hanno sensibilità inferiore ma
piccolo coefficiente termico e basso rumore. Per questo motivo la maggior parte dei
moderni sensori Hall sono fatti di InAs.
Precauzioni
L’uso di campi magnetici elevati, come quelli prodotti dai potenti magneti permanenti
in dotazione richiede qualche precauzione. Si deve evitare di avvicinare troppo ai
magneti qualsiasi oggetto magnetizzabile (orologi, cellulari, cacciaviti…), pena la
magnetizzazione permanente dell’oggetto in questione.
Evitare di svitare completamente la ghiera di regolazione del traferro: quando i due
magneti permanenti vengono a contatto risulta difficile staccarli, data la grande forza
con cui essi si attraggono.
Riferimenti bibliografici
C.L.Chin e C.R.Westgate, The Hall Effect and Its Applications, Plenum Press, NY, 1979
http://www.ioffe.rssi.ru/SVA/NSM/Semicond/Ge/reference.html
A. C Melissinos , J. Napolitano, Experiments in Modern Physics, Academic Press, 2003
14