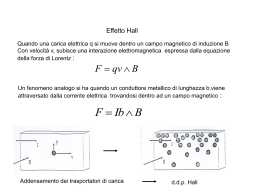
Misure di trasporto elettronico (Effetto Hall)
Modello semplice:
a
Data un barretta a x b x l =  x l, nella quale
scorre una densità di corrente
b
i= j
l
ortogonale a un campo magnetico B, sui
portatori agisce la forza di Lorentz
F = e vd x B
esistendo quindi un campo elettromotore
EH= vd x B = j/ne x B
EH= jB/ne
essendo j = nevd
Si accumulano, quindi, cariche sulle due facce con normale ortogonali a j e B
creando un contro-campo elettrostatico Eel che cresce finché Eel = EH .
1
Eel genera una d.d.p. E H = Eel b che può essere misurata.
Il segno del campo e della E H dipendono dal segno dei portatori che si accumulano
sulla faccia superiore della barretta (dato il verso di B)
E H = Eel b = j B /ne b = i B b/(n e  ) = i B /(n e a)
Da cui si possono ricavare segno e concentrazione, n, dei portatori
n = i B /(e a E H )
2
La densità di corrente
j = i /  = n e vd = n e EL = n e VL /l
dalla quale si può ricavare la mobilità,  , avendo già ricavato n
 = i l /( n e  VL)
Si individua il coefficiente Hall RH = 1/en
E’ anche da tener presente il fattore di proporzionalità tra E H e B
 = E H/B = i /n e a
da cui la misura di B tramite misura di E a i costante (sonda Hall)
3
Una descrizione più accurata è più complessa (Bloch – Boltzmann)
Si deve tener conto:
a) della struttura a bande del solido, per calcolare la velocità media di portatori e
la funzione di distribuzione.
b) del tempo medio di scattering .
c) della frequenza di ciclotrone C , e
del tipo di traiettoria dei portatori
d) . . .
Il coefficiente Hall assume una forma complessa.
Nell’ipotesi, solitamente utilizzata, B molto elevato, C  >> 1, RH assume la
forma semplice
RH = 1/ne
4
Metodi di misura della resistività e dell’effetto Hall
La resistenza di un campione si misura velocemente con il metodo volt-
amperometrico (R = V/I ); ma per resistenze molto piccole la resistenza di
contatto tra puntali e campione è paragonabile se non maggiore a quella del
campione stesso.
Quindi si usano quattro punte: due per misurare (o iniettare) la corrente e due tra le
quali misurare la V
Due geometrie: quattro punte in linea e van der Pauw
Il primo preferito per campioni sottili e monocristalli, il secondo per film
strutturati, campioni irregolari, ceramici
5
Quattro punte (in linea)
Campione di forma rettangolare (parallelepipedo) con diversi contatti per le varie
misure.
Si possono misurare  e VH
La resistività si calcola a partire da
ove VO e I sono la d.d.p. longitudinale e la corrente che scorre ;
l è la
distanza tra i contatti di tensione/resistenza e S la sezione trasversale del
campione .
6
Per misurare VH (d.d.p. trasversale dovuta alla presenza di B) potrebbero bastare
due contatti ortogonali a B e I. Ma così facendo si misura anche la differenza di
resistenza dovuta al disallineamento dei contatti opposti, anche senza B
Allora si usano due contatti dalla stessa parte, con un potenziometro (R variabile)
tra di loro. Così si azzera la d.d.p. trasversale in assenza di B.
Il potenziometro deve avere una resistenza molto maggiore di quella del
campione, così da non assorbire corrente, ma senza introdurre ulteriore rumore!
Questo metodo è noto come “delle cinque punte”!
7
Svantaggi:
- Devono essere note con grande precisione la dimensioni del campione che
deve essere molto regolare;
- il flusso di corrente deve essere omogeneo in tutto il campione ( campioni
lunghi e stretti, circa 4 volte)
- le dimensioni dei contatti dovrebbero essere trascurabili rispetto alle
dimensione del campione.
Tutto ciò non rende questo metodo adatto a piccoli cristalli di forma irregolare.
8
van der Pauw
Cinque condizioni per poter usare questa geometria
1) Campione piatto e di spessore uniforme, d
2) senza buchi isolati
3) omogeneo e isotropo
4) tutte e quattro i contatti devono essere ai bordi del campione
5) l’area di ogni contatto dovrebbe essere almeno un ordine di grandezza
inferiore all’area del campione
9
la relazione tra resistività  e V/I è:
ove R1 = V1/I1 e V1 è la d.d.p. tra C e D quando tra A e B
C
B
D
A
scorre la corrente I1. mentre R2 = V2/I2 con V2 la d.d.p. tra
C e B quando tra A e D scorre la corrente I2.
f è un fattore geometrico che dipende dal rapporto R1 / R2
In caso di perfetta simmetria dei contatti R1 = R2 e f = 1
Il coefficiente di Hall si può ottenere come
ove I è la corrente tra A e C e VH è la differenza tra la d.d.p. VBD con il campo
magnetico e senza.
10
Tuttavia può capitare, nella realtà, che VBD ,anche senza B, sia molto maggiore di
VH a causa del disallineamento dei contatti.
Anche piccoli drift in temperatura possono portare a variazioni di resistenza
comparabili con il segnale Hall .
A questo si può porre rimedio rifacendo la misura con B invertito e mediando.
Oppure scambiando i contatti di corrente con quelli di d.d.p.
. ..
Rumore elettrico e pratiche sperimentali
Il segnale Hall è tipicamente dell’ordine dei nV, quindi può essere paragonabile o
anche inferiore al rumore elettrico. E’,quindi, importante utilizzare tecniche
sperimentali per ottimizzare il rapporto segnale/rumore.
11
Tipici contributi al rumore, sono: 1) rumore bianco (ampio range di frequenze)
raccolto dai contatti o dai fili; 2) tensione d.c. dovuta al potenziale di contatto tra
fili e campione, o anche a minime differenza di temperatura.
Metodo principale per superare questi effetti è l’uso della modulazione del segnale
e della sua misura con un amplificatore agganciato in fase (lock-in).
In pratica:
1) Check del segnale a.c. : deve essere proporzionale alla corrente e indipendente
dalla frequenza.
2) Nel caso di v.d.P, si misurano R1 e R2 per determinare il fattore geometrico f
3) Si porta a zero la d.d.p. senza B, con il potenziometro
4) A ogni valore del campo B, si mediano i due valori ottenuti invertendo il campo
12
Sonda Hall per la misura di B (sia esterno che prodotto dal campione)
Per misurare la magnetizzazione di un campione
Doppia croce, una col campione e una vuota per sottrarre il contributi del
campo magnetico esterno
13
Strumentazione
2 criostati con T < 1 K ed elevati campi magnetici
Generatori di segnale ed amplificatore lock-in
14
15