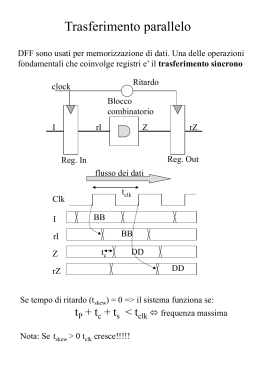
Chapter 1
Circuiti sequenziali:
macchine a stati
Nella prima parte del corso ci siamo occupati dei circuiti combinatori. In un circuito combinatorio con un ouput Z funzione degli input
X1 ; : : : Xn , Z varia istantaneamente in risposta a cambiamenti degli
input. Diciamo che e un circuito senza memoria.
In un circuito sequenziale avente input X1 ; : : : Xn e ouput Z , Z
non varia istantaneamente in risposta a cambiamenti degli input. Le
caratteristiche di un tale circuito sono:
Presenza di un segnale di clock di input (onda quadra periodica).
All'interno del circuito e presente una memoria contenente un
certo numero di bit di informazione. Il contenuto di questa memoria e detto lo stato del circuito. I bit della memoria, vale a dire
lo stato, possono cambiare a seconda dei valori dei segnali input,
solo in corrispondenza del fronte di salita del segnale di clock.
I segnali di output sono combinazioni logiche dei bit della memo-
ria di stato (macchina a stati di Moore). In questo modo anche i
segnali di output possono variare solo in corrispondenza del fronte
di salita del segnale di clock.
Consideriamo alcuni esempi:
1
2
CHAPTER 1.
CIRCUITI SEQUENZIALI: MACCHINE A STATI
Figure 1.1: Diagramma temporale di un contatore a 3 bit.
Figure 1.2: Diagramma degli stati di un contatore a 3 bit free-running.
3
Contatore a 3 bit free-running Questo contatore non ha input
oltre al clock.
In questo caso il conteggio e uguale allo stato (e coerente col fatto
che gli output debbano essere combinazioni logiche dei bit di stato).
Fig. 1.1 mostra il diagramma temporale. Vediamo che lo stato cambia solo in corrispondenza dei fronti di salita del clock. Non essendoci
input, lo stato cambia su ogni fronte. Consideriamo ad esempio il ciclo di clock in cui lo stato e 3 (stato corrente). Lo stato successivo e
zero. Vediamo che il valore dello stato successivo dipende dallo stato
corrente.
Possiamo visualizzare il comportamento temporale del contatore con
un diagramma a bolle (Fig. 1.2). Questo diagramma e una rappresentazione astratta del comportamento del circuito, non una rappresentazione circuitale. A ciascuno stato, oltre al codice numerico, viene
assegnato anche un nome simbolico. Ogni bolla rappresenta un possibile stato, mentre le frecce connettono ciascuno stato ai possibili stati
successivi e deniscono quindi le transizioni da uno stato al successivo.
Nel caso presente, per ciascuno stato esiste un solo stato successivo.
Contatore a 2 bit con segnale di enable Questo contatore ha
un input denominato enable oltre al clock.
Anche in questo caso il conteggio e uguale allo stato.
Fig. 1.3 mostra il diagramma temporale. Lo stato cambia sempre in
corrispondenza dei fronti di salita del clock ma solo quando il segnale di
enable e 1. Quindi in questo caso lo stato successivo dipende sia dallo
stato corrente che dal valore del segnale di input.
Il segnale enable mostrato in gura e un tipico segnale sincrono. La
sua fase e ssata rispetto al segnale di clock: il segnale cambia sempre
leggermente dopo il fronte di salita di clk. Il contatore campiona il
segnale di enable su ogni fronte di salita di clk e cambia lo stato nel
fronte in cui vede enable=1, come indicato in gura. E' essenziale tenere
conto di questo aspetto per comprendere a fondo il comportamento di
questi circuiti.
Fig. 1.4 mostra il diagramma degli stati del contatore con enable.
Alle frecce delle transizioni sono associate ora i valori logici del segnale
di input che determina le transizioni. Partiamo dallo stato iniziale S0.
La transizione a S1 avviene solo se enable=1. Se enable=0 lo stato
non cambia e questo corrisponde alla freccia che inizia e termina nel
4
CHAPTER 1.
CIRCUITI SEQUENZIALI: MACCHINE A STATI
Figure 1.3: Diagramma temporale di un contatore a 2 bit con enable.
Figure 1.4: Diagramma degli stati di un contatore a 2 bit con enable.
5
Figure 1.5: Diagramma temporale di un contatore a 2 bit con output
Cout.
medesimo stato. Un comportamento simile si ha per gli altri stati.
Contatore a 3 bit con segnale di output Cout Il contatore pu
o
produrre, oltre al conteggio, anche un segnale di output quando il conteggio raggiunge il valore massimo. In Fig. 1.5 e mostrato il diagramma
temporale per questo caso per un contatore a 2 bit. Anche Cout e, per
costruzione, un segnale sincrono col clock. In questo esempio, esso e
inoltre interamente funzione dei bit di stato e non degli eventuali input come l'enable. Nel seguito considereremo solo macchine a stati di
questo tipo (macchine a stati di Moore).
La logica di eccitazione Come passo successivo, a partire dal
diagramma degli stati possiamo elaborare una tavola della vertia che
visualizza per ciascuno stato corrente e segnali di input lo stato successivo. Fig. 1.6 mostra questa tavola per il contatore con enable a due
bit. I bit dello stato successivo sono denotati aggiungendo il simbolo *.
Nella tavola appaiono anche gli eventuali segnali di output come Cout.
6
CHAPTER 1.
CIRCUITI SEQUENZIALI: MACCHINE A STATI
Figure 1.6: Tavola per la logica di eccitazione del contatore a 2 bit con
enable e segnale di output Cout.
Possiamo considerare questa tavola come una tavola della verita vera
e propria descrivente una funzione logica - detta logica di eccitazione avente come input Q1, Q0, enable e come output Q1*, Q0* e Cout.
La memoria di stato: Flip Flop D. Entriamo adesso dentro
la memoria. Ciascun bit della memoria e conservato in un dispositivo
detto Flip Flop di tipo D. Il simbolo di circuito e mostrato in Fig. 1.7.
Questo circuito campiona il valore sull'input D su ogni fronte di salita
del segnale di clock e lo passa all'output Q. Fig. 1.8 mostra un diagramma temporale in cui e mostrato Q per un certo pattern di D. Il
valore di Q non puo cambiare fra un fronte di salita e il successivo viene mantenuto congelato. Questo e mostrato nella gura Fig. 1.8 in
basso, in cui D ha diverse variazioni fra due fronti di salite del segnale
di clock. Queste variazioni vengono ignorate dal FF.
Dentro il contatore a 2 bit free-running Nel caso del contatore
a 2 bit la memoria di stato e formata da due FF. Resta in problema
di denire gli input D0 e D1 dei due FF. Torniamo alla logica di eccitazione. Le equazioni logiche per Q0* e Q1* sono
0 =
Q1 =
Q
0
Q 0 Q1
Q
0
(1.1)
(1.2)
7
Figure 1.7: Simbolo e funzionamento del FF D.
Figure 1.8: Funzionamento del FF D: diagrammi temporali.
8
CHAPTER 1.
CIRCUITI SEQUENZIALI: MACCHINE A STATI
Figure 1.9: il contatore a 2 bit free running completo e diagrammi
temporali.
Q0* e Q1* sono lo stato successivo a Q0 e Q1. Se quindi vengono
mandati in input ai due FF, sul fronte di salita di clock successivo
verranno campionati dai FF e passati agli output Q0 e Q1, cioe, diventeranno i nuovi stati correnti. In questo modo si ha la transizione
corretta da uno stato corrente allo stato successivo (si veda anche il
diagramma temporale di Fig. 1.9). La Fig. 1.9 mostra il circuito completo corrispondente al contatore. I bit Q0 e Q1 saranno gli output
corrispondenti al conteggio.
Macchine a stati Il contatore e un esempio di macchina a stati.
Adesso generalizzeremo il discorso considerando qualche altro esempio.
Consideriamo un circuito che controlla le frecce di una macchina. Col
tasto SW0 si attiva la freccia sinistra (corrispondente al LED0 sulla
scheda), che comincia a lampeggiare con una frequenza di circa 1 Hz.
Schiacciando nuovamente SW0 la freccia viene disattivata.
9
Figure 1.10: Macchina a stati per far lampeggiare un led premendo il
tasto SW0.
Il controllo della freccia destra avviene con SW1 in modo analogo
alla freccia sinistra.
Consideriamo una prima versione del circuito che controlla la sola
freccia sinistra. Un possbile diagramma degli stati e mostrato in Fig. 1.10.
Nell stato iniziale, denotato IDLE, il led e spento. Ci sono due frecce
che partono da IDLE. Se SW0=1 lo stato diventa LED0-ON. Se SW0=0
lo stato resta IDLE. Una volta passati nello stato LED0-ON c'e' una
sola freccia senza condizione: questo signica che si passa automaticamente allo stato LED0-OFF. Il circuito resta nello stato LED0-ON per
un solo ciclo di clock. Nello stato LED0-ON viene generato il segnale
LED0 che accende il led della scheda. Una volta in LED0-OFF si passa
nuovamente in LED0-ON e cos via. In questo modo si cicla all'innito
fra LED0-ON e LED0-OFF.
In questo circuito, una volta attivato il lampeggiamento, non c'e
10 CHAPTER
1.
CIRCUITI SEQUENZIALI: MACCHINE A STATI
Figure 1.11: Macchina a stati per il controllo della freccia sinistra.
modo di arrestarlo. Il diagramma di Fig. 1.11 risolve questo problema. Questa volta dallo stato LED0-ON partono due freccie corrispondenti a due possibili stati successivi: LED0-OFF se SW=0 e IDLE se
SW0=1 (tasto premuto nuovamente). Lo stesso si ha per LED0-OFF:
se SW0=0 si va in LED0-ON altrimenti in IDLE. Fig. 1.11 mostra la
tavola delle transizioni degli stati (assegnando IDLE Q1Q0=00, LED0ON Q1Q0=01, LED0-OFF Q1Q0=10).
Questo esempio e utile per illustrare un altro aspetto importante.
Lo stato LED0-ON ha due possibili stati successivi raggiunti da due
freccie diverse corrispondenti a due diverse condizioni (una SW0=0,
l'altra SW0=1). Non ci possono essere due freccie con due condizioni
per i segnali di input uguali, oppure due frecce senza condizione (transizione automatica). In questo caso il circuito non saprebbe decidere
quale sarebbe lo stato successivo e il comportamento in pratica diventa
impredicibile. In particolare, l'AND logico delle condizioni di tutte le
11
Figure 1.12: Circuito corrispondente alla macchina a stati per il controllo della freccia sinistra.
possibili coppie di frecce che lasciano uno stato deve essere zero: questo
e soddisfatto per LED0-ON poiche SW0*SW0'=0. L'OR logico delle
condizioni associate a tutte le freccie che lasciano uno stato deve essere
uno: anche in questo caso cio e soddisfatto poiche SW0+SW0'=0.
Le equazioni della logica di eccitazione sono
0 =
Q1 =
Q
1 Q0 S W 0 + Q1 Q 0 S W 0
Q1 Q 0 S W 0 :
Q
0
0
0
0
0
0
Il circuito completo e mostrato in Fig. 1.12. Il diagramma temporale
che illustra il funzionamento del circuito e mostrato in Fig. 1.13.
12 CHAPTER
1.
CIRCUITI SEQUENZIALI: MACCHINE A STATI
Figure 1.13: Diagramma temporale della macchina a stati per la freccia
sinistra.