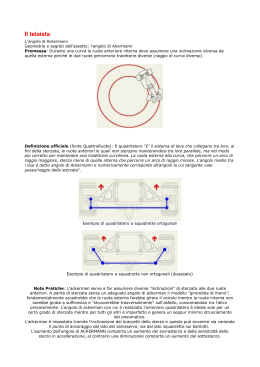
19/05/2011
Università degli Studi di Firenze
Facoltà di Ingegneria
Corso di Meccanica del Veicolo
Anno Accademico 2010/2011
Moto Uniforme in Curva del Motociclo
Ing. Andrea Rindi – Ing. Alessandro Ridolfi
13/05/2011
1 di 61
Indice delle lezioni
Introduzione
Geometria del motociclo
• Grandezze principali
Pneumatici
• Forze scambiate fra pneumatico e strada (con particolare
attenzione alle forze laterali)
• Momenti scambiati fra pneumatico e strada
Moto uniforme in curva
• Comportamento direzionale
• Modelli del motociclo in curva
2 di 61
1
19/05/2011
Introduzione
La cinematica di un veicolo a due ruote è piuttosto complessa rispetto a quella
di un veicolo a quattro ruote. Si tenga presente che un motociclo (veicolo su due
ruote) è per sua natura instabile e che la sua dinamica è fortemente influenzata
dallo stile di guida del pilota.
Lo studio della cinematica e della dinamica di un motociclo dipende dal livello di
approssimazione del modello utilizzato. Gli elementi critici da modellare sono
soprattutto quelli cedevoli (ad esempio, pneumatici e sospensioni).
Un modello fortemente semplificato che considera il motociclo composto da soli
4 elementi rigidi (avantreno, ruota anteriore, retrotreno e ruota posteriore) e
dotato di sospensioni rigide ha comunque almeno 7 gradi di libertà.
3 di 61
Geometria del motociclo – grandezze principali
Passo, p: distanza tra i punti di contatto dei pneumatici con il piano stradale. Varia
tra 1200 mm per uno scooter a 1600 mm per moto turistiche.
Angolo di inclinazione dello sterzo, : angolo compreso fra l’asse verticale e l’asse
di rotazione dello sterzo (asse di sterzo). Valori tipici sono da 19° a 32°.
Avancorsa, a: distanza tra il punto di contatto della ruota anteriore ed il punto di
intersezione dell’asse di sterzo con il piano stradale. Varia da 75 mm a 120 mm.
4 di 61
2
19/05/2011
Geometria del motociclo – grandezze principali
Avanzamento (o offset), d: distanza tra l’asse di sterzo ed il centro della ruota
anteriore. Il centro ruota è tipicamente avanzato rispetto all’asse di sterzo: valori
tipici sono da 25 mm a 40 mm.
La combinazione dei valori dell’avanzamento d e dell’angolo si sterzo determinano il valore desiderato di avancorsa a.
5 di 61
Geometria del motociclo – grandezze principali
Avancorsa normale, : distanza tra il punto di contatto della ruota anteriore con il
suolo e l’asse di sterzo. L’angolo di inclinazione dello sterzo lega il valore
dell’avancorsa a quello dell’avancorsa normale:
Le forze laterali anteriori generano momenti attorno all’asse di sterzo proporzionali
al valore di avancorsa normale .
6 di 61
3
19/05/2011
Geometria del motociclo – grandezze principali
Un aumento del passo determina:
• Maggior difficoltà nell’effettuare curve di raggio ridotto.
• Aumento della coppia di sterzo nell’inserimento del veicolo in curva.
• Aumento della stabilità in rettilineo legato alla diminuzione dei trasferimenti di
carico fra anteriore e posteriore: è più difficile impennare in fase di
accelerazione o sollevare il retrotreno in frenata.
In sintesi, si ha un comportamento del motociclo migliore in rettilineo e
peggiore in curva. Si ha maggior stabilità, ma minor maneggevolezza.
Un aumento dell’avancorsa (ottenuto ad esempio con un aumento dell’angolo di
sterzo, con un minor offset o con un pneumatico di raggio maggiore) determina:
• Aumento della stabilità del veicolo in rettilineo (il valore dell’avancorsa, come
vedremo, è molto importante per la stabilità del motociclo).
• Peggioramento di manovrabilità e maneggevolezza.
In sintesi, come per il passo, si ha un comportamento del motociclo migliore in
rettilineo e peggiore in curva. Si ha maggior stabilità, ma minor
maneggevolezza.
7 di 61
Geometria del motociclo – grandezze principali
L’ avancorsa a è positiva se il punto di intersezione dell’asse di sterzo con il piano stradale C
è avanzato rispetto al punto di contatto della ruota anteriore con il suolo P.
Consideriamo un motociclo, con avancorsa positiva, che avanza su strada piana e rettilinea
con velocità V. Ipotizziamo che tale veicolo sia sottoposto ad una perturbazione esterna
che ruota il manubrio verso sinistra (come in figura); il vettore velocità V può esser
scomposto nelle due componenti:
• di rotolamento;
• laterale (ortogonale al piano della ruota).
8 di 61
4
19/05/2011
Geometria del motociclo – grandezze principali
La forza di attrito laterale F che si genera ha la stessa direzione di ma verso opposto. Nasce un momento, pari a , che tende a riportare lo sterzo
nella posizione di equilibrio (ruota non sterzata).
Un’avancorsa positiva ha dunque un effetto raddrizzante e stabilizzante; durante
la marcia del motociclo consente di ‘’assorbire’’ gli effetti di disturbo che si possono
generare sull’avantreno dovuti, ad esempio, a buche o a colpi di vento.
9 di 61
Geometria del motociclo – grandezze principali
Viceversa se l’avancorsa è negativa (punto P avanzato rispetto a C) si ha l’effetto
contrario: effetto destabilizzante , ovvero si genera un momento che tende ad
accentuare il disturbo.
La definizione di avancorsa implica che essa possa passare da positiva (fig.1) a
negativa (fig.2) durante la marcia; nel superamento di elevate asperità stradali (ad
esempio gradini o rallentatori) l’avancorsa può diventare negativa.
10 di 61
5
19/05/2011
Geometria del motociclo – grandezze principali
Posizione longitudinale del baricentro, b: misurata a partire dal punto di contatto
della ruota posteriore con il suolo.
Posizione verticale del baricentro, h: misurata a partire dal piano stradale.
NOTA: la presenza del pilota è tale da far arretrare il baricentro complessivo del
sistema motociclo + pilota.
11 di 61
Geometria del motociclo – grandezze principali
Baricentro alto:
• Maggior trasferimento di carico fra anteriore e posteriore.
• Facilità di impennamento sulla ruota anteriore in frenata; facilità di impennamento
sulla ruota posteriore in accelerazione.
Baricentro basso:
• Limitato trasferimento di carico fra anteriore e posteriore.
• Possibilità di slittamento (perdita di aderenza) della ruota posteriore in accelerazione;
possibilità di slittamento della ruota anteriore in frenata.
Baricentro avanzato (/ 0.5):
• Maggior carico gravante sulla ruota anteriore.
• Possibilità di slittamento della ruota posteriore in accelerazione.
• Maggior facilità di impennamento sulla ruota anteriore in frenata.
• Il motociclo può assumere (a seconda delle caratteristiche degli pneumatici) un
comportamento maggiormente sovrasterzante.
Baricentro arretrato (/ # 0.5):
• Maggior carico gravante sulla ruota posteriore.
• Più facile scaricare a terra la potenza in accelerazione.
• Maggior facilità di impennamento sulla ruota posteriore in accelerazione.
• Il motociclo può assumere (a seconda delle caratteristiche degli pneumatici) un
comportamento maggiormente sottosterzante.
12 di 61
6
19/05/2011
Geometria del motociclo – grandezze principali
L’angolo di rollio, $ è definito come l’angolo, misurato sul piano YZ, che
si forma tra il piano meridiano della ruota posteriore ed il piano verticale.
Quando il manubrio è ruotato di
un angolo di sterzata pari a %il
rollio del retrotreno $ è diverso
dal rollio dell’avantreno &. Con
angolo di sterzata non nullo,
l’inclinazione (l’angolo di rollio)
dell’avantreno
è
sempre
maggiore rispetto al retrotreno
(& $).
Equazione linearizzata:
& $ ' %sin
13 di 61
Geometria del motociclo – grandezze principali
Angolo di sterzata effettivo
Angolo di sterzata, %: ampiezza dell’angolo compreso tra il piano meridiano della
ruota posteriore e quello della ruota anteriore (‘’angolo di sterzo al manubrio’’).
Angolo di sterzata effettivo, ∆: intersezione di tale angolo con il piano stradale
(‘’angolo di sterzo a terra’’).
14 di 61
7
19/05/2011
Pneumatici - forze e momenti
Lo pneumatico (elemento deformabile) è uno dei componenti più importanti di un
motociclo: le prestazioni di un motociclo e le sensazioni di guida del pilota sono
fortemente influenzate dalle caratteristiche degli pneumatici. Si tenga infatti
presente che il controllo del moto del veicolo avviene grazie alla generazione di forze
longitudinali e laterali, scambiate fra lo pneumatico e il piano stradale.
Gli pneumatici devono assicurare:
• Comfort: lo pneumatico è in pratica il primo elemento del sistema sospensivo.
• Aderenza: per trasferire correttamente al suolo le forze di spinta, di frenata e le
forze laterali.
15 di 61
Pneumatici - forze e momenti
Le forze ed i momenti agenti sullo pneumatico sono:
•
•
•
•
•
•
Forza longitudinale (,- ): positiva se di spinta, negativa se di frenata.
Forza laterale (,. ): ortogonale alla forza longitudinale.
Forza verticale (,/ o 0): carico gravante, ortogonale al piano stradale.
Momento di rollio (1- ): momento agente secondo l’asse x.
Momento resistente al rotolamento (1. ): momento agente secondo l’asse y.
Momento di imbardata (1/ ): momento agente secondo l’asse z.
16 di 61
8
19/05/2011
Pneumatici - forze e momenti
Angolo di rollio, $: angolo, misurato sul piano YZ, che si forma tra il piano meridiano della
ruota e il piano verticale.
Angolo di deriva, 2: angolo, misurato sul piano stradale, che si forma tra la direzione
effettiva del moto (velocità V) e l’intersezione della ruota con il piano stradale.
Durante una curva, la forza laterale ,. agisce sul pneumatico. Tale forza può esser
suddivisa in due contributi distinti ,.3 e ,.4 , dipendenti rispettivamente dall’angolo di
rollio $ e dall’angolo di deriva 2:
,. ,.3 ' ,.4
17 di 61
Pneumatici - forze e momenti
Si consideri uno pneumatico inclinato di un certo angolo di rollio che avanza con angolo di
deriva nullo. Nel caso di pneumatico deformabile si ha un’orma di contatto ed il punto P
abbandona la traiettoria ellittica teorica (proiezione sul piano stradale che si avrebbe nel
caso di ruota indeformata) per seguirne una rettilinea nella direzione di avanzamento della
ruota. La deformazione della carcassa PP” avviene per effetto dello schiacciamento (PP’) e
per la deformazione dovuta alla forza laterale generata dall’angolo di rollio ,.3 (P’P”).
,.3 è importante soprattutto per piccoli angoli di deriva.
18 di 61
9
19/05/2011
Pneumatici - forze e momenti
Si consideri uno pneumatico che rotola e che striscia lateralmente (angolo di deriva non
nullo); in questo caso l’orma di contatto risulta distorta.
Nel tratto AB (aderenza) i punti descrivono una traiettoria rettilinea con velocità con
direzione parallela alla velocità di avanzamento V. Nel tratto BC (slittamento) le tensioni
di richiamo elastico sono maggiori delle forze di aderenza e quindi i punti deviano in
senso opposto strisciando fino all’uscita dall’area di contatto.
La forza laterale generata dall’angolo di deriva ,.4 è data dall’integrale delle tensioni
laterali. La zona di slittamento aumenta all’aumentare dell’angolo di deriva 2.
19 di 61
Pneumatici - forze e momenti
Si definisce coefficiente di aderenza laterale il rapporto tra la forza laterale ed
il carico normale agenti sul pneumatico:
56 6
7
Per angoli di deriva
piccoli l’andamento è
approssimativamente
lineare.
Il coefficiente di attrito laterale definito come il rapporto tra la forza laterale
massima ed il carico normale può raggiungere valori fra 1.2 e 1.5 in caso di
superficie stradale pulita ed asciutta.
20 di 61
10
19/05/2011
Pneumatici - forze e momenti
Rigidezza di deriva, kλ (10÷30 rad-1)
Rigidezza di rollio, k$ (0.7÷1.2 rad-1)
kλ =
kϕ =
1 dFy
Fz d λ
λ = 0,ϕ = 0
1 dFy
Fz d ϕ
λ = 0,ϕ = 0
21 di 61
Pneumatici - forze e momenti
In condizioni statiche, fissati gli angoli di deriva e di rollio, e per piccole variazioni degli stessi,
la forza laterale 6 è solitamente espressa in funzione della rigidezza di deriva 89 e della
rigidezza di rollio 8: , secondo la seguente espressione lineare:
6 69 ' 6: 89 2 ' 8: $ 7 ;9 2 ' ;: $
In cui
;9 89 7 e ;: 8: 7
sono rispettivamente le rigidezze di deriva e di rollio dimensionali [N/rad].
22 di 61
11
19/05/2011
Pneumatici - forze e momenti
Si consideri un motociclo in curva in moto
stazionario (raggio di curvatura costante,
velocità costante e per ipotesi angolo di
sterzata nullo). Per l’equilibrio dei momenti si
ha che la forza laterale normalizzata è pari alla
tangente dell’angolo di rollio:
6
tg$
7
La forza laterale ,. è la forza necessaria per
garantire l’equilibrio in curva.
Gli pneumatici di tipo motociclistico sono caratterizzati da una forza laterale ,. che è
solitamente generata, fino a determinati angoli di rollio, quasi solo dalla componente di rollio
,.3 . Questa componente si manifesta più velocemente rispetto alla componente dovuta alla
deriva ,.4 , poiché dipende dalla deformazione della carcassa del pneumatico, mentre la
componente di deriva è legata all’angolo di deriva che richiede maggior tempo per essere
raggiunto.
23 di 61
Pneumatici - forze e momenti
A destra: spinta laterale normalizzata dovuta al solo rollio (linea continua) e forza laterale
normalizzata necessaria per l’equilibrio in curva (linea a tratto).
Se $ < 28° la forza laterale richiesta ,. < forza dovuta al rollio ,.3 . Poiché la forza laterale
generata deve essere uguale a quella necessaria per l’equilibrio in curva, la diminuzione di
forza laterale si ha grazie ad una deriva negativa 2 # 0 (contributo opposto di ,.4 ).
Se $ > 28° la forza laterale richiesta ,. > forza dovuta al rollio ,.3 . Poiché la forza laterale
generata deve essere uguale a quella necessaria per l’equilibrio in curva, l’aumento di forza
laterale si ha grazie ad una deriva positiva 2 0 (contributo concorde di ,.4 ).
24 di 61
12
19/05/2011
Pneumatici - forze e momenti
Altro tipo di pneumatico in cui la spinta di rollio ,.3 è sempre inferiore alla forza
laterale ,. necessaria per l’equilibrio in curva.
In tal caso, poiché la forza laterale generata deve essere uguale a quella necessaria
per l’equilibrio in curva, servirà sempre una deriva positiva 2 0.
25 di 61
Pneumatici - forze e momenti
Le forze laterali, la loro generazione e la loro dipendenza dall’angolo di rollio sono di
fondamentale importanza per la definizione del comportamento direzionale del
motociclo (sottosterzante, sovrasterzante o neutro). Tale argomento sarà trattato più in
dettaglio nel seguito, ma si ritiene utile fare già alcune osservazioni considerando la
condizione di equilibrio in curva:
• Se la forza laterale necessaria all’anteriore richiede un angolo di deriva maggiore di
quello necessario al posteriore, all’aumentare dell’angolo di rollio il motociclo tenderà
ad avere un comportamento sottosterzante (maggiori slittamenti dell’anteriore).
• Viceversa se la forza laterale necessaria al posteriore richiede un angolo di deriva
maggiore di quello necessario all’anteriore, all’aumentare dell’angolo di rollio il
motociclo tenderà ad avere un comportamento sovrasterzante (maggiori slittamenti
del posteriore).
• Il comportamento neutro, come noto, si ha quando i due angoli di deriva sono uguali.
• Poiché il comportamento ideale (condizioni di sterzatura cinematica) si ottiene quando
gli angoli di deriva sono nulli, si capisce allora che tale condizione può esser raggiunta
quando la forza laterale necessaria per l’equilibrio è prodotta dal solo rollio.
26 di 61
13
19/05/2011
Pneumatici - forze e momenti
Momento di autoallineamento
Analogamente al caso dell’autoveicolo,
le tensioni tangenziali non hanno una
distribuzione simmetrica; la forza
laterale di deriva risultante è posta a
distanza t (braccio a terra o avancorsa
dello
pneumatico)
dal
centro
dell’orma di contatto.
Si genera dunque il momento di
autoallineamento, pari al prodotto della
forza laterale di deriva per l’avancorsa del
pneumatico 69 >. Tale momento tende a
ruotare la ruota in modo da ridurre
l’angolo di deriva.
NOTA: l’avancorsa dello pneumatico t (parametro tipico del pneumatico) NON deve
essere confusa con l’avancorsa a (parametro geometrico del veicolo).
27 di 61
Pneumatici - forze e momenti
Momento di torsione
C0: intersezione dell’asse di rotazione della ruota con il piano stradale
C : centro della curva
r: raggio della ruota
R: raggio di curvatura
28 di 61
14
19/05/2011
Pneumatici - forze e momenti
Momento di torsione
Se per ipotesi C0≡C le velocità periferiche pei punti A e B sarebbero uguali alle velocità di
avanzamento dovute alla rotazione della ruota:
?@ Ω@
?A ΩA
Se invece C0 è all’interno C e nel punto medio dell’impronta la velocità periferica è uguale alla
velocità di avanzamento si ha:
?@ ' ?A
Ω @ ' A
2
2
All’interno: velocità di avanzamento > velocità periferica ⇒ scorrimento negativo (come per
una ruota frenata) verso l’interno della curva.
All’esterno: velocità periferica > velocità di avanzamento ⇒ scorrimento positivo (come per
una ruota in trazione) verso l’esterno della curva.
Si ha quindi tensione di compressione nella zona esterna e di trazione nella zona interna ⇒
momento di torsione che tende a far percorrere alla ruota una traiettoria con raggio di
curvatura minore (effetto sovrasterzante).
Il momento torcente è approssimativamente proporzionale all’angolo di rollio.
29 di 61
Pneumatici - forze e momenti
Abbiamo visto dunque che sullo pneumatico agiscono due momenti di segno
opposto: il momento di autoallineamento ed il momento di torsione.
La loro somma definisce il momento di imbardata del pneumatico, il cui andamento
qualitativo al variare dell’angolo di deriva è mostrato nella figura sottostante. Valori
positivi del momento di imbardata corrispondono ad un effetto disallineante.
30 di 61
15
19/05/2011
Pneumatici - forze e momenti
Momento di spinta/frenata
Il braccio di azione della forza longitudinale D dipende dalla deformazione laterale dello
pneumatico E e dallo spostamento laterale del punto di contatto del pneumatico .
La forza di spinta genera un momento che tende ad allineare il piano dello pneumatico
nella direzione della velocità, mentre la forza frenante genera un momento di senso
opposto, disallineante.
31 di 61
Moto uniforme in curva
Si vuole studiare il comportamento di un motociclo in curva in condizioni di moto
uniforme: il motociclo percorre una curva con raggio di curvatura costante a
velocità costante (condizioni stazionarie). Per semplicità non si considerano
dunque le ‘‘fasi transitorie’’ di ingresso ed uscita curva.
A differenza di un autoveicolo, durante una traiettoria curva il motociclo è inclinato
(rollio) verso l’interno della curva. Anche lo sterzo è ruotato dalla stessa parte.
32 di 61
16
19/05/2011
Moto uniforme in curva
Un motociclo, nel moto uniforme in curva in curva, può presentare un comportamento:
• Neutro: per garantire l’equilibrio del motociclo in curva il pilota deve esercitare una coppia
al manubrio nulla.
• Sovrasterzante: per garantire l’equilibrio del motociclo in curva il pilota deve esercitare una
coppia al manubrio negativa, cioè discorde con la rotazione dello sterzo.
• Sottosterzante: per garantire l’equilibrio del motociclo in curva il pilota deve esercitare una
coppia al manubrio positiva, cioè concorde con la rotazione dello sterzo.
Queste caratteristiche concorrono a definire la sensazione di guidabilità del motociclo.
Il comportamento direzionale del motociclo è strettamente legato alle caratteristiche degli
pneumatici.
33 di 61
Moto uniforme in curva
Ipotesi semplificative:
- Curva a raggio costante ;
- Velocità del motociclo costante V;
- Effetto giroscopico trascurabile;
- Angolo di sterzata nullo;
- Ruote lenticolari.
Le reazioni a terra devono equilibrare la
forza peso (verticale) e la forza
centrifuga (orizzontale).
Dall’equilibrio dei momenti in curva si può ricavare l’angolo di rollio ideale $ :
tg$ 6
ΩI
I
⇒ $ arctg
arctg
7
g
g
in cui Ωè la velocità angolare di percorrenza della curva; la velocità di avanzamento del
motociclo è Ω .
34 di 61
17
19/05/2011
Moto uniforme in curva
In realtà le ruote non sono lenticolari, ma hanno uno spessore pari a 2>. L’angolo di rollio
effettivo $ (per avere il baricentro G nella medesima posizione) è maggiore di quello ideale
$ , $ $ ' Δ$, e l’incremento Δ$ può essere calcolato da semplici considerazioni
geometriche:
sin∆$
sin$
>
KL M >N
35 di 61
Moto uniforme in curva
L’angolo di rollio effettivo $ è allora pari a:
I
>sin arctg
I
g
$ arctg
' arcsin
g
LM>
Per calcolare ∆$ è dunque sufficiente conoscere la velocità di avanzamento del motociclo
ed il raggio di curvatura, oltre all’altezza del baricentro e lo spessore dei pneumatici.
La relazione precedente evidenzia inoltre che ∆$ cresce sia all’aumentare dell’angolo di
rollio ideale che del raggio dei toroidi, sia al diminuire dell’altezza del baricentro.
A parità di curvatura della traiettoria e di velocità angolare di imbardata, l’adozione di
pneumatici di larghezza maggiorata costringe il pilota ad eseguire manovre con angoli di
rollio maggiori. A parità di sezione di pneumatici, per percorrere la stessa curva con la
medesima velocità di avanzamento, una motocicletta con il baricentro basso deve essere
inclinata di più rispetto ad una motocicletta con baricentro più alto.
Nella realtà occorre tenere conto del fatto che, in generale, in curva l’angolo di sterzata
non è nullo, per cui la formula può esser valida solo in prima approssimazione.
36 di 61
18
19/05/2011
Moto uniforme in curva
Nella realtà l’angolo di rollio è influenzato anche dalla posizione del
pilota sulla sella:
a) Pilota immobile sulla sella ⇒ il
baricentro rimane nel piano del
motoveicolo ⇒ l’angolo di rollio è
quello calcolato.
b) Pilota verso l’esterno ⇒ il baricentro
si sposta verso l’esterno della curva ⇒
si deve inclinare di più il motoveicolo.
c) Pilota verso interno ⇒ il baricentro si
sposta verso l’interno della curva ⇒ si
deve inclinare di meno il motoveicolo.
Nelle competizioni il pilota sposta il
proprio corpo verso l’interno della
curva in modo da ridurre il rollio del
motociclo e controllarlo meglio.
NOTA: considerando il livello di aderenza laterale disponibile con pneumatici di tipo
standard, il massimo angolo di rollio possibile è pari a circa 45° .
37 di 61
Moto uniforme in curva
Studio del comportamento direzionale del motociclo
Si consideri il moto uniforme in curva di un motociclo; se le ruote fossero in condizioni
di puro rotolamento, il vettore velocità V sarebbe contenuto nel piano delle ruote
(angolo di deriva 2 nullo). Solo quando → 0 (forza centrifuga assai limitata) gli angoli
di deriva possono essere trascurati. Si parla allora di condizioni di sterzatura cinematica.
Per generare le forze laterali di reazione in curva è necessario uno strisciamento laterale
del pneumatico rispetto al terreno (anche se, come visto, nasce una forza laterale anche
per effetto del rollio). Lo strisciamento è fisicamente collegato alla presenza di un
angolo di deriva 2 diverso da zero; in generale gli angoli di deriva non sono nulli e si
parla in questo caso di condizioni di sterzatura dinamica.
38 di 61
19
19/05/2011
Moto uniforme in curva
Studio del comportamento direzionale del motociclo
COMPORTAMENTO NEUTRO (2 2 )
Se 2 2 0 (condizioni di sterzatura
cinematica) il centro di rotazione (QR ) è
dato dall’intersezione delle rette ortogonali
ai piani delle ruote nei punti di contatto
con il suolo.
Se 2 2 (anche S 0) il motociclo ha
comportamento neutro: il centro di
rotazione (Q) si sposta, verso l’avantreno,
su una circonferenza passante per QR e per
i punti di contatto delle ruote con il suolo
(circonferenza dei centri di istantanea
rotazione neutri).
L’angolo di sterzata effettivo ∆ rimane invariato al variare di 2 2 S 0 (il raggio di
curvatura rimane approssimativamente costante).
39 di 61
Moto uniforme in curva
Studio del comportamento direzionale del motociclo
COMPORTAMENTO SOTTOSTERZANTE (2 2 )
Il centro di rotazione (Q) si sposta all’esterno della circonferenza dei centri neutri ed il
raggio di curvatura effettivo è maggiore di quello ideale R (relativo alle condizioni
di sterzatura cinematica). Il motociclo tende quindi ad ‘‘aprire’’ la curva impostata.
40 di 61
20
19/05/2011
Moto uniforme in curva
Studio del comportamento direzionale del motociclo
COMPORTAMENTO SOVRASTERZANTE (2 # 2 )
Il centro di rotazione (Q) si sposta all’interno della circonferenza dei centri neutri ed il
raggio di curvatura effettivo è minore di quello ideale R (relativo alle condizioni di
sterzatura cinematica). Il motociclo tende quindi a ‘‘chiudere’’ la curva impostata.
41 di 61
Moto uniforme in curva
Dunque, come per un autoveicolo, il comportamento direzionale del motociclo (la sua
guidabilità) è fortemente legato ai valori degli angoli di deriva anteriore e posteriore (2 e
2 dipendono dalle caratteristiche degli pneumatici montati).
NOTA: a differenza di un autoveicolo, è preferibile avere un comportamento del
motociclo leggermente sovrasterzante, piuttosto che sottosterzante.
Con un motociclo con comportamento sottosterzante il pilota (per correggere la curva) è
costretto ad aumentare l’angolo di sterzata; se il manubrio è molto ruotato, la forza
laterale reattiva richiesta può esser maggiore di quella resa disponibile dall’aderenza tra
pneumatico anteriore e strada, con il conseguente scivolamento della ruota anteriore
(caduta del pilota). Un comportamento sottosterzante è quindi maggiormente pericoloso
in quanto il pilota non ha modo di controllare il veicolo dopo la perdita di aderenza
dell’anteriore.
Con un motociclo con comportamento sovrasterzante, invece, il pilota, anche se la ruota
posteriore scivola poiché la forza laterale reattiva richiesta è maggiore di quella resa
disponibile dall’aderenza tra pneumatico posteriore e strada, con una manovra di
controsterzo ha maggior probabilità di ripristinare le condizioni di equilibrio in curva
(evitando così la caduta).
42 di 61
21
19/05/2011
Moto uniforme in curva
MODELLO SEMPLIFICATO
Si trascurano i piccoli spostamenti dei punti di contatto degli pneumatici.
Il raggio di curvatura della ruota posteriore T , in funzione degli angoli di deriva e
dell’angolo di sterzata, è pari a:
T tg ∆ M 2 cos 2 ' sin2
43 di 61
Moto uniforme in curva
MODELLO SEMPLIFICATO
Le equazioni di equilibrio scritte rispetto al sistema di riferimento QVWX sono:
Forze lungo X
Y M sinΔ ' Z[\ ΩI M @ 0
Forze lungo Y
cosΔ ' Z]\ ΩI ' 0
Forze lungo Z
Zg M ^ M ^ 0
Momenti intorno ad X
M_67 ΩI M ^ ' ^ ] ' Zg]\ ' _` ' _` Ωcos$ 0
Momenti intorno ad Y
_a7 ΩI ' ^ ' [ M Zg[\ M @ b\ ' ^ [ 0
Momenti intorno a Z
' [ cosΔ ' ] sinΔ ' [ M Y] ' @ ]\ 0
Tali equazioni di equilibrio e l’equazione con la quale si determina il raggio di
curvatura della ruota posteriore T costituiscono un sistema non lineare.
44 di 61
22
19/05/2011
Moto uniforme in curva
MODELLO SEMPLIFICATO
Il significato dei simboli è il seguente:
S spinta necessaria per mantenere il moto uniforme in curva;
@ forza di resistenza aerodinamica (supposta applicata nel baricentro G);
, forze laterali esercitate dalla strada sui pneumatici;
^ , ^ forze verticali esercitate dalla strada sui pneumatici;
_` , _` momenti d’inerzia delle ruote;
, velocità angolari delle ruote;
_a7 , _67 ‘’momenti d’inerzia centrifugo-composti’’ del motociclo rispetto alla terna QVWX ;
[\ , ]\ , b\ coordinate del baricentro G nel sistema di riferimento QVWX ;
[ , ] coordinate del punto di contatto della ruota posteriore nel sistema QVWX ;
Ω velocità di imbardata;
Δ angolo di sterzata cinematico (misurato sul piano stradale).
45 di 61
Moto uniforme in curva
MODELLO SEMPLIFICATO
Raggio di curvatura adimensionalizzato rispetto al raggio di curvatura teorico R .
Ipotesi: 8: 8: 0.8
• Veicolo sovrasterzante quando 89 89
• Veicolo neutro quando 89 89
• Veicolo sottosterzante quando 89 # 89
L’angolo di deriva dello
pneumatico è tanto maggiore
quanto minore è la sua
rigidezza di deriva.
46 di 61
23
19/05/2011
Moto uniforme in curva
MODELLO LINEARIZZATO
Rispetto al modello semplificato, si trascuri la dipendenza dell’orientazione della forza
centrifuga dagli angoli di deriva. Si ipotizzi inoltre che la curva sia caratterizzata da una
raggio di curvatura molto maggiore rispetto al passo del motociclo (vale alloraT ≫ ).
Si possono così ottenere con facilità le espressioni dei carichi verticali, delle forze laterali e
degli angoli di deriva:
CARICHI VERTICALI (ANTERIORE E POSTERIORE)
L
M
L
^ Zf M @ cos$^ Zf
' @ cos$
indicando con @ la forza di resistenza aerodinamica longitudinale (ipotizzando, per
semplicità, che essa sia applicata in corrispondenza del baricentro del sistema).
FORZE LATERALI (ANTERIORE E POSTERIORE)
T
M
ZΩI
ZΩI
T
cosΔ
la ruota anteriore è sterzata.
47 di 61
Moto uniforme in curva
MODELLO LINEARIZZATO
ANGOLI DI DERIVA (ANTERIORE E POSTERIORE):
Ricordandosi l’espressione linearizzata della forza laterale in funzione degli angoli di deriva e
di rollio, 6 89 2 ' 8: $ ^ , si ha:
ZΩI T
8:
1 2 M 8: $ M
$'
L
89 ^
89
Zf M @ cos$ 89 cosΔ
8:
1 2 M 8: $ M
$'
89 ^
89
M
T
M
L
Zf
' @ cos$ 89
ZΩI
Gli angoli di deriva dipendono da 2 contributi di segno opposto:
1. (-) dipendente dalla rigidezza di rollio. Se la rigidezza di rollio aumenta diminuisce l’angolo
di deriva (può anche diventare negativo).
2. (+) dipende da forza centrifuga (numeratore) e carico verticale (denominatore).
48 di 61
24
19/05/2011
Moto uniforme in curva
MODELLO LINEARIZZATO
Mantenendo le ipotesi precedenti (T ≫ , angoli di rollio, di deriva e di sterzata limitati),
si ipotizzi inoltre che il trasferimento di carico dovuto al contributo della forza
aerodinamica sia trascurabile rispetto ai carichi verticali gravanti sulle ruote.
M
^ ≅ Zf ^ ≅ Zf
Con tali ipotesi il rapporto fra le forze laterali e quelle verticali è uguale per la ruota
anteriore e per quella posteriore e pari alla tangente dell’angolo di rollio $:
T
I
I
T
I
ΩI
h
tg$
ΩI
tg$
^
gcosΔ gT cosΔ gT
^
g
gT
Gli angoli di deriva diventano allora pari a:
2 tg$ M 8: $
tg$ M 8: $
2 89
89
Si può notare dunque come gli angoli di deriva siano inversamente proporzionali alle
corrispondenti rigidezze di deriva e come dipendano dalla rigidezza di rollio e dell’angolo
di rollio $ (quindi dalla velocità di avanzamento del motociclo e dal raggio di curvatura).
49 di 61
Moto uniforme in curva
MODELLO LINEARIZZATO
Se la tangente dell’angolo di rollio risulta minore del prodotto8: $ l’angolo di deriva
diventa negativo.
Assumendo che tg$ h $, risulta:
2 M2 ijklm
knm
M
ijklo
kno
$
La differenza fra gli angoli di deriva anteriore e posteriore sintetizza il comportamento
direzionale del motociclo.
• Veicolo sovrasterzante quando 2 M 2 # 0
• Veicolo neutro quando2 M2 0
• Veicolo sottosterzante quando2 M2 0
NOTA: nel grafico 89 89 .
50 di 61
25
19/05/2011
Moto uniforme in curva
MODELLO LINEARIZZATO – velocità critica
Considerando il motociclo in curva con raggio di curvatura elevatoT ≫ ed angoli di deriva e
di sterzata piccoli (ipotesi realistiche), il raggio di curvatura della ruota posteriore T è pari a:
T Δ M 2 ' 2
Definiamo il parametro di sterzata p come il rapporto tra il raggio di curvatura effettivo del
veicolo ed il raggio di curvatura del veicolo in condizioni di sterzatura cinematica:
p
T T Δ
TR
Considerando le espressioni degli angoli di deriva, il parametro di sterzata può essere espresso
come:
I 1 M 8: 1 M 8:
p 1'
M
g
89
89
Se la velocità V aumenta il motociclo tende ad amplificare il proprio comportamento
direzionale.
51 di 61
Moto uniforme in curva
MODELLO LINEARIZZATO – velocità critica
Se le rigidezze di deriva sono molto elevate gli angoli di deriva tendono a zero e si ha un
motociclo con comportamento neutro, o più precisamente si possono raggiungere le
condizioni di sterzatura cinematica (tale condizione può esser raggiunta anche con velocità
V tendente a zero):
89 89 → ∞ ⇒ p 1
In presenza di angoli di deriva non nulli, ma uguali, il comportamento del motociclo è
neutro:
1 M 8: 1 M 8:
⇒ p 1
89
89
Si ha comportamento sottosterzante del motociclo quando:
1 M 8: 1 M 8:
⇒ p 1
89
89
Se il motociclo è sottosterzante il raggio di curvatura effettivo cresce all’aumentare della
velocità; sono quindi necessari angoli di sterzata via via maggiori per correggere la
traiettoria.
52 di 61
26
19/05/2011
Moto uniforme in curva
MODELLO LINEARIZZATO – velocità critica
Si ha invece comportamento sovrasterzante del motociclo quando:
1 M 8: 1 M 8:
#
⇒ p # 1
89
89
Se il motociclo è sovrasterzante il raggio di curvatura effettivo decresce all’aumentare della
velocità (il motociclo tende a chiudere la curva).
In questo caso p può annullarsi in corrispondenza di un determinato valore di velocità, detto
velocità critica; in tale condizione il raggio di curvatura effettivo tende a zero ed il motociclo
diviene incontrollabile.
La velocità critica è pari a:
g
⇒ p 0
1 M 8: 1 M 8:
M
89
89
53 di 61
Moto uniforme in curva
MODELLO LINEARIZZATO
Il comportamento direzionale del motociclo è legato alle caratteristiche degli pneumatici.
In base al modello linearizzato, considerando costanti le rigidezze di rollio e di deriva, sia
l’angolo di sterzata che la posizione longitudinale del baricentro non hanno alcuna influenza
sul comportamento direzionale. Nella realtà le rigidezze di rollio e di deriva sono
dipendenti dal carico: la rigidezza di rollio solitamente non varia molto con il carico (spesso
la si può assumere approssimativamente costante), mentre la rigidezza di deriva varia in
maniera maggiormente apprezzabile.
In generale per gli pneumatici dei motocicli l’andamento della rigidezza di deriva con il
carico è decrescente (in alcuni casi con un breve tratto iniziale crescente). Considerando la
presenza di tale tratto crescente ed una moto leggera, un avanzamento della posizione del
baricentro rende il motociclo leggermente sovrasterzante, viceversa un arretramento lo
rende sottosterzante.
NOTA: con ipotesi diverse sull’andamento delle rigidezze di rollio e di deriva in funzione del
carico (basate sull’acquisizione di dati sperimentali) variano le conclusioni appena esposte.
54 di 61
27
19/05/2011
Moto uniforme in curva
MODELLO COMPLESSO
Si considerano tutte le forze aerodinamiche ed i momenti aerodinamici agenti sul
motociclo; si considerano anche gli spostamenti dei punti di contatto delle ruote.
La risoluzione di tale modello consente di ricavare una serie di grafici significativi.
55 di 61
Moto uniforme in curva
MODELLO COMPLESSO
, → $, %
Un motociclo in curva a parità di velocità
di avanzamento V , di angolo di rollio $ e
di angolo di sterzata % percorre una
traiettoria la cui curvatura è dipendente
dai valori degli angoli di deriva dei
pneumatici (e quindi, come visto, dai
valori di rigidezza degli stessi).
Le condizioni di equilibrio di un
motociclo in moto uniforme in curva
sono rappresentate in termini di linee
iso-livello degli angoli % e $.
Comportamento neutro
56 di 61
28
19/05/2011
Moto uniforme in curva
MODELLO COMPLESSO
Comportamento sovrasterzante
Comportamento sottosterzante
57 di 61
Moto uniforme in curva
MODELLO COMPLESSO
Dai grafici mostrati si può notare che:
- per percorrere una curva a raggio costante, l’angolo di sterzata diminuisce
all’aumentare della velocità;
- con uno pneumatico anteriore con rigidezze maggiori (comportamento
sovrasterzante) l’angolo di sterzata necessario per l’equilibrio in curva, fissata una
certa velocità di percorrenza ed il raggio di curvatura, è minore; ad esempio, per
15Z/ e raggio di curvatura di 30Z l’angolo di sterzata è di circa 1° (mentre
nel caso di comportamento neutro è di circa 2°);
- con uno pneumatico posteriore con rigidezze maggiori (comportamento
sottosterzante) l’angolo di sterzata necessario per l’equilibrio in curva, fissata una
certa velocità di percorrenza ed il raggio di curvatura, è maggiore; ad esempio, per
15Z/ e raggio di curvatura di 30Z l’angolo di sterzata è di circa 3° (mentre
nel caso di comportamento neutro è di circa 2°).
58 di 61
29
19/05/2011
Moto uniforme in curva
Coppia di sterzo
Per garantire l’equilibrio in curva (moto uniforme), la coppia al manubrio resercitata
dal pilota deve essere opposta alla risultante dei 6 momenti generati dalle forze
agenti sull’avantreno (contributi allineanti e disallineanti).
r ' rE ' rT ' rs ' rt ' ru ' rv 0
59 di 61
Moto uniforme in curva
Coppia di sterzo
Dove:
rE contributo (+) della forza peso dell’avantreno
rT contributo (-) della forza centrifuga dell’avantreno
rs contributo (+) della forza reattiva verticale anteriore
rt contributo (-) della forza reattiva laterale anteriore
ru contributo (-) dell’effetto giroscopico dell’avantreno
rv contributo (+) del momento di torsione del
pneumatico anteriore.
Avendo indicato con (+) i contributi disallineanti
e con (-) quelli allineanti.
Il momento giroscopico
tende a far rollare il
motociclo dalla parte
opposta rispetto a quella
di sterzata.
60 di 61
30
19/05/2011
Riferimenti utili
Testi di riferimento:
• Vittore Cossalter, Motorcycle Dynamics (versione italiana), Edizioni
Progetto, 2008.
• Gaetano Cocco, Dinamica e tecnica della motocicletta, Giorgio
Nada Editore, 2001.
Alcuni siti utili:
• www.dinamoto.it
• www.ducati.com
• www.tonyfoale.com
61 di 61
31