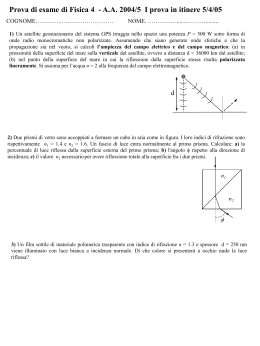
Prisma, dispersione della luce e misura dell’indice di
rifrazione
Premessa
Scopo dell’esperienza è la misura dell’indice di rifrazione del vetro con il quale è stato
costruito il prisma in dotazione. Si chiama prisma, in ottica, un oggetto trasparente che
abbia almeno due facce piane non parallele fra loro. Nel nostro caso si tratta di un prisma
geometrico retto a sezione triangolare.
In figura è mostrata una sezione (per noi) orizzontale del prisma in questione. Indichiamo
con α l’angolo al vertice del triangolo così ottenuto e seguiamo il percorso di un raggio
incidente dall’esterno su una faccia laterale del prisma.
Il raggio forma un angolo i con la normale
e viene in parte riflesso (circa il 4% in
energia) e prevalentemente rifratto.
L’angolo di rifrazione è r legato all’angolo
di incidenza dalla ben nota relazione
(legge di Snell):
sin i
=n
sin r
dove n indica l’indice di rifrazione del vetro
(da misurare) rispetto all’aria.
Il raggio attraversa il prisma e giunge sulla seconda faccia con un angolo s rispetto alla
normale. Di nuovo si verificano i fenomeni di riflessione e rifrazione. Se indichiamo con la
lettera e l’angolo con il quale il raggio fuoriesce dal prisma (angolo di emergenza), rispetto
alla normale alla faccia nel punto di uscita, possiamo ancora scrivere la relazione:
sin e
=n
sin s
che lega l’angolo s all’angolo e.
Il raggio emergente dal prisma risulta dunque deviato rispetto al raggio incidente di un
angolo che indichiamo con δ. Questo angolo di deviazione dipende dall’angolo di
incidenza, dall’angolo α e dall’indice di rifrazione del vetro.
Materiali
Per condurre l’esperimento disponi dei seguenti materiali:
•un prisma retto a base triangolare (il triangolo è equilatero, quindi α=60⁰);
•una base rotante munita di scala per la misura degli angoli sulla quale porre il prisma;
•una lente convergente;
•uno schermo;
•una sorgente luminosa (lampada);
•nastro adesivo opaco.
•banco ottico.
Pag. 1 di 3
lente convergente
lente convergente
Preparazione
Utilizzando il nastro adesivo prepara una fenditura verticale di fronte alla lampada posta
sul banco ottico. Posiziona la lente convergente sul banco di fronte alla fenditura,
allineandola con quest’ultima. La distanza tra lente e fenditura deve essere regolata in
modo tale da osservare un’immagine nitida della fenditura sullo schermo opaco posto a
distanza molto maggiore della focale della lente (come puoi stimare la focale della lente?).
Posiziona il supporto rotante con il prisma sul banco ottico di fronte alla lente convergente.
Ruota il supporto, come nella figura di sinistra, in modo tale che una faccia del prisma sia
perpendicolare al fascio di raggi in uscita dalla lente (che può essere considerato
praticamente un fascio parallelo).
Prendi nota dell’angolo indicato dalla scala sul supporto del prisma in questa posizione.
Se adesso ruoti il prisma delicatamente in senso orario e prendi nota del nuovo angolo
indicato sulla scala, la differenza tra questo angolo e quello di partenza è una misura
dell’angolo di incidenza sul prisma dei raggi uscenti dalla lente in questa nuova posizione,
come mostrato nella figura a destra. Puoi così variare e misurare l’angolo di incidenza dei
raggi sulla faccia del prisma tra zero e novanta gradi.
L’esperimento
Ruotando il prisma osserva l’immagine della fenditura sullo schermo. Cosa puoi
concludere? Il percorso di un raggio all’interno del prisma dipende dal “colore” (o meglio
dalla lunghezza d’onda della radiazione luminosa).
L’unica grandezza in gioco che può dipendere dal colore della luce incidente e può
dunque influenzare il percorso di ciascun colore è proprio l’indice di rifrazione del vetro (il
vetro viene detto per questo motivo un mezzo dispersivo ed il fenomeno osservato prende
il nome di dispersione della luce).
La deviazione di ciascun colore dipende dall’angolo di incidenza e dall’indice di rifrazione,
fissato l’angolo α del prisma. Questa dipendenza è piuttosto complicata, ma puoi notare,
ruotando il prisma, che per ciascun colore esiste un angolo di deviazione minima:
osservando lo schermo infatti e concentrandoti su un colore della striscia (che è composta
da tante immagini della fenditura affiancate, una per ciascun colore che compone la luce
bianca incidente) puoi notare che, ruotando il prisma con delicatezza, esiste una posizione
in cui il segmento della striscia di quel colore, che si sposta sullo schermo, sembra
fermarsi ed invertire il proprio movimento. Ferma il prisma nella posizione corrispondente
all’ “inversione” per quel dato colore che hai scelto.
Pag. 2 di 3
L’angolo di deviazione minima δm è l’angolo compreso tra la direzione del raggio incidente
e quella del raggio emergente (per quel colore) in questa posizione. Si dimostra che
l’angolo di deviazione minima si ha quando l’angolo d’incidenza e l’angolo di emergenza
sono uguali 1 . In questa posizione il legame tra le grandezze diventa più semplice e
consente di misurare l’indice di rifrazione del vetro (per quel dato colore) con una relazione
dove compare l’angolo α del prisma e l’angolo di incidenza (che puoi misurare sulla scala
del supporto del prisma come indicato in precedenza).
Facendo riferimento alla figura, con
semplici considerazioni geometriche e
sfruttando la legge di Snell per la
rifrazione, si ha:
sin em
=n
sin sm
ma nella posizione di minimo vale:
em = im
Inoltre:
rm = sm
e
rm + sm = α
Combinando le relazioni precedenti si giunge in definitiva alla relazione cercata:
n(λ) =
sin im
sin α/2
dove ricordo che nel nostro caso α=60⁰ e la lettera λ indica la dipendenza della misura
dalla lunghezza d’onda della radiazione (cioè dal colore).
Mettendoti nella posizione di deviazione minima per il colore scelto, misura l’indice di
rifrazione del vetro di cui è composto il prisma per quel colore.
Per finire, stima l’incertezza sulla misura dell’indice di rifrazione, indica le cause principali
di errore e gli accorgimenti utili per rendere la misura più precisa.
1
La dimostrazione può essere fatta per assurdo basandosi sull’unicità dell’angolo di deviazione minima
(puoi verificare sperimentalmente che al variare dell’angolo di incidenza tra zero e novanta gradi esiste una
sola posizione di minimo). Infatti se l’angolo di emergenza fosse diverso dall’angolo di incidenza invertendo
la propagazione della luce si otterrebbe una deviazione minima per un angolo di incidenza diverso, in
contraddizione con l’unicità del minimo.
Pag. 3 di 3