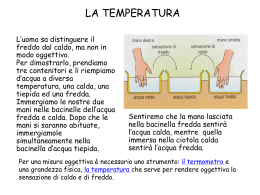
A.Celsius
W.T.Kelvin
TEMPERATURA E DILATAZIONE TERMICA
Lezione n.1 – classi SECONDE –Fisica
ITI «Torricelli» –S.Agata M.llo (ME)
Prof. Carmelo Peri
TEMPERATURA ED EQUILIBRIO TERMICO
TEMPERATURA E CALORE
•
La temperatura (T) è la misura dello stato termico di un corpo, cioè quanto sia caldo
o freddo
•
Il calore (Q) è l’energia che fluisce tra due corpi a causa della differenza delle loro
temperature ∆T
•
•
Lo strumento di misura della temperatura di un corpo è il Termometro
La realizzazione di un termometro è legata sia alla conoscenza del principio di
equilibrio termico che alla conoscenza del fenomeno chiamato dilatazione termica.
PRINCIPIO DI EQUILIBRIO TERMICO
•
Due corpi posti in contatto, dopo un certo periodo di tempo, raggiungono l’equilibrio
termico.
•
Due corpi sono in equilibrio termico se hanno la stessa temperatura.
DILATAZIONE TERMICA
•
Gli atomi di un corpo non sono fermi ma si muovono continuamente in prossimità ad una
posizione di equilibrio (vibrano). Un aumento di temperatura corrisponde ad un aumento
dell’energia posseduta dagli atomi che fa aumentare la loro distanza reciproca e
conseguentemente le dimensioni del corpo.
•
Un corpo si sviluppa secondo tre direzioni principali Lunghezza,
Larghezza, Altezza.
•
Si può notare che se aumentiamo la temperatura di un corpo
avente Lunghezza, larghezza e altezza dello stesso ordine di
grandezza gli allungamenti che subiscono queste tre grandezze
sono dello stesso ordine di grandezza e la dilatazione prende il
nome di DILATAZIONE TERMICA VOLUMICA
•
Mentre se aumentiamo la temperatura di un corpo in cui una delle tre grandezza è molto
piccola rispetto alle altre due (Lastra o piastra) le variazioni di questa grandezza è molto
piccola rispetto alle altre due che invece sono dello stesso ordine di grandezza e la
dilatazione prende il nome di DILATAZIONE TERMICA SUPERFICIALE
•
Infine se aumentiamo la temperatura di un corpo in cui una grandezza è molto grande
rispetto alle altre due (barra, tubo etc.) anche l’allungamento di questa grandezza sarà
molto grande rispetto alle altre due e la dilatazione prenderà il nome di DILATAZIONE
TERMICA LINEARE
DILATAZIONE TERMICA (LINEARE)

Esaminiamo un corpo che si sviluppi principalmente lungo Una direzione ad
esempio una sbarra o un tubo.


La lunghezza iniziale la indicheremo con L0
La temperatura iniziale la indicheremo con T0

Supponiamo di variare la temperatura portandola al valore T

La variazione di temperatura pari a ∆T=T- T0 determinerà una variazione di
lunghezza della sbarra pari a: ∆L=L- L0

Si può facilmente dimostrare che l’allungamento subito dalla sbarra è
direttamente proporzionale alla variazione di temperatura
∆L= a · L0 · ∆ T
L- L0 = a · L0 · (T- T0 )
α
è
il
coefficiente
di
dilatazione lineare
(un valore numerico che
dipende dal materiale)
Risolvendo rispetto ad L si ha:
L= L0 + a · L0 · ∆ T
e quindi:
L= L0 ·(1+ a · ∆ T)
DILATAZIONE TERMICA (SUPERFICIALE)






Esaminiamo un corpo che si sviluppi principalmente secondo due direzioni ad
esempio una lastra a base quadrata.
L’area di base sarà pari a A0 = L0 × L0 = L0 2
La temperatura iniziale è T0
Portiamo la temperatura del corpo alla temperatura T, conseguentemente le
dimensioni aumenteranno proporzionalmente alle lunghezze iniziali e saranno
rilevanti solo le variazioni relative alle lunghezze dei lati della base che saranno
pari a:
L= L0 ·(1+ a · ∆ T)
L’area di base sarà quindi pari a:
A = L2 = L0 2 ·(1+ a · ∆ T) 2 = L0 2 ·(1+ 2·a·∆ T+ a 2 ·∆ T 2 )
Essendo a un valore numerico molto piccolo il suo quadrato sarà ancora più
piccolo e pertanto il termine a 2 ·∆ T 2 può essere trascurato. Ne deriva che
A = A0 2 ·(1+2·a·∆ T) posto b=2·a si ha:
A = A0 ·(1+b·∆ T)
A-A0 =(1+b·∆ T)
∆ A =(1+b·∆ T)
b è il coefficiente di dilatazione superficiale
un valore numerico che dipende dal materiale pari al doppio del coefficiente
di dilatazione lineare
DILATAZIONE TERMICA (VOLUMICA)

Esaminiamo un corpo che si sviluppi similmente
lungo le tre direzioni ad esempio un cubo.

Ragionando in modo simile a quanto fatto in
precedenza ne deriva che
V = V0 2 ·(1+3·a·∆ T) posto g=3·a si ha:
V = V0 ·(1+g·∆ T)
V-V0 =(1+g·∆ T)
∆ V =(1+g·∆ T)
g è il coefficiente di dilatazione volumica
un valore numerico che dipende dal materiale pari al triplo del
coefficiente di dilatazione lineare
TEMPERATURA DI UN CORPO

Per assegnare un valore numerico alla T si sono utilizzate varie scale che sono
state individuate assegnando

- un valore arbitrario alla temperatura di fusione dell’acqua




TK =273.19 K
TC= 0 °C
TF= 32 °F
- Ed un valore arbitrario alla temperatura di ebollizione dell’acqua in condizione
di pressione atmosferica standard (a livello del mare)




Nella Scala Kelvin (SI) si è fissato
Nella Scala Celsius si è fissato
Nella Scala Fahrenheit si è fissato
Nella Scala Kelvin (SI) si è fissato
Nella Scala Celsius si è fissato
Nella Scala Fahrenheit si è fissato
TK =373.19 K
TC= 100 °C
TF= 212 °F
Formule di conversione
TC= TK -273
Tk= Tc +273
TC= 5·(TF -32)/9
TF= 9·(TC +32)/5
STRUMENTI DI MISURA DELLA TEMPERATURA
IL TERMOSCOPIO:

Un termoscopio è costituito da un tubo di vetro molto sottile che termina con un bulbo metallico
riempito da mercurio.
Mettendo a contatto il bulbo con un secondo corpo dopo un tempo sufficiente la posizione del
menisco del mercurio sarà rappresentativo della temperatura posseduta dal corpo (per il principio
di equilibrio termico e la legge di dilatazione termica). Con questo strumento è possibile
individuare la temperatura di un corpo solo qualitativamente e non quantitativamente.
IL TERMOMETRO

Un termometro è un termoscopio su cui è impressa una scala graduata.
L’operazione con cui si segna la scala graduata sul termoscopio prende il nome di Taratura del
termometro. Con questo strumento è possibile misurare la temperatura di un corpo.
TARATURA DEL TERMOMETRO

- Si dispone il termoscopio in una soluzione di acqua e ghiaccio, si aspetta che il livello del
mercurio si stabilizzi e si segna sul tubo di vetro con una tacca la temperatura indicandola
numericamente con 0°C (273,16 °K nella scala KELVIN).

Quindi si pone il termoscopio in corrispondenza dei vapori di acqua in ebollizione (alla pressione
standard) si segna la temperatura pari a 100°C (373,16 °K nella scala KELVIN).

- Si divide l’intervallo in 100 parti uguali.