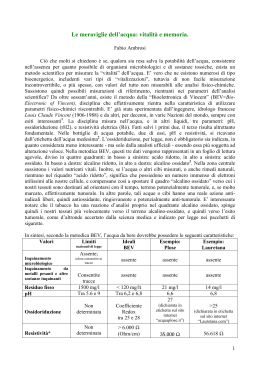
Le leggi di Ohm
Realizzazione a cura del Prof. Francesco Porfido
 La corrente elettrica (I) che scorre in un conduttore è direttamente
proporzionale alla differenza di potenziale elettrico (V) applicata alle sue
estremità A e B:
I
VA  VB
R
 Questa relazione è la legge di Ohm.
 La grandezza R, che è il rapporto fra la corrente
e la tensione, è chiamata resistenza del conduttore.
Georg Ohm (1789– 1854)
 La resistenza è l’ostacolo che gli elettroni incontrano durante il loro
percorso.
 L’inverso della resistenza è chiamata
conduttanza (G):
1
G
R
 In un grafico intensità/tensione la legge di Ohm
è rappresentata da una retta passante per
l’origine ed avente pendenza 1/R
Simboli circuitali della resistenza:
A
R
B
i
Legge di Ohm: VA VB  Ri
Ricorda ! …
V A  VB
i
R
La temperatura del conduttore è per ipotesi costante.
Vedremo più avanti in che modo essa influenzi il passaggio della corrente elettrica.
Tensione
Intensità
V/ i
Tensione
Intensità
V/ i
[volt]
[ampere]
[ohm]
[volt]
[ampere]
[ohm]
0,30
0,40
0,75
0,30
0,015
20
0,60
0,80
0,75
0,60
0,030
20
0,90
1,20
0,75
0,90
0,045
20
Conduttore
di rame
Conduttore
di
costantana
1.4
1.2
Maggiore pendenza
Legge di OHM
Minore resistenza
intensità di corrente [ampere]
1
0.8
rame
0.6
costantana
0.4
0.2
Minore pendenza
0
0
0.1
0.2
0.3
0.4
0.5
tensione [volt]
0.6
0.7
0.8
0.9
1
Maggiore resistenza
La resistenza o resistore è un elemento circuitale costituito da un materiale
che può essere attraversato da cariche elettriche.
Il suo valore R dipende dal materiale e dalle dimensioni.
La resistenza è legata alla resistività del materiale (ρ) dalla relazione:
R
dove:
l
A
A rappresenta la sezione trasversa
l la lunghezza del conduttore.
La resistenza si misura in ohm (Ω).
 OHMMETRO analogico e digitale: misura le resistenze.
In fisiologia (scienza che studia il funzionamento degli organismi viventi) si usa
frequentemente il concetto di conduttanza (G) che è l’inverso della resistenza.
L’unità di misura della conduttanza è il siemens (S).
Resistività di vari materiali:
Conduttori:
Rame, ferro, alluminio
Semiconduttori:
Germanio, silicio, boro
Isolanti:
Vetro, plastica, polistirolo
 = 10- 8  m
 = da 10- 3 a 10 2  m
 = 10+15  m
La densità di corrente J in un materiale è proporzionale al
E Unità di misura nel
campo elettrico E applicato. La costante di proporzionalità ρ  
sistema SI: ohm
j per metro = Ω m
è chiamata resistività.
Un materiale conduttore obbedisce alla legge di Ohm quando la resistività del
materiale è indipendente dall’intensità e direzione del campo elettrico applicato.
I
I
Si parla di conduttori lineari oppure
ohmici quando la curva caratteristica I -V è
una retta (metalli, vedi a destra), e di
conduttori non lineari oppure non ohmici
quando tale curva non è una retta (vedi a
ohmico
V
destra il grafico per un semiconduttore).
non ohmico
V
La resistività, in generale, dipende dalla temperatura.

Nei metalli essa varia linearmente (entro un limitato
intervallo di T) con la temperatura secondo la legge:
   0 1   T  T 0 
dove α è il coefficiente termico
della resistività,
T0 è una temperatura di riferimento
(spesso 20 °C) e ρ0 è la resistività a
questa temperatura
Cu
300
800
T(K)
I metalli obbediscono alla legge di Ohm solo quando la temperatura è mantenuta
costante durante la misura.
Resistività e coefficienti termici per alcuni materiali
Vari tipi di resistori
Codice colori
1. Trovare la carica che passa in un giorno attraverso una sezione di un conduttore in
cui circola una corrente costante di 0.5A.
Risoluzione:
Poiché l’intensità di corrente è definita come la carica che passa nel
conduttore in un secondo, allora la carica che passa in un giorno è: Q = I°t = 0,5 A° (24°3600
s) = 43200 C
2) Se si collegano due pile, in modo che il polo negativo dell’una sia a contatto con
quello positivo dell’altra, e quello positivo dell’una sia a contatto con quello negativo
dell’altra cosa succede?
Risoluzione:
Le due pile sono in corto circuito e si scaricano rapidamente l’una
sull’altra.
Esercizi sulla legge di Ohm
3) Calcolare la d.d.p. che si deve applicare ai capi di un conduttore di resistenza 500kΩ
affinché esso venga percorso da una corrente di intensità 4mA.
Risoluzione:
Innanzitutto occorre esprimere i valori di resistenza e intensità di
corrente in ohm e ampere:
500kΩ = 5°105Ω e 4mA = 4°10-3A e , quindi, applicando
la prima legge di Ohm, si trova che ΔV = Ri = 2°103V.
4) Un filo lungo 50 m e di sezione 4 mm2 ha una conduttività di 4•105 siemens/m. Calcolare
l’intensità della corrente che percorre il filo quando ai suoi estremi viene applicata la d.d.p. di 300
V.
Risoluzione: Innanzitutto, occorre che tutti i dati siano espressi nelle unità di misura del Sistema
Internazionale, usando la notazione scientifica, in particolare A=4°10-6m2 Quindi, essendo la
conduttività l’inverso della resistività r, si ha che:  =
1
1
=
 2,5  10  6 m
 4 10 5 siemens/m
Applicando la seconda legge di Ohm, si determina la resistenza:
R
l
50m
= 2,5  10  6 m
 31,25
-6
2
S
4  10 m
Di qui, per la prima legge di Ohm, si trova la corrente:
i
V
300V
=
 9,6 A
R
31,25
5) I poli di un generatore di f.e.m. 50 V sono collegati ai capi di un circuito. La corrente che
attraversa il circuito è di 0.5 A e la resistenza esterna è 60 . Calcolare il valore della resistenza
interna del generatore.
Risoluzione:
Il generatore ha anch’esso una resistenza interna, R°i ,che contribuisce a
determinare la corrente nel circuito, cioè: f.e.m. =(R+Rint) i Da qui è possibile ricavare il valore della
resistenza interna al generatore:
R int 
f.em.
50V
-R =
 60  40
i
0,5A