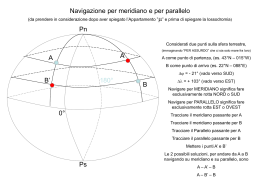
L’Appartamento
m
“Distanza in miglia nautiche tra
due punti aventi la stessa
latitudine”
Semplice spiegazione utilizzando le proprietà della trigonometria piana
e della trigonometria sferica.
Nella trigonometria piana…
…sulla terra
90°
b
Pn
a
cos a
b
R * cos j
a’
j’
R * sen j
sen a
a
cos a
a = posizione sulla terra
0°
j
C
R * cos j
equatore
Se facciamo passare una parallela al coseno
passante per il punto di intersezione del raggio
con la circonferenza (punto a), si può notare
come (per il principio degli angoli alterni interni
determinati da una retta secante due rette
parallele), l’angolo a’ sia uguale ad a ed il tratto
a-b corrisponda al coseno
Consideriamo ora due punti sulla terra aventi la stessa latitudine: a e a’ (ja = ja’). Disegnamo
prima le due sezioni come nella lastrina precedente….
…poi disegnamo l’appartamento (m) e la differenza di longitudine (Dl)
Pn
I due triangoli sferici a’ba e d’cd sono simili in quanto
hanno un angolo in comune (g) e due lati rispettivamente
uguali fra loro (cioè sono triangoli sferici isosceli)
b
g
a’
m
a’
a
m
j
g
g
a
c
c
b
d’
d
Dl
j
g
d’
d
Dl
…pertanto i loro lati sono simili e proporzionali fra loro.
Possiamo infatti scrivere:
(R * cosj): R = m : Dl
m * R = Dl * R * cosj
equatore da cui si ricava…
...e infine (dividendo tutto per R)
m = Dl * cosj
...per calcolare m in miglia
m = |Dl’| * cosj