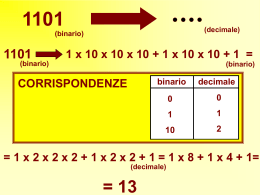
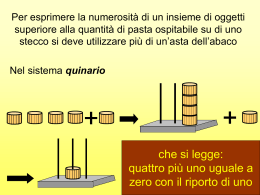
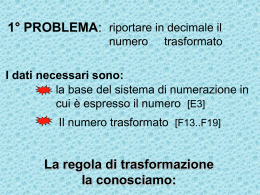
decimale
quinario
317
2232
Conosciamo le regole per trasformare un
numero quinario in decimale
Applichiamole anche alla
trasformazione inversa
….
317
(quinario)
(decimale)
317
(decimale)
3 x 10 x 10 + 1 x 10 + 7 x 1
(decimale)
3 x 20 x 20 + 1 x 20 + 12 x 1
(quinario)
3 x 400 + 20 + 12
(quinario)
2200 + 20 + 12
(quinario)
2232
(quinario)
Il conteggio fatto presuppone la competenza
d’operare con le regole della somma e della
moltiplicazione relative al sistema di
numerazione in cui deve essere espresso il
risultato
E’ molto più economico disporre di
un procedimento che, avvalendosi
delle regole del sistema decimale,
effettui la trasformazione voluta
Riprendiamo l’abaco per quantificare,
in quinario, 317 pezzi di pasta
317
Tutta la pasta non può essere ospitata sul
primo stecco di destra [quello delle unità]
Per esprimere la numerosità dei pezzi di pasta
utilizzeremo una procedura che utilizza, come
unità di misura, quello dello stecco più a
sinistra [quello delle cinquine]
63
Rieseguiamo la
procedura sul numero
delle cinquine
12
e, infine
317
(decimale)
2232
(quinario)
Le cifre che compongono il numero quinario
si ottengono, iniziando da quella più a destra,
calcolando il resto della divisione [decimale] tra
le quantità di oggetti [espressi in decimale] e cinque
Applichiamo la regola al caso appena risolto:
317 : 5 = 63
col resto 2
63 : 5 = 12
col resto 3
12 : 5 =
2
col resto 2
2 : 5 =
0
col resto 2
Il numero, che si legge seguendo la
direzione indicata dalla freccia, è il risultato
Si prendano una bilancia a due piatti
e un certo numero di palline
Su questi si distribuiscano le palline
Terminata l’operazione i due piatti devono
risultare in equilibrio
Su un foglio scriveremo
zero se tutte le palline sono sulla bilancia
uno se l’equilibrio è stato ottenuto
togliendone una
L’operazione sarà ripetuta, con le palline di
un solo piatto, fino a che non le avremo
esaurite tutte
Ad esempio:
Quante sono
le palline?
1
0
1
Pensateci a
casa.
Ne parleremo
nel prossimo
incontro
0
0
1