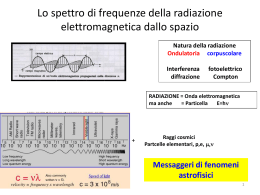
Corso di Fondamenti di Astronomia e Astrofisica
Docente: Prof. Nichi D’Amico
1. Lezioni introduttive
• Ordini di grandezza in Astrofisica. Cosa conosciamo nell’Universo
• Gli obiettivi scientifici, il metodo e le applicazioni dell’Astrofisica
• Lo spettro elettromagnetico. Radiazione da corpo nero
• Emissione termica e non termica
• Principi di funzionamento dei telescopi. Diffrazione e risoluzione angolare in banda
ottica e in banda radio
• Misure fondamentali in Astrofisica: Misure di flusso. Magnitudine. Misure di colore.
Misure di distanza. Parallasse. Misure indirette di distanza. Misure di moto proprio.
Misure Doppler.
• Dimensioni di Terra, Luna e Sole e distanze reciproche: l’approccio degli antichi Greci
Durante il Corso useremo in generale il sistema cgs (centimetro grammo secondo)
Ordini di grandezza in Astrofisica
Oggetto
Dimensioni
(cm)
Massa
(gm)
Terra
109
1028
Sole
1011
1033
Galassia
1023
1045
Universo Oss.
1028
1055
1 pc = 3.09 x 1018 cm
(è la distanza di una stella la cui parallasse annua è di un arcsec)
1 anno luce = 9.5 x 1017 cm (è la distanza percorsa dalla luce in un anno)
1 AU = 1.5 x 1013 cm (distanza media Terra-Sole)
Cosa conosciamo nell’Universo
• Stelle (il Sole è un ottimo esemplare di stella “tipo”)
Massa M = 1.99 x 1033 gm
Raggio R = 6.96 x 1010 cm
Luminosità = 3.9 x 1033 erg s-1
Distanza = 1 A.U. = 1.5 x 1013 cm = 500 secondi-luce
• Stelle estese (per esempio Giganti Rosse)
Rappresentano il primo passo evolutivo di una stella del
tipo del Sole. Possono raggiungere dimensioni fino a 10
100 volte quella del Sole.
• Nane Bianche
Stadio finale di una stella del tipo
del Sole. Dimensioni pari 1/100
del Sole, massa pari a qualche
frazione di massa solare
• La maggior parte delle stelle nella Galassia sono stelle singole o stelle “doppie”.
• Un esempio famoso di stella doppia è Sirio, in quanto costituisce la prima
osservazione di una Nana Bianca (Sirio-B)
• Ci sono tuttavia nella Galassia casi in cui centinaia o migliaia di stelle sono
raggruppate in ammassi, cosiddetti Ammassi Aperti. Un famoso ammasso aperto è
l’ammasso delle Pleiadi
• Le stelle più vecchie nella Galassia si trovano
invece in altri tipi di ammassi, detti Ammassi
Globulari. Un ammasso globulare può contenere
anche più di un milione di stelle.
• Nella Galassia, lo spazio fra le stelle non è spazio vuoto, ma contiene materia
allo stato diffuso denominata Mezzo Interstellare.
• Nel mezzo interstellare troviamo nubi di polvere, ma anche raggi cosmici
energetici, la cui traiettoria può essere condizionata dalla presenza di campi
magnetici.
NGC1999, una nebulosità nella costellazione di Orione.
Si tratta una cosidetta “reflection nebula”, una nube di
polvere che circonda una stella di cui riflette la luce
• Nebulose di gas fluorescente in zone di formazione stellare sono abbastanza
comuni
La Trifid Neabula, distante circa 9000 anni
luce. Si tratta di una regione di elevata
formazione
stellare.
Osservazione
effettuata con il telescopio HST
• Altri oggetti “appariscenti”, come la Nebulosa del Granchio, sono sorgenti di un
particolare tipo di radiazione, detta radiazione di sincrotone.
• Oggi sappiamo che oggetti come la Nebulosa del Granchio sono ciò che
rimane dopo l’esplosione di una Supernova, l’evento catastrofico che segna la
fine di una stella la cui massa originaria era di diverse masse solari
• Ma sappiamo anche che in una esplosione di Supernova il nucleo centrale della
stella originaria collassa e può formare una “Stella di Neutroni” o un “Buco
Nero”.
• Altre stelle, quelle di massa paragonabile a quella del Sole finiscono la loro
vita in modo assai meno violento, seguendo una lenta evoluzione che alla fine
porta alla formazione di una “Nana Bianca”
• Le stelle, e il materiale diffuso che troviamo fra le stelle, cioè il mezzo
interstellare, vivono in giganteschi sistemi denominati galassie. La nostra
Galassia, la Via Lattea, ne è un esempio.
• La nostra Galassia, a sua volta fa parte di un gruppo di galassie denominato
Gruppo Locale, contenente una dozzina di galassie.
• La nostra Galassia e la galassia
Andromeda sono le galassie più grandi
del Gruppo Locale. Andromeda dista da
noi 2 milioni di anni luce
• A parte i piccoli gruppi di galassie, come il nostro “Gruppo Locale”, le galassie si
trovano anche raggruppati in giganteschi Ammassi di Galassie, ognuno dei quali
può contenere migliaia di galassie
Il Coma Cluster, distante circa 350 000 000 di anni luce, contiene migliaia di galassie
• Molte delle galassie che si trovano in un Ammasso sono del tipo “ellittico”
Virgo-A una galassia ellittica gigante nel Virgo Cluster
Distanza: 60 000 000 anni luce
Contiene circa 1012 Masse Solari di materia
• Mentre la maggior parte delle galassie che si trovano in un generico campo di
cielo sono il tipo più comune di forma a “spirale”
La galassia a spirale M83
Distanza: 25 000 000 anni luce
• Ammassi di galassie sono stati trovati fino a distanze di alcuni miliardi di anni
luce.
Gli obiettivi scientifici dell’Astrofisica
• C’è certamente un aspetto descrittivo, di censimento.
• Applicare le leggi della Fisica per capire il funzionamento dei corpi celesti
e dell’Universo nel suo insieme  Approfondire la conoscenza
• Utilizzare le condizioni fisiche “estreme”, non riproducibili sulla Terra, che
sono presenti in alcuni corpi celesti come laboratorio di verifica delle leggi
fondamentali della Fisica
Ma nell’uso di questo laboratorio cosmico per la verifica di leggi fondamentali,
c’è una differenza essenziale di metodo fra la Fisica e l’Astrofisica:
• In Fisica possiamo preparare un esperimento
• Possiamo cambiare i parametri dell’esperimento
• Possiamo cambiare i valori di alcune grandezze e verificare le variazioni di
quei parametri che da queste dipendono
• In Astrofisica, possiamo solo “stare a guardare”
• In linea di principio, in Astrofisica non esiste possibilità di ripetere una misura
• Nonostante questo, la possibilità che offre l’Astrofisica di studiare la
materia in condizioni estreme, non riproducibili in laboratorio offre una
prospettiva unica di verifica di leggi fondamentali.
• Per esempio, le migliori verifiche della Teoria della Relatività Generale
provengono da osservazioni e studi di Astrofisica
L’Astrofisica si avvale oggi di tecnologie d’avanguardia
in una varietà di settori:
• Informatica, tecniche di calcolo, ricostruzione immagini, algoritmi di calcolo
distribuito
• Elettronica, microonde, signal processing
• Tecnologie criogeniche
• Ottica di precisione
• Meccanica di precisione
In questo contesto, la realizzazione di uno dei più imponenti impianti
dell’Astrofisica moderna in Sardegna, il Sardinia Radio Telescope
(SRT), rappresenta una grande occasione si sviluppo scientifico e
tecnologico e di alta formazione
Diametro del paraboloide 64 m
Altezza della struttura meccanica 80 m
Range di frequenza 0.3 – 100 GHz
3 posizioni focali
Peso 3000 tonnelate
Lo spettro elettromagnetico
Oggi in Astrofisica si effettuano osservazioni a tutte le lunghezze d’onda
Comportamento termodinamico della radiazione: Emissione termica –Legge di Planck
Sappiamo che la radiazione emessa alle varie lunghezze d’onda da un corpo
sufficientemente opaco (corpo nero) a temperatura T obbedisce alla legge di Planck:
B(T) = (2hc2/5) /(ehc/kT -1)
dove:
B(T) = Intensità monocromatica specifica
B(T) = Potenza emessa alla lunghezza d’onda 
• per unità di area
• per unità di angolo solido
• per unità di lunghezza d’onda
Legge dello spostamento di Wien
maxT = 0.29 cm °K

T
Legge di Stefan-Boltzmann
Dalla legge di Planck deriva che la densità di energia (erg cm-3) del campo di
radiazione in un corpo nero è data da:
Erad = aT4
e che il flusso di energia che lascia la superficie del corpo nero (erg cm-2 s-1) è dato
da:
f =  T4
dove:
 = ca /4
Costante di radiazione a= 7.56 x 10-15 erg cm-3 °K-4
Costante di Stefan-Boltzmann  = 5.67 x 10-5 erg cm-2 s-1 °K-4
f
• Nelle formule di Stefan-Boltzmann:
Erad = aT4
(erg cm-3)
f =  T4 (erg cm-2 s-1)
la temperatura T è la stessa e si riferisce alla temperatura ideale di corpo nero, cioè
un corpo opaco, in cui quindi il campo di radiazione e la materia sono in equilibrio.
• Un qualsiasi corpo a temperatura T, per il semplice fatto che irradia, non è in
equilibrio
• Possiamo immaginare che una buona approssimazione del corpo nero ideale sia
un forno perfettamente isolato dall’Universo, a temperatura interna T, con un piccolo
foro da, quale possiamo misurare la radiazione:
T
Te

• In questo caso, definiamo una temperatura efficace Te, come la temperatura
superficiale che il forno avrebbe se fosse un corpo nero ideale con uno spettro di
radiazione uguale a quello della radiazione osservata  f =  Te4
Quindi, per esempio in una stella:
• misuriamo lo spettro della radiazione
• se è sufficientemente “simile” a uno spettro di
corpo nero, possiamo associarlo a una
temperatura T
• Questa è la temperatura superficiale effettiva
Te, “quella il cui colore prevalente è il colore
della stella”
• A questa Te corrisponde un flusso superficiale
f =  Te4
• Ma, come vedremo, questa non è certo la
temperatura media all’interno della stella !
• Quindi nel caso reale di una stella, in generale:
Tm Te
T = 5800 °K
Processi termici di emissione (e assorbimento)
Free-free
(Bremsstrahlung)
Transizioni atomiche
In Astrofisica abbiamo anche modo di osservare fenomeni di
emissione di radiazione non termici
Emissione da Sincrotrone
Sincrotrone
Corpo Nero
Gli strumenti astronomici a varie lunghezze d’onda
• Questa è una prima –breve- rassegna delle varie tipologie di strumenti
astronomici di cui disponiamo oggi e dei parametri fisici che li caratterizzano.
• In alcune lezioni successive, più avanti nel Corso, approfondiremo alcuni
aspetti di alcuni di questi strumenti
Cominciamo con la descrizione di massima di un telescopio
Lo scopo principale di telescopio è quello di raccogliere “una grande quantità
di radiazione” utilizzando quindi una grande area di raccolta, e focalizzarla in
un’area relativamente piccola, accessibile agli strumenti di misura
Immagine “puntiforme”
Sorgente
puntiforme
all’infinito
f = erg cm-2 s-1
Area di raccolta
Dispositivo di
misura
Per focalizzare la radiazione si può utilizzare il fenomeno della rifrazione
(uso di lenti) , o quello della riflessione (uso di specchi)
Rifrazione: velocità va di propagazione della luce in un dato mezzo va < c
e in generale va  vb
Le lenti funzionano in base alla diffrazione
Ma soffrono del fenomeno di
aberrazione cromatica
vm = vm()
vm = vm()  è però utile per esaminare lo spettro della radiazione
Il fenomeno della riflessione
Perpendicolare alla superficie riflettente
Raggio riflesso
Raggio incidente
i
r
Superficie riflettente
i = r
A livello microscopico, il fenomeno è dovuto alla presenza, nel metallo, di elettroni liberi
non legati al reticolo (stesso motivo per cui i metalli sono buoni conduttori). Questi
elettroni liberi costituiscono una vera e propria barriera elettromagnetica, nel caso di
radiazione di lunghezza d’onda adeguatamente lunga
Uso della riflessione (specchi)
(utilizzato non solo nella banda visibile, ma anche in X e radio)
specchio parabolico
fuoco
raggi paralleli provenienti da una sorgente
puntiforme a distanza infinita
f
lunghezza focale
Ma perché lo specchio deve necessariamente essere parabolico ?
Riepiloghiamo le proprietà di una ellisse:
f1
f2
In un ellisse, la bisettrice dell’angolo formato dai due segmenti che uniscono un dato
punto dell’ellisse ai due fuochi, è sempre perpendicolare alla tangente all’ellisse nel
punto in considerazione.
Quindi: in uno specchio a forma di ellisse, un qualsiasi raggio generato in un dato
fuoco viene riflesso nell’altro fuoco.
f1
f2
specchio ellittico
Uno specchio ellittico riproduce nel fuoco f1 l’immagine di una sorgente
puntiforme posta nel fuoco f2
Se allontaniamo i due fuochi a distanza infinita, l’ellisse diventa una parabola
e i raggi provenienti da distanza infinita sono paralleli
f
Uno specchio parabolico riproduce nel suo a fuoco l’immagine di una
sorgente puntiforme a distanza infinita
Figura di diffrazione dell’apertura e
potere risolutivo di un telescopio
• L’immagine nel piano focale di una sorgente puntiforme posta
all’infinito NON è un punto come vorrebbe l’ottica geometrica,
ma è la figura di diffrazione dell’apertura.
• In particolare si dimostra che la figura di diffrazione che si
ottiene nel piano focale è la Trasformata di Fourier della
funzione che descrive apertura
A
Questo fatto limita il potere risolutivo del telescopio, cioè la sua capacità di
risolvere due sorgenti puntiformi
e di conseguenza la sua capacità di risolvere al di sotto di una certa scala
angolare i dettagli di una sorgente estesa
x/ f
Le dimensioni fisiche della figura di diffrazione sul
piano focale dipendono invece dalla distanza focale
 /A
La risoluzione angolare dipende solo dal
rapporto /A
Risoluzione angolare nominale tipica di un telescopio ottico di medie dimensioni:
  5 x 10-5 cm (5000 Å)
A=5m

0.03 arcsec
In questo caso il limite effettivo è rappresentato dalla turbolenza dell’atmosfera
Le migliori condizioni di “seeing” sulla terra si ottengono oggi a Mauna Kea, sito a
4200 mt nelle Haway (0.2”)
Risoluzione angolare nominale tipica di un radiotelescopio di medie dimensioni
  21 cm
A = 32 m
 28 arcmin
In questo caso il limite effettivo è proprio la diffrazione
Oculare
fuoco
Configurazioni tipiche dei telescopi ottici
Dispositivi per campionare il piano focale di un telescopio ottico
• Oculare
• Lastra fotografica
• Dispositivo CCD  Immagine digitale  risoluzione angolare e temporale
• Spettrometro  dati digitali  risoluzione spettrale e temporale
Configurazioni tipiche dei radiotelescopi
Parkes 64mt 400 MHz – 10 GHz
(70cm
3cm)
 = 14 arcmin a 1.4 GHz (21cm)
f/0.4
Fuoco primario
Noto 32 mt 650 MHz – 45 GHz
(50cm
7 mm)
 = 28 arcmin a 1.4 GHz (21cm)
f/1.0
Fuoco secondario (Cassegrain)
SRT 64 mt 300 MHz 100 GHz
(90cm
3mm)
 = 14 arcmin a 1.4 GHz (21cm)
Fuoco secondario (Gregoriano)
f/0.37
f1.3
f2.3
Dispositivi di campionamento del piano focale in radioastronomia
Feed
preamplificatore
Questo equivale in un telescopio ottico ad un “pixel” della lastra fotografica
o del dispositivo CCD !!
Specchi per Astronomia X
Radiazione a lunghezze d’onda molto corta come nel caso dei raggi X, penetra
la superficie dei metalli senza quindi essere riflessa. Si può tuttavia ottenere
riflessione per “incidenza radente” per un range relativamente limitato di
lunghezze d’onda (10 kEv).