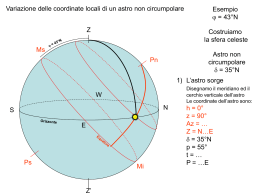
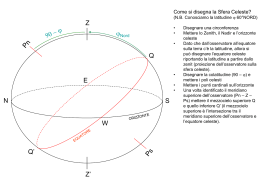
Astro circumpolare e astro non circumpolare Z j Costruiamo la sfera celeste… Ricordiamo che il meridiano superiore dell’osservatore è quello che parte dal Pn Pn celeste, passa per lo zenith ed arriva al Ps celeste (in pratica è la proiezione del meridiano dell’osservatore sulla sfera celeste) l’opposto (che N Ovviamente unisce i poli passando per il nadir) è il meridiano inferiore dell’osservatore (proiezione del suo antimeridiano) Ms W S E Ps Mi Z’ Esempio: j = 25°N Esempio: j = 25°N Astro circumpolare e astro non circumpolare Z j coj Ms Astro circumpolare W S E d Ps Mi Z’ Per un osservatore con tale latitudine, quale declinazione minima deve avere un astro per poterlo definire “circumpolare”? Considerando che dallo zenith al polo Pn nord c’è la colatitudine (coj = 90 – j) Considerando che dallo zenith j all’orizzonte sono ovviamente 90 gradi …allora l’angolo che va dal Polo nord all’orizzonte (al punto cardinale Nord) N corrisponde alla latitudine …allora l’angolo che va dal punto cardinale nord al mezzocielo inferiore corrisponde alla colatitudine …ma quest’ultimo angolo corrisponde anche alla minima declinazione che un coj astro deve avere per essere circumpolare …allora un astro per essere circumpolare deve avere una declinazione maggiore della colatitudine (la declinazione deve avere lo stesso segno del polo elevato). Tale astro non sorge né tramonta Esempio: j = 25°N Astro circumpolare e astro non circumpolare Z Dalle effemeridi prendiamo tre astri di esempio Ms Pn d = 74°N d = 19°N d = 17°S Vediamo come ciascuno di questi astri si muove sulla sua orbita… W S E Ps Mi Z’ 1) Kochab 2) Arturo 3) Sirio Kochab è un astro circumpolare quindi non sorge né tramonta N ma passa sia sul meridiano superiore dell’osservatore che sul meridiano inferiore Arturo non è un astro circumpolare quindi sorge, tramonta e passa solamente sul meridiano superiore dell’osservatore Sirio non è un astro circumpolare quindi sorge, tramonta e passa solamente sul meridiano superiore dell’osservatore. Appartiene all’emisfero SUD, quindi rimane per meno tempo sopra l’orizzonte. Esempio: j = 25°N Analisi dell’orbita di un astro NON circumpolare j d Analizziamo l’orbita di ARTURO (astro non circumpolare) d = 19°N Z z Vediamo i casi particolari dell’orbita: Ms - Arturo sorge. - L’amplitudine al sorgere (ortiva) è data dalla formula senAM = send/cosj = sen19/cos25 senAM = 0,3255681/0,9063078 senAM = 0,3592246 AM = E 21° N h Pn W amplitudine N S E amplitudine - Arturo passa in meridiano - La latitudine dell’osservatore può essere facilmente ricavata grazie alla formula deducibile dal disegno j = z + d = 90-h + d - Arturo tramonta - L’amplitudine al tramonto Ps Z’ Mi (occasa) è calcolabile come la precedente, solo che cambia il prefisso AM = W 21° N Esempio: j = 25°N Analisi dell’orbita di un astro circumpolare (per essere più chiari serve un ingrandimento) j d Analizziamo l’orbita di Kochab (astro circumpolare) d = 74°N Vediamo i casi particolari dell’orbita: h j S h d - Kochab passa in meridiano SUPERIORE - La latitudine dell’osservatore può essere facilmente ricavata grazie alla formula deducibile dal disegno j = h + d - 90 - Kochab passa in meridiano INFERIORE - La latitudine dell’osservatore può essere facilmente ricavata grazie alla formula deducibile dal disegno j = 90 - d + h Considerazioni banali ma necessarie 1) A meno che non si tratti del sole o della luna, il sorgere ed il tramonto di un astro (e quindi l’uso della amplitudine per il controllo della bussola) sono praticamente impossibili da rilevare 2) Il passaggio in meridiano di un astro (sempre a meno che non si tratti del sole o della luna) per essere sfruttato come controllo della latitudine, deve avvenire “ovviamente” durante il crepuscolo perché è necessario misurare l’altezza dell’astro Considerazioni importanti sull’emisfero nord celeste Polaris 5 Polo nord 4 3 2 1 …ecco perché l’azimuth della polare quasi mai è proprio NORD e l’altezza vera della polare non corrisponde esattamente alla latitudine ma è necessario fare 3 correzioni dovute proprio a tale “minuscola” distanza polare Se fossimo proprio sul Polo nord, avremmo proprio il polo nord celeste in corrispondenza dello zenith, le stelle sarebbero tutte circumpolari e si muoverebbero così (nel disegno ci sono quelli con declinazione d maggiore di 45°)… Il metodo per riconoscere la stella polare (dato che l’orsa minore è poco visibile a parte la polare) è il seguente: • Riconoscere le sette stelle più visibili della costellazione ORSA MAGGIORE • Prolungare di cinque volte la distanza tra le ultime due stelle Se ingrandiamo la stella polare …e la facciamo ruotare… …scopriamo che essendo la sua declinazione 89° e 16’, in effetti essa non corrisponde esattamente al Polo Nord ma ci ruota molto vicino (distanza polare 44’) Ovviamente il tutto non è percettibile per l’occhio umano Spiegazione grafica di quanto l’altezza della polare corrisponda (dopo 3 piccole correzioni già descritte nella lastrina precedente) alla latitudine j coj Z Esempio: j = 25°N Costruiamo la sfera celeste… Ms W S E Ps Mi Z’ Posizioniamo la stella polare L’altezza della stella polare si Pn avvicina molto all’arco di h meridiano inferiore compreso tra il Polo nord celeste e l’orizzonte celeste. Se tra lo zenith e il punto N cardinale nord dell’orizzonte ci sono 90° … …e tra il Polo Nord ed il mezzocielo superiore sono sempre 90°…. …allora sono uguali i due archi tra zenith e mezzocielo superiore (j) e tra polo nord e punto cardinale nord… …perché complementari dello stesso angolo (90-j) Considerazioni importanti sull’emisfero sud celeste Polo sud 4 3 2 1 Se fossimo proprio sul Polo sud, avremmo proprio il polo sud celeste in corrispondenza dello zenith, le stelle sarebbero tutte circumpolari e si muoverebbero così (nel disegno ci sono quelli con declinazione d maggiore di 45°)… Dato che, purtroppo, non c’è una stella molto vicina al polo sud che sia adeguatamente visibile (come la polare per il polo nord) il metodo per identificare più o meno la sua posizione è il seguente: • Riconoscere la costellazione CROCE DEL SUD (molto visibile) • Prolungare di quattro volte il suo asse maggiore dalla parte della base della croce romana
Scaricare