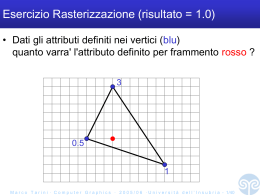
Pajek
Download:
http://vlado.fmf.uni-lj.si/pub/networks/pajek/
Corso Pajek Sidney 2105
http://vlado.fmf.uni-lj.si/pub/networks/doc/seminar/NICTA.htm
DATA SETS:
http://vlado.fmf.uni-lj.si/pub/networks/data
Pajek significa «ragno» in Sloveno.
Pajek è un software per la visualizzazione e l’analisi delle reti
complesse.
E’ continuamente esteso e aggiornato.
Gli autori sono: Vladimir Batagelij e Andrei Mrvar dell’università di
LjublJana (Slovenia)
libro
libro
Manuale
la social network analysis (SNA) permette di rispondere a domande molto
semplici ma importanti quali:
•chi conosce chi
•chi ha il numero più elevato di contatti in una comunità o
organizzazione
•quali sono i sotto-gruppi di cui è composta una comunità numerosa
•come funziona l'organizzazione reticolare di un movimento politico
o di un gruppo terrorista
•come sono collegati tra loro i dirigenti di aziende quotate in borsa
•ecc.
Introduzione all SNA
http://www.ccsr.ac.uk/methods/publications/snacourse/snacourseweb.html
introdurre reti
rappresentare graficamente le reti
Statistica di base
come si misura la coesione
Main window
Aprire una rete esistente
Disegnarla
Dining-table_partners.net: 26 vertices, 52 valued arcs (1 =
first choice, 2 = second choice), no edges, no loops.
1. Creare un file (*.net, *.vec, *.clu) manualmente con Pajek
Net/RandomNetwork/Total n° of Arcs(es: 15 , How many arcs=10)
File/Network/Edit (cambia un vertice per volta)
Partition/Create Constant PartitionFile/Partition/Edit
Vector/Create Constant VectorFile/Vector/Edit
File/Network/Save
File/Partition/Save
File/Vector/Save
2. Modificare un file manualmente con un word processor
Net/Random Networks/Total n° of arcs (es: 15 , How many arcs=10)
File/Network/Save Open file with Blocco Note and modify it
Save Re-open File before using it (Never use TAB)
Analogamente per partizioni e vettori
Come inserire una rete: Esempio 1
Mario
Pippo
Franco
Giovanni
Luca
*Verteces 5
1 «Pippo»
…
*matrix
00001
00011
00010
01101
11010
*Verteces 5
1 «Pippo»
2 «Franco»
3 «Luca»
4 «Giovanni»
5 «Mario»
*Edges
15
25
24
34
45
* Arcs
2. Lista di vertici seguita da una matrice.
Limitazioni: non è possibile indicare linee multiple
Linee di valore 0 = non linee
*Verteces 5
1 «Pippo»
2 «Franco»
3 «Luca»
4 «Giovanni»
5 «Mario»
*Arcslist
15
254
34
45
1. Lista di vertici seguita da
una lista di arcs/edges
Possono essere ni reali
Esempi di grafi diretti(digraph)
Drawing
Draw
Draw/Partition
Draw/Vector
Draw/Partition/Vector
Draw/Layout/circular
Draw/Layout/Energy/Kamada-Kaway/Free
Per default Pajek non disegna reti con più di
5000 vertici anche se può fare i calcoli con reti
di 9.999.997 vertici
L’algoritmo di Kamada –Kawai trova la posizione dei nodi che minimizza il numero di incroci
delle linee e la distanza tra i nodi.
Drawing
La posizione dei vertici può essere cambiata usando il mouse.
Si possono usare le Option dalla finestra grafica per visualizzare diversamente i nodi e
gli archi.
Le figure si possono esportare con export o copiando la foto (print screen) in Paint
Statistica di base su reti unimodali
Info/Network/General
fornisce informazioni generali sulla rete:
m=n°spigoli, n=n° nodi; <k>=2m/n grado medio
Densità1= d1=m/(n*n)=link esistenti/link possibili (con loops)
Densità2=d2=m/(n*(n-1))=link esistenti/link possibili (senza loops)
Esercizio
Inserire la seguente rete che rappresenta «chi è amico con chi» all’interno di un gruppo sportivo
1 nessuna frequentazione
2 frequentazione saltuaria (1 v al mese)
3 frequentazione assidua (1 v alla settimana)
1.Laura (15)
0 1 2 1 1 1 1 3 1 1 1 1
• Creare il file es1 .net
• Rendere la rete non
diretta
• Inserire la rete come
matrice e come lista
• Creare la partizione
maschi/femmine
• Creare il vettore età
0 0 2 2 2 1 1 1 1 1 1 1
0 0 0 1 1 1 1 1 1 1 1 1
2.Michela (16)
3.Emanuela (14)
0 0 0 0 1 1 1 2 3 1 2 3
4.Silvia (12)
0 0 0 0 0 2 1 1 1 3 1 3
5.Roberta (17)
0 0 0 0 0 0 1 1 2 3 1 2
6.Giovanna (15)
0 0 0 0 0 0 0 1 1 3 2 2
7. Giorgio(12)
0 0 0 0 0 0 0 0 1 2 3 3
8. Carlo(14)
0 0 0 0 0 0 0 0 0 1 2 1
9. Marco(15)
0 0 0 0 0 0 0 0 0 0 1 1
10. Leonardo (17)
0 0 0 0 0 0 0 0 0 0 0 2
0 0 0 0 0 0 0 0 0 0 0 0
11. Davide(15)
12. Luca 16)
Statistica di base
Info/network/general (0)
Info/partition (0)
Info/vector (0)
Come misurare la Coesione
A cosa può servire misurare la coesione?
Prevedere la diffusione di idee/innovazioni e l’uniformità di tale diffusione
E’ più probabile avere diverse opinioni in diversi gruppi coesi.
K-cores
E’ il massimo sotto-grafo connesso in cui ogni nodo è connesso con
almeno altri k-nodi nel gruppo.
A volte questo è un concetto troppo stringente per individuare comunità in una rete.
Può essere interessante osservare la sovrapposizione fra diversi k-cores
Net/Partitions/core
P-cliques= percentuale delle connessioni
E’ il massimo sotto grafo connesso in cui i nodi hanno almeno una data percentuale p di vicini
all’interno del sotto grafo
Problema: si può avere p alto se molti vertici appartengono ad un grande cluster
Altri metodi:
Componenti connesse (strong e weak)
Densità dei link nella rete
Esempio con Pajek.
Attiro.net
Nel 1948 i sociologi americani studiarono le relazioni sociali in una regione della Costa Rica nel
Sud America. Essi erano interessati all’impatto delle relazioni sociali sull’evoluzione di una
società. Studiarono le relazioni di «fare visita a» tra famiglie che vivevano nelle «haciendas»
(fattorie). La rete di visite è contenuta nel file Attiro.net. Si ha un semplice grafo diretto dove
ogni arco rappresenta la frequenza delle visite da una famiglia ad un’altra. Non si conosce
l’esatto numero di visite. Le linee sono classificate come «ordinarie» (1), visite saltuarie tra
famigliari (2), visite ricorrenti tra famigliari (3). I loops non ci sono perché in questo caso non
hanno senso
La visualizzazione
aiuta a mettere in
evidenza le diverse
famiglie e la forza dei
loro legami. Le
famiglie verdi e
azzurre sono
concentrate al
centro. Eccezione
f43
Che gruppi coesi possiamo trovare in attiro.net? Coincideranno con le famiglie?
Per misurare la connessione si può misurare la densità dei link
Net/Info/General (0)
La rendo non diretta perché così il grado è il numero di vicini
Net/Transform/Arcs-Edges
Net/Partition/Degree
Info/Partition
Rete non diretta
Net/partitions/Core/(all)
Draw/Draw partition
I colori dei vertici indicano il
più grande k-core a cui i
vertici appartengono
3 k-core
Sembra che i k-core non
identifichino i
raggruppamenti delle
famiglie
p-Cliques
Partizione della rete in sotto-grafi i cui vertici hanno una percentuale almeno di p di vicini
P=0.5
Nemmeno le p-cliques identificano
I raggruppamenti tra famiglie
Strongly connected component with Pajek
Attiro.net (CAP 3) sono importanti le strong component (=gruppi che si visitano a
vicenda) sono quindi importanti le direzioni delle frecce
Net/Component/Strong
Draw/Draw Partitions
Layout/circular/using Partition
Se vi si sovrappone la partizione in famiglie si ottiene:
Quindi le strong component individuano le famiglie