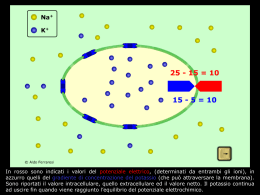
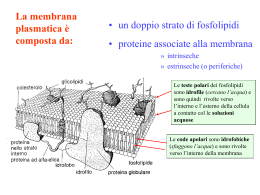
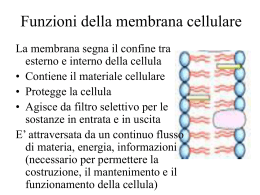
Tutte le cellule (non solo le cellule eccitabili)
hanno un potenziale di riposo (resting): una carica
elettrica attraverso la membrana plasmatica, con
l’interno della cellula negativo rispetto all’esterno. Il
valore del potenziale di riposo varia, ma nelle cellule
eccitabili si aggira tra -90 e -70 mV.
Il potenziale di membrana di un neurone a riposo
misura circa -70 millivolt (mV), cioè il potenziale di
un neurone all’interno della cellula è minore di
circa 70 mV rispetto al liquido extracellulare. Il
neurone allo stato di riposo è polarizzato.
Il potenziale di riposo origina da:
a) Ineguale distribuzione delle specie ioniche tra il
liquido extracellulare ed intracellulare:
INTRA (mM)
EXTRA (mM)
Na+
12
145
K +
150
4,1
Ca2+
10-7 (M)
3
Cl -
4
118
A-
146
1
CATIONI:
ANIONI:
b) Differente permeabilità della membrana ai
diversi tipi di ioni:
allo stato di “resting”, gli ioni potassio (K+) possono
attraversare la membrana facilmente, mentre ioni
cloro (Cl-) e sodio (Na+) presentano molte difficoltà.
Le grosse molecole proteiche si comportano come
ioni carichi negativamente (A-) e non attraversano la
membrana.
Due forze agiscono su una particella carica:
La FORZA DI
DIFFUSIONE,
generata dal gradiente
di concentrazione
La FORZA ELETTRICA,
generata dal gradiente
elettrico
La concomitanza di queste due forze spinge il flusso
ionico all’interno o all’esterno della cellula.
Cosa accade alla membrana quando è permeabile ad un solo ione?
Nessuna differenza
di potenziale
Cosa accade alla membrana quando è permeabile ad un solo ione?
Nessuna differenza
di potenziale
Cosa accade alla membrana quando è permeabile ad un solo ione?
Cosa accade alla membrana quando è permeabile ad un solo ione?
Cosa accade alla membrana quando è permeabile ad un solo ione?
Si raggiunge l’equilibrio
elettrochimico:
La forza dovuta al gradiente di
concentrazione eguaglia la
forza dovuta al gradiente
elettrico.
FLUSSO NETTO NULLO.
POTENZIALE DI EQUILIBRIO DELLO IONE
PERMEANTE
La relazione che esiste all’equilibrio tra gradiente chimico e gradiente
elettrico fu stabilita dal chimico-fisico tedesco Walter Nernst:
RT [X]E
E x 
ln
zF [ X] I
Ex= Potenziale di equilibrio per lo ione X;
R= costante dei gas
T= temperatura assoluta (Kelvin)
z= valenza dello ione
F= costante di Faraday (96500 coulomb/grammo
equivalente di carica)
[X]i = Concentrazione intracellulare dello ione X
[X]E= Concentrazione extracellulare dello ione X
L’equazione di Nernst si ricava a partire dalla
considerazione teorica:
WE = WC (all’equilibrio)
WE = zF Ex
WC = RT ln [X]E /[X]I
Quindi:
zF Ex = RT ln [X]E /[X]I
Da qui:
Ex = RT/zF ln[X]E /[X]I
Equazione di Goldman
L’equazione di Goldman permette di descrivere in modo quantitativo
il potenziale di membrana. In definitiva può essere considerata
come una approssimazione dell’equazione di Nernst che tiene conto
della permeabilità della membrana cellulare ai diversi ioni:
RT
Na+e PNa + K+e Pk + Cl-i PCl
Vm =  ln 
zF
Na+e PNa + K+e PK +  Cl-e PCl
-PK ,PNa e PCl sono le costanti di permeabilità delle principali specie ioniche nei
compartimenti intra ed extracellulari.
EQUILIBRIO DI DONNAN
Membrana impermeabile ad una sola delle specie ioniche presenti
to
t1
flusso dovuto al gradiente di concentrazione
flusso dovuto al gradiente elettrico
t2
Quando i flussi unidirezionali contrapposti saranno di
uguale intensità per entrambi gli ioni, il flusso netto
transmembranario delle specie diffusibili sarà nullo e si
avrà:
Vm = EK= ECl
Applicando l’equazione di Nernst si ottiene:
[ K ]1 [Cl ]2

[ K ]2 [Cl ]1
Quindi:
Cl-1K+1=Cl-2K+2
Tale è l’equazione di Donnan dalla quale derivano 2
importanti conseguenze:
1) Ineguale concentrazione degli anioni e dei cationi
diffusibili dal lato della membrana ove si trova la
specie ionica non diffusibile.
Per il principio di elettroneutralità delle soluzioni si
avrà:
K+1=Cl-1
(nel compartimento 1)
K+2=Cl-2 + Pr-2 (nel compartimento 2)
Quindi:
K+2>Cl-2
2) La concentrazione totale degli ioni diffusibili è
maggiore dal lato ove si trova la specie ionica non
diffusibile.
Dall’equazione di Donnan:
Cl-1K+1=Cl-2K+2
Poiché:
Allora:
K+1=Cl-1
K+2>Cl-2
Cl- 2+K+2 >Cl- 1+K+1
Per “effetto Donnan” si produce a cavallo della
membrana:
a) Una differenza di potenziale stabile nel tempo;
b) Un aumento della pressione osmotica del liquido ove
sono presenti
i proteinati.
mantenimento
turgore cellulare
E’ possibile considerare la membrana come un
conduttore ohmico attraverso cui fluiscono
correnti ioniche specifiche. Dato lo ione X,esso
produrrà una corrente avente intensità:
IX = (Vm - EX) gX
Dove gX è la conduttanza della membrana nei
riguardi dello ione X.
Assumendo che in una cellula eccitabile:
Vm= -70 mV
Poiché ECl è quasi uguale a Vm,
ENa= +60 mV
allora si può accettare che il
EK= -84 mV
contributo degli ioni cloruro al
ECl= -72 mV
potenziale di membrana sia nullo.
Alla genesi del potenziale di
membrana partecipano,
dunque, solo sodio e potassio
che sostengono due correnti
ioniche transmembranarie:
Cl-
Pr-
Na+
a) IK diretta dall’interno all’esterno della cellula e
generata dal gradiente di concentrazione.
b) INa diretta dall’esterno all’interno della cellula e
dovuta sia al gradiente di concentrazione,sia al
gradiente elettrico.
All’equilibrio elettrico, che
caratterizza il potenziale di riposo,le
due correnti ioniche saranno di
uguale intensità:
IK =-INa
Per cui la sommatoria delle correnti:
INa + Ik + Icl = 0
Da questa deduzione si ricava la
legge della conduttanza:
Vm= [(gNaENa+gKEk+gClECl)+(INa+IK+ICl)]/(gNa+gK+gCl)
Tale legge permette di predire il potenziale di riposo della membrana
IL RUOLO DELLA POMPA Na+/K+
NELLA GENESI E NEL MENTENIMENTO DEL POTENZIALE
DI MEMBRANA
La pompa Na+/K+ ripristina il
gradiente ionico pompando
attivamente (idrolisi ATP)
3Na+/2K+ rispettivamente
all’esterno e all’interno della
cellula.
La cellula raggiunge lo stato
stazionario quando il Vm sarà
tale che i due flussi attivi
creati dalla pompa sono di
uguale intensità ai flussi
passivi dei due ioni permeanti
attraverso gli appositi
canali(passivi).